旅行时线性插值射线追踪提高计算精度和效率的改进方法

叶 佩，李庆春

1.中国国土资源航空物探遥感中心，北京 100083

2.长安大学地质工程与测绘学院，西安 710054

0 引言

射线理论及射线方法是研究地震波传播理论的重要途径之一，射线理论也经常被用于研究不均匀介质和复杂构造中的地震波传播问题。利用旅行时信息进行层析成像最常用的正演方法就是射线追踪，该方法还被广泛用于偏移、地震波反演及其他正演模拟中，计算地震波的旅行时和波前［1－11］在实际应用中得到了不断的发展与完善。旅行时线性插值（linear travel－time interpolation，LTI）射线追踪法是Asawaka［4］提出来的一种基于线性假设的网格单元扩展方法，该方法已广泛应用于层析成像，具有计算速度快、精度高、易于实现等优点。近年来，国内很多学者对该方法做了大量的研究。如：张建中等［6］推导出了旅行时非线性插值及变速介质中旅行时插值计算公式；为了改善该方法在近场旅行时的精度，降低累计误差，聂建新等［12］提出了旅行时二次／线性联合插值（简称 QLTI）；彭直兴等［13］在震源的近场采用非线性插值计算旅行时，在远场仍用线性插值的计算方法，改善了传统的LTI法因线性插值引起的误差；为了改善旅行时的计算精度和计算效率，孙章庆等［14－15］利用窄带技术来模拟波前，并在局部采用线性插值计算走时，随后，又将该方法扩展到复杂地表走时计算。由于传统的LTI法在进行旅行时计算时射线方向考虑不全，计算的节点旅行时不一定最小，导致追踪的射线路径不一定满足最小旅行时。张东等［16－17］提出在向前处理中采用多方向的循环计算，使所计算的节点旅行时达到最小；同年，又将该方法扩展到三维。梅胜全等［18］用次震源波前面扫描算法代替旅行时插值并通过判定条件进行快速插值的方法来提高计算速度。

Asawaka在文献［4］中指出，LTI算法向前处理过程中计算节点旅行时，应先按列扫描再进行按行扫描，但其并没有对按行扫描进行进一步的分析，也没有给出计算实例说明若不这样做会存在什么样的问题。国内学者在对该算法进行研究时，也没有提到在按列扫描之后还要进行按行扫描，相反让人误以为LTI算法向前处理只需按列扫描即可。但实际上，在向前处理过程中仅按列或按行扫描均没有考虑到逆向传播的射线，在处理速度变化剧烈的介质时，会导致所追踪出来的射线并不满足最小旅行时。因此，笔者通过实例分析，说明LTI算法在向前处理过程中应采用全方位循环扫描的方法，并给出了其具体实现步骤；在保证计算精度的同时，在边界加入次生节点的方法可以大大提高该方法的计算效率。

1 LTI法的基本原理

LTI方法存在一个线性假设前提，如图1所示：设A（xA，zA）、B（xB，zB）两点的坐标已知，A、B 两点的旅行时tA、tB也是已知的，则线段A、B之间任意一点D（xD，zD）的旅行时tD可由A、B两点的旅行时tA、tB线性插值得到，即

其中：tA为旅行时较小的点，即tB≥tA为线段AB长度；r为A到D的距离，满足

图1 LTI法旅行时线性插值几何关系Fig.1 Ttraveltime linear interpolation geometric relationship of LTI method

若射线从A，B之间的D 点穿过到达C点，则C点的旅行时tC可表示为

其中：v为介质的波传播速度；φ为线段AB 与AC之间的夹角。

式（2）中C点的旅行时是关于r的函数。根据最短旅行时原理，射线从D点传到C点应满足

联立公式（2）、（3）可以解出

将式（4）代入式（2）可得C点最小旅行时为

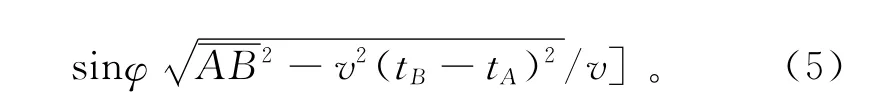
由式（4）可得D点的坐标为

该方法可以分为向前处理和向后处理两步：向前处理是从炮点开始计算炮点到各网格边界节点的最短旅行时，可由式（5）求得；向后处理是从接收点开始，确定所有炮点-接收点的射线路径与各单元网格边界的交点，可由式（6）求得［4，19］。

2 LTI算法存在的问题及其改进

2.1 复杂介质中的逆向传播

LTI算法在向前处理过程中若只按列或按行扫描来计算节点旅行时没有考虑到逆向传播的射线。以按列扫描为例，如图2a所示，S点表示炮点所在位置，R点是其中的一个计算节点，位于炮点右方。LTI算法在向前处理过程中对R点最小旅行时的计算只考虑了炮点S，计算点R所在左半平面的所有射线；而在复杂的速度结构中，射线极有可能先绕到R点的右半平面再传到R点，如图2b所示。同理，当计算点位于炮点左边，也存在同样的问题。这样会导致在横向速度变化剧烈的介质中（即出现逆向传播），计算出来的节点旅行时不是最小，向后处理中追踪出来的射线路径也不满足最短旅行时原理，降低了该方法对复杂模型的适应能力。

图2 逆向传播的射线示意图Fig.2 Schematic illustrations of counterpropagating rays

图3为Asakawa和Kawanaka的一个经典模型［4］，是一个三层速度模型，两低速层中夹有一高速层。模型剖分网格单元大小为0.1m×0.1m。模型参数及观测系统如图3a所示，图3b是只按列扫描LTI算法追踪的初至射线路径，与文献［4］的结果吻合。

图3 Askawa经典模型试验Fig.3 Classic model test of Askawa

为说明射线逆向传播的问题，将图3a的模型及观测系统整体顺时针旋转90°，如图4a所示，重新追踪出的初至波射线路径见图4b。对比图3b，4b中的射线路径可以看出，旋转后追踪的1、2两条射线路径有误。由表1也可以看出，旋转后仅用按列扫描的LTI算法计算出来的1、2两条射线的旅行时不是最小。由图3b中的射线路径可知，正确情况下图4b中标示1、2的2条射线应该是由左侧的高速层折射回来。究其原因是只按列扫描的LTI法在向前处理过程中，计算震源左侧单元节点最小旅行时只考虑了来自右半平面的射线，并没有考虑来自左半平面的射线。同理，只按行扫描也存在射线考虑不全的问题。因此，笔者认为只按列或按行扫描的LTI法在向前处理过程并没有考虑来自各个方向的射线，只有采用全方位循环的方法才能确保计算得到的各节点的旅行时满足最小。

图4 LTI法向前处理按列扫描及其缺陷Fig.4 Forward processing by column scanning and its defects of LTI method

表1 Asakawa模型旋转前后旅行时计算比较Table1 Traveltime comparison of Asakawa’s model calculated before and after rotation

在具体实施中，先按LTI算法按列扫描计算各节点的旅行时，再按行扫描的方法来重新计算各网格节点旅行时；将按行扫描计算的节点旅行时与按列扫描计算的节点旅行时相比较，取其中旅行时最小的值作为网格节点的旅行时。这样就可以确保在向前处理过程中考虑来自各个方向的射线，即所计算出来的节点旅行时是最小的。

全方位循环法向前处理实现步骤如下。

1）先用LTI算法按列扫描计算出整个区域各网格节点的旅行时［4］。

2）除震源所在网格外，重新计算震源所在行各节点的旅行时（按行扫描），如图5a所示，并与原先按列扫描计算的结果对比，取其中最小值作为节点的旅行时。

3）由下到上逐个计算震源所在行上面所有节点的旅行时：

①计算各单元水平边界及垂直边界上各节点的旅行时，这时只考虑来自下边界的射线（图5b），并与原先按列计算的比较，取其中旅行时最小的；

②从左往右，利用单元左边界上的已知点计算右边界和上边界节点的旅行时（图5c），并与节点已有值比较，取其中旅行时最小的；

③从右往左，利用单元右边界上的已知点计算左边界和上边界节点的旅行时（图5d），并与节点已有值比较，取其中旅行时最小的。

通过①、②、③步计算，就可求得震源所在行上面所有节点的最小旅行时。

4）同理，从上到下可以计算出震源所在行下面各节点的旅行时，并与按列计算的旅行时比较取其中最小的。最后可得到整个模型区域内所有节点的最小旅行时。

图6为LTI算法全方位循环对图4a追踪的结果。与图3b相比，追踪的射线其路径和理论值是一样的，尤其是标示为1、2的两条射线，其旅行时与理论值一致（表1）。由试算结果可知，LTI算法全方位循环法在向前处理过程中可以确保计算出来的节点旅行时最小，从而能够避免仅按列或按行扫描未考虑逆向传播的射线导致在横向变化剧烈的模型中所追踪出来的初至射线路径不满足最小旅行时原理的问题。

2.2 LTI算法的计算效率

LTI法是基于线性假设的，模型网格剖分的精细程度直接影响射线旅行时的计算精度：在一定范围内，网格剖分越精细，射线旅行时精度越高；但网格剖分得越精细，在计算时，所耗费的时间也就越长。因此在保证计算精度同时，如何提高计算效率也是目前需解决的问题。

为了保证LTI法的计算精度，同时提高该方法的计算效率，笔者提出在网格单元边界加入次生节点的技巧。

图5 向前处理按行扫描计算节点最小旅行时的实现过程Fig.5 Implementation process of minimum travel－time of grid node calculated by line scanning in the forward processing

图6 LTI算法全方位循环法模型射线追踪路径结果图Fig.6 Ray traces calculated by all－round cycling of LTI method

图7a是改进前LTI算法网格节点示意图，图7b为改进后在网格边界插入次生节点的示意图。可以看出，在剖分精度相同的情况下，传统LTI计算点数多。改进后只在主节点上给定速度值，边界上插入的次生节点速度可由单元边界上相邻两主节点的速度线性插值得到；而原来的做法（图7a）则需在每个节点都赋速度值。因此在将该方法用于层析成像时，插入次生节点的LTI法在不影响计算精度的前提下所需反演的参数更少，更有利于反演。

为了验证加入次生节点后LTI法的计算精度，建立一均匀速度模型。模型参数及观测系统如图8a所示。图8b显示的是网格剖分个数为10×10，单元边界次生节点数为99×99，即节点间距为1m情况下的初至波射线路径；表2列出了传统的LTI法与网格边界插入次生节点的LTI法在节点间距为5m和1m两种情况下各道所接收到的初至波旅行时；图9给出了不同节点间距下插入次生节点前后LTI法的计算耗时。

图7 网格边界插入次生节点前（a）后（b）布置示意图Fig.7 Schematic illustrations of before（a）and after（b）secondary node inserted into mesh boundary

由表2可以看出：在节点间距为5m的情况下，传统的LTI法绝对误差最大值为0.391ms，在单元边界插入次生节点后其绝对误差最大值降为0.006 ms；在节点间距为1m的情况下，传统的LTI法绝对误差最大值为0.084ms，单元边界插入次生节点后绝对误差最大值为0ms。从图9中可以看到在节点间距相同的情况下，传统的LTI法比插入次生节点的LTI法耗时少，而且随着节点间距逐渐减小，耗时的下降更为显著。从试算结果可以看到：在节点间距相同的情况下，网格边界插入次生节点的LTI法较传统的LTI法计算精度至少可以提高一个数量级。同时，计算速度也更快，随着节点间距剖分的越精细，计算耗时下降也越明显，计算速度较传统的方法可提高n倍。

图8 网格边界插入次生节点模型试验Fig.8 Model test of secondary node inserted into grid boundary

3 复杂模型测试

为了综合检验改进后LTI法对复杂模型的适应能力，笔者引用了经典的Marmousi模型对改进前后的LTI法进行试算及误差分析。

图9 不同节点间距下插入次生节点前后LTI法CPU耗时Fig.9 CPU time of LTI method before and after secondary nodes inserted into grid boundary with different node spacing

图10为Marmousi模型的试算结果。模型参数为：网格数384×122，网格大小10m×10m，速度位于网格节点。观测系统设置参数：激发点位于模型底部（2 800，1 220），在模型顶部均匀放置77个接收点，接收点分别位于：（0，0），（50，0），（100，0），…，（3 800，0）。图10是改进后的LTI算法追踪出来的初至射线路径，次生节点数为4×4。由射线路径可以看出，在模型底部，射线沿着高速层走，符合最小旅行时射线路径的规律。图11是传统的LTI法计算的各道初至旅行时减去改进后的LTI法计算的各道初至旅行时得到的旅行时残差曲线。可以看到，所计算出来的旅行时残差均处于残差为0的参考线上方，也就是说改进后的LTI算法算出来的初至旅行时小于传统的LTI法所计算出来的初至旅行时。可以验证改进后的LTI算法较传统的LTI法计算精度更高，且改进后的LTI法对复杂模型具有更强的适应能力及稳定性。

图10 Marmousi模型改进LTI法初至射线路径示意图（★.激发点）Fig.10 Schematic illustrations of Marmousi model firstbreak races calculated by improved LTI method

表2 网格边界插入次生节点LTI法与传统LTI法初至波旅行时计算结果对比Table2 First－break traveltime comparison of traditional LTI and second node inserted into grid boundary LTI ms

图11 传统LTI法与改进后LTI法追踪的旅行时残差示意图Fig.11 Schematic illustrations of traveltime residuals between traditional and improved LTI

4 结论

1）笔者用实例详细分析了LTI算法仅按列或按行扫描没有考虑到逆向传播的射线，因此建议在向前处理时采用全方位循环的方法计算网格节点走时，这样可以确保追踪出来的射线路径满足最短旅行时。

2）在保证计算精度的前提下，为能有效地提高计算效率，笔者采用在网格边界加入次生节点的措施。试算结果表明，较传统的LTI法，本文所采用的LTI算法其适应能力更强、计算精度及计算效率均大幅度提高。

3）本文采用2D模型，由于其高精度、高效率的特点，稍加扩展后即可较好地适用三维射线追踪及三维层析成像。

（References）：

［1］Vidale J E.Finite Difference Calculation of Traveltimes［J］.Bulletin of the Seismological Society of America，1988，78（6）：2062－2076.

［2］Vidale J E.Finite Difference Calculation of Traveltime in Three Dimensions［J］.Geophysics，1990，55（5）：521－526.

［3］Moser T J.Shortest Path Calculation of Seismic Rays［J］.Geophysics，1991，56：59－67.

［4］Asawaka E，Kawanaka T.Seismic Ray Tracing Using Linear Traveltime Interpolation ［J］. Geophysical Prospecting，1993，41：99－111.

［5］Sethian J A.A Fast Marching Level Set Method for Monotonically Advancing Fronts［J］.Proe Nat Acad Sci，1996，93（4）：1591－1595.

［6］张建中，陈世军.复杂介质地震初至波数值模型［J］.计算物理，2003，20（5）：429－433.Zhang Jianzhong，Chen Shijun.Numerical Modeling of Seismic First－Break in Complex Media［J］.Chinese Journal of Computational Physics，2003，20（5）：429－433.

［7］唐小平，白超英.最短路径算法下三维层状介质中多次波追踪［J］.地球物理学报，2009，52（10）：2635－2643.Tang Xiaoping，Bai Chaoying.Multiple Ray Tracing Within 3－D Layered Media with the Shortest Path Method［J］.Chinese J Geophys，2009，52（10）：2635－2643.

［8］孙章庆，孙建国，韩复兴.复杂地表条件下快速推进法地震波走时计算［J］.计算物理，2010，27（2）：281－286.Sun Zhangqing，Sun Jianguo，Han Fuxing.Traveltime Computation Using Fast Marching Method Under Complex Topographical Conditions ［J］. Chinese Journal of Computational Physics，2010，27（2）：281－286.

［9］孙章庆，孙建国，韩复兴.针对复杂地形的三种地震波走时算法及对比［J］.地球物理学报，2012，55（2）：560－568.Sun Zhangqing，Sun Jianguo，Han Fuxing.The Comparison of Three Schemes for Computing Seismic Wave Traveltimes in Complex Topographical Conditions［J］.Chinese J Geophys，2012，55（2）：560－568.

［10］韩复兴，孙建国，杨昊.基于二维三次卷积插值算法的波前构建射线追踪［J］.吉林大学学报：地球科学版，2008，38（2）：336－340.Han Fuxing，Sun Jianguo，Yang Hao.Ray－Tracing of Wavefront Construction by Bicubic Convolution Interpolation［J］.Journal of Jilin University：Earth Science Edition，2008，38（2）：336－340.

［11］赵昭，赵志新，徐纪人，等.高精度人工地震波层析成像技术勘探地下构造［J］.吉林大学学报：地球科学版，2011，41（1）：362－367.Zhao Zhao，Zhao Zhixin，Xu Jiren，et al.Surveying Structures with High－Resolution Explosion Seismic Tomography［J］.Journal of Jilin University：Earth Science Edition，2011，41（1）：362－367.

［12］聂建新，杨慧珠.地震波旅行时二次／线性联合插值法［J］.清华大学学报：自然科学版，2003，43（11）：1495－1498.Nie Jianxin，Yang Huizhu.Quadratic／Linear Travel－Time Interpolation of Seismic Ray Tracing［J］.J Tsinghua Univ：Sci ＆ Tech，2003，43（11）：1495－1498.

［13］彭直兴，张芬，周熙襄，等.地震波旅行时非线性／线性联合插值法［J］.成都理工大学学报：自然科学版，2005，32（3）：322－324.Peng Zhixing，Zhang Fen，Zhou Xixiang，et al.Nonlinear／Linear Interpolation of Seismic Traveltime［J］.Journal of Chengdu University of Techonlogy：Science ＆ Technology Edition，2005，32（3）：322－324.

［14］孙章庆，孙建国，韩复兴.复杂地表条件下基于线性插值和窄带技术的地震波走时计算［J］.地球物理学报，2009，52（11）：2846－2853.Sun Zhangqing， Sun Jianguo， Han Fuxing.Traveltimes Computation Using Linear Interpolation and Narrow Band Technique Under Complex Topographical Conditions［J］.Chinese J Geophys，2009，52（11）：2846－2853.

［15］孙章庆，孙建国，韩复兴.基于线性插值和窄带技术的走时计算方法［J］.石油地球物理勘探，2009，44（4）：436－441.Sun Zhangqing， Sun Jianguo， Han Fuxing.Traveltime Computation Based on Linear Interpolation and Narrow Band Technique［J］.Oil Geophysical Prospecting，2009，44（4）：436－441.

［16］张东，谢宝莲，杨艳，等.一种改进的线性旅行时插值射线追踪算法［J］.地球物理学报，2009，52（1）：200－205.Zhang Dong，Xie Baolian，Yang Yan，et al.A Ray Tracing Method Based on Improved Linear Travel－Time Interpolation［J］.Chinese J Geophys，2009，52（1）：200－205.

［17］张东，傅相如，杨艳，等.基于LTI和网格界面剖分的三维地震射线追踪算法［J］.地球物理学报，2009，52（9）：2370－2376.Zhang Dong，Fu Xiangru，Yang Yan，et al.3－D Seismic Ray Tracing Algorithm Based on LTI and Partition of Grid Interface［J］.Chinese J Geophys，2009，52（9）：2370－2376.

［18］梅胜全，邓飞，钟本善，等.基于改进的双线性旅行时插值的三维射线追踪［J］.物探化探计算技术，2010，32（2）：152－156.Mei Shengquan，Deng Fei，Zhong Benshan，et al.3－D Ray Tracing Based on Improved Bilinear Travel－Time Interpolation ［J］. Geophysical ＆ Geochemical Computing Technique，2010，32（2）：152－156.

［19］叶佩，李庆春.旅行时线性插值射线追踪及提高计算精度和效率的改进措施［C］／／中国地球物理学会年会.长沙：中国科学技术大学出版社，2011：757.Ye Pei，Li Qingchun.Improvements of Linear Traveltime Interpolation Ray Tracing for the Accuracy and Effiency ［C］／／Annual Meeting of Chinese Geophysical Society. Changsha： China Science and Technology University Press，2011：757.