梯度反褶积法及其在矿产勘探中的应用

马国庆，杜晓娟，李丽丽，李文成，王凤刚

1.吉林大学地球探测科学与技术学院，长春 130026

2.首钢地质勘查院地质研究所，北京 100144

0 引言

重磁异常的梯度信息能更好地描述地下地质体的细节特征，在近几年应用十分广泛，国内外已经陆续开展重磁梯度测量。欧拉反褶积法是一种常用的位场自动解释方法［1－2］，人们通过对常规欧拉反褶积公式求导实现了梯度数据的解释［3－5］，获得了较好的实际应用效果，但是该方法仍需要构造指数参与计算。由于在实际数据解释中测区内地质体的类型是未知的，构造指数无法准确地获得，且构造指数的微小误差会使反演结果产生较大的影响［6－8］，笔者提出梯度反褶积法完成梯度数据的反演。

梯度反褶积法是在常规欧拉反褶积法的基础上推导出来的，且在公式中消去了构造指数，避免了因构造指数选取不当造成的误差，使反演结果更加准确。通过理论模型证明梯度反褶积法在位场梯度反演中的有效性，且相对常规欧拉反褶积法其精度较高，适用性更强。将本方法应用于某铁矿区的实测磁梯度数据，确定了铁矿的赋存状态。

1 梯度反褶积法

梯度反褶积法以梯度数据为基础进行场源体的反演，是在欧拉反褶积法基础上推导出来的。常规欧拉反褶积法［9－10］的公式为

其中：T表示重力异常或磁异常；（x0，z0）分别表示异常体的埋藏位置；N为地质体的构造指数；B表示背景异常场。为了使式（1）可适用于梯度数据，分别计算其在x，z方向的导数：

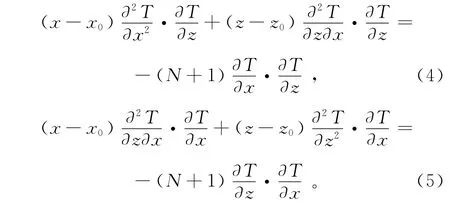
对比发现，式（4）与式（5）右侧相等，因此左侧也相等，因此可以得到

利用式（7）通过重磁梯度异常可以获得异常体的位置信息（x0，z0）。

从式（7）中可以看出，梯度反褶积公式完成了梯度数据的反演，并且去除了构造指数的影响。

同理，可以推导出三维情况下梯度反褶积法的表达式：

2 理论模型试验

直角坐标系下，存在水平位置为（55m，55m）、埋深为50m、半径为7m的球体，当计算点距为1 m时引起的梯度异常如图1所示。为了试验梯度反褶积法的应用效果，分别利用常规欧拉反褶积法和梯度反褶积法对梯度异常进行反演，反演结果如图2所示。

从图2a、b中可以看出，常规欧拉反褶积法和梯度欧拉反褶积法均能很好地给出异常体的真实水平位置。图2c和图2d分别为利用这2种方法计算得到的深度统计结果，可以看出，2种方法均能很准确地完成异常体深度的反演，但梯度欧拉反褶积法得到的结果发散程度较小，且误差小于5%。

为了试验方法的稳定性，将计算点距加大到5 m。因为球体的半径为7m，因此在其正上方仅存在4个点。在点数比较少的情况下反演结果的准确度会降低。分别利用常规欧拉反褶积法和梯度反褶积法对球体引起的异常进行反演，反演结果如图3所示。从图3中可以看出：常规欧拉反褶积法在计算点距较大的情况下，反演得到的异常体的水平位置分散，无法准确给出场源体的位置信息，其结果与理论值之间偏差较大；梯度反褶积法仍能较好完成异常的反演，能很好地描述地质体的真实位置。

图1 球体引起的重力异常及梯度异常Fig.1 Gravity and gradient anomaly of sphere

图2 球体重力异常反演结果Fig.2 Inversion results of gravity anomaly caused by sphere

图3 球体重力异常反演结果Fig.3 Inversion results of gravity anomaly caused by sphere

下面试验一下2种方法存在多个异常体时的情况。在水平位置（35m，35m）和（65m，65m）处存在埋深均为15m的球体，并在引起的重力异常中加入均值为0、方差为1mGal的高斯噪声。其原始重力异常及其梯度异常如图4所示。

分别利用常规欧拉反褶积法和梯度欧拉反褶积法对图4中所示异常进行反演，结果如图5所示。

图4 球体引起的重力异常及梯度异常Fig.4 Gravity and gradient anomaly of sphere

图5 球体重力异常的反演结果Fig.5 Inversion results of gravity anomaly caused by sphere

从图5的反演结果中可以看出：由于噪声的影响，常规欧拉反褶积法的反演结果在异常周围产生了一定的干扰，即产生多余的干扰异常，为解释带来困难；梯度反褶积法的反演结果受噪声干扰较小，所得到的结果能较好地反映异常体的位置和深度。为了试验梯度反褶积法对不同形状地质体的应用效果，采用了上顶埋深为10m、边长为20m的正方体，其引起的原始重力及其梯度异常如图6所示。

分别利用常规欧拉反褶积法和梯度反褶积法对正方体进行反演，在利用常规欧拉反褶积进行反演时构造指数选取0，2种方法的反演结果如图7所示。

图6 正方体引起的重力异常及梯度异常Fig.6 Gravity and gradient anomaly caused by square

图7 正方体引起异常的反演结果Fig.7 Inversion results of gravity anomaly caused by square

从图7可以看出：常规欧拉反褶积法难以确定异常体的水平位置，且深度与理论值之间也存在一定的误差；梯度反褶积法能很好地圈定异常体的范围，且反演得到的深度与理论值一致，其均值与理论值之间的误差小于5%。

通过上述试验可以看出，梯度反褶积法反演结果的精度明显优于常规欧拉反褶积法的反演结果，能更加有效地完成位场异常的反演，且适用性较强。

3 实际数据应用

应用梯度反褶积法解释实际航磁梯度数据。图8为河北迁安地区实测航磁及梯度异常。迁安地区主要发育沉积变质型铁矿，经过50多年的开采，地形地貌遭到严重破坏，磁异常形态已经发生很大改变。磁梯度测量具有不受外界环境及日变的干扰，数据更加稳定，因此采用磁梯度异常来确定地下铁矿的分布特征，为下一步开采提供基础性依据。本次航磁梯度测量的总误差为0.002 1nT／m，分别利用常规欧拉反褶积法和梯度反褶积法对该地区数据进行反演。根据异常的形态特征，在利用常规欧拉反褶积进行反演时构造指数选取1，反演结果如图9所示。

从图9可以看出：常规欧拉反褶积法的结果较发散，对于详查测线的布设及井口的布设不能提供强有力的支持；梯度反褶积法计算结果明显优于常规欧拉反褶积结果，该方法的结果比较集中，离散点比较少，能较准确地给出铁矿的分布范围，为开采计划提供明确的方向。

4 结论

图8 铁矿区航磁异常及梯度异常Fig.8 Aeromagnetic and gradient anomaly of an iron ore area

1）笔者提出的位场反演方法——梯度反褶积法，以欧拉反褶积法为基础，通过求导被推广到梯度数据处理中，并在反演公式中消去了构造指数，避免了构造指数选取不当给反演结果带来的误差 。

2）通过模型试验，验证了梯度反褶积法在位场反演中的有效性，其反演精度高于常规欧拉反褶积法。

3）梯度反褶积法对铁矿区实测异常的反演结果集中、离散点少，能较准确地给出铁矿的分布范围，为下一步开采计划提供基础性依据。

图9 铁矿区磁异常反演结果Fig.9 Inversion results of aeromagnetic anomaly in the iron ore area

黄大年教授在论文修改过程中提出了宝贵意见，工作组的同仁们为本文提供了宝贵的资料，在此一并致谢。

（References）：

［1］马国庆，孟令顺，李丽丽.龙门山及邻区断裂分布及地震前后断裂形态差异［J］.吉林大学学报：地球科学版，2012，42（2）：519－525.Ma Guoqing，Meng Lingshun，Li Lili.Fault Distribution of Longmenshan and Adjacent Regions and Fault Morphological Differences Before and After Earthquake［J］.Journal of Jilin University：Earth Science E－dition，2012，42（2）：519－525.

［2］李丽丽，杜晓娟，马国庆.改进的局部波数法及其在磁场数据解释中的应用［J］.吉林大学学报：地球科学版，2012，42（4）：1179－1185.Li Lili，Du Xiaojuan，Ma Guoqing.Improved Local Wavenumber Methods in the Interpretation of Magnetic Fields［J］.Journal of Jilin University：Earth Science Edition，2012，42（4）：1179－1185.

［3］Huang D，Gubbins D，Clark R A，et al.Combined Study of Euler’s Homogeneity Equation for Gravity and Magnetic Field［C］／／57th EAGE Conference.Glasgow：European Association of Geoscientists and Engineers，1995：144.

［4］Salem A，Ravat D，Mushayandebvu M F，et al.Linearized Least Squares Method for Interpretation of Potential－Field Data from Sources of Simple Geometry［J］.Geophysics，2004，69（3）：783－788.

［5］Schimidt P W，Clark A.The Magnetic Gradient Tensor：Its Properties and Uses in Source Characterization［J］.The Leading Edge，2006，25（1）：75－78.

［6］Barbosa V C F，Silva J B C，Medeiros W E.Stability Analysis and Improvement of Structural Index Estimation in Euler Deconvolution［J］.Geophysics，1999，64（1）：48－60.

［7］Daniela G，Marcos J，Arauzo B.Automatic Interpretation of Magnetic Data Based on Euler Deconvolution with Unprescribed Structural Index［J］.Computers ＆Geosciences，2003，29（8）：949－960.

［8］Hansen R O，Laura S.Multiple－Source Euler Deconvolution［J］.Geophysics，2002，67（2）：525－535.

［9］Thompson D T.‘EULDPH’：A New Technique for Making Computer－Assisted Depth Estimates from Magnetic Data［J］.Geophysics，1982，47（1）：31－37.

［10］Reid A B，Allsop J M，Granser H，et al.Magnetic Interpretation in Three Dimensions Using Euler Deconvolution［J］.Geophysics，1990，55（1）：80－91.