电动车用永磁同步电动机FOC控制系统实现

，，

（重庆邮电大学自动化学院，重庆 400065）

1 引言

电动机控制技术是电动车驱动系统的核心技术之一［1］。目前，应用在电动车上的电动机主要有感应电机、直流无刷电机、开关磁阻电机和永磁同步电机等。随着永磁体技术和电力电子技术的不断发展及其自身固有的效率高、惯性小、高转矩密度和易于控制等优点［2］，永磁同步电动机在电动车领域得到了越来越广泛的应用［3-5］。

永磁同步电动机和感应电动机结构相似，是一个非线性多变量耦合系统，永磁同步电动机控制是一个复杂的工程问题。矢量控制技术的发展使永磁同步电动机获得了与直流电动机相同的控制效果。目前，应用于电动车电机驱动的矢量控制法主要有磁场定向控制（FOC）和直接转矩控制（direct torque control，DTC）。

FOC的基本思想是通过矢量变换将永磁同步电动机的定子电流分解到转子同步旋转的坐标系中，对励磁电流分量（d轴分量）和转矩电流分量（q轴分量）分别加以控制，从而使永磁同步电动机具有与直流电动机相同的控制特性。该控制技术的主要优点是动态响应速度快、转矩波动小［6］。主要缺点是定子电阻等电机参数会对控制算法产生影响，但是很多文章已经提出了解决这种参数变化而对控制效果产生干扰的方法［7-8］。目前，对FOC的研究主要集中在两个方面：一方面控制系统响应的快速性和准确性；另一方面减小控制算法的复杂度［8］。

相较于FOC控制，DTC控制虽然具有更好的瞬态响应、受电动机参数变化影响小等优点，但是其自身也存在着诸多缺点：启动和低速运转困难，电流和转矩波动大等［9］。从稳定性和安全性角度考虑，其在电动车牵引方面的应用并不是特别广泛。目前，在动力牵引方面，FOC控制仍然是优先选择的永磁同步电动机的控制策略［10-11］。

本文在分析永磁同步电动机FOC控制算法的基础上建立了永磁同步电动机的数学模型，并设计了一套永磁同步电动机控制系统的软硬件系统，最后建立了一套实验系统对所设计的系统进行实际测试。

2 永磁同步电动机数学模型

2.1 永磁同步电动机坐标系

永磁同步电动机的FOC控制一般使用3个坐标系进行描述，如图1所示［12-13］。

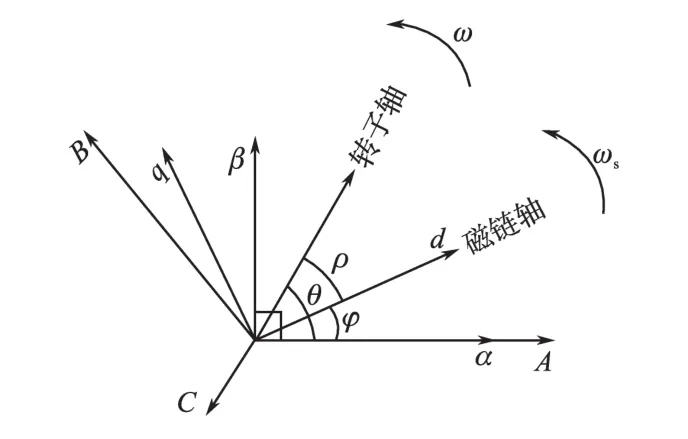
图1 描述永磁同步电动机的3个坐标系Fig.1 The three coordinate system of PMSM

图1中ABC是三相定子坐标系、α，β是两相静止坐标系，d,q是旋转坐标系。ABC三相定子坐标系又称为同步电机自然坐标系，其坐标轴A，B，C的位置分别为电机定子三相绕组U，V，W的轴线方向，在空间上互差120°的电角度。α，β两相静止坐标系是固定在电机定子上的坐标系，其中α向量与A轴重合，β向量正交于α向量。dq旋转坐标系是固定在转子磁链上的坐标系，其中d向量与转子磁链的合成向量重合，q向量正交于d向量。dq旋转坐标系与转子磁链同步旋转。id为方向电流，用以表征永磁同步电动机的转子磁场；iq为正交电流，用以表征永磁同步电动机对外输出的机械转矩。

图1中，θ为旋转角；ω为转子机械转速；φ为转子磁链角，φ=θ+ρ；ωs为同步转速；ρ为转差角。

2.2 dq旋转坐标系下的数学模型

永磁同步电动机运动方程一般是建立在dq旋转坐标系下的。为了建立dq旋转坐标系，首先假设［13-14］：1）永磁体产生恒定磁场，磁场变化为零；2）忽略铁心饱和；3）不计电动机中的涡流和磁滞损耗；4）电动机的电流为三相对称正弦电流；5）定子绕组感应反向电动势为正弦电压；6）转子上无阻尼绕组。

在以上假设条件下，dq旋转坐标系下的机械运动方程为

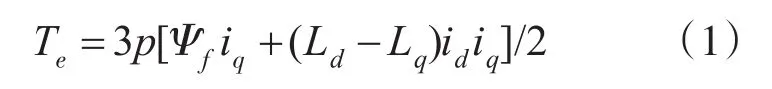
式中：Ld，Lq分别为d，q轴电感；Ψf为由转子永磁体产生的恒定磁链；p为磁极对数。

在表面式永磁同步电动机中，由于Ld=Lq，式（1）可简化为

由式（2）可以看出，表面永磁同步电动机的电磁转矩与q轴电流成正比例关系，通过q轴电流就能够控制电磁转矩的大小，得到与直流电机相同的控制特性。在内置式永磁同步电动机中，由于Ld≠Lq，不能做上述的简化。但是，如果采用id=0的控制方式，便可得到如式（2）的简化效果，从而使电机得到相同的控制效果。

3 永磁同步电动机的FOC控制

FOC控制主要由5个部分组成：PI控制器、Clarke变换、Park变换及Park逆变换和SVPWM单元，如图2所示。

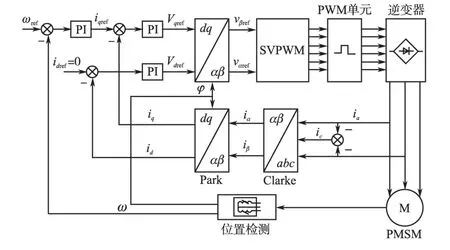
图2 FOC控制原理图Fig.2 The control principle of FOC

图2中，3个PI控制器的作用各有不同，它们分别用于速度环和电流环的调节。由电流传感器测得的电流处于ABC三相静止坐标系下，该值要通过Clarke变换和Park变换转换到dq旋转坐标系中，得到在dq坐标系下的电流值id和iq。永磁同步电动机的实际转速ω和转子位置角φ由位置传感器测得。在本系统采用旋转编码器作为位置传感器。当ω和给定转速ωref不同时，速度环PI控制就会根据偏差调节q轴给定电流iqref的大小，从而控制电动机电磁转矩的输出。为了能够达到与直流电动机相同的控制效果，采用id=0控制。通过iqref来控制电动机电磁转矩大小。在dq旋转坐标系下，id与idref和iq与iqref的偏差值分别通过d，q轴PI控制器的调节得到d，q轴的给定电压vdref和vqref。最后通过Park逆变换将vdref和vqref转换到两相静止坐标系下的电压vαref和vβref。两者作为SVPWM单元的基准电压，用于计算每路输出电压的占空比。

4 PMSM控制系统设计

4.1 系统硬件设计

本文所设计的永磁同步电动机控制系统结构如图3所示。该系统主要由稳压直流电源、电机控制器、计算机和永磁同步电动机4部分组成。

图3 永磁同步电动机控制系统硬件框图Fig.3 The hardware block diagram of PMSM control system

为了保证电动机控制系统运行的稳定，用直流稳压电源代替车载动力电池作为电动机的动力电源。计算机用以向电动机控制器发送控制命令，两者之间的通信由RS232完成。电动机控制器由逻辑电路、驱动电路、IGBT单元、母线电容和水冷槽组成。除了控制芯片外，逻辑电路的其他功能模块包括：电源模块、信号调理电路、通信收发电路以及位置传感器电路等。采用IGBT集成单元作为功率逆变器。如果电动机需要长时间运行，要将水冷槽与循环水箱连接，用来为电动机控制器的散热。直流母线电容能够滤除电网中的谐波，保持直流电压稳定，为逆变器提供低阻抗电压源。采用LEM电流传感器采集三相定子电流，转子速度和位置信号的采集用旋转编码器来完成。

4.2 电流信号处理电路设计

电流信号处理电路由电流采集部分和信号处理部分组成。电流采集部分采用LEM HC5F300-S传感器。

该传感器采用+5 V单电源供电，相对而言较易实现。被测电流与传感器输出电压的关系为

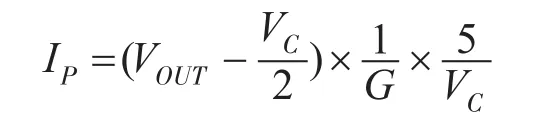
式中：IP为被测电流；VOUT为输出电压；VC为供电电压；G为灵敏度。

通过A/D转换器将VOUT的值读取到运算器中，便可获取当前的被测电流值。前两相电流ia,ib由电流传感器测得，第3相电流值通过关系式ia+ib+ic=0计算得到，可以减少硬件成本。

为了降低噪声干扰，在VOUT进行A/D转换之前，要进行滤波处理。为了有效滤除三相定子电流中的谐波成分，采用二阶低通有源滤波电路。电路图如图4所示。

图4 二阶低通有源滤波电路Fig.4 The active filter circuit with second-order low-pass function

4.3 转子位置采集电路设计

与绝对式光栅编码器、霍耳传感器相比，旋转编码器具有高精度、结构可靠、实用性好、环境适应能力强等优点，适用于电动车工作时的温度、湿度变化大，机械振动强度高等复杂工况环境下。旋转编码器的原理图如图5所示。它的基本原理是：在R1-R2端加入激励信号Vr=后，在 S1-S3和 S2-S4端分别得到Va=与位置角有关的响应信号，通过对Va和Vb进行解调，就可以得到当前转子位置角。

图5 磁阻式旋转编码器Fig.5 Reluctive resolver to digital converter

为了增强系统的集成度和减少控制运算器的工作负荷，采用AD2S1200集成芯片对旋转编码器信号进行预处理。利用该芯片可直接得出转子位置角，通过SSC发送到控制运算器中。R1-R2端激励信号的频率为10 kHz，幅值为2.5 V。

5 软件设计

5.1 软件框架设计

在软件方面，为了方便今后程序的移植和完善，FOC控制程序采用层次化的编程方式，如图6所示。

图6 FOC程序软件框架Fig.6 FOC software framework

电动机控制程序整体上分成两个部分：可视化的上位机操作界面和基于数字控制器的电动机驱动程序。两者之间通过RS232串口通讯实现人机交互。在实验过程中，可以通过向控制器发送自定义的人机交互指令来实现电动机的不同运行状态，如启动、调速、停止等。这些交互指令也包含电动机的不同控制模式，如：开环控制、闭环控制以及转矩控制等。选择什么样的控制模式，要根据具体的实验情况而定。

5.2 PI控制器设计

永磁同步电动机的控制系统是一个双闭环控制系统：电流环和速度环。为了方便说明问题，将双闭环结构拆解开来研究。其中，电流环闭环结构如图7所示。

图7 电流环闭环结构图Fig.7 The closed loop structure of current loop

图7中电流环控制对象的传递函数为

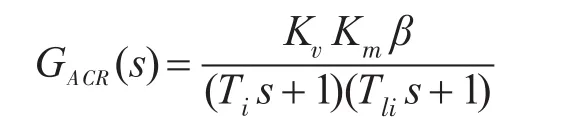
式中：GACR为电流环调节器传递函数；KV为逆变器放大倍数，定义为逆变器输出电压与电流调节器输出电压之比；Km=1/Rs；Tli=Lq/Rs；Ti为逆变器最小惯性环节时间常数；β为电流反馈系数。

考虑到电流环一般以其跟踪性能要求为主，对电网电压的抗干扰作用是次要因素，按照调节器工程设计方法，将电流环校正成典型Ⅰ型系统，GACR选为PI控制器：

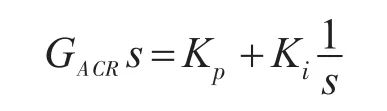
上述PI控制器的离散化表示形式为

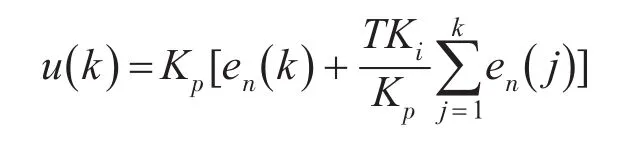
为了DSP计算的方便性，采用增量式数字PI算法：

通过上面的整定后，电流环的等效传递函数为

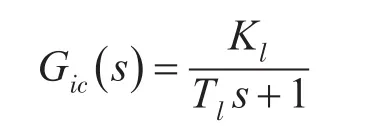
式中

速度环的等效结构如图8所示。

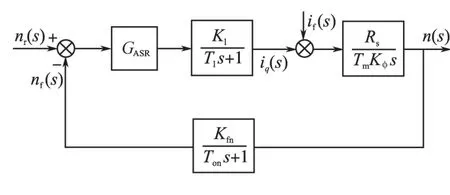
图8 速度环闭环结构图Fig.8 The closed loop structure of speed loop

图8中，Kfn为速度反馈系数，Kφ为电机电势系数，Tm为电机机电时间常数，Ton为速度反馈滤波时间常数。

按照以上分析方法，在速度环加入PI控制器后，可校正成典型的Ⅱ型系统，开环可在实现速度响应无静差的同时，满足动态抗干扰性能好的要求。

校正后，速度环的开环传递函数为

6 实验及结果分析

在进行上述理论分析和控制系统设计的基础上，本文根据图3的结构搭建了相应实验测试平台进行验证。系统采用1台额定功率为10 kW的永磁同步电动机作为实验电机。该电动机的其他主要参数包括：极对数为6对，额定电压为109～190 V，定子电阻为0.4 Ω，定子电感为1.55 mH。

同时，系统使用一个可调直流稳压电源来模拟电动车的车载动力电池。并在测试过程中，利用示波器、横河功率分析仪来观察和记载转速、电流波形。

实验过程中，通过人机交互界面对PI控制器各参数做如下设置：速度环Kp=25，Ki=20；电流环id，Kp=0.018，Ki=25；电流环iq，Kp=0.018，Ki=25。

设置目标转速为300 r/min，得到的实测响应曲线如图9所示。由该响应曲线图可以看出，系统具有良好的启动效果，能够快速准确地达到设定的目标转速。

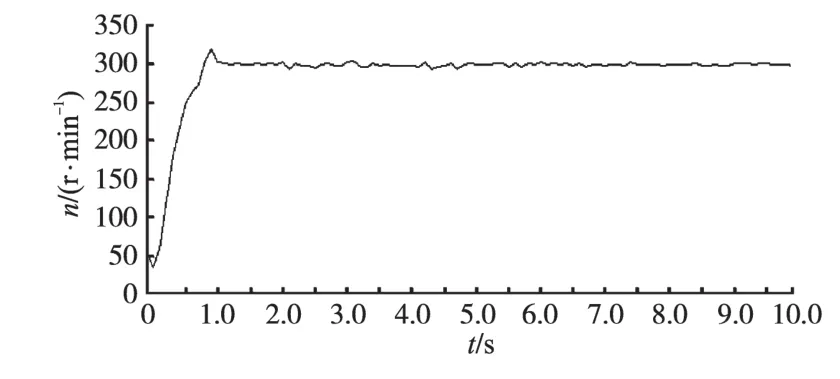
图9 转速为300 r/min的实测曲线Fig.9 The measured curve with rotate speed 300 r/min

待电动机启动稳定后，将电机加速到1 000 r/min；在此转速基础上，调节电动机的转速分别至1 500 r/min和500 r/min，得到图10、图11所示的响应曲线图。从该响应曲线可以看出系统具有良好的速度调节能力。

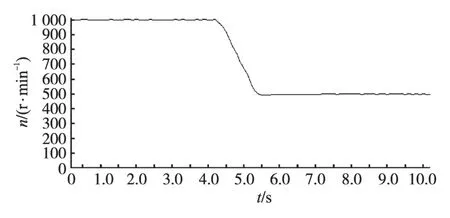
图10 转速由1 000 r/min加速到1 500 r/min的实测曲线Fig.10 The measured curve with rotate speed 1 000 r/min increasing to 1 500 r/min

图11 转速由1 000 r/min减速到500 r/min的实测曲线Fig.11 The measured curve with rotate speed 1 000 r/min minimizing to 500 r/min

7 结论

本文提出了一种基于FOC的电动车永磁同步电动机控制算法的系统方案，并进行了理论分析及硬件系统和软件系统的设计，并通过实验证明该控制系统能够安全可靠地实现永磁同步电动机的开、闭环控制。

由于电动车存储能量有限，其动力驱动系统要求具备极高效率以满足对驾驶条件变化的快速响应性，实验证明该控制系统对调速要求响应快速、准确，可实现永磁同步电动机基本调速功能。该系统可以经过后续的参数整定和算法优化，移植到整车环境下，以满足电动车的工作需求。

［1］Chan C C，Fellow.The State of Art of Electric and Hybrid Vehicle［J］.IEEE，2002，90（2）：247-275.

［2］Krishnan.Electric Motor Drives：Modeling，Analysis，and Control［M］.Upper Saddle River，NJ，Unite States：Prentice-Hall，2001.

［3］Bianchi N，Bolognani S，Zigliotto M.High-performance PM Synchronous Motor Drive for an Electrical Scooter［J］.IEEE Trans.on I.A，2001，37：1348-1355.

［4］Fu Minli.Design of Permanent Magnet Synchronous Motor for Electric Vehicle Drive［C］//Converter Technology&Electric Traction，2007：48-52.

［5］Gu Yu.Study and Design on Permanent Magnet Synchronous Motor Control System in Electric Vehicle［D］.Master.dissertation，Wuhan University of Technology，2007.

［6］Shiri A，Vahedi A，Shoulaie A.The Effect of Parameter Variationson the Performance of Indirect Vector Controlled Induction Motor Drive［C］//International Power Electronics and Motion Control Conference，IPEMC，2006：2377-2381.

［7］Bazzi A M，Friedl A P，Choi S，et al.Comparison of Induction Motor Drives for Electric Vehicle Applications：Dynamic Performanceand Parameter Sensitivity Analyses［C］//Electric Machines and Drives Conference，2009：639-646.

［8］Baburaj Karanayil，Uhammed Fazlur Rahman，Colin Grantham.Online Stator and Rotor Resistance Estimation Scheme Using Artificial Neural Networks for Vector Controlled Speed Sensorless Induction Motor Drive［J］.IEEE Transactions on Industrial Electronics，2007，54（1）：167-176.

［9］Haddounl A，Benbouzid M E H，Diallo D，et al.Comparative Analysis of Control Techniquesfor Efficiency Improvement in Electric Vehicles［C］//IEEE Vehicle Power and Propulsion Conference，2007：629-634.

［10］Peroutka Z，Zeman K，Krus F，et al.Control of Permanent Magnet Synchronous Machinewheel Drive for Low-floor Tram［C］//in 13th European Conference on Power Electronics and Applications（EPE），2009：1-9.

［11］Belin S，Scrooby M，Masselus J，et al.A PMSM Based Control for Tractionapplications［C］//in European Conference on Power Electronics and Applications（EPE），2003：952.

［12］Marufuzzaman Reaz，Ali.FPGA Implementation of An Intelligent CurrentdqPI Controller for FOC PMSM Drive［C］//Conference on Computer Applications and Industrial Electronics，2010：602-605.

［13］Chen Yiguang，Wang Luyi，Kong Lingbing.Research of Position Sensorless Control of PMSM Based on High Frequency Signal Injection［C］//Electrical Machines and Systems，2008：3973-3977.

［14］XU Yinglei，Li Quanzhan，Zhang Liyan，et al.Development of Permanent Magnet Synchronous Motor for Electric Vehicle［C］//Sustainable Power Generation and Supply，2009：1-5.

［15］Sharifian M B B，Herizchi T，Firouzjah K G.Field Oriented Control of Permanent Magnet Synchronous Motor Using Predictive Space Vector Modulation［C］//IEEE Symposium on Industrial Electronics and Applications，ISIEA，2009：574-579.