电力变压器油箱磁屏蔽的优化设计
2013-09-22程志光张俊杰
石 建 李 琳 程志光 张 栋 张俊杰
(1.华北电力大学,河北 保定 071000;2.保定天威集团,河北 保定 071056)
油箱磁屏蔽,即在油箱上放置由冷轧取向磁性电工钢带叠积起来的条形叠片组。叠片组通常有两种叠片形式,一种是平行油箱叠片,一种是垂直油箱叠片。无论哪种叠片组都为漏磁场(特别是绕组漏磁场)构成了一个具有高磁导率、低损耗的“磁分路”,引导漏磁通通过该“分路”,降低了进入油箱箱壁的漏磁通。如果合理的放置磁屏蔽,就会有效地减少油箱中的磁滞损耗和涡流损耗。
随着原材料成本的不断提高,以及市场竞争的日益激烈,电力变压器厂家正在努力推行精细化设计来提高产品效能。油箱磁屏蔽由材料及制作工艺决定了其占有变压器成本中一定的比重。所以,在油箱磁屏蔽设计时,找到其效能与成本的结合点尤为关键。
国际计算电磁学会TEAM基准问题族(Problem 21 Family)中的Problem 21c(以下简称P21c)的直接工程背景就是大型电力变压器中广为采用的磁屏蔽和电磁屏蔽,该基准问题的建立使考察“单片级”薄层内的损耗、涡流、磁通的波形和分布的实际情况、变化规律成为可能。所获得的面向解决大型电磁场问题的策略和计算结果、结论,有助于合理建立有限元分析模型,验证各种情况下的电磁场和损耗计算方法的有效性。

图1 二维变压器计算模型
电力变压器设计人员在针对一台世纪的电力变压器做工程设计时,首先根据要求设计出变压器的所有参数,然后通过各种方法对设计方案进行验证。油箱磁屏蔽这部分设计通常放在线圈、铁心、绝缘、油箱等部件设计之后进行。
考虑到零件的通用性和生产的工艺性要求,磁屏蔽条的宽度通常采取定值。所以在电力变压器油箱磁屏蔽工程设计和方案校核计算过程中,只需根据需要确定磁屏蔽的厚度。具体设计步骤是,首先建立电力变压器计算模型(如图1所示),然后使用有限元分析软件进行计算变压器的漏磁场分布。调整磁屏蔽厚度使其中的磁通密度在1.7T左右,从而保证损耗在合理的范围之内,且不出现局部过热,同时保证磁屏蔽的方案为最优。在有限元计算过程中,设计人员需要多次改变模型中磁屏蔽厚度,来满足其磁密要求,具体设计流程如图2所示。

图2 磁屏蔽设计流程
在此过程中,更改模型、有限元计算虽然是简单的重复性工作,但花费了设计人员的大部分精力和时间,如果此过程交给软件自动完成,将会节省很大的人力成本和时间。通过使用计算机优化仿真软件,得出理论上的最优方案,以供设计者分析、使用。
1 关于优化仿真软件
目前一般主流的有限元仿真软件只具备单一的有限元仿真运算功能,不具备优化功能。所以需要引入第三方的优化软件来解决问题。
优化软件帮助设计人员实现改进或全新产品设计,需要具备以下基本功能:
1)参数化模型。
2)多变量的设定。
3)与仿真软件的无缝对接,耦合求解。
4)自动迭代。
OptiNet软件就是一款能够满足上述要求且易于使用的优化工具。将它与电磁仿真软件 MagNet,ElecNet, and ThermNet紧密整合在一起,可以实现互相之间的无缝对接。
2 应用实例
以某双圈无载发电机变压器SFP-140000/220为例,使用OptiNet结合MagNet,对其进行磁屏蔽的优化设计。在其主要参数确定以后,进入磁屏蔽设计阶段。步骤如下。
1)首先建立二维模型,导入MagNet磁场计算软件。定义其材料、设定边界条件后,加入激励源。如图3所示。

图3 变压器模型
2)对于磁屏蔽的厚度,不妨设为参数 t。首先在模型的整体属性中引入参数t,类型为number数字型,随意设定其值,如10mm,如图4所示。
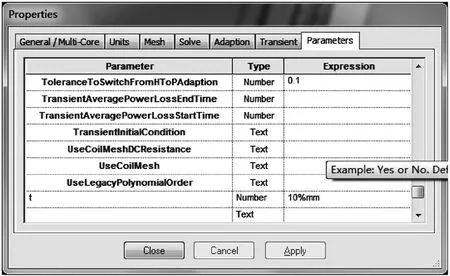
图4 整体模型的属性
3)因为磁屏蔽是固定在油箱箱壁上(如图5所示),所以磁屏蔽油箱侧上下两点A、B坐标为定值,A(985,1184),B(985,-1133)。内侧两点 A'、B'到A、B的距离即为磁屏蔽的厚度t,所以定义A'、B'的横坐标就定义了磁屏蔽的厚度。在A'、B'两点的属性中定义它们的坐标,并标明与 A、B两点的距离为 t,并保存。A'、B'两点的坐标分别为(985-t,1184),(985-t,-1133)。
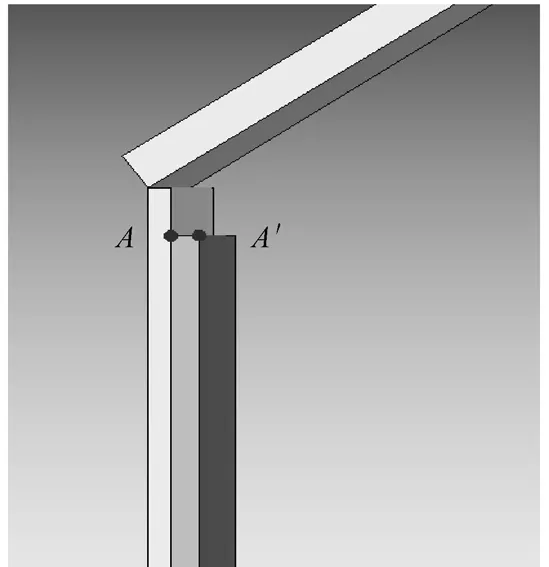
图5 磁屏蔽上端两点A和A'
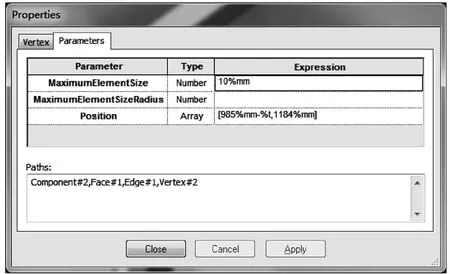
图6 定义A'的坐标
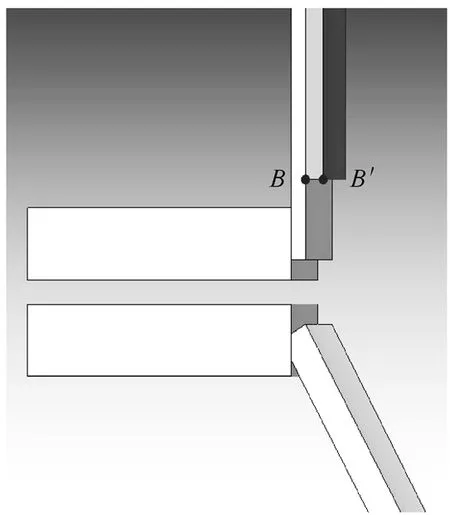
图7 磁屏蔽下端两点B和B'
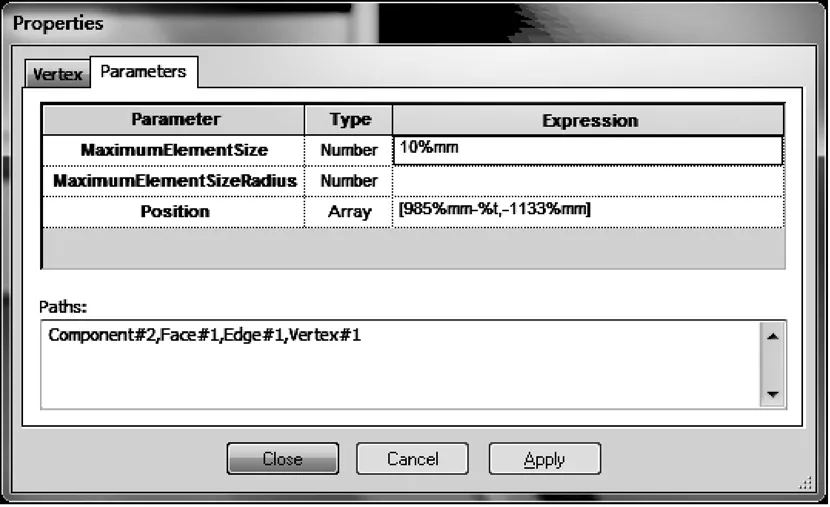
图8 定义B'的坐标
4)运行 OptiNet,打开 MagNet保存的模型,选择2D时谐场运算。

图9 OptiNet主界面
5)在变量页面,定义变量t,类型为continuous连续型。根据经验设定初始值8mm,规定其范围为1~30mm。
6)关于磁屏蔽中的磁密,可以在磁屏蔽中设置采样点来确定。例如将磁屏蔽高度方向对应线圈的中心、厚度方向中间层的中点设为采样点,坐标为(958-t/2,0)。在目标页面,选取目标为“某点场值误差的绝对值”。由于使用时谐场计算,所以在相角为0°时磁场强度最大。在argument列中设置判据:在点(958-t/2,0)当0°时磁场强度B与1.7T的偏差绝对值;目标goal选择最小minimize。输入时应注意其格式。
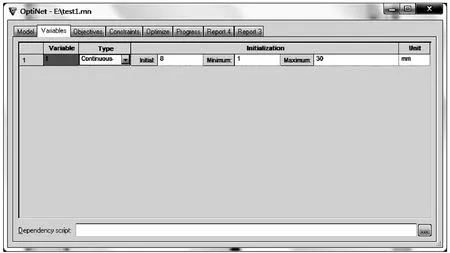
图10 变量设定页面

图11 目标设定页面
7)在Optimize优化页面,点击Start Optimization按钮就可以开始进行优化计算。另外,在此页面中,还可以规定最大方案数量、偏差、时间限制等参数,来根据需要改变其优化的精度和运行时间。

图12 优化设定界面
8)优化过程开始后,progress过程界面可以看到其自动迭代运算的过程。每一组solution,即每一次迭代运算,都分别有对应的目标(goal)、变量(variable)、目标值(objective)。优化的的过程,在图中以“*”点记录下来,输出最终优化结果。
9)当计算出最优化结果后,程序自动停止。报告页面输出记录了优化过程的参数,如图15所示。可以看到,经过反复迭代81次计算后得出最优方案,计算过程仅历时236s,最优磁屏蔽厚度约为6.416mm。工程设计中可以参考此数值设计磁屏蔽的厚度。

图13 迭代中的goal参数和优化输出的goal参数

图14 迭代中的变量t和优化输出的变量t

图15 迭代中的objective参数和优化输出的objective参数

图16 报告中的数据
3 结果验证
返回 MagNet程序,打开整体模型的属性,可以看到当初设定的变量t已经改为优化后的数值。
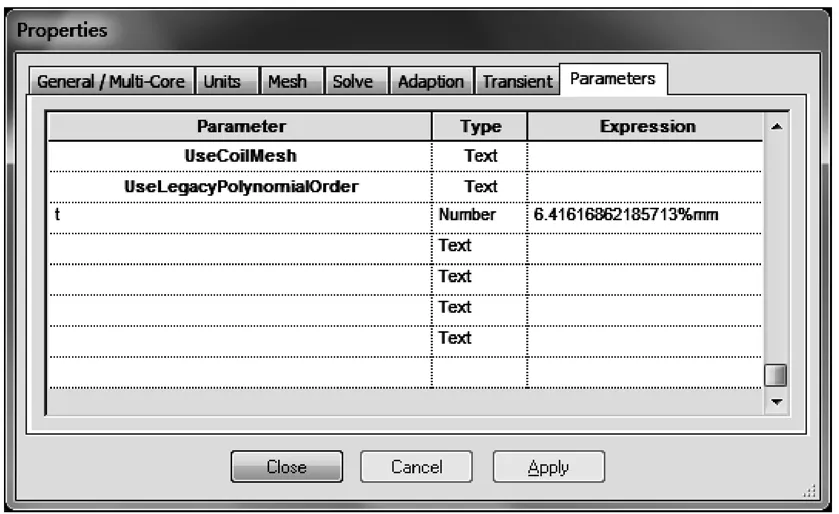
图17 整体模型的属性
磁场仿真计算已经算出了结果,磁屏蔽中的磁密在1.7T左右。

图18 磁场云图

图19 磁屏蔽中的磁密
4 结论
结合产品设计需要,采用成熟的电磁场分析和优化软件,实现变压器油箱磁屏蔽的优化设计,取得了有指导意义的结果,提高了设计计算效率,同时又得到了较高精度的结果,具有很高的实用价值。
大型变压器磁屏蔽的三维建模、数值分析和优化设计是作者进一步的研究课题。
[1] 谢毓诚.电力变压器手册[M].北京:机械工业出版社,2003.
[2] 程志光,高桥则雄,博扎德· 弗甘尼.电气工程电磁热场模拟与应用[M].北京:科学出版社, 2009.
[3] TUROWSKI J, LOPEZ-FERNANDEZ X M, SOTO A,SOUTO D. Stray losses control in core-and shell type transformers [J]. Part I: Upgrading of energy-saving and reliability of large transformers, ARWtr2007,29-31 October 2007. Baiona-Spain.
[4] CHENG Z, TAKAHASHI N,FORGHANI B, LIU L,FAN Y, LIU T, ZHANG J, WANG X. 3-D finite element modeling and validation of power frequency multi-Shield Effect[J]. IEEE Transaction on Magnetics,2011, 47(5): 1346-1349.
[5] Infolytica Corporation, OptiNet 7. 1. 2 help manual.
[6] Infolytica Corporation, Optimization of Die Press Model TEAM Problem 25 Tutorial, March 23, 2010.
[7] Infolytica Corporation, Minimizing cogging torque in a brushless motor, March 23, 2010.
[8] Infolytica corporation, Optimize the design of a loudspeaker, March 23, 2010.
[9] 保定天威保变电气股份有限公司组编,赵静月主编,变压器制造工艺,北京:中国电力出版社,2009.
[10] K. KARSI D. SC., D.KERENYI D. SC., L.KISS D. SC.合著,王晓莺译,胡启凡,王显文校,大型电力变压器.
[11] TAKAHASHI N, SAKURA T, CHENG Z. Non-linear analysis of eddy current and hysteresis losses of 3-d stray field loss model (Problem 21) [J].IEEE Trans. on Magn., 2001, 37(5):3672-3675.
[12] CHENG Z, TAKAHASHI N, YANG S, et al. Loss spectrum and electromagnetic behavior of Problem 21 family [J]. IEEE Trans. on Magn., 2006,42(4):1467-1470.
[13] 耿荣林.电力变压器漏磁场及箱体涡流损耗的有限元分析[D].沈阳工业大学硕士学位论文, 2008, 2.
[14] CHENG Z, HU Q, GAO S, et al. Stray-field loss analysis and measurement (Problem 21) [A]. Proc of the International TEAM Workshop [C]. Berlin, 1995:62-66.
