基于磁耦合谐振无线能量传输系统传输效率的研究
2013-09-22黄诗宗汤宁平王建宽
黄诗宗 汤宁平 王建宽
(福州大学电气工程与自动化学院,福州 350108)
无线能量传输(Wireless Power Transmission,WPT)是借助于电磁场或电磁波进行能量传递的一种技术。该电能传输技术免除了供电电源与用电负载之间的直接金属导体连接,实现电能的无线通达。无线供电可以避免身体直接接触插座或者裸露的导线所导致的用电事故。通过对设备无线供电,可以有效的避免电弧或者电火花在易燃、易爆场合下引起的用电安全事故。此外,无线电能传输技术可还以为各类移动电气设备、工作于水下等特殊环境下的电气设备提供可靠的电能供应。因此,发展无线电能传输技术的重要性日益凸显出来。
目前,根据无线能量传输原理,可将无线能量传输方式分为3类:电磁波无线能量传输技术、感应式无线能量传输技术、磁耦合谐振式无线能量传输技术。磁耦合谐振式无线能量传输技术是最近几年才被提出的世界前沿课题,它与其他能量无线传输技术相比的优势:①与电磁感应原理的电能无线传输技术相比,传输距离大大提高;②与利用微波原理的电能无线传输技术相比,将微波无线电能传输毫瓦数量级功率提高到几十瓦至几百瓦的数量级。因此磁耦合谐振无线能量传输在中距离的电能传输上具有突出的优势[1]。
然而现阶段磁耦合谐振无线能量传输技术处于起步阶段,目前国内外对该技术有些初步研究[2-4],但对影响传输效率的诸多因数的分析不够全面。本文通过空间线圈等效耦合模型分析负载RL,谐振线圈的空间距离 d,电源频率 f对系统传输效率的影响,并用实验验证了理论分析的正确性,并在该分析的基础上设计制作高效率磁耦合谐振系统。
1 磁耦合谐振无线能量传输的原理介绍
磁场耦合谐振无线传输技术是感应式无线传输技术上融合了谐振技术。传递能量的两个线圈是空心线圈,线圈的耦合属于松耦合,耦合系数很小。在某一频率下,通过对两个能量传输的线圈进行并联或者串联电容进行补偿,使得空间上两个分离的线圈都同时产生谐振,两个相同谐振频率的谐振物体间能产生更强的耦合,从而使得能量在两个谐振线圈之间更高效的传递。
在谐振耦合无线输电系统中如图1所示,用一定频率的高频电源给系统供电,在这一频率下,发射和接收端的选择合适的补偿电容,使得谐振耦合能量无线传输的2个线圈发生谐振;即发射端与接收端的等效电路发生谐振,线圈回路阻抗达到最小值,从而使大部分能量往谐振路径传递到负载。

图1 磁耦合谐振无线电能传输系统
2 磁耦合谐振无线能量传输系统建模与传输效率推导
利用互感耦合模型来进行磁耦合谐振无线能量传输系统的建模,谐振线圈等效为一个电感与一个电阻的串联,将发射线圈定义为原边线圈,将接收线圈定义为副边线圈,用互感来表示原副边磁耦合的强度[5]。如图2所示。本文对原、副边线圈都采用串联谐振补偿(以下简称 PSSS),并对这种补偿拓扑的传输效率进行理论建模分析与实验验证,图2为PSSS补偿磁耦合系统原理图。
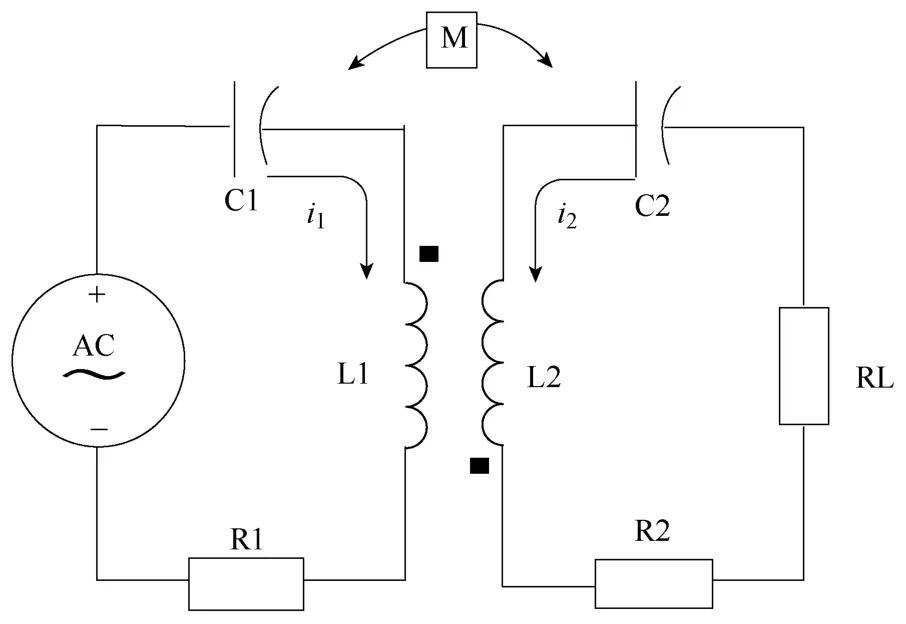
图2 PSSS补偿的磁耦合系统
磁耦合谐振能量传输系统的频率属于高频,空心谐振线圈的等效内阻不可忽略,原边谐振线圈等效为电感 L1与电阻 R1,副边线圈等效为电感 L2与电阻 R2,原副边的补偿电容分别为 C1与 C2。补偿电容实际应用可以选取高频电容,具有很低的损耗电阻,忽略补偿电容的电阻。两空心线圈的互感与线圈的匝数、尺寸、空间位置有关。在传输距离一定的情况,两线圈固定,两线圈的互感系数即可认为是一固定值,取为M。副边负载为纯电阻RL,电源电压Uin。
在如图2所示的PSSS磁耦合电路模型中,根据网孔法可列方程[6]

原边等效阻抗:

副边等效阻抗:
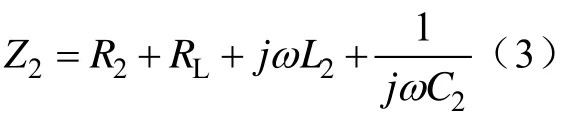
根据式(1)的方程可得到
原边回路电流:

副边回路电流:

电源的输入功率:

负载输出功率:

PSSS磁耦合系统的传输效率:
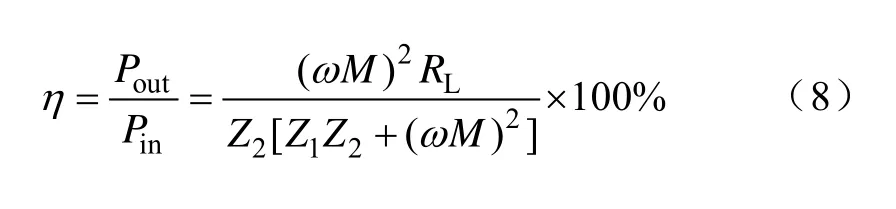
根据以上 PSSS磁耦合系统的传输效率的表达式(8)可以看出,传输效率受原副边阻抗的影响,只有当原副边线圈同时谐振,整个耦合系统处于完全谐振的状态,此时原副边回路的阻抗最小,此时传输效率最大。
3 影响磁耦合系统传输效率的关键因素分析与验证
从PSSS系统传输效率的理论分析式(8)表达式来看,在谐振耦合系统的线圈的匝数尺寸、补偿电容选定,即确定耦合传输系统原副边电感L1、L2,内阻R1、R2,补偿电容C1、C2的情况下,互感M,负载 RL,ω是影响谐振系统传输效率的关键变量。输入电源频率 f决定 w;两谐振线圈在空间位置上采用同轴平行排列,两线圈的互感为[7]

式中,r1, r2为线圈的半径,N1, N2为线圈的匝数,
因此,影响磁耦合系统传输效率的关键变量是电源频率f,负载阻抗RL,空间线圈距离d。
本设计试验装置磁耦合系统的发射与接收的谐振线圈采用圆柱形密绕空心线圈,其参数为:导线半径a=1.0mm,线圈半径R=14.5cm,线圈匝数n=9,绕制相同原副边谐振线圈(忽略制作上的差异),分析测的线圈的电感L=61μH,线圈内阻R0=0.2Ω,原副边补偿电容选取无感高频电容,容值0.047μF。
确定系统电感、补偿电容的参数L1=L2=61μH、C1=C2=0.047μF,根据传输效率的推导式(8),利用MathCAD 14工程计算软件进行分析计算,得到PSSS系统传输效率关于电源频率f、负载阻抗RL、空间距离d的关系曲线分别为图4、图5、图6的三角形点状虚线。
基于上述的理论分析及绕制谐振线圈参数,采用SP1651的功率信号发生器做为交流电源,对理论计算的 PSSS系统相对于电源频率、副边负载、空间距离的传输效率进行实验验证。SP1651可以实现最高频率200kHz,最大100W功率的正弦波输出,满足实验要求。实验装置如图3所示。

图3 PSSS磁耦合谐振系统实验装置图
当固定线圈参数L1、L2互感M、补偿电容及系统负载RL;改变电源频率f,通过MathCAD 14计算不同电源频率的传输效率,并通过实验验证。实验和计算的得到不同电源频率的系统传输效率如图4所示,从该图可以看出PSSS系统传输效率在线圈与电容谐振频率94kHz附近最大,当电源频率偏离谐振频率时候,传输效率迅速下降。
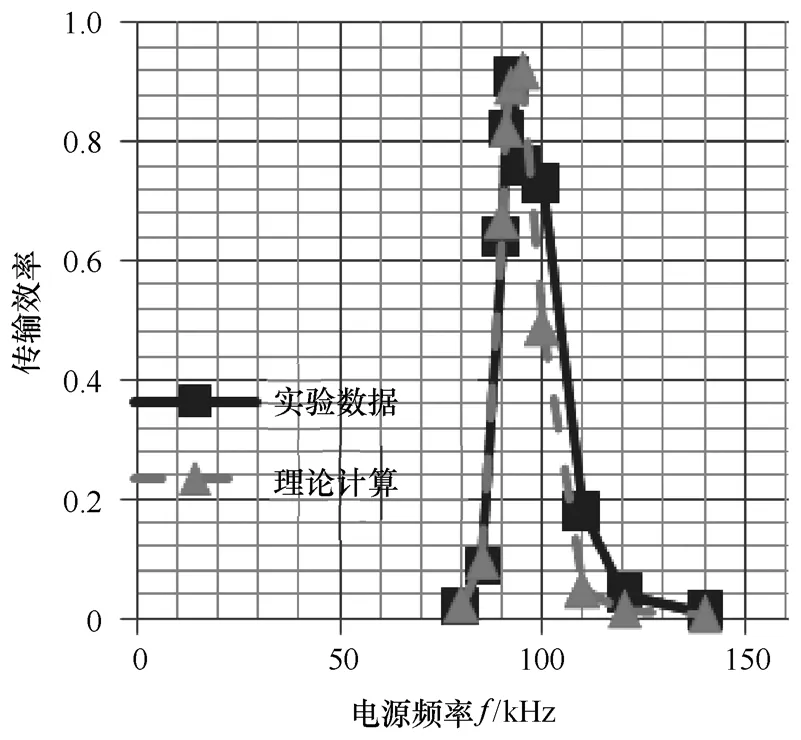
图4 PSSS系统传输效率与电源频率f的关系
当固定线圈参数L1、L2互感M、补偿电容,电源频率为线圈与补偿电容的谐振频率 94kHz。在不同负载情况下,传输效率的实验值和理论计算值如图5所示,从该图可以看出传输效率随负载电阻的增加先增大,达到一个效率的最高点,再减小,如图5所示。实验效率曲线与理论计算有较好的一致性,由于理论计算忽略了线圈的辐射损耗,实际空间两线圈的制作存在差异等因数造成实验的传输效率低于理论计算值。

图5 PSSS系统传输效率与负载RL的关系
当固定线圈参数L1、L2互感M、补偿电容,电源频率为线圈与补偿电容的谐振频率 94kHz,固定负载5Ω;实验和计算的得到不同电源频率的系统传输效率如图 6所示,可以看出PSSS系统的传输效率随着空间两线圈的距离的增大而减小,当距离越大下降的速度越快。

图6 PPSP系统传输效率与负载RL的关系
4 PSSS无线能量传输装置的设计制作
为了验证理论分析的正确性,本文设计制作了基于高压谐振控制器L6599的半桥逆变的串联谐振无线能量传输装置。如图7所示,该装置包括半桥逆变电源、距离为 10cm的空间线圈、线圈匝数 9匝、半径14.5cm,5Ω的阻性负载。

图7 基于L6599的半桥谐振逆变的串联谐振无线能量传输装置
调节L6599的外围振荡电路参数,当电路的振荡频率被设置在93.79kHz的时候,接收端负载的电压最大;该系统半桥逆变电路上下开关管的驱动波形如图 8所示,上、下管驱动电压分别为 11.2V、11.8V,频率为93.79kHz,两驱动波形有一定的死区时间,满足半桥开关管的驱动要求。接收端5Ω负载的电压波形如图9所示,其电压波形为频率92.99kH的正弦波,幅值为24.4V,有效值为8.66V。通过直流表测量24V开关电源的输出电流为0.718A,可计算的输入整机的输入功率为17.2W,5Ω负载的输出功率经计算为15W,该系统的传输效率达到87.1%。

图8 谐振逆变电路L6599的驱动输出波形
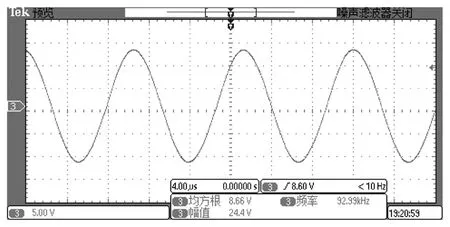
图9 接收端5Ω阻性负载的电压波形
5 结论
本文通过空间线圈等效耦合模型,推导了磁耦合谐振PSSS系统的传输效率,通过MathCAD软件分析系统能量传输效率与负载RL,空间线圈距离为d,电源频率为f的关系,并用实验验证了理论分析的正确性。通过该分析,设计制作了基于L6599的半桥逆变的串联谐振无线能量传输装置,该装置以直流 24V为供电电压,负载为 5Ω,实测传输功率为15W,传输效率达到87.1%。
[1] 杨庆新,陈海燕,徐桂芝,等.无接触电能传输技术及其应用[C]. 2009年全国电工理论与新技术年会(CTATEE'09).杭州, 2009-05-31, 2009: 379-385.
[2] 曲立楠.磁耦合谐振式无线能量传输机理的研究[D].哈尔滨:哈尔滨工业大学, 2010: 1-56.
[3] 林宁.无接触电能传输系统的设计研究[D].杭州:浙江大学, 2011: 1-105.
[4] CANNON B L, HOBURG J F, STANCIL D D, et al.Magnetic resonant coupling as a potential means for wireless power transfer to multiple small receivers[J].Power Electronics, IEEE Transactions on, 2009, 24(7):1819-1825.
[5] 傅文珍,张波,丘东元,等.自谐振线圈耦合式电能无线传输的最大效率分析与设计[J].中国电机工程学报,2009(18): 21-26.
[6] (美)亚历山大,(美)萨迪库.电路基础[M].北京:人民邮电出版社, 2009.
[7] 刘修泉,曾昭瑞,黄平.空心线圈电感的计算与实验分析[J].工程设计学报, 2008(2): 149-153.
