基波调谐式混合型有源电力滤波器主电路优化研究
2013-09-22刘桂英谢海丽
黄 飞 刘桂英 谢海丽 李 莎
(长沙理工大学电气与信息工程学院,长沙 410076)
随着电力电子技术的发展,各种各样的电子器件用于电力系统,电网的谐波危害已经到了一个相对严重的程度,然而科技的发展却对电能质量的要求日益严格,这样就行成了一个比较突出的矛盾,急需解决。对电力系统中的谐波进行滤波是一个效果好、相对简单的方法,现有的滤波器手段主要有:无源滤波器、有源滤波器以及混合型滤波器,然而传统的无源滤波器是基于谐振原理,结构相对简单,容易实现,经济性较好,但只能对特定次的谐波进行滤除,而且易与电网产生串、并联谐振,受电网影响严重。而有源滤波器则能动态的对谐波进行补偿,补偿效果好,稳定性好,但是直接与电网相连对其的电压、电流和容量都有比较高的要求,技术实现比较困难。混合型有源滤波器同时兼具无源和有源滤波器两者之优点,用无源滤波器滤除几次含量较大谐波,再用有源滤波器来补偿其他次含量较小的谐波,这样有源滤波器的容量可以做的较小,又可以得到较好的滤波效果。
本文基于对现有的各种有源滤波器的拓扑结构的分析,提出了一种基波调谐注入式混合有源电力滤波器,并运用动态规划—遗传算法对其主电路的各个部分进行了综合设计,最后进行了整体的仿真。
1 拓扑结构和原理
图1所示为基波谐振注入式混合有源滤波器的拓扑结构,有源部分是一个电压型逆变器,直流侧接一个大电容,采用 IGBT模块,通过一个输出电抗器接到耦合变压器。输出电抗器主要是抑制系统的电流突变和逆变器的产生的高频毛刺。有源部分通过耦合变压器与谐振支路并联,谐振支路在基波附近谐振,因此逆变器几乎不承受基波电压,其对于高频分量的阻抗则较大,这样有源滤波器产生的谐波分量能够很顺利的进入主电路。谐振支路通过注入电容和电网并联,注入电容承受了大部分的基波电压,还能像电网注入一定容量的无功。几组无源滤波器也并联接入电网,在电网含量较大的几次谐波附近谐振,滤除系统大部分的谐波,这样就大大减少了有源部分的容量,同时还能对系统进行无功补偿。该结构的混合型有源滤波器,是由无源滤波器和有源滤波器来滤除谐波,由注入电容和无源滤波器来补偿无功。
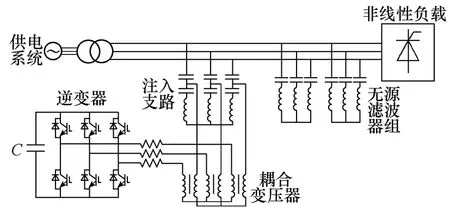
图1 基波谐振注入式混合有源滤波器的拓扑结构
2 遗传动态规划的多目标优化
动态规划算法和遗传算法是两种比较成熟的优化设计算法,应用都比较广泛,但是各自有其优势和缺点。动态规划算法是一种解决多阶段决策最优的方法,对于多目标的优化问题,可以将多个目标分为多个阶段,每个阶段都求出其最优解,综合在一起即整个多目标问题的最优解,但是动态规划算法是单独对某个阶段进行求解,没有从全局来考虑,因此得到的解只是局部最优解,很难的到全局最优解。遗传算法是一种模拟生物进化的优化算法,其本质是一种高效、并行、全局搜索的方法,它能在搜索过程中积累和自动获取搜索空间的有关知识,并控制搜索过程以求得最优解,具有很强的全局寻优的能力。但初值的选取是在一个特定的数值空间内随即产生,适应度不高,需要很多次的迭代运算才能得到最优解,这将会产生很长的迭代亢余,不利于快速准确的寻得全局最优解。本文将动态规划算法和遗传算法结合起来,通过动态规划的多阶段决策得出一系列适应度较高的初始值,再用遗传算法对这些初始值进行迭代运算,最终能够快速、准确的得出多目标问题的全局最优解。
2.1 目标模型
基波谐振注入式混合有源滤波器的优化设计是一个多目标非线性的求解问题,需要同时考虑滤波器的经济性函数、满意度函数和无功补偿函数这三个目标,在一定的约束条件下同时达到最优。
1)经济性函数。以基波调谐式混合型有源电力滤波器的整体造价为优化的目标函数,设计的变量主要是滤波器的各个支路的电容和电感容量。目标函数的表达式如下:

式中,KC、KL分别为电容器和电感的单位造价,C1、CC、CL、CN分别为:注入电容、谐振支路电容、无源支路电容和逆变器直流侧电容,QL1、QLL为注入支路电感和无源支路电感。
2)满意度函数。对一个滤波器的满意程度,主要是依靠其滤波器的滤波的滤波器性能来决定的。如果滤波器能够很好的滤除系统中的谐波,使其谐波含量低于国家标准,则其满意度就高。通过混合型有源滤波器的作用,使得系统总的谐波含量满足国家规定的标准,尽量使其达到最小。本文将谐波电压、电流的总畸变量作为标准:

THDU、THDi为电压、电流的总畸变,THDu,max、THDi,max分别为国家标准的电压、电流总畸变的上限值。
3)无功补偿也是混合型有源滤波器的一个重要的指标,无功补偿的容量因该按照系统中的无功缺额来分配,不能过补偿也不能欠补偿,因尽量使得补偿后的功率因数能够接近1。通过下式来整定:
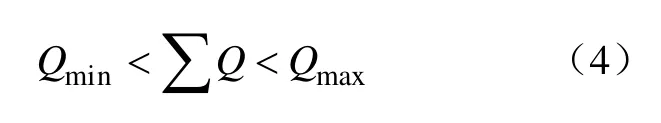
式中,∑Q为滤波器向系统所注入的无功总量(包括:各次PPF所注入的无功和注入电容提供的无功),Qmin、Qmax分别为补偿无功的上限和下限。
约束条件:
1)逆变器直流侧的电容
逆变器直流侧的电容为逆变器提供稳定的直流电压,让逆变器能够实时的发出有效的谐波电流。理论上,直流侧电容越大,其提供的电压也就越稳定,但电容越大,其体积也将越大,成本也会提高很多,实用性也不强。因此,直流侧电容必须要能满足逆变器的补偿能力,必须要留有一定的裕度,但也不能过大,如下式所示:
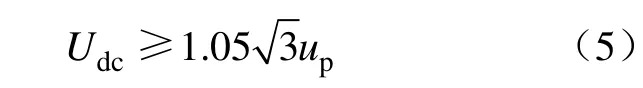
式中,up为逆变器期望输出电压峰值。
2)逆变器IGBT开关频率
IGBT是逆变器的主要组成部分,它的开关频率直接影响到了它的输出性能。开关频率太高,逆变器的损耗太大;开关频率低,逆变器的输出不能满足要求,因此,逆变器开关频率要满足:
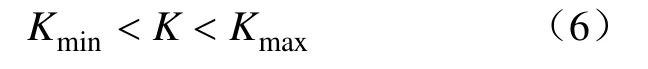
综上所述,得到目标的适应度函数如下:
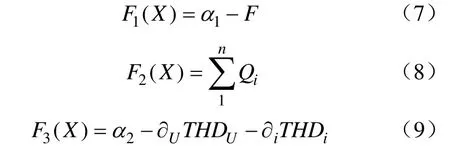
约束条件:
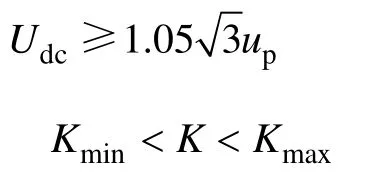
式中,α1、α1是较大的正数,用来保证F1(X)、F1(X)始终为正值,其值可根据经验确定;∂U和∂i均为大于零的常数,用来匹配电压、电流总畸变率的权重,一般 ∂U:∂i1:100。
2.2 动态规划确定多目标优化问题的初始解
对多目标的优化问题应用动态规划求解,将多目标优化问题分为三个阶段,第一个阶段为滤波器的整体滤波效果,即满意度函数F3(x),求出一组最优解;第二阶段为滤波器的无功补偿效果F2(x),在第一阶段求出最优解的制约下,求出无功补偿的最优解;第三阶段为滤波器的整体经济性F1(x),在第二阶段求出最优解的制约下求出经济性的最优解,然后多次循环求解,得出滤波器的多目标的一组适应度较高的初始值。
算法的基本步骤:
1)初始化系统原始数据。
2)考虑约束条件,对满意度函数 F3(x)进行求解,得到最优策略P。
3)对无功补偿函数F2(x)进行求解,在F3(x)函数的解P的宽容范围内求出、关于F2(x)的最优策略S。
4)对经济性函数F1(x)进行求解,在F2(x)函数的解S的宽容范围内求出关于F1(x)的最优策略H。
5)进行多次迭代,直到输出结果满足适应度的要求。
2.3 遗传算法解出多目标问题的最优解
遗传算法计算前需要做下面准备:
1)适应度函数的建立。前面已经建立了滤波器多目标优化设计的适应度函数:F1(x)、F2(x)、F3(x)。
2)染色体编码。染色体是遗传算法优化设计的信息载体,本文采用实数编码,考虑滤波器的主要的参数设计,其电容值确定了,其他的参数都将能够很好的确定,所以本文以各支路的电容器参数为变量,因此染色体可以用一组n维的向量表示,如下:
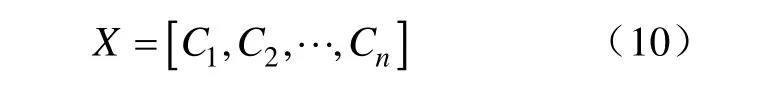
3)遗传参数的选择。为了避免遗传算法早熟陷入局部最优,本文采用变化的交叉、变异率进行操作,让他们随着染色体的适应度值变大而减小;适应度值变小而增大。公式如下:
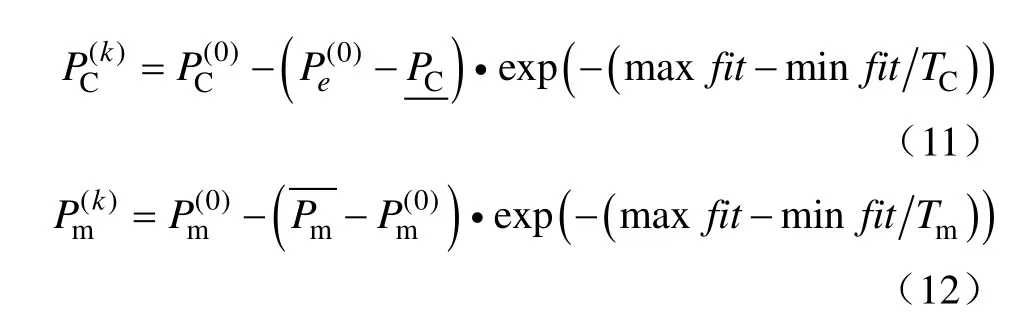
设 f1i、f2i、f3i是函数 F1(x)、F2(x)、F3(x)关于 i染色体的值,在寻优过程中为了得到全局最优解,除使种群向 f1i较大的方向进化,还要保证 f2i和 f3i的取值能够确定较好的基因。对于第 t代染色体进行如下操作:
1)保留良种,对于满足 f1i、f2i或 f3i的染色体以100%的概率遗传到下一代;
2)保留满足α3min<f2i<α3max和α2min<f3i<α2max的染色体i,也就是保留了f2i和f3i适应度较好的染色体,期望能够遗传出f1i适应度较好的染色体;
3)对于满足α2min<f3i<α2max但是不满足α3min<f2i<α3max的染色体,以概率PJ1进行遗传选择;
4)对于满足α3min<f2i<α3max但是不满足α2min<f3i<α2max的染色体,以概率PJ2进行遗传选择;
5)对于即不满足α2min<f3i<α2max同时也不满足α3min<f2i<α3max的染色体,以概率PJ进行遗传选择;
6)在上述的操作完成后,为了保证种群的规模不变,根据染色体的数量,复制一部分染色体来补足种群。
上述过程中PJ2、PJ3和PJ的值如下所示。

动态规划和遗传算法相结合的优化流程图如图2所示。
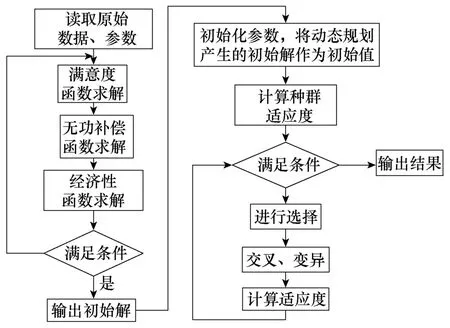
图2 动态规划-遗传算法流程图
3 实例
根据某电石厂的实际情况,应用上述方法进行谐波抑制和无功补偿。利用Matlab中的Simulink建立基波调谐式混合型有源电力滤波器的模型进行仿真,图 3、图 4分别为投入滤波器器前后系统的电压波形图,可以得出通过本文算法设计的滤波器具有很好的滤波性能。

图3 投入装置前系统的电压波形

图4 投入装置后系统的电压波形
4 结论
本文提出一种基波调谐式混合型有源电力滤波器,分析了它的拓扑结构和工作原理。着重运用了动态—遗传算法对其进行了优化设计,在保证其滤波和无功补偿效果的基础上,达到很好的经济性。经过仿真结果,论证了通过动态—遗传算法设计的混合型有源滤波器具有良好的滤波和无功补偿的能力,同时还能达到减少投资的效果。
[1] 王兆安,杨军,刘进军.谐波抑制与无功补偿[M].北京:机械工业出版社, 1998.
[2] 范瑞祥,罗安,李欣然.并联混合型有源电力滤波器的系统参数设计及应用研究[J].中国电机工程学报,2006, 26(2): 1-5.
[3] 帅智康,罗安,范瑞祥,等.注入式混合有源电力滤波器的注入支路设计[J].电力系统自动化, 2007, 31(5): 1-5.
[4] 刘博,周建中,杨敬涛.基于动态规划和遗传算法的混合算法研究[J].计算机仿真, 2004, 21(12): 87-89.
[5] 刘丽丽,田铭兴,叶建亚.新型混合有源电力滤波器参数设计[J].电气传动自动化, 2010, 32(3): 17-22.
[6] 范瑞祥.混合型有源滤波装置设计与应用研究[D].长沙:湖南大学, 2005.
