混流式水轮机组的模糊滑模控制

杨敏军

（三峡大学电气与新能源学院，湖北宜昌443002）

1 引言

随着低碳环保时代的到来，低能耗的发电厂将会有更大的发展前途，其中尤以核电厂与以生产再生能源形式的企业为主。目前，零碳发电厂的水电能源占世界电能的19%［1]，在很大程度上解决了能源短缺问题。一般情况下，一个典型的水力发电系统由水库、引水管道、调压室、水轮机、调速器、发电机以及电网组成。该系统是一个集水力、机械能与电能相交织在一起的复杂的动态系统［2]。由于工作的状态不同，系统内部参数也会随着外部环境变动而变化。也正是因为这种特性给设计性能更好的调速系统带来了很大的困难。正如很多水电行业的专家认为，水电站中关键设备之一就是调速器。最近十几年水轮机调速器控制方法已经有很多种探讨，总的来说可以分为两类［3]。一类就是比例、积分、微分型(PID)调速系统；另一类就是状态反馈或者称为智能型调速系统（IC）。经典PID调速系统着重于系统输出量，根据当前时刻的误差量（P）、误差累积量（I）以及误差的变化速率（D）来调整控制输入量。该方法丢失了该系统内部信息，现代控制理论不仅利用输出量信息，而且把系统内部状态作为参考从而更好地达到对输出量理想的控制效果。随着智能控制理论的发展，如预测控制、智能控制、鲁棒控制等[1-3]，这些控制技术逐渐应用于水轮机调速系统。

滑模控制（SMC）是一种变结构控制（SVC），是一种利用切换频率很快的开关控制策略来对动态的非线性系统完成非线性反馈控制方法［4]。滑模控制最大的优点在于它有很好的鲁棒性。对于水轮机调速器抗干扰性能方面有很大改善。但是，“抖振”问题一直是单一滑模控制的最大缺点。本文将模糊控制和滑模控制相结合，不但解决了该问题，而且使调速系统对干扰和参数变化具有很好的鲁棒性。

2 水轮机调节系统数学模型

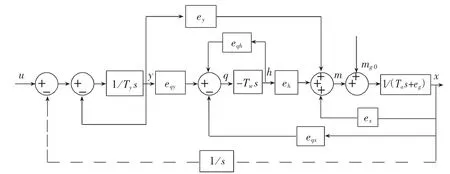
图1 水轮机调节系统框图

如图1所示为某一水轮机组系统单机带孤立负荷时的框图，该系统主要由电液随动系统、引水系统、水轮机系统、发电机、电网等组成。在小波动情况下可用线性模型来分析其结构。图1中u为控制输入信号，h为水头相对偏差值，x为转速相对偏差值，y为接力器行程相对偏差值，q为流量相对偏差值，mt为水轮机主动力矩相对偏差值，mg0为负载扰动，Ty为接力器时间常数，Ta为发电机转动惯量时间常数，Tw为水击时间常数,eg为发电机负载自调节系数，s为拉普拉斯算子，其他水轮机传递函数因子。

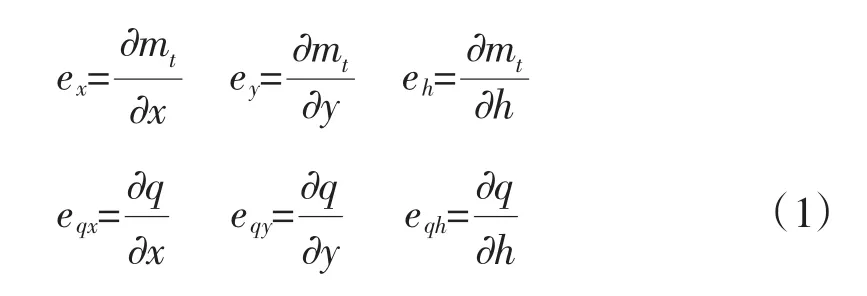
电液随动系统传递函数［5]为：

水轮机及引水系统函数［5]为：

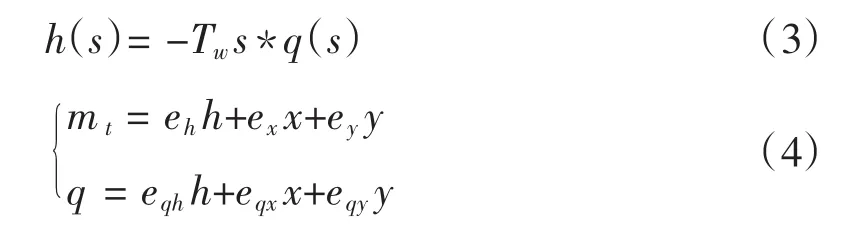
发电机与及电网传递函数［5]为：

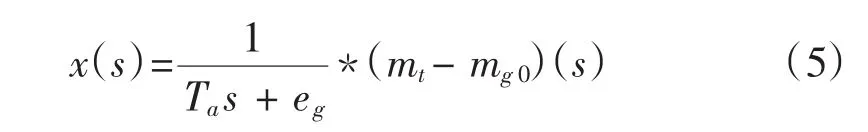
选 x、mt、y 分别为状态变量x1、x2、x3，另外增加一个附加变量x4［6],且x4定义如下：

则由以上可知系统状态方程为：

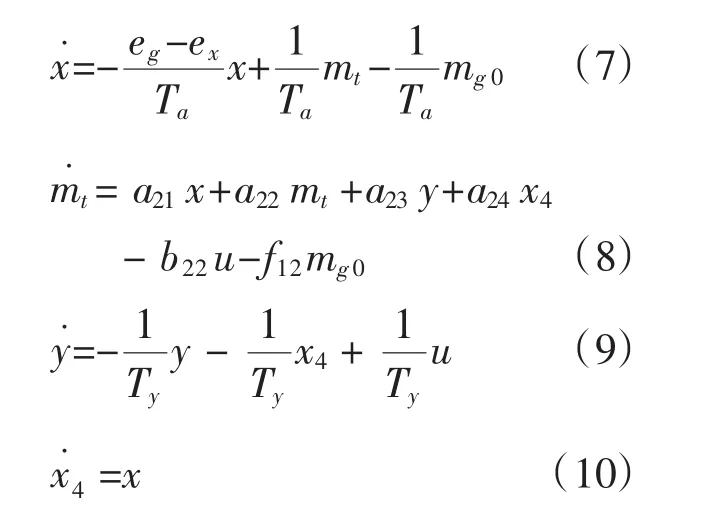
写成矩阵方程

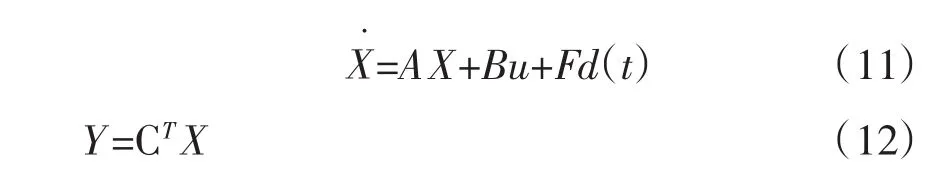
其中

3 滑模控制器设计

一般而言，滑模控制由两部分组成：开关控制和等效控制［7]。其中开关控制可使系统状态量向一个特定面滑动，等效控制则保证系统状态量始终在该滑模面上运动，并且最终渐进稳定。定义控制量u为:

其中：usw为开关控制，ueq为等效控制。

首先，定义一个滑模面s，如下式所示：

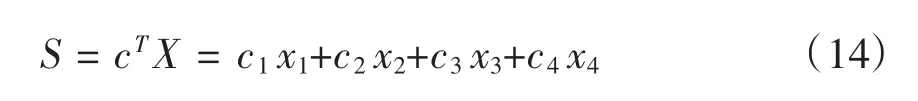
当系统状态滑向滑模面时，只有等效控制ueq作用,让S对时间t的导数为零，可得：

联合式（11）可得：

为了满足式（13），定义Lyapunov函数为：

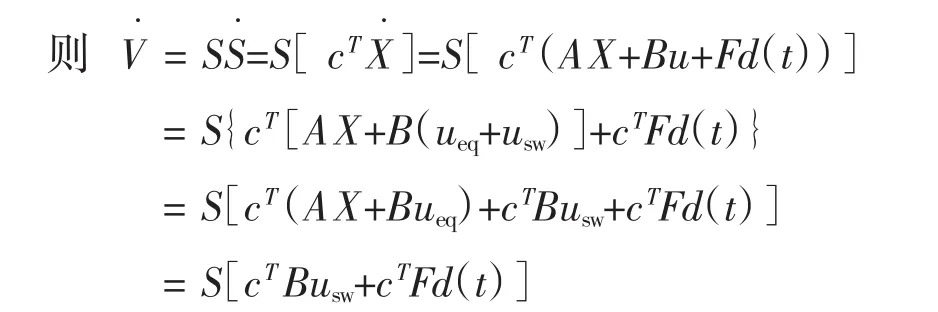
令cTBusw＝-kS-ηsgn（S）,这里k和η是正常数,sgn（·）是符号函数，则

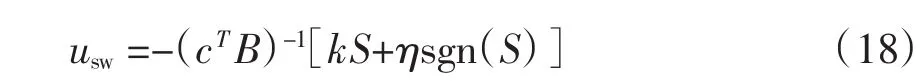
则控制量u为：

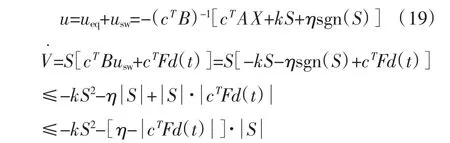
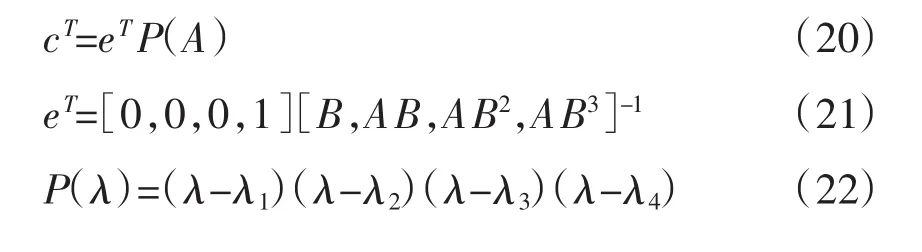
由Ackermann公式［4]可得：由于n=4，则 λ1＝-1，λ2＝-2，λ3＝-3，λ4＝-4，从而可计算出cT,滑模控制器设计完毕。

4 模糊控制接口系统设计

由文献［4]可知，模糊滑模控制能够消除或减弱常规滑模控制器中因 k固定时引起的“抖振”问题。由滑模存在条件为：设计如下模糊系统：选系统输入,△k为系统输出,模糊系统规则库定义如下：

其中：PB、PM、ZO、NM、NB分别表示负大、负中、零、正中、正大。

模糊输入、输出隶属函数分别如图2、3所示。

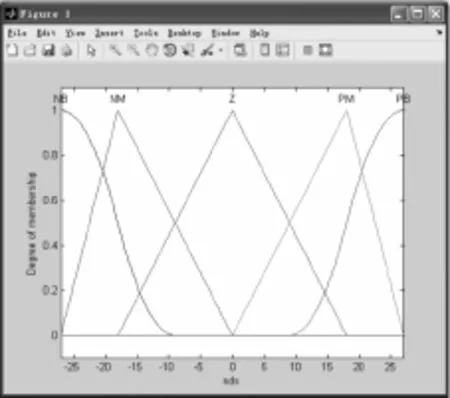
图2 模糊输入的隶属函数

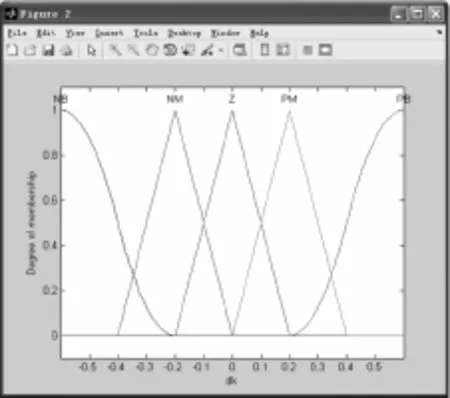
图3 模糊输出的隶属函数

由模糊控制系统整定后的k定义为：

由于k为正常数，△k的论域为[-0.6 0.6]，故k0≥1.2。

5 系统仿真结果

针对某一水电站的水轮机调速系统参数在单机带负荷的情况下，应用Matlab仿真。其参数如下表1所示。

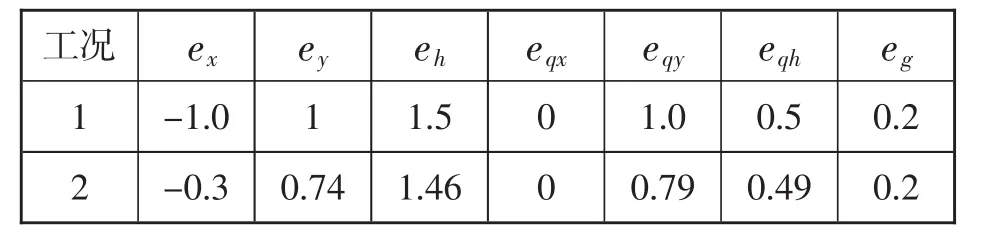
表1 参数表

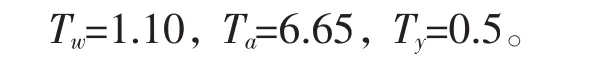
为了节省仿真算法时间,取η＝0.2,在负载扰动为10%的情况，工况一时各状态变量与控制输入u的曲线如图4所示，工况二时各状态变量与控制输入u的曲线如图5所示。

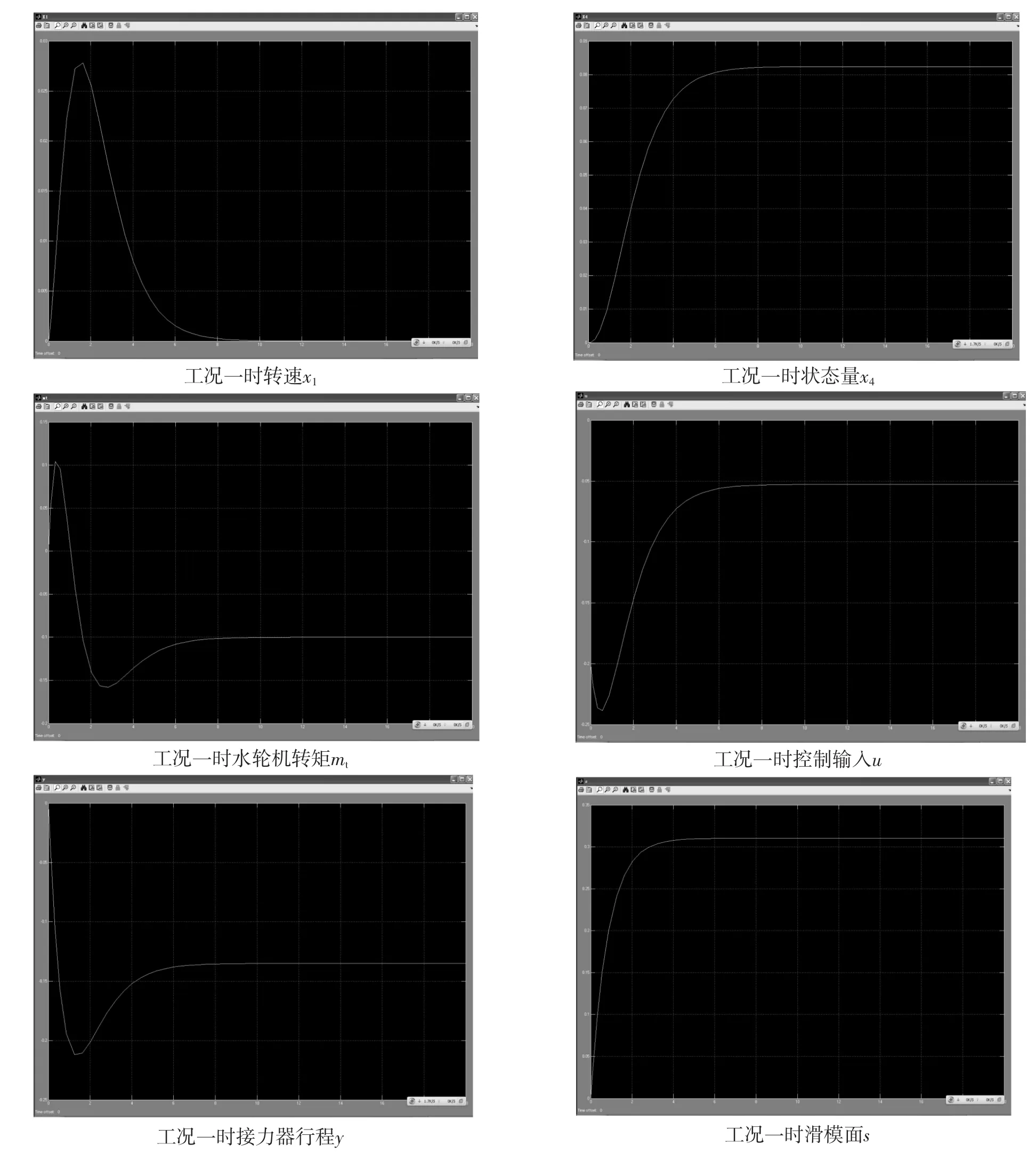
图4 工况一：负载扰动为10%时曲线

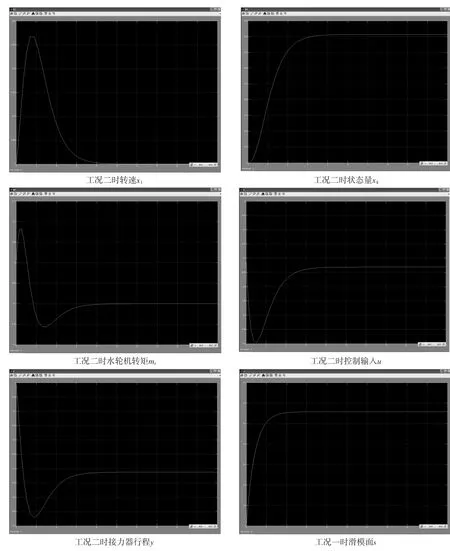
图5 工况二：负载扰动为10%时曲线

6 结论

本文提出一种基于滑模控制的水轮机调速方法,并利用模糊控制系统对滑模控制引起的“抖振”问题进行了探讨。通过对某一水电站水轮机在两种不同工况时的数据进行Matlab仿真,结果表明该方法在水轮机调速控制方面的可行性，且具有鲁棒性。

［1] H Q Fang，L Chen，N Dlakavu，Z Y Shen.Basic Modeling and Simulation Tool for Analysis of Hydraulic Transients in Hydroelectric Power Plants［J] .IEEE Transactions on Energy Conversion，2008，23（3）：834－841.

［2] 沈祖诒.水轮机调节［M] .北京：中国水利水电出版社，2001.

［3] Jones D，Mansoor S.Predicttive Feedforward Control for a Hydroelectric Plant［J] .IEEE Transactionns on Control Systems Technology，2004，12（6），956－965.

［4] 刘金琨.滑模变结构Matlab仿真［M] .北京：清华大学出版社，2005.

［5] 魏守平.现代水轮机调节技术［M] .武汉：华中科技大学出版社，2002.

［6] W Tan，Z Xu.Robust analysis and Design of Load Frequence Controller for Power Systems［J] .Electric Power Systems Research，2009，79（5）：846－853.

［7] 姚琼荟等.变结构控制系统［M] .重庆：重庆大学出版社，1997.