刀尖圆弧补偿在数控加工中的应用

2013-09-21王海港沈祥红

时代农机 2013年3期

关键词：假想车刀刀尖

王海港，沈祥红

（商丘职业技术学院，河南商丘 476000）

现代数控系统中，基本上通过刀具圆角半径补偿器来实现刀尖圆弧半径补偿的效果。对于此类的数控机床，编程人员可以具体根据零件轮廓形状进行变成。已达到在加工过程中，数控系统根据加工程序和刀具圆弧半径自动运算出的轨迹，进行刀具圆弧半径补偿。

1 运用刀尖圆弧补偿的原因

图1 刀具加工线路图

（1）对刀具进行产生误差的分析。如上图，编程数控机床在加工程序实行中，我们可以将车刀刀尖看成一个点。就像图1 a所表示的p点，p点是理论上的刀尖。但是我们在加工过程中，运用的车刀通常都是圆弧状的，像上图中的b，其主要是为了提高刀具使用寿命和降低加工工件的表面粗糙度，在实际应用中，刀尖磨成半径不大的圆弧（一般圆弧半径是在0.4-06），就像上图b中，X向与Z向的交点p称为理论刀尖（也名假想刀尖），这个点在编程的时候，是确定加工轨迹的点，是数控系统控制点的运行轨迹。但是在我们实际操作过程中，用于切削的点是A与B，很明显，假想的刀尖P点跟实际切削点A,B是不同的三个点。所以我们在机械数控加工过程中，必须对刀尖半径进行补偿，如果我们只是按照理论点进行加工编程，一定会造成加工误差。

（2）在加工过程中，刀尖圆弧半径对加工零件的影响。如上面所分析的，我们在理论上将刀尖看成一个点，但是车刀是有一点的弧度，现在我们在以一个连贯运行的图像进行分析车刀运行轨迹如上图。我们理论上把车刀当成一个点进行编程，然而在车削过程中，实际起到车削作用的是A与B点。因此在我们车削倒角，圆弧以及锥面时，会造成切削加工不到位的现象。

2 对于偏执刀具偏执值的计算

如图3 a所示，假想刀尖P点沿工件轮廓CD移动，如果按照轮廓线CD编程，用圆角车刀进行实际切削，必然产生CDD1 C1的残留误差。因此，实际加工时，圆头车刀的实际切削点要移至轮廓线CD，沿CD移动，如图3 b所示，这样才能消除残留高度。这时假想刀尖的轨迹C2 D2与轮廓线CD在X向相差ΔX，Z向相差ΔZ。设刀具的半径为r，可以求出：刀尖为C1和D1。对图4 a所示凸圆弧加工情况，圆弧C1D1为假想刀尖轨迹，O1点为圆心，半径为（R+r）；对图4 b所示凹圆弧加工情况，圆弧C2D2为假想刀尖轨迹，其圆心是O2点，半径为（R-r）。如果按假想刀尖轨迹编程，则要以图中所示的圆弧C1D1或C2D（2虚线）有关参数进行程序编制。

图2 刀尖欠切或过切过程

图3 车刀形状与位置示意图

图4

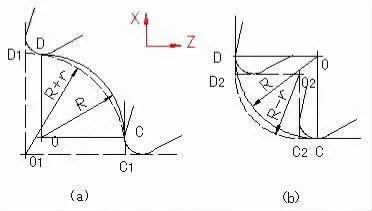
图5

3 刀尖圆弧半径补偿的方法

（1）在了解刀尖圆弧半径补偿的方法前，先要对补偿方法进行判定。在应用中，我们通常采用的是右手笛卡尔直角坐标系判断出第三根轴的正方向。沿着刀具的移动的方向看，刀具在工作轮廓左侧，是左补偿。反之，就是右补偿。但是也有刀具半径补偿去取消的，即使用此指令后，其他指令无效，并且值得注意的是，数控车床存在前置刀架以及后置刀架两种情况。但是刀具半径的补偿是一个样子的。

（2）刀具圆弧半径补偿的编程规则。在经用数控机床加工零部件时，为了保证生产质量与精度，编程中使用刀尖圆弧半径补偿方法下面是我们经常用到的一些规则①G40，G41，G42只能与G00以及G11结合进行编程，不能与G02G 03等其他指令结合编程。②在先编入程序G40，G41，G42与G00程序以及程序 G40，G41，G42以及程序G 01相结合的编程中，X，Z值至少得有一个值是变化的。③在进行刀具补偿的时候，要按照零部件的实际轮廓编写精加工轨迹。

4 刀具圆弧半径补偿在加工中的巧妙应用

在程序的设计中，要注意到刀尖圆弧半径补偿，在实际中，也要注意把刀尖半径以及刀尖的相应方位号输入到刀补之中，这个样子，工件加工时才不会出现明显误差。对于不具备补偿功能经济型数控系统的车床可直接按照假想刀尖的轨迹进行编程，即在编程时给出假想刀尖的轨迹，如图3 b和图4所示的虚线轨迹进行编程。如果采用手工编程计算相当复杂，通常可利用计算机绘图软件（如Auto CAD、CAXA电子图版等）先画出工件轮廓，再根据刀尖圆角半径大小绘制相应假想刀尖轨迹，通过软件查出有关点的坐标来进行编程；对于较复杂的工件也可以利用计算机辅助编程（CAM），编程时考虑半径补偿和由机床进行半径补偿，对于有些不具备补偿功能数控系统应该采用编程时考虑半径补偿，根据给出的刀尖半径和零件轮廓会自动计算出假想刀尖轨迹，通过软件后置处理生成假想刀尖轨迹的加工程序。