基于双矩形海湾模型的泰国湾潮汐潮流研究＊

吴 頔，方国洪＊，滕 飞，崔欣梅

（1.国家海洋局 第一海洋研究所，山东 青岛266061；2.海洋环境科学和数值模拟国家海洋局重点实验室，山东 青岛266061）

1920年，Taylor将等深矩形海湾里的潮波，分解为入射和反射的Kelvin波以及一族Poincaré波［1］（称为Taylor问题［2］），此后众多学者在此基础上进行研究和推广。Godin［3-4］将几个“Taylor模型”组合并考虑开边界强迫。陈宗镛［5］、方国洪和王仁树［6］、Rienecker和 Teubner［7］以及赵进平和侍茂崇［8］在经典 Taylor模型的基础上引入摩擦项，考虑了能量耗散问题。1973年，Brown［9］成功地采用了Defant的配置法［10］，克服了Kelvin波不完全反射时求解困难的问题，同时也使配置法成为拓展Taylor问题的有力工具，为后续的许多研究者沿用。但上面的研究只适用于半无限长海区。1991年，Fang等［11］将方国洪和王仁树的解［6］加以拓展，考虑了湾口处的强迫边界条件，给出适用于有限区域、包含摩擦效应的Taylor问题通解，进一步推广了 Taylor解析模型适应的范围。之后 Xia等［12］，Carbaijal［13］，Rizal［14-15］，Molen等［16］，Kagan等［17］，Roos和Schuttelaats［18-19］均针对不同海区采用有限区域的Taylor问题解进行研究。夏综万［20］对Taylor问题作出系统论述。

这些研究，除Rizal［15］外，都主要关注于中高纬度海域，所得潮波系统在北半球均为逆时针旋转的系统。位于9°N左右的泰国湾，其科氏参量远小于M2潮波角频率，存在一个顺时针旋转的M2潮波系统，特别值得予以理论上的解释。我们以Fang等［11］的模型为基础，建立了一个双矩形的海湾模型，以研究泰国湾的潮波问题。该模型不但考虑了摩擦耗散和开边界强迫，其双矩形结构囊括泰国湾中的曼谷湾区域，使得模拟结果更接近真实。

1 模型的设置与求解

1.1 模型设置

新建立的双矩形海湾模型由2个不等深矩形海湾组成（图1），左右2个矩形区域分别称为区域一和区域二。每个区域独立满足如下假设：1）摩擦力与流速的一次方成比例；2）科氏参量在海湾内为一常数；3）不计作用于海水质量上的引潮力；4）直线表示壁面，其法向速度为0；开边界（图1中x=0处虚线）存在外海输入潮波强迫。

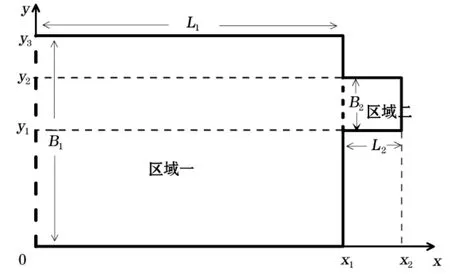
图1 双矩形海湾模型Fig.1 A sketch map of the two-rectangular-gulf model

假设区域一和区域二的水深均为常数，记为h1和h2；2个区域长度分别为L1和L2；宽度分别为B1和B2。区域一的范围在x方向从0到x1（x1=L1），在y方向从0到y3（y3=B1）；区域二的范围在x方向从x1到x2（x2=L1+L2），在y方向从y1到y2（y2=y1+B2）。

1.2 控制方程和边界条件

取潮波运动方程和连续方程：

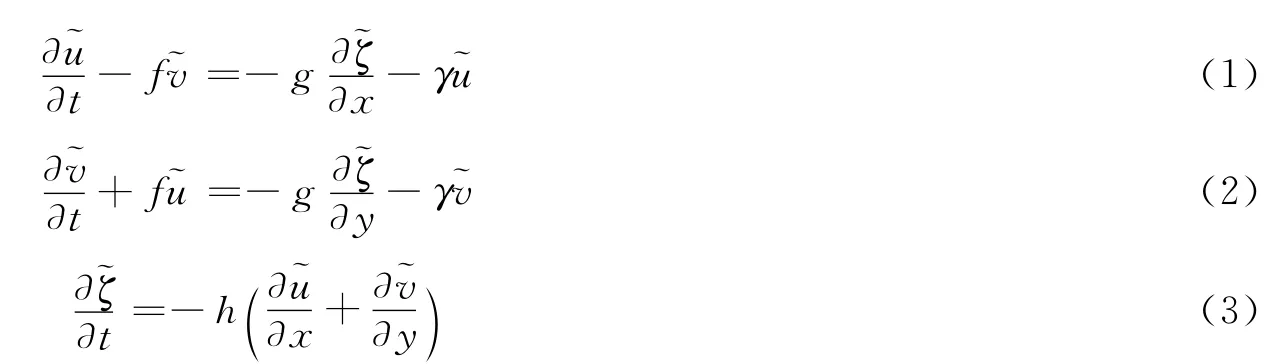
其中分别为x，y方向潮流流速为从海平面算的潮位高度；f=2Ωsinφ为科氏参数，其中Ω（7.29×10-5s-1）为地转角速率，φ为纬度；γ，h和g分别为摩擦系数、海区水深和重力加速度。将2个区域的潮位高度及流速分别表示为（j=1时，0≤x≤x1；j=2时，x1≤x≤x2），且满足式式（1）～式（3）。边界条件：

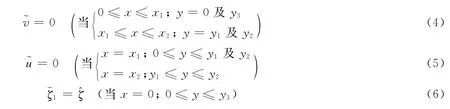
其中）为x=0处水位，即开边界强迫。衔接条件：

式（7）保证了2个区域的潮波在连接处水位、体积输运及能通量的连续性。

设和eiσt成比例，即存在使得：

则式（1）～式（3）可改写：

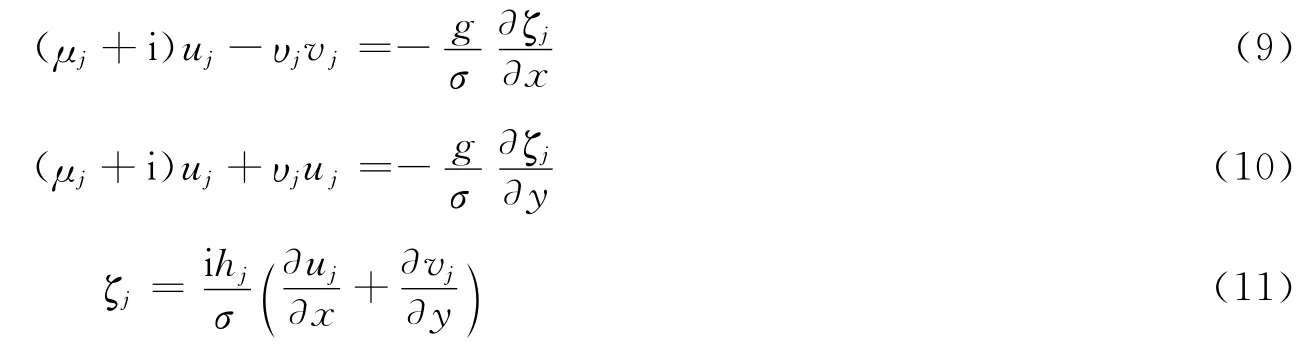
其中，

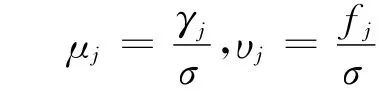
又由式（9）～式（11）计算得出：

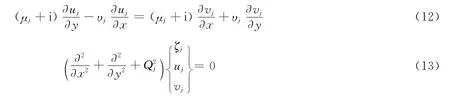
其中，

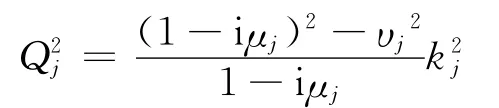
kj=σ／cj为Kelvin波的波数为重力长波的相速度。

相应的边界条件式（4）～式（6）改写：

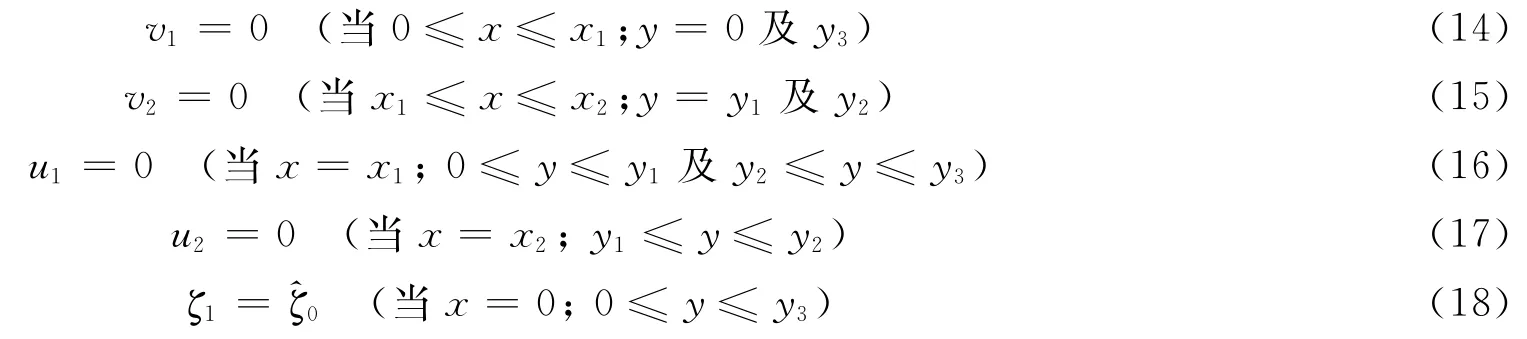
其中，Z0和θ0为开边界处水位的振幅和迟角。

衔接条件：

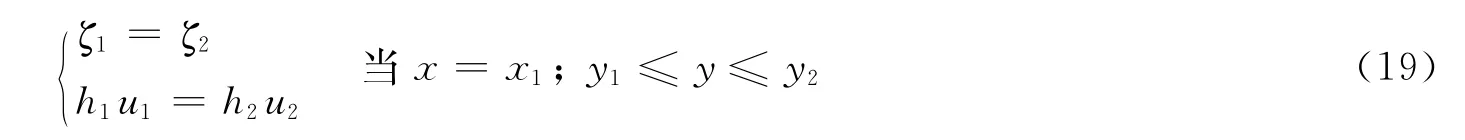
1.3 方程解法

1.3.1 方程的通解

根据式（14）和（15）的条件，可以给出满足方程的四族Kelvin波式（20）～式（23）和四族Poincaré波式（24）～式（27）：

其中，。sj，n取实部为正的值。将以上代入式（13）可以推出：

式（20）～式（27）中aj，bj，κj，n和λj，n为待定常数，需通过下列关系计算。将式（20）～式（27）代入式（16）～式（19），则壁面条件式（16）和（17）改写：

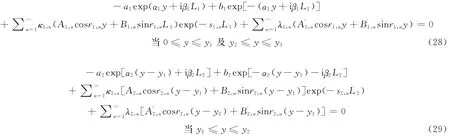
开边界条件式（18）改写：

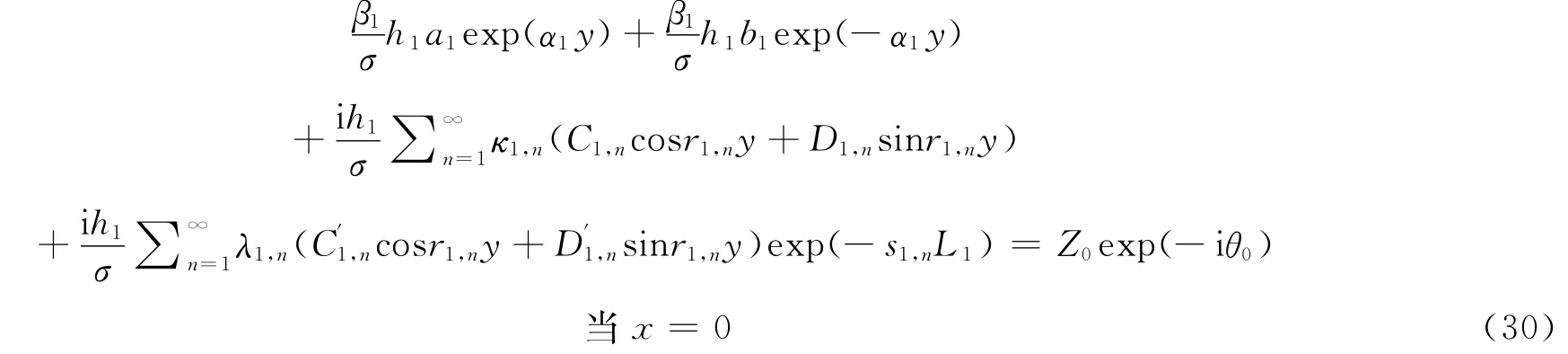
衔接条件式（19）改写：

1.3.2 配置法

采用配置法求方程组的近似解。先将式（24）和（26）所示的Poincaré波族截断至N1阶，在x=0，0≤y≤y3和x=x1，0≤y≤y3两条线段上均匀取2 N1+2个点。设线段x=x1，y1≤y≤y2上取了J=N2+1个点，则在线段x=x2，y1≤y≤y2上对应取N2+1个点。将这2 N1+N2+3个点坐标代入边界条件式（28）～（32）中可得2 N1+2 N2+4个方程，不难解出aj，bj，kj，nj和λj，nj（nj=1，2，…，Nj；j=1，2）。

2 双矩形模型在泰国湾中的应用

泰国湾介于中南半岛和马来半岛之间（图2）。地理范围为99°10′～105°00′E，6°00′～13°30′N，湾口向东南开，西北端深入的湄南河口部分称为曼谷湾。

由于泰国湾处于低纬度地区，受弱科氏加速度的影响，其潮波系统相对复杂，尤其是频率较大的半日潮。以M2分潮为例，其泰国湾湾口的顺指针旋转的无潮点有悖于北半球的一般规律，一直受到相关学者的关注，而其泰国湾湾顶无潮点的存在性及位置，直至今日各学者给出的结果仍不尽相同。

在1944年Dietrich就给出基本不反映泰国湾潮波主要结构的同潮图。后来 Defant［10］、Ye和 Robinson［21］、俞慕耕［22］给出的同潮图，虽结果有所改善，但相互之间的差异十分显著。此后，丁文兰［23］、Fang［24］、Yanagi和 Toshiyuki［25］、Fang等［26］、Zu等［27］均给出了泰国湾的同潮图。其中 M2分潮在泰国湾湾口的无潮点基本确定，但湾顶无潮点的存在及位置依旧不尽相同。上述研究方法均局限于资料分析和数值模拟，未给出理论解释。

此外，由于曼谷湾的存在，使得单一矩形区域的Taylor模型不足以刻画泰国湾的潮汐分布。借助新建立的双矩形海湾模型来模拟该区域K1和M2分潮的潮波系统，并针对M2分潮的影响因素，包括曼谷湾和开边界条件，进行了相关实验研究。

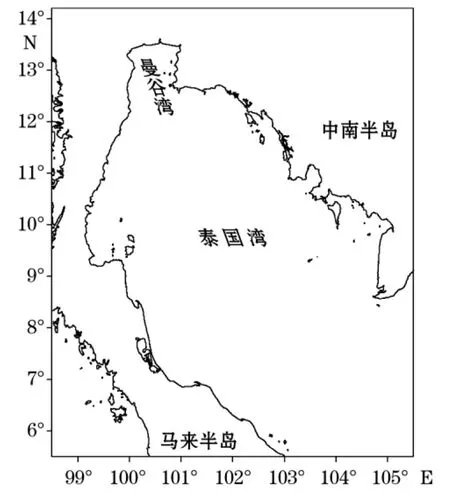
图2 泰国湾示意图Fig.2 A sketch map of the Gulf of Thailand

2.1 模型设置

取L1=580 mm，B1=400 km，h1=40 m，L2=110 km，B2=100 km，y1=220 km，h2=13 m。这些数值使模型等效于泰国湾，其中区域一代表泰国湾主体，区域二代表曼古湾。并取N1=19，N2=5，在线段x=0，0≤y≤y3和线段x=x1，0≤y≤y3上均匀各取20个配置点，在线段x=x2，y1≤y≤y2，上均匀取5个点（图3）。对 K1和 M2分潮，σ分别取7.286 7×10-5s-1、1.405 2×10-4s-1。μj则仿照Fang等［11］中所给量级取0.1。根据泰国湾及曼谷湾所处纬度，取科氏参数f1=0.22×10-4s-1；f2=0.33×10-4s-1。开边界条件的调和常数采用Fang等［26］数值模拟结果（采用东8时区迟角）。

采用1.3.2节中方法解出相关参数出aj，bj，kj，nj和λj，nj（nj=1，2，…，Nj；j=1，2），代入式（20）～式（27）即可解出对应分潮的ζj，uj，vj。根据式（8）引入时间因子eiσt之后取实部可得：

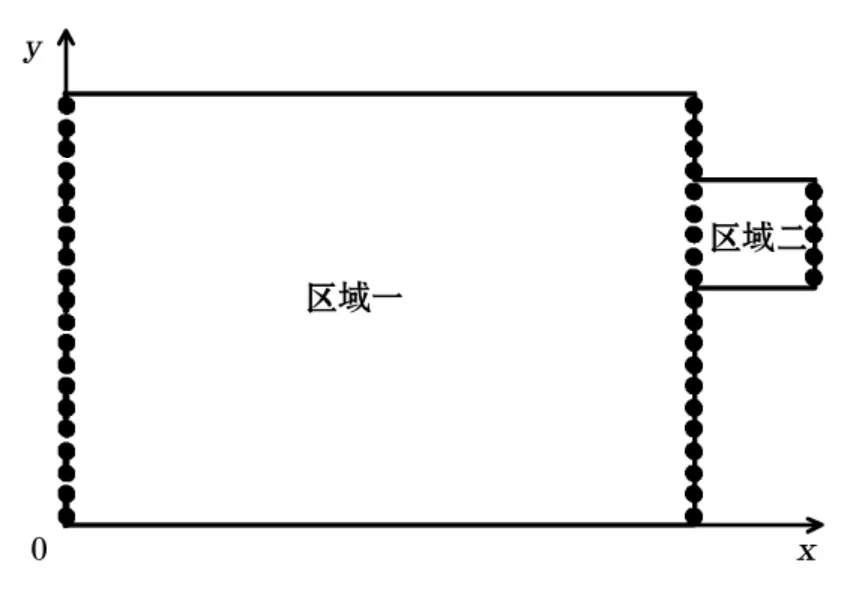
图3 配置点示意图Fig.3 Setting up the Collocation points

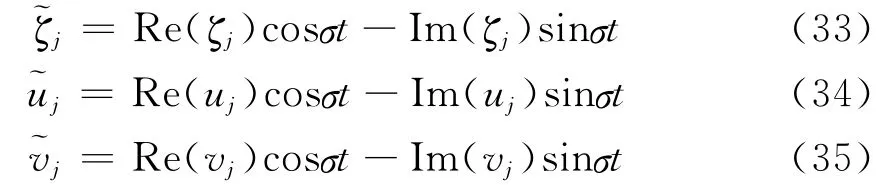
为研究海湾模型的潮汐分布，利用式（33）导出相应分潮迟角θj及振幅Zj关系式：

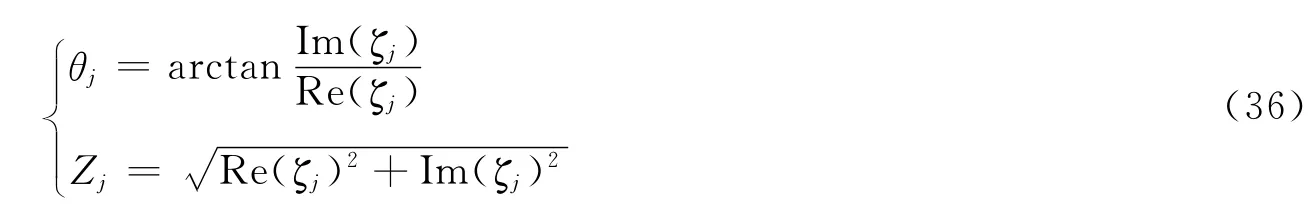
2.2 潮汐分布

根据上述方法得到泰国湾-曼谷湾理论解（图4a和图5a）；使用文献［26］数据重绘同潮图（图5a和图5b）。其中K1分潮结构较为简单，图4a和图4b中潮汐分布格局一致。在泰国湾中存在一逆时针旋转的无潮点，其位置偏向湾口，并向西岸偏移。振幅则随着向湾顶的深入而不断加大，最大振幅出现在曼谷湾湾顶。

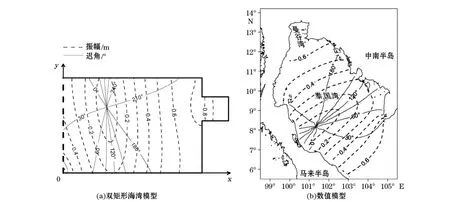
图4 K1分潮同潮图Fig.4 Co-tidal chart of tidal constituent K1

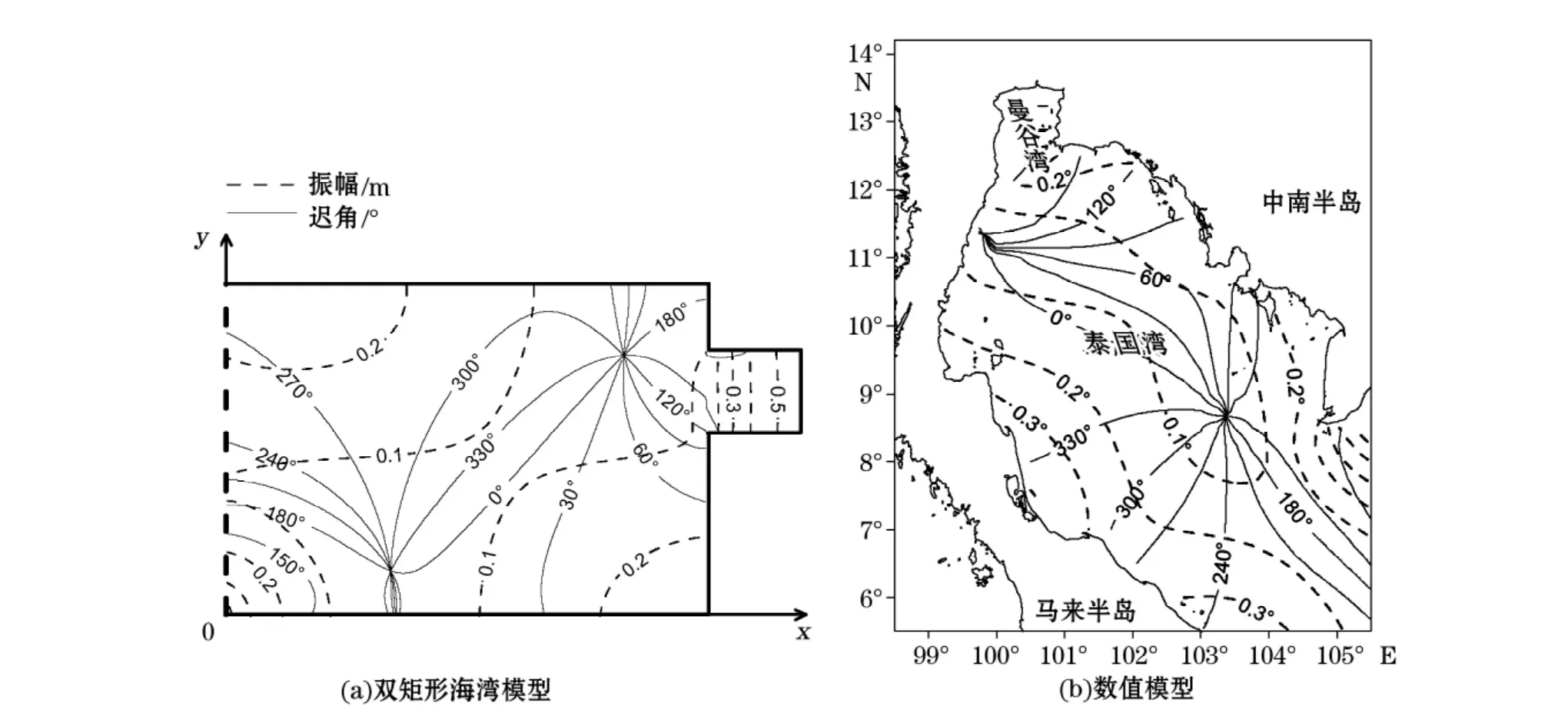
图5 M2分潮同潮图Fig.5 Co-tidal chart of tidal constituent M2

M2分潮频率大，波长仅为K1分潮的一半，故潮波结构比K1分潮复杂的多。图5a中显示，M2分潮振幅在泰国湾（除曼谷湾部分）较小，最大振幅不超过0.3 m，在曼谷湾中向湾顶方向不断增大；迟角分布则较复杂，出现2个无潮点。其中一个无潮点位于泰国湾湾顶、曼谷湾口外，呈逆时针旋转。另一个无潮点则靠近泰国湾湾口，偏向东岸，呈顺时针旋转，该无潮点不遵循北半球潮波逆时针旋转的一般规律。对比图5a和图5b，M2分潮振幅分布格局一致。

为分析K1和M2分潮的构成，分别给出这2个分潮在区域一中的Kelvin波和Poincaré波分布（图6和图7）。由图6中可以看出K1分潮潮波由于其频率小、波长长，虽然处于较低纬度的泰国湾区域，其组成仍然以Kelvin波为主，并表现出明显的Kelvin波性质。Kelvin波受北半球向右的科氏加速度影响，入射波东岸强西岸弱，反射波东岸弱西岸弱。合成结果构成了一个逆时针旋转的潮波系统。由于模型考虑了摩擦，潮波在传播过程中产生能量耗散，使得反射波的能量小于入射波，总的叠加效果东岸强西岸弱，因此无潮点偏向西岸。

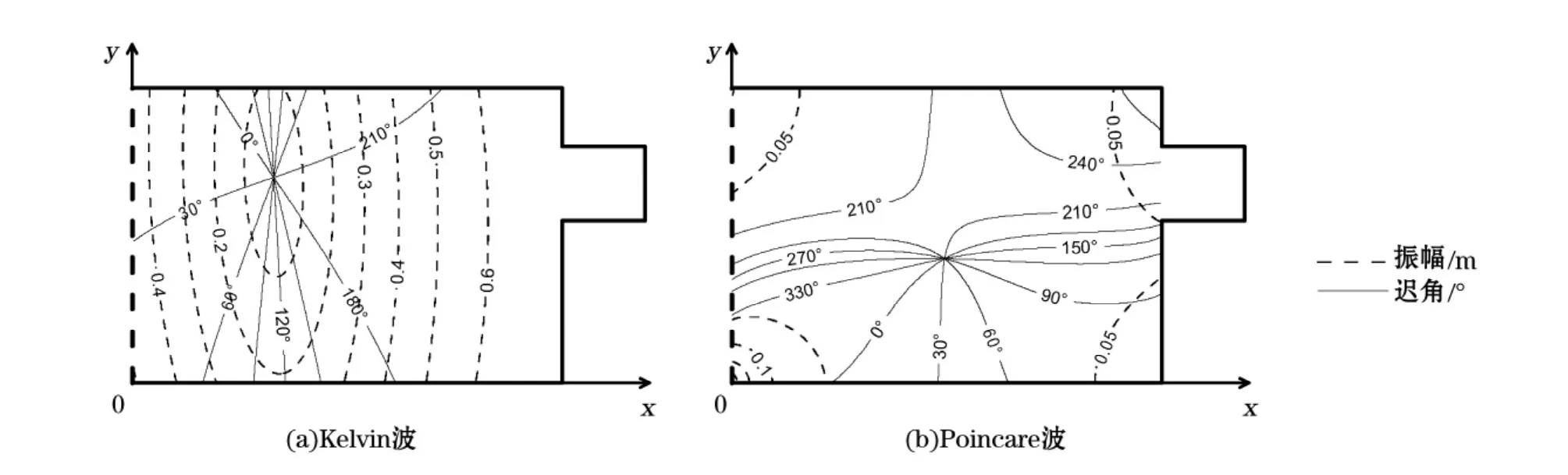
图6 K1分潮在区域一中的潮波分解Fig.6 Decomposition of K1 in area I

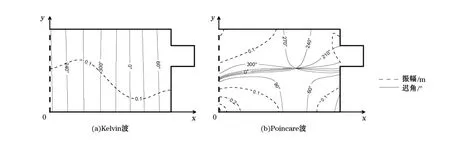
图7 M2分潮在区域一中的潮波分解Fig.7 Decomposition of M2 in area I

由M2分潮Kelvin波和Poincaré波的组成（图7）可见，M2分潮由于频率高，在低纬度区惯性频率f比潮波频率σ小很多，故在泰国湾区域Kelvin波较弱，且由于能量耗散，入射波远远强于反射波，没有叠加形成无潮点。而Poincaré波在泰国湾湾口较强，且存在一个逆时针旋转的无潮点。Kelvin波和Poincaré波叠加后在湾顶形成一逆时针旋转的无潮点，湾口形成一顺时针旋转的无潮点。

考虑到Poincaré波主要是受边界条件和衔接条件控制，我们认为除低科氏加速度及地形因素影响外，曼谷湾是影响泰国湾湾顶形成逆时针旋转的无潮点的重要因素；开边界条件是泰国湾湾口形成顺时针旋转的无潮点的首要因素。

2.3 潮流分布

为了研究泰国湾的潮流分布情况，根据2.1节中结果分别计算了K1和M2分潮的潮流椭圆要素（半长轴、半短轴、长轴倾角及迟角），并给出相应分潮的潮流椭圆（图8和图9）。

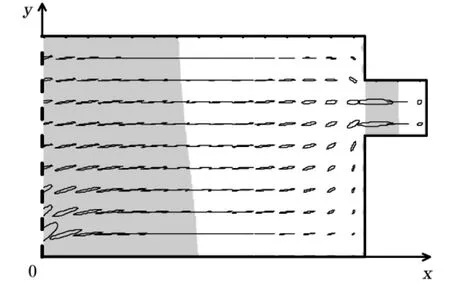
图8 K1分潮的潮流椭圆图（阴影表示顺时针旋转）Fig.8 K1 current ellipses（shaded part indicates clockwise rotation）

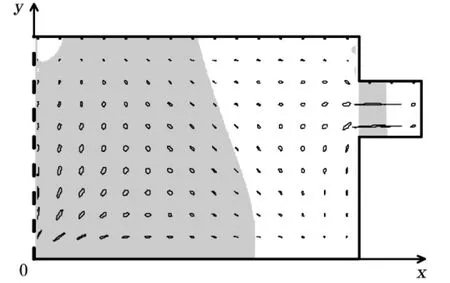
图9 M2分潮的潮流椭圆图（阴影表示顺时针旋转）Fig.9 M2 current ellipses（shaded part indicates clockwise rotation）

K1分潮潮流在区域一中主要呈逆时针旋转，在区域二中主要呈顺时针旋转，在2个区域内均以往复流为主。泰国湾湾口东侧和曼谷湾湾口东侧出现较大流速。在泰国湾腹部，长轴平行于x轴，在湾顶则逐渐垂直于x轴，在与Taylor［1］给出的等深矩形海湾十分相似。

M2分潮潮流在泰国湾和曼谷湾的湾口附近都呈顺时针旋转，在2个海湾的湾顶附近则都呈现逆时针旋转，与Fang等的理论分析［11］一致。

2.4 潮能通量

潮能通量强度又叫做能通量密度，表示单位时间内通过单位宽度的垂直断面的潮波能量，其计算公式：

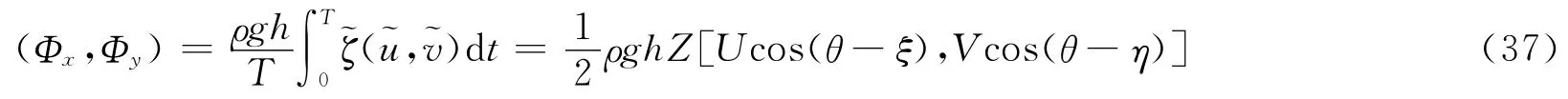
式中（Φx，Φy）为能通量密度在（x，y）方向的分量；T 为潮波周期；ρ为海水密度，取1 025 kg／m3；Z 和θ分别为潮汐的振幅和迟角；（U，V）为（x，y）方向潮流分量的振幅，（ξ，η）为相应的迟角。

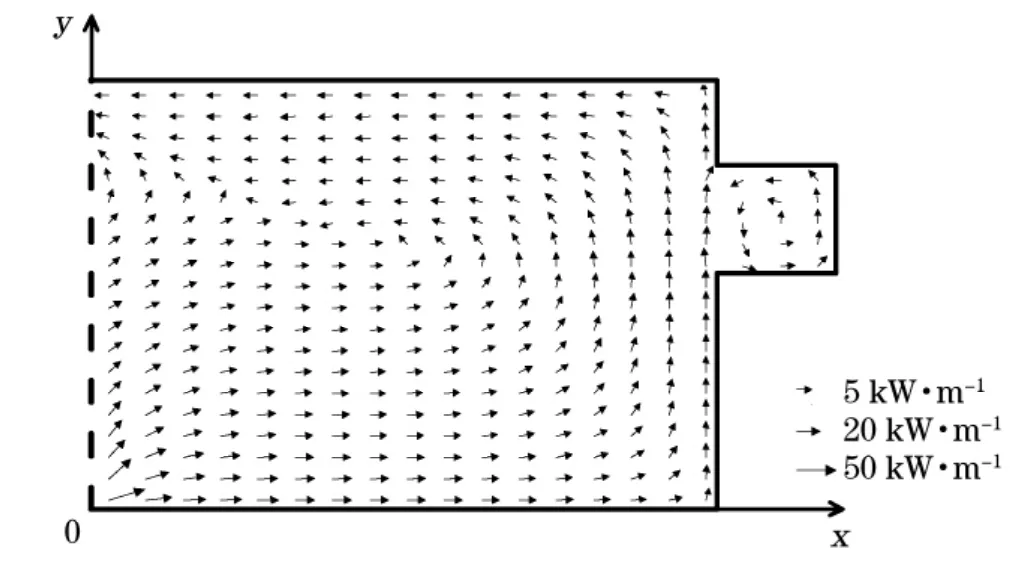
图10 K1分潮能通量密度分布图Fig.10 The tidal energy flux density vectors of constituent K1

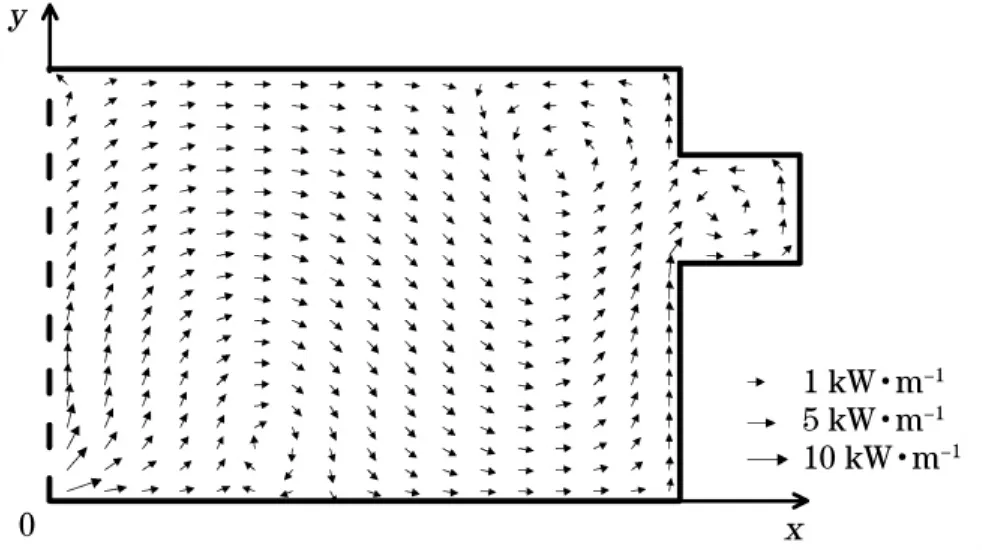
图11 M2分潮能通量密度分布图Fig.11 The tidal energy flux density vectors of constituent M2

根据式（37）及前文结果，计算了K1和M2分潮的潮能通量密度，并绘制潮能通量密度分布图以刻画K1和M2分潮能通量流向（图10和图11）。图10中K1分潮能量从东岸输入，并沿东岸向湾顶传输，自东向西扫过湾顶，并沿西岸输出，在传输过程中，能量逐渐减弱。这体现出Kelvin波在北半球传播的一般规律。图11中M2分潮能量较小，正如2.2节所述，受开边界及弱科氏加速度影响，其能量从东岸输入，但直接流向西岸，且沿西岸传输，缓慢右转，转向东岸后，沿东岸传输直至湾顶，后沿湾顶边界自东向西传输，在曼谷湾处分为2支，一部分流入曼谷湾，另一部分继续沿湾顶传输。

3 敏感性实验

曼谷湾对M2分潮在泰国湾湾顶形成逆时针旋转的无潮点起重要作用；开边界条件是M2分潮在泰国湾湾口形成顺时针旋转的无潮点的必要条件。为了验证上述观点，我们设计了如下2组实验：1）曼谷湾实验：删除代表曼谷湾的区域二，其他条件同2.1节；改变区域二位置，其他条件同2.1节。2）开边界实验：开边界条件采用等振幅边界，其他条件同2.1节；开边界条件采用等迟角边界，其他条件同2.1节。

3.1 曼谷湾存在和位置的敏感性实验

针对M2分潮，改变曼谷湾的存在及位置，控制其他条件与2.1节中一致，以探讨曼谷湾对泰国湾M2分潮的影响。

方案1 只保留区域一，即建立一个单一矩形海湾模型（图12），其他条件保持与2.1节相同，以此排除曼谷湾的影响。实际计算中在模型两端均匀各取20个配置点（图12a），沿用Fang等的解法［11］，计算该矩形海湾模型的潮汐分布，得到M2分潮的同潮图如图12b所示。

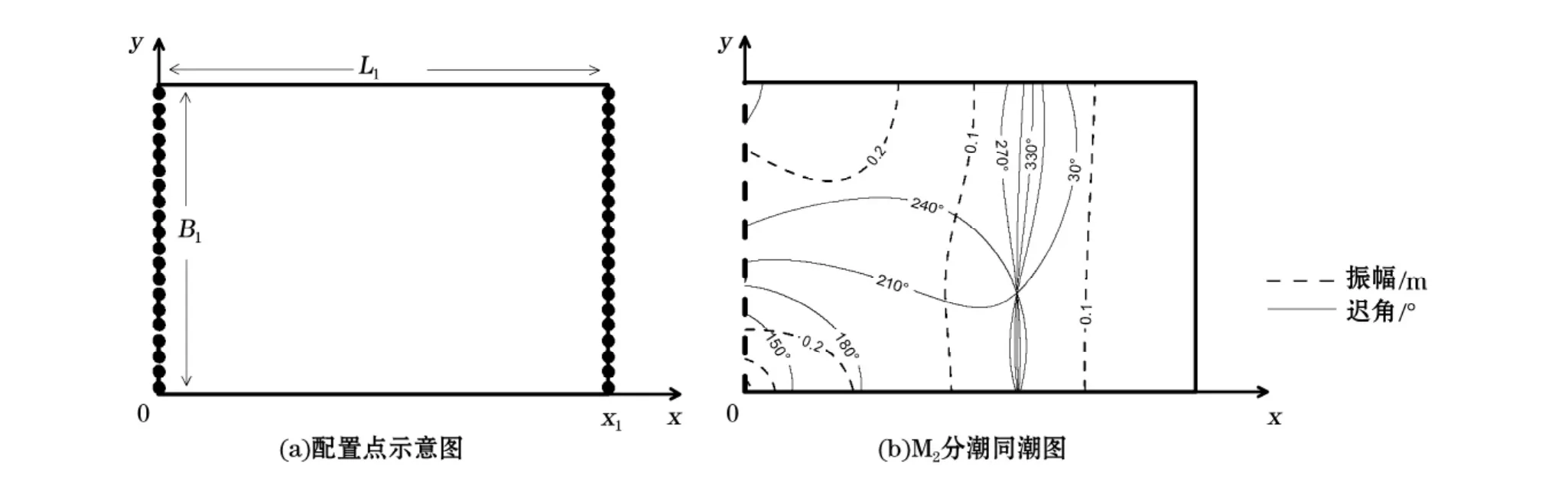
图12 泰国湾的矩形海湾模型Fig.12 A single-rectangular-gulf model for the Gulf of Thailand

对比图12b与图5a结果可见，M2分潮在泰国湾仍然存在一顺时针旋转的无潮点，但其位置向湾内深入，而湾顶逆时针旋转的无潮点完全消失。

方案2 令y1=160 km；其他条件同2.1节。

方案3 令y1=100 km；其他条件同2.1节。

方案2和3的结果分别示于图13。对比图13与图5a结果可知，随着曼谷湾向东平移，M2分潮在泰国湾湾口顺时针旋转的无潮点位置变化不大，湾顶的无潮点向湾顶方向发生退化，但可以看出这个无潮点随曼谷湾位置东移向东北移动。

综合上述3个方案，可以看出曼谷湾是影响M2分潮在泰国湾湾顶形成逆时针旋转的无潮点的重要因素，其存在促使M2分潮在泰国湾湾顶形成无潮点，且曼谷湾的位置决定了该无潮点的位置。

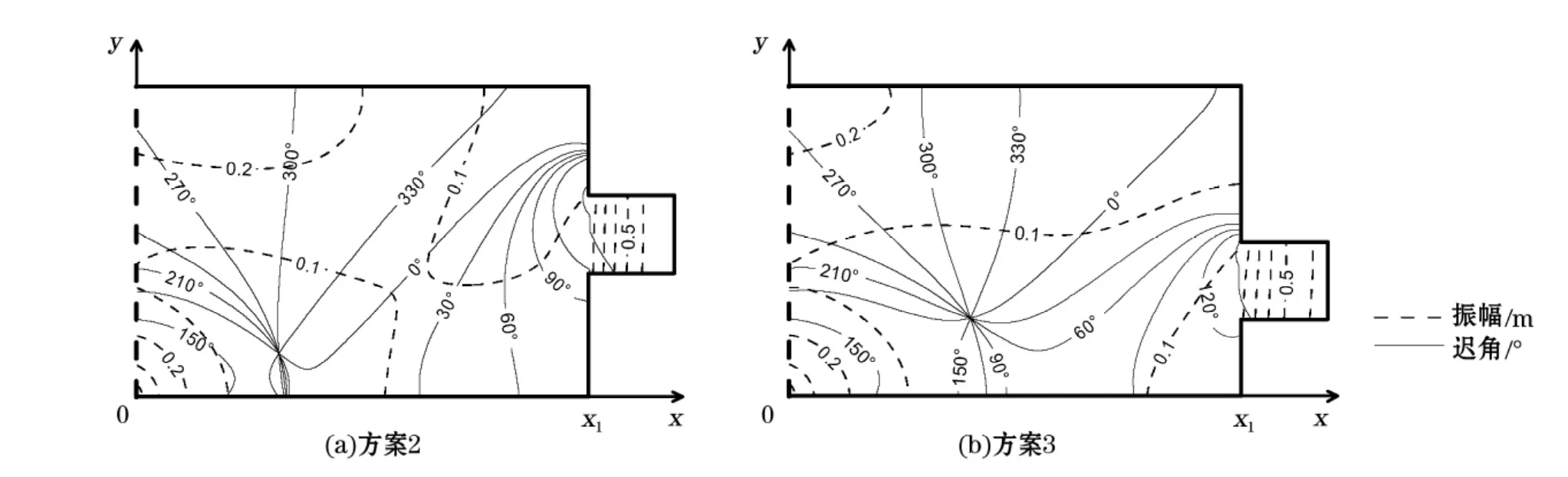
图13 曼谷湾实验的M2分潮同潮图Fig.13 The co-tidal chart of M 2 resulted from the sensitive experiments in the Gulf of Bangkok

3.2 开边界条件的敏感性实验

着眼于研究泰国湾M2分潮对开边界的响应，具体方案：

方案1 开边界振幅均取0.2 m，其他条件同2.1节；

方案2 开边界迟角均取0°，其他条件同2.1节。

依旧采用2.1节中的方法，分别计算方案1、方案2模型的潮汐分布，并给出相应同潮图（图14）。

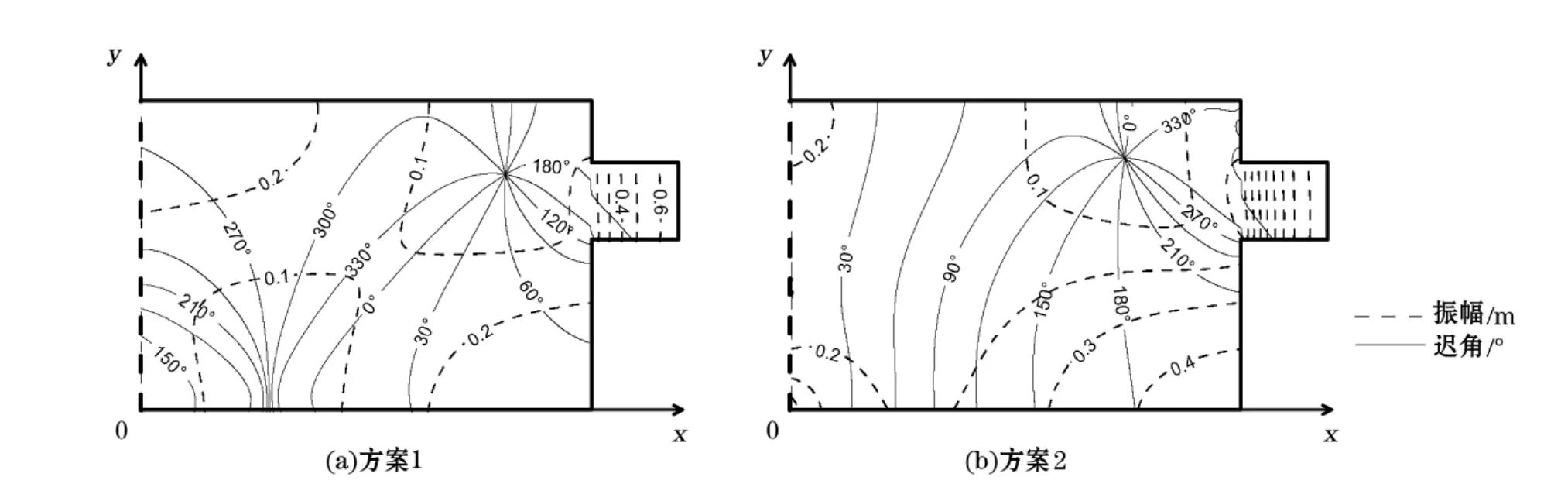
图14 开边界实验的M2分潮同潮图Fig.14 The co-tidal chart of M2 resulted from the sensitive experiments under the open boundary condition

与图5a结果比较可见，当开边界振幅为常数时，其振幅结构变化不大，湾口的无潮点退化至东岸，但依然保持顺时针旋转的结构。当开边界迟角给定均匀值时，湾口顺时针的无潮点完全消失，潮波进入海湾后差不多以前进波的形式向湾顶推进，并在曼谷湾湾口外形成一个逆时针旋转的无潮点。对比2组实验结果，不难看出，改变开边界条件不影响湾顶形成逆时针的无潮点；而M2分潮在泰国湾湾口顺时针旋转的无潮点，主要依赖于开边界迟角自东向西增加的梯度条件，即潮波传入泰国湾的方向；而湾口的振幅变化对该无潮点形成仅起到加强作用。迟角自东向西的增加则是南海M2分潮潮波自东北向西南传播的结果。

5 结 语

本文利用双矩形海湾模型研究了泰国湾的潮波问题。研究表明：

1）K1分潮潮波在泰国湾中主要表现Kelvin波的性质；

2）M2分潮在泰国湾中Kelvin波的性质较弱，湾口和湾顶主要受Poincaré波控制；

3）曼谷湾的存在是M2分潮在泰国湾湾顶形成逆时针旋转无潮点的主要原因，其位置决定了该无潮点的位置；

4）开边界迟角自东向西增加的梯度条件是M2分潮在泰国湾湾口顺时针无潮点形成的必要条件。

：

［1］ TAYLOR G I.Tidal oscillations in gulfs and rectangular basins［J］.Proc.Lond.Math.Soc.，1922，s2-20（1）：148-181.

［2］ HENDERSHOTT M C，SPERANZA A.Co-oscillating tides in long，narrow bays：the Taylor problem revisited［J］.Deep Sea Research and Oceanographic Abstracts，1971，18（10）：959-980.

［3］ GODIN G.Some remarks on the tidal motion in a narrow rectangular sea of constant depth［J］.Deep Sea Research and Oceanographic Abstracts，1965，12（4）：461-468.

［4］ GODIN G.The M2tide in the Labrador Sea，Davis Strait and Baffin Bay［J］.Deep Sea Research and Oceanographic Abstracts，1965，12（4）：469-477.

［5］ CHEN Z Y.A tidal mode of rectangular shallow basins［J］.Oceanologia et Limnologia Sinica，1965，7（2）：85-93.陈宗镛.长方形浅水海湾的一种潮波模式［J］.海洋与湖沼，1965，7（2）：85-93.

［6］ FANG G H，WANG R S.Tides and tidal streams in gulfs［J］.Oceanologia et Limnologia Sinica，1966，8（1）：60-77.方国洪，王仁树.海湾的潮汐与潮流［J］.海洋与湖沼，1966，8（1）：60-77.

［7］ RIENECKER M M，TEUBNER M D.A note on frictional effects in Taylor's problem［J］.Journal of Marine Research，1980，38（2）：183-191.

［8］ ZHAO J P，SHI M C.The tidal wave reflection problem and the influence of friction in Semi-enclosed rectangular basin［J］.Acta Oceanologica Sinica，1988，10（3）：259-269.赵进平，侍茂崇.半封闭矩形海湾中潮波反射问题及摩擦的影响［J］.海洋学报，1988，10（3）：259-269.

［9］ BROWN P J.Kelvin wave reflection in a semi-infinite canal［J］.Journal of Marine Research，1973，31（1）：1-10.

［10］ DEFANT A.Physical Oceanography［M］.New York：Pergamon Press，1961：590.

［11］ FANG Z，YE A L，FANG G H.Solutions of tidal motions in a semi-closed rectangular gulf with open boundary condition specified［M］∥Tidal Hydrodynamics，New York：John Wiley &Sons Inc.，1991：153-168.

［12］ XIA Z W，CARBAJAL N，SUNDERMANN J.Tidal current amphidromic system in semi-enclosed basins［J］.Continental Shelf Research，1995，15（2-3）：219-240.

［13］ CARBAJAL N.Two applications of Taylor's problem solution for finite rectangular semi-enclosed basins［J］.Continental Shelf Research，1997，17（7）：803-817.

［14］ RIZAL S.The role of non-linear terms in the shallow water equation with the application in three-dimensional tidal model of the Malacca Strait and Taylor's Problem in low geographical latitude［J］.Continental Shelf Research，2000，20（15）：1965-1991.

［15］ RIZAL S.Taylor's problem-influences on the spatial distribution of real and virtual amphidromes［J］.Continental Shelf Research，2002，22（15）：2147-2158.

［16］ MOLEN J，GERRITS J，SWART H E.Modelling the morphodynamics of a tidal shelf sea［J］.Continental Shelf Research，2004，24（4-5）：483-507.

［17］ KAGAN B A，ROMANENKOV D A.Effect of hydrodynamic properties of the sea bottom on the tidal dynamics in a rectangular basin［J］.Atmospheric and Oceanic Physics，2006，42（6）：777-784.

［18］ ROOS P C，SCHUTTELAATS H M.Horizontally viscous effects in a tidal basin：extending Taylor's problem［J］.Journal of Fluid Mechanics，2009，640：421-439.

［19］ ROOS P C，SCHUTTELAATS H M.Influence of topography on tide propagation and amplification in semi-enclosed basins［J］.Ocean Dynamics，2011，61（1）：21-38.

［20］ XIA Z W.Taylor problem of tidal wave［M］.Beijing：Ocean Press，2011.夏综万.海洋潮波的Taylor问题［M］.北京：海洋出版社，2011.

［21］ YE A L，ROBINSON I S.Tidal dynamics in the South China Sea［J］.Geophysical Journal of the Royal Astronomical Society，1983，72（3）：691-707.

［22］ YU M G.Preliminary discussion on tidal characteristic of South China Sea［J］.Acta Oceanologica Sinica，1984，6（3）：293-300.俞慕耕.南海潮汐特征的初步探讨［J］.海洋学报，1984，6（3）：293-300.

［23］ DING W L.Distribution of tides and tidal currents in the South China Sea［J］.Oceanologia et Limnologia Sinica，1986，17（6）：468-480.丁文兰.南海潮汐和潮流的分布特征［J］.海洋与湖沼，1986，17（6）：468-480.

［24］ FANG G H.Tide and tidal current charts for the marginal seas adjacent to China［J］.Chinese Journal of Oceanology and Limnology，1986，4（1）：1-16.

［25］ YANAGI T，TOSHIYUKI T.Clockwise phase propagation of semi-diurnal tides in the Gulf of Thailand［J］.Journal of Oceanography，1998，54（2）：143-150.

［26］ FANG G H，KWOK Y K，YU K J，et al.Numerical simulation of principal tidal constituents in the South China Sea，Gulf of Tonkin and Gulf of Thailand［J］.Continental Shelf Research，1999，19（7）：845-869.

［27］ ZU T T，GAN J P，EROFEEVA S Y.Numerical study of the tide and tidal dynamics in the South China Sea［J］.Deep Sea Research Part I：Oceanographic Research Papers，2008，55（2）：137-154.