基于模糊神经网络的自动冲床送料系统摩擦力自适应控制研究

徐立军，何颖，王维庆

（新疆工程学院，电气与信息工程系，乌鲁木齐 新疆 830091）

0 引言

针对变压器专用绝缘条形材料的冲裁问题，项目组设计了一套专用的自动冲床，该冲床的关键技术为依靠滚轮摩擦力送料的自动送料系统的自动控制，要求在加工对象表面摩擦力随机变化的情况下保持送料速度稳定。

加工过程中存在滚轮和加工材料之间的摩擦力及材料与导轨之间的摩擦力，其中材料与导轨在高速运动过程中产生的非线性摩擦力对系统的控制精度影响非常大，非线性的摩擦力导致整个控制对象的非线性，用传统的控制方法很难达到高精度的控制效果。解决这个问题的一个行之有效的办法是建立摩擦力的数学模型并在此基础上进行补偿控制，针对该类伺服系统人们已经提出了许多控制方法，如对偶自校正PID控制［1］、基于重复控制原理的动态补偿方法［2］、鲁棒自适应摩擦补偿法［3］、PID加迭代学习的复合控制方法［4］及速度鲁棒跟踪控制［5］等，以上控制方法在限定条件下可以获得较好的控制效果，但是在工程应用中缺乏广泛适用性，因为从控制应用角度来说，构建的摩擦力模型越简单越好，但如果只考虑静摩擦力（库伦摩擦）及粘性摩擦等因素，可能引起因误差过大导致的过补偿，从而产生极限环［6］。产生摩擦力的因素很多，摩擦力大小不仅与负载大小、接触位置及运动速度有关，而且受运动维持时间、环境温度、运动速度及接触位置等因素影响，诸多因素，导致摩擦力模型的非线性，因此，要获得其精确的数学模型非常困难。在具体应用环境下的控制策略只能考虑系统中影响摩擦力的主要因素，根据参数及环境因素的改变适时调节摩擦力模型［7］，可能导致模型的非通用型，同时，自适应控制算法的复杂性也限制了其实际工程应用。

神经网络能够以任意精度逼近任意L2范数上的非线性函数，并可以进行学习，以适应环境的变化，非常适合用来描述具有非线性特征的摩擦力模型，并便于用现有的计算机技术或超大规模集成电路（VLSI）实现［8］，从而具有广泛的工程应用基础。只需要选取合适的网络模型及训练方式就可以构成具有自学习自适应功能的模型，从而很好的对摩擦力进行补偿。

本文针对高速冲床摩擦力驱动系统，在讨论了摩擦力驱动模型的基础上，采用模糊控制与神经网络的结构等价方式，用多节点的网络来实现模糊映射，构成了一种但隐含层的三层模糊神经网络，用于直流伺服电机的控制，对电机单轴转动速率进行摩擦力自适应补偿研究，从而提高其控制精度。

1 摩擦力特性分析及建模

1.1 线性特性分析

影响摩擦力的线性因素主要为库伦摩擦/静摩擦、粘性摩擦力矩以及位置相关性等。

（1）库伦摩擦/静摩擦

当物体开始运动时，存在一阻止运动进行的恒值摩擦力，若外部作用力小于静摩擦力，运动速度就为零。其表达式为:

式中q为角度，a为库伦摩擦力矩。

（2）粘性摩擦力矩

该力矩与角速度成正比关系:

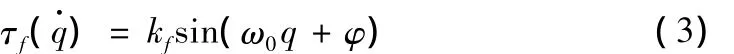
1.2 非线性特性分析

式中β为粘性摩擦力矩。

（3）位置相关性

在某些伺服系统中，传动与减速机构的误差可能会导致周期与减速比相对应的振荡，从而产生摩擦力变化［9］。

摩擦力的非线性特性主要表现为滑动粘附现象［10］、动态滞后效应［11］、Stribeck 效应［11］和可变最大静摩擦力［12］等，

（1）滑动粘附现象

对应于克服静摩擦力产生运动后，由接触面弹塑性变化引起的摩擦，摩擦力矩随指数规律减小，最小时约为静摩擦力的60%，随后随着运动速度增大而增大。

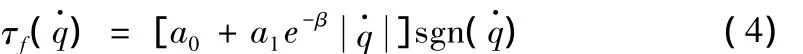
（2）Stribeck效应

主要表现为进入滑动摩擦后，在一定速度范围内产生“油膜”，从而导致摩擦力迅速降低。该效应描述了摩擦力与转速之间的稳态对应关系。

（3）动态滞后效应

指在静摩擦阶段，滑动速度和滑动摩擦力相应的延时。该效应是摩擦力的非常重要的特性之一，它的存在使得摩擦力建模更加复杂。

（4）可变最大静摩擦力

指静摩擦力大小会随着接触面间相对静止的时间变化而变化，运动以前相对静止时间越长，静摩擦力就越大［13］。

在伺服系统中，两个有相对运动或相对运动趋势的接触面上会产生摩擦力，而需要区别的是，因为在运动过程中，滑块与导轨接触面表面区域会发生轻微变形，导致滑块的速度与位移同滑块与接触面间的相对速度和相对位移的不同的［14］，从而在静摩擦状态下，相对运动速度为零而滑块的实际位移可能不为零。通常，钢质材料在静摩擦区域内的预位移为2～5 μm［15］。

1.3 摩擦力建模

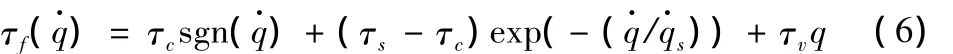
摩擦力模型采用包含库伦摩擦和粘性摩擦的指数模型:

实验证明，该模型的精度可达90%［16］。从式（6）中可以看出，模型与称非线性关系，故在实际使用时多采用线性化模型:

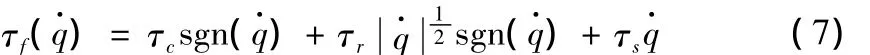
式中τc、τr、τv是随角速度变化的常数，分别描述了摩擦力矩的非平衡型、滑动粘滞现象和速度相关特性。

2 模糊神经网络

结构等价模糊神经网络的结构如图1所示。该网络共有四层，第0层为输入层，将输入信号转入下一层;第1层为求取隶属度层，是一个隐层型网络;第2层实现模糊集运算的功能，及得到神经元输出 μj，第1层和第2层的权系数为1;第三层确定每条规则的激活强度，并完成训练数据的后向传播，第2层和第3层的权系数是bj，需经过学习后确定;第4层是输出层，用重心法实现反模糊化功能，输出y。

神经网络的学习过程分3个阶段:

（1）前件参数和后件参数的初步确定

前件参数包括输入隶属函数的均值和方差，后件参数包括输出隶属函数的均值和方差。设输入论域为（－N，N），模糊分档数为奇数，则第i个隶属度的均值和方差ai，bi分别为:

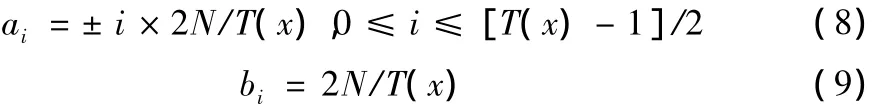
（2）控制规则的学习

把训练数据分别从输入输出端馈入网络，知道第2层的输出端和第3层的输出端，用微分竞争学习（DCL）提取有效的控制规则。算法为:

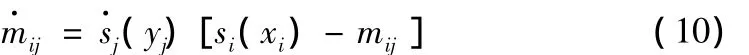
式中mij为第2层第i个神经元和第3层第j个神经元之间的连接权系数;sj（yj）为第3层第j个神经元的输出;si（xi）为第2层第i个神经元的输出。

学习结束后，保留权系数较大的连接，表示这条规则对控制起作用，取消较小的连接，表示该规则对控制输出不起作用。

（3）前件参数和后件参数的优化

控制规则确定后，根据训练数据进一步调整输入输出隶属函数的均值和方差，减小系统误差。本文采用BP算法，可表示为:

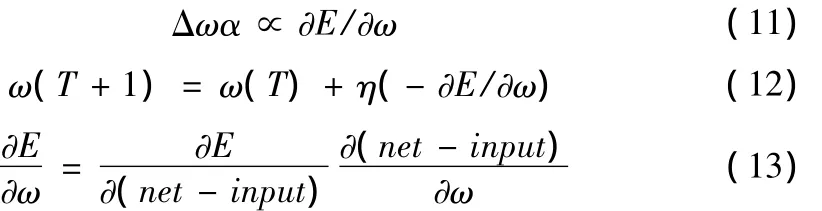
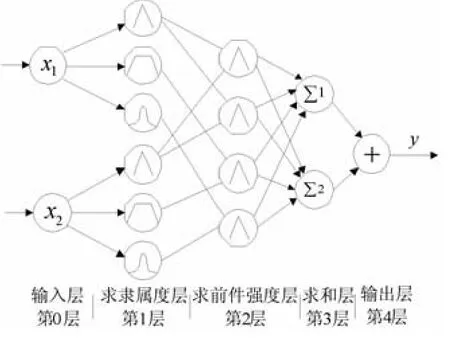
图1 结构等价模糊神经网络结构图

式中η为学习速率，按照上式可计算出输入输出隶属函数中均值和方差的修正量，不断调整参数知道输出满意的结果［17］。

3 控制系统设计

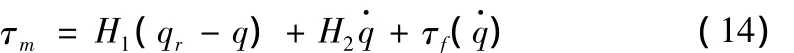
式中，q为角位移，τm为电机的输出力矩，τf为折算到电机轴上的等效摩擦力矩。H1=kp+ki/s，H2=kv，代入（6），可得:

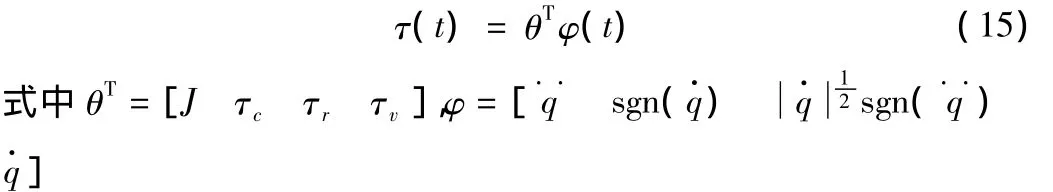
控制器模型为:

在实际的系统中，可令θ^为θ的估计值，e为误差，则有:模型辨识算法为:

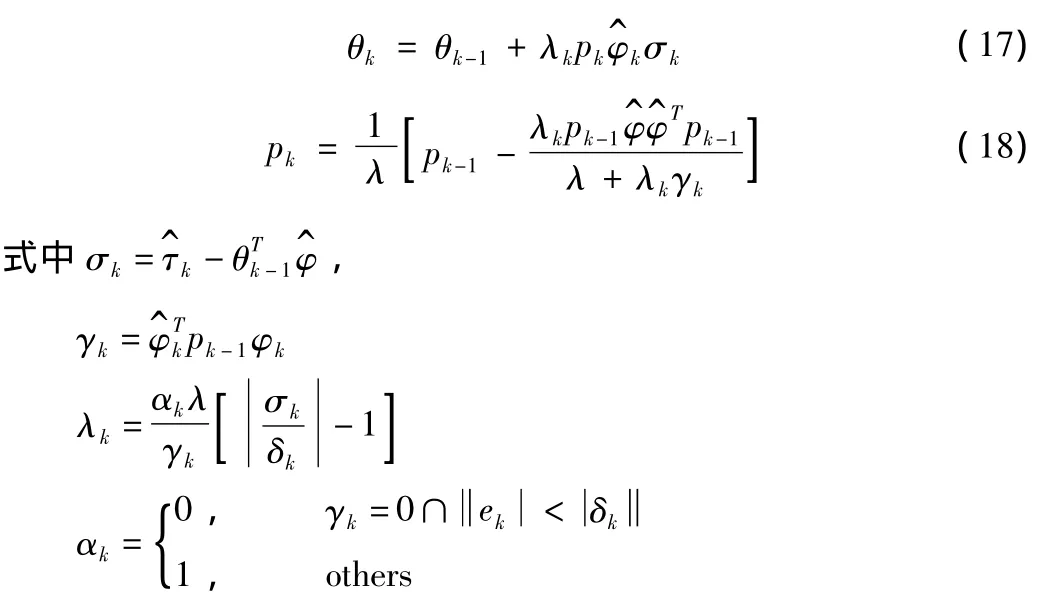
θ和θk即为在估计误差有节的假设下参数的最小二乘估计［9］。

基于模糊神经网络的摩擦力自适应补偿伺服系统结构图如图2，图中，ed为期待误差，执行机构为直流伺服电机，模糊神经网络控制器（FNN）通过采集到的数据进行学习，在线调整输出，控制器的输出u为FNN输出 ur与PID控制器输出uc之和，即u=ur+uc，FNN初试权值为零，在初试阶段PID控制器的输出占主导地位，FNN通过训练逐渐使u'r逼近u，从而是误差e趋于零，最终取代PID控制器的作用。在出现干扰时，由于PID控制的快速性可以保证其重新起作用以确保控制系统的稳定性和鲁棒性，同时由于FNN的作用可以提高系统的准确性和自适应能力［18］。

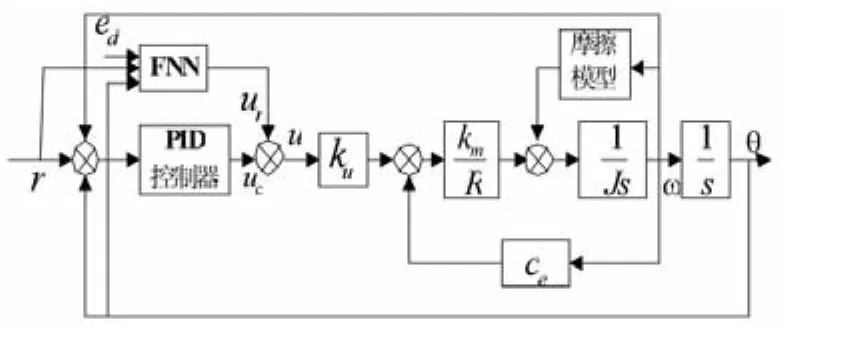
图2 自适应补偿系统结构图

在使用时设一误差容限δ，当 |u（k）－u'r（k）|≤δ时，权值不变，当| u（k）－u'r（k）| ＞δ时，则需对权值进行修正，修正公式为:

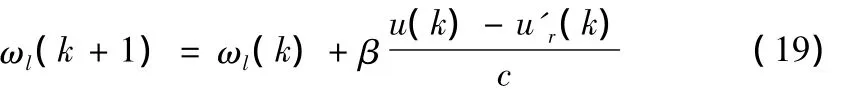
4 实验结果分析

作者在一条形绝缘材料摩擦力传动伺服实验台上，进行了数据采集工作，用采集到的数据对FNN进行训练，分别选用正弦跟踪信号和方波信号进行了实验，PID控制器参数为kp=0.52，ki=0.1，kd=0.000 ，β=0.013，c=48。采集到的摩擦驱动轮角速度ωr与条形材料传动速率v的关系如图3所示。

图4所示为无补偿和FNN补偿后的启动曲线，从图上可以看出，在启动过程中无补偿系统与补偿后系统相比有明显的振荡，调节时间较长，在稳态时也因干扰引起较大误差，而补偿后的调节时间明显减小，对因速度引起的摩擦力变化等非线性因素有着姣好的抵抗能力，稳态误差非常小。

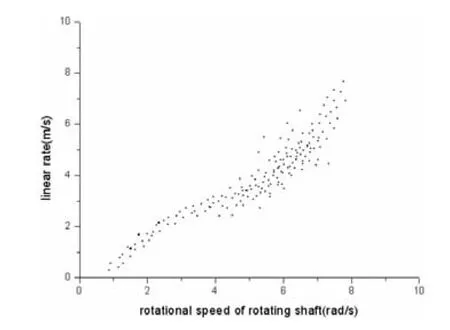
图3 驱动轮角速度与材料传动速率采样图

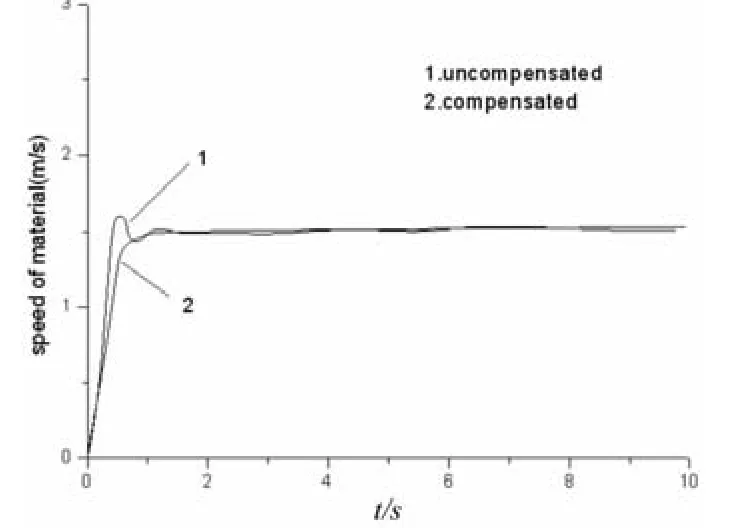
图4 启动过程曲线

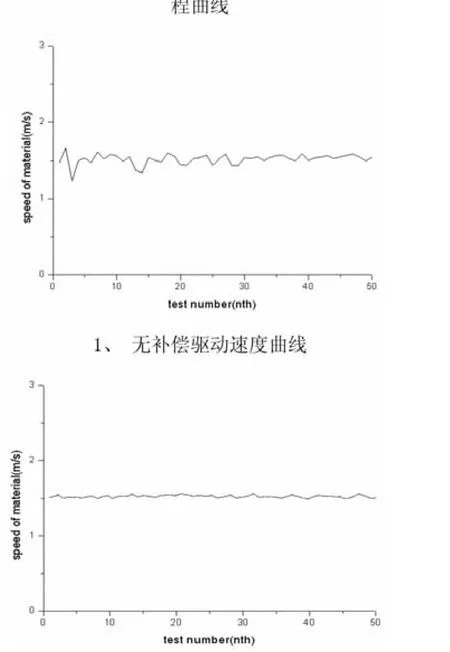
图5 使用不同条形材料驱动速度曲线

图5所示为多次使用不同光滑程度的条形材料分别进行未经补偿及FNN在线补偿后的测试结果，驱动速度均为稳态速度。测试结果表明，未加补偿时，稳态误差较大，最大达到32.47%，加入模糊神经网络补偿器后，对摩擦力的非线性因素及各种干扰，控制系统具有更高的跟踪精度，能够很好的抵抗摩擦和外部干扰，并具有较好的鲁棒性，当惯性系统发生改变时，FNN可以通过其自学习能力很好的补偿各种非线性因素带来的不确定性，具有很好的稳态精度。

5 结束语

本文通过对变压器专用条形绝缘材料自动冲床的条形材料摩擦驱动系统的非线性特性进行分析，基于模糊神经网络进行摩擦力补偿，提出了一种模糊神经网络PID摩擦力驱动控制模型，通过多次试验对FNN网络进行训练。实验结果表明，使用模糊神经PID控制，克服了因摩擦力的非线性特性引起的较大稳态误差及逼近误差，可以获得相对于常规PID控制更高的动、静态特性。由于神经网络控制器可以使用现有控制器实现硬件化，能够适用于不确定光滑程度被加工对象的控制，因此具有较高的工程实用价值。

［1］郑言海，杨志民，庄显义.大型目标模拟器方位伺服电机的对偶自校正 PID控制［J］.中国电机工程学报，2000，20（6）:84－88.

［2］张东纯，曾鸣，苏宝库.基于重复控制的动态补偿器及其在恒速调节系统中的应用［J］.中国电机工程学报，2001，21（7）:95 －97.

［3］克晶，苏宝库，曾鸣.考虑模型不确定性的基于分解控制直流电机系统的摩擦补偿方法［J］.中国电机工程学报，2003，23（10）:119－124.

［4］王明彦，郭奔.基于迭代学习控制的电动私服负载模拟器［J］.中国电机工程学报，2003，23（12）:123 －126.

［5］方一鸣，王乐，王益群.具有电枢反应非线性不确定性的直流电机速度鲁棒跟踪控制研究［J］.中国电机工程学报，2003，23（5）:136－139.

［6］AUBIN W C，BROGLISTO B.Adaptive friction compensation in robot manipulations:low velocities［J］.Int.J.Rovotics System，1991，10（3）:189－199.

［7］ ASTROM W C，BRAUM K.Adaptive friction compansation in DC－motor drives［J］.IEEE J.Robot and Automation，1987，3（6）:589 －681.

［8］徐丽娜.神经网络控制［M］.2版.北京:电子工业出版社，2003:1－2.

［9］张媚，李秀娟.伺服系统的神经网络摩擦力自适应补偿研究［J］.计算机仿真，2003，20（12）:70 －73.

［10］ HESS D P，SOON A.Friction at a lubricated LINC contract operating at oscillating sliding velocities［J］.J.Tribol.，1990，112（10）:147－152.

［11］ ARMSTRONG H B.Control of machines with friction［M］.Boston MA:Kluwer，1991.

［12］ JOHANNES V I，GREEN M A，BROCKLEY C A.The role of the rate of application of the tangential forcc in determining the static friction coefficient［J］.Wear，1973，24（1）:381 －385.

［13］刘强，尔联洁，刘金琨.摩擦非线性环节的特性、建模与控制补偿综述［J］.系统工程与电子技术，2002，24（11）:45 －52.

［14］陈学东，姜伟，李斌.高速直线运动系统非线性摩擦力建模研究［J］.中国机械工程，2006，17（18）:1934 －1938.

［15］ CANUDAS W C，OLSSON H，ASTROM K J，et al.A new model for control of systems with friction［J］.IEEE Trans.Automat Contr.，1995，40（3）:419－425.

［16］ ARMSTRONG B.Friction:Experimental determination，modelling and compensation［C］//IEEE Int.Cong.On Robotics and Automation，Philade，1988:1422－1427.

［17］曾光奇，胡均安，王东，等.模糊控制理论与工程应用［M］.2版.武汉:华中科技大学出版社，2009:183－186.

［18］叶军.伺服系统在摩擦条件下的模拟复合正交神经网络控制［J］.中国电机工程学报，2005，25（17）:127－130.