基于单神经元PID的异步电动机转速的自适应控制
2013-09-20杨友林巫庆辉
杨友林, 巫庆辉
(渤海大学工学院,辽宁 锦州 121013)
0 引言
异步电动机结构简单、维护方便、运行可靠,具有取代直流电动机的趋势。但它的转速与其旋转磁场的同步转速有转差率,因而调速性能较差[1]。为了解决异步电动机的调速问题,模拟直流电动机的矢量控制已成为异步电动机控制的一种标准方法。根据异步电动机的动态数学模型具有多变量、非线性、强耦合、慢时变等特征,基于转子磁链定向的矢量控制和基于定子磁链定向的直接转矩控制在实际中被广泛的应用[2]。在上述控制方法构建的调速系统中,转速调节器是其中重要的组成部分。一般调速系统中通常采用的是PI控制器,虽然结构简单,性能稳定,但在运行过程中产生参数调整困难,自适应性差,调速稳态精度低等问题[3]。本文依据调速系统中转速调节器的性能要求,设计单神经元PID控制器,将其应用于基于转差频率控制的调速系统中,利用神经元的自学习能力提高转速控制的自适应性。仿真实验表明基于单神经元PID的转速调节器提高了电动机调速系统的稳态精度,表现出较好的动态性能。
1 异步电动机的转差频率控制
对于异步电动机的控制,常用的方法是通过矢量变换将异步电动机和直流电动机建立等效关系,使异步电动机可以按照直流电动机的控制模式进行控制[4]。按转子磁链定向,在两相旋转坐标系dq上,异步电动机的转矩控制方程为:


由式(1)和式(2)可以看出,在保持转子磁链不变的情况下,电动机的转矩直接由定子电流的转矩分量isq控制。而转子磁链可以通过定子电流的励磁分量isd计算。假设ω1为定子角频率,ωs为转差角频率,则:
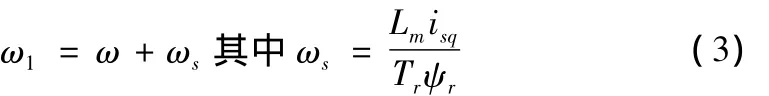
转子磁链:

若ψr恒定,转矩与转差角频率成正比。所以,可以用转差角频率控制代替转矩控制。转差频率控制系统结构如图1所示。
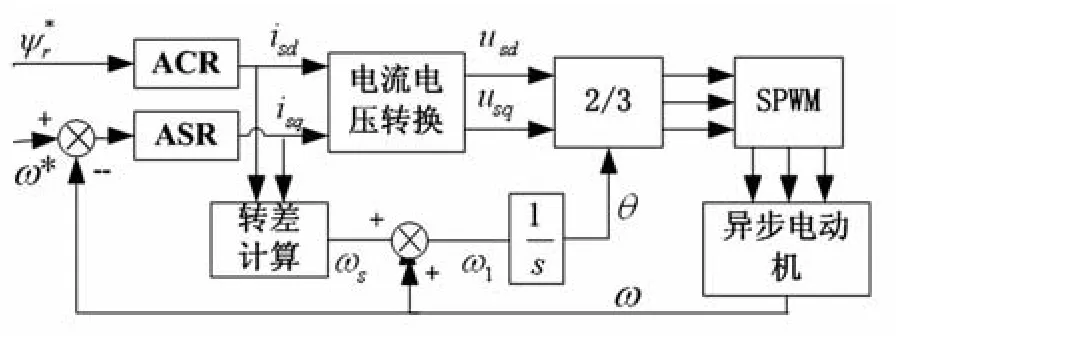
图1 转差频率控制系统结构
由式(1)和式(3)得:
在系统中以转速调节器ASR的输出为定子电流的转矩分量isq,通过电流调节器ACR控制定子电流的励磁分量isd,保持转子磁链恒定。此时,dψ/dt=0,由式(2)可得:

将电流控制转换为电压控制,方程为:
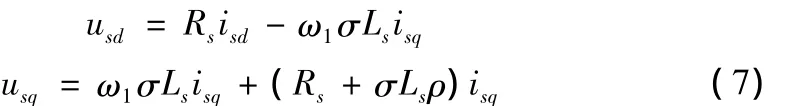
通过坐标变换,采用电源型逆变器,得到异步电动机三相电压信号。

联立式(3)和式(5)可得:
2 基于单神经元PID的转速调节器
在恒定磁链条件下,图1中电流调节器ACR采用弱磁控制模式[5]。本文重点研究的是转速调节器ASR,它的输出为定子电流的转矩分量isq。ASR的性能影响转速控制的效果[6],因此本文采用单神经元PID控制器,结构如图2所示。
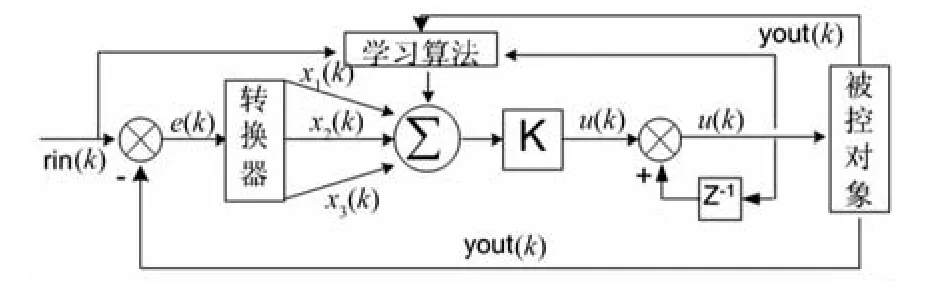
图2 单神经元PID控制器
图中rin(k)为设定值,被控对象的实际输出为yout(k)。
偏差e(k)=rin(k)-yout(k)作为转换器的输入,经转换器变换为单神经元学习所需的状态量:
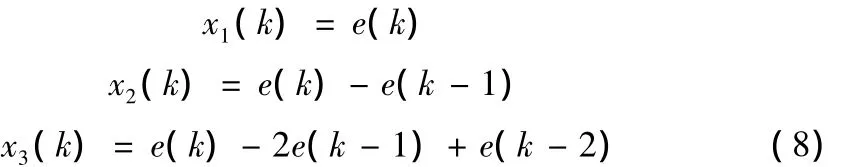
神经元通过对偏差的学习不断调整权值,权值对应于PID控制中的三个参数,从而产生控制信号u(k)=u(k-1)+Δu(k)。

wi(k)为对应于 xi(k)的权值(i=1,2,3,K(K >0)为神经元的比例系数。
神经元控制器通过学习算法实现权值的调整,权值与神经元的输入、输出和偏差均有关系[7],所以学习算法采用有监督的Hebb学习规则。
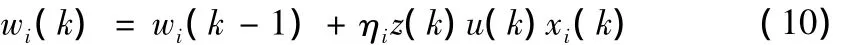
为了保证式(9)和学习算法式(10)的收敛性,需对上述算式进行规范化处理[8],则自适应控制器的控制律为:
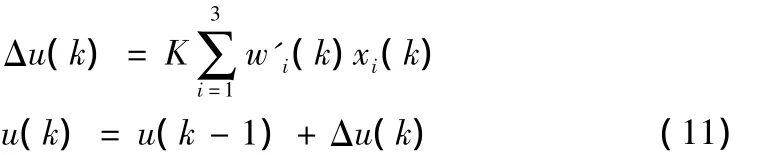
权值wi’(k)规范化为:
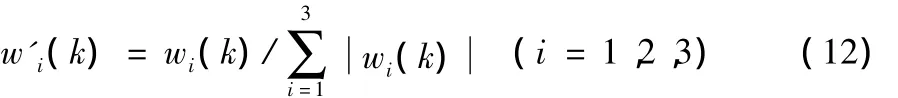
式中ηi为对应权值wi(k)的学习速率,z(k)=e(k)。
对于图2中的转速调节器ASR,输入为电动机实际转速与设定转速之差e(k)=ω*-ω,输出为定子电流的转矩分量u(k)=i,上述控制律提高了ASR在电动机运行时的自适应能力。
3 仿真实验及分析
采用图1所示的控制系统对三相笼式异步电动机进行MATLAB仿真研究。转速控制器ASR分别为PI控制器和单神经元自适应控制器,分析电动机在不同控制器作用下的起动和恒速加载的运行情况。电动机仿真参数设置如下:定子电阻Rs=0.435 Ω,转子电阻 Rr=0.816 Ω,定子电感 Ls=0.071 mH,转子电感 Lr=0.071 mH,互感 Lm=0.069 mH,极对数 np=2,转动惯量 J=0.19 kg·m2。
仿真实验中,首先电动机空载情况下起动,在起动后0.5 s突加负载TL=35 N·m,两种控制器下转速动态过程曲线局部如图3所示。
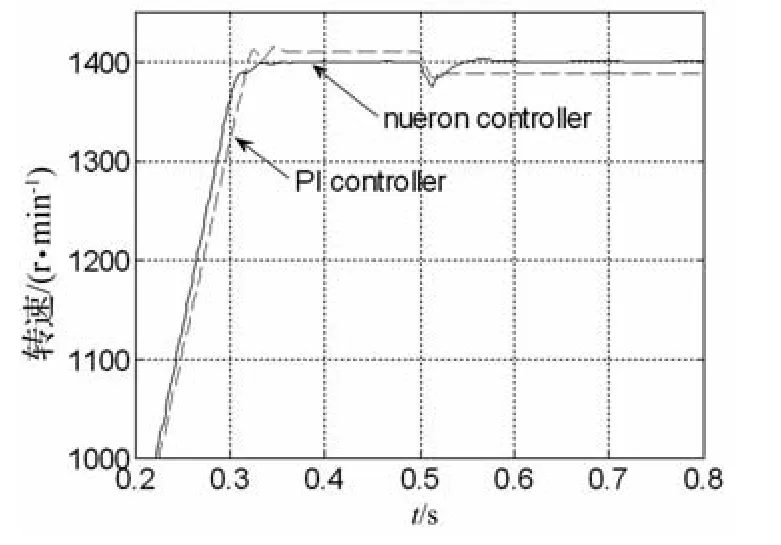
图3 恒速变负载转速响应曲线
图3中PI控制器的转速曲线在突加负载后明显偏离设定值,变化较大。而单神经元自适应控制器的转速曲线超调量小,恢复时间短,很快达到设定值。
电动机在恒定负载TL=35 N·m运行中,转速由1 400 r/min调至1 000 r/min,单神经元自适应控制器的转速动态曲线如图4所示。
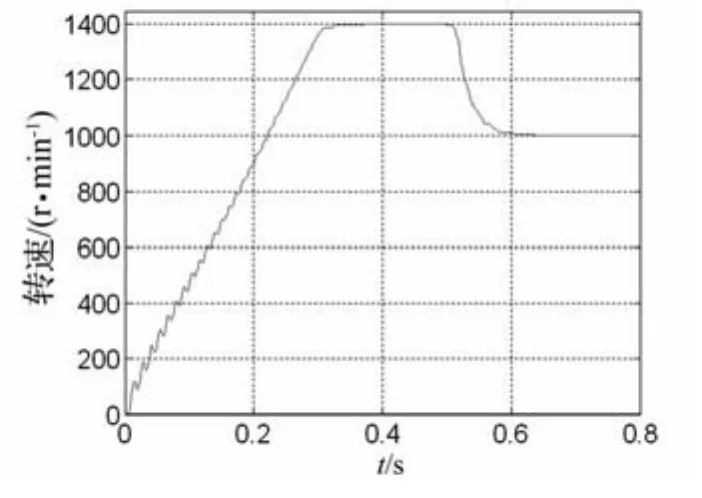
图4 恒负载变速转速响应曲线
由图4中曲线变化情况可以看出,转速变换平稳,无抖动;调速后稳态精度高,调节时间短。
4 结束语
仿真结果表明,基于单神经元的转速调节器在电动机恒速变负载和恒负载变速的实验中,表现出很强的自适应性,极大改善了异步电动机转速的控制效果。而且该控制器也可应用于其它矢量控制系统,作为系统的一部分,实现转速的自适应控制。
[1]陈伯时.电力拖动自动控制系统[M]3版.北京:机械工业出版社,2003.
[2]巫庆辉,伦淑娴.基于定转子电阻误差补偿的感应电动机自适应逆解耦控制研究[J].自动化学报,2010,36(2):297 -298.
[3]张敏.交流调速系统的单神经元自适应内模控制[J].电机与控制学报,2009,13(2):228 -230.
[4]付华,冯爱伟.基于单神经元控制器的异步电动机矢量控制[J].中国电机工程学报,2006,26(1):128 -130.[J].系统仿真学报,2005,17(9):2102 -2103.
[6]刘小斌,李梦达.异步电机单神经元自适应智能控制系统[J].化工自动化及仪表,2010,37(9):25 -26.
[7]王秀君,胡协和.一种改进的单神经元PID控制策略[J].浙江大学(工学版).2011,45(8):1499 -1500.
[8]杨友林.基于神经网络的PID参数自整定控制及其MATLAB仿真研究[J].甘肃联合大学学报(自然科学版).2011,25(4):62-63.
