巴特沃斯低通滤波器的实现方法研究

赵晓群，张 洁

(同济大学电子与信息工程学院，上海201804)

巴特沃斯(Butterworth)滤波器是一种具有最大平坦幅度响应的低通滤波器，它在通信领域里已有广泛应用。与贝塞尔(bessl)、契比雪夫(chebyshev)滤波器相比，巴特沃斯滤波器在线性相位、衰减斜率和加载特性3个方面具有特性均衡的优点，因此在实际使用中，巴特沃斯滤波器已被列为首选［1］。

Matlab语言是一种面向科学与工程计算的语言，它的测试程序手段丰富，扩展能力强，内涵丰富。信号处理工具箱(Signal Processing Toolbox)提供了设计巴特沃斯滤波器的函数，本文利用这些函数，进行了巴特沃斯滤波器的程序设计，并将其作为函数文件保存，可方便地进行调用。虽然Matlab拥有强大的数值运算功能，但编程运算效率并不高，对运行内存要求巨大，通过本文可以证明，在相同条件下，Matlab对程序的处理时间比C增加了200倍。因此在工程应用中，常常将C与Matlab结合起来运用。

1 巴特沃斯低通滤波器的特性

巴特沃斯低通滤波器的幅频特性模平方为

其中，N为滤波器的阶数，Ωc为低通滤波器的截止频率，当 Ω =Ωc时是滤波器的电压-3dB点或称半功率点。不同阶次N的巴特沃斯滤波器特性如图1，这一幅频特性具有如下特点:

(1)最大平坦性:可以证明在Ω=0点，它的前2N-1阶导数都等于零，这表示巴特沃斯滤波器在Ω=0附近一段范围内是非常平直的，它以原点的最大平坦性来逼近理想低通滤波器，“最平响应”即由此而得名。

(2)通带、阻带下降的单调性:这种滤波器具有良好的相频特性。

(3)3dB的不变性:随着N的增加，频带边缘下降越陡峭，越接近理想特性。但不管N是多少，幅频特性都通过-3dB点。当Ω=Ωc时，特性以20N dB/dec 速度下降［2］。

图1 巴特沃斯滤波器幅频特性

2 基于FFT的巴特沃斯低通滤波器设计方法

在连续时间系统中，可以利用卷积的方法求系统的零状态响应，这时，首先把激励信号分解为冲击函数序列，然后令每一冲激函数单独作用于系统求其冲激响应，最后把这些响应叠加即可得到系统对此激励信号的零状态响应。这个叠加的过程表现为求卷积积分。在离散时间系统中，可以采用大体相同的方法分析，由于离散信号本身就是一个不连续的序列，因此，激励信号分解为脉冲序列的工作就很容易完成，对应每个样值的激励，系统得到对此样值的响应，每一响应也是一个离散时间序列，把这些序列叠加即得到零状态响应。

若长度为N1的序列x(n)与长度为N2的序列h(n)做线卷积得到y(n)为有线长序列，其长度为N1+N2-1。共需要进行N1N2次乘法运算，在N1=N2=N的情况下，需N2次乘法运算。

如果把求线性卷积改为求圆周卷积，并借助FFT技术，有可能减少卷积所需的运算工作量。如图2给出直接卷积与快速卷积两种方案原理图。由图2(b)可见，快速卷积的过程中，共需要两次FFT，一次IFFT计算，相当于三次FFT的运算量。巴特沃斯低通滤波器的H(k)是知道的，数据已置于存储器中，实际只需要两个FFT运算量，如果假定N1=N2=N，经补零后点数为N1+N2-1≈2N，因而需要2×(Nlog22N)次复数乘法运算。此外，为完成X(k)与H(k)两序列相乘，还需要做2N次复乘。复乘运算全部次数为

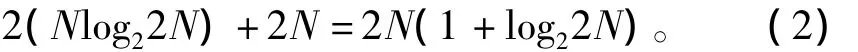
显然，随着N值增大，式(2)的数字要比N2显著减少。

图2 直接卷积与快速卷积原理方框图

当x(n)长度很长时，即N1≫N2，通常不允许等x(n)全部采集齐后再进行卷积，否则使输出相对于输入有较长的延时，另外，若N1+N2-1太大，h(n)要补上太多的零点，很不经济，且FFT的计算时间也要很长。为此，采用分段卷积的方法，即把x(n)分成长度与h(n)相仿的一段段，分别求出每段卷积的结果，然后用相应的方式把它们结合起来，便是总的输出。但是，N1可能很长，以至于趋于无穷大，以语音信号为例，如果不采用分段卷积的方法将迟迟不能给出结果，也无法找到那样大的储备来满足N1的需要［2］。但是即使采用分段卷积，也要根据语音的分帧，一帧帧输入语音，再对语音信号卷积，当前帧未输入完，不能进行卷积，因此也是有着相当大的时延，对于实时性要求较高的语音通信系统，这种方法没有本文给出的C语言实现的方法适用。

3 巴特沃斯低通滤波器的MATLAB实现

Matlab的信号处理工具箱提供了有关巴特沃斯滤波器的函数 buttap，buttord，butter［3］。

设计巴特沃斯滤波器的程序实现如下，Butter函数可在给定滤波器性能的情况下，选择巴特沃斯滤波器的阶数n和截止频率ωc，从而可利用butter函数设计巴特沃斯滤波器的传递函数［n，ωc］=buttord(ωp，ωs，Rp，Rs，'s')可得到满足性能的模拟巴特沃斯滤波器的最小阶数n及截止频率ωc，其中ωp为通带的拐角频率，ωs为阻带的拐角频率，ωp和ωs的单位均为rad/s;Rs为通带区的最大波动系数，Rp为Rs阻带区的最小衰减系数，Rp和 Rs的单位都为 dB。［b，a］=butter(n，ωc，'s')可设计截止频率为ωc的n阶低通模拟巴特沃斯滤波器.利用buttord函数、butter函数编制设计巴特沃斯低通滤波器的MATLAB函数文件butterdesign.m，其清单如下:

Function ［N，Wc，b，a］=butterdesign(Wp，Rp，Ws，As)

［N，Wc］=buttord(Wp，Ws，Rp，As，’s’);

［b，a］=butter(N，Wc，’s’);

［h，W］=freqs(b，a);

subplot(2，1，1);plot(W，abs(h));

subplot(2，1，2);plot(W，angle(h));

在低速率语音编码中，基音周期的判别准确性将直接影响解码端合成语音的质量，MELP编码器的基音提取中，首先要用截止频率为1 kHz的6阶巴特沃斯低通滤波器对语音信号进行滤s(n)波，消除语音帧中高频成分对基音周期估算的影响［4］。在这里我们用Matlab实现用截止频率为1 kHz的6阶巴特沃斯低通滤波器对语音信号s(n)来滤波。采样的一组语音信号:e=［5.405 1，64.149 0，80.667 6，115.356 8，48.432 1，-35.842 0，-90.292 7，-74.395 0，-97.388 3，-72.897 4 ］。调用函数［b，a］=butterπ(N，ωc)，N 为滤波器阶数 6，ωc是归一化截止频率0.25。得到系数b=［0.001 1，0.006 3，0.015 8，0.021 0，0.015 8，0.0063，0.001 1］，a=［1.000 0，-2.978 5，4.136 1，-3.259 8，1.517 3，-0.391 1，0.043 4］。根据系数就可以调用滤波器函数对信号实行滤波，y=filter(b，a，e)，得到结果y=［0.005 7，0.118 5，0.904 3，3.977 9，11.971 4，26.804 9，46.517 8，63.225 6，65.475 1，45.087 3］。y为滤波后的信号。

4 巴特沃斯滤波器的C语言实现

利用重复计算由差分方程得出的递推公式来实现线性时不变离散时间系统，根据线性时不变系统的直接I型和直接II型或规范型结构，系统的输入和输出满足如下差分方程［5］:

并具有如下系统函数:

M=N=6，将之前得到的系数a和b对应带入差分方程，在C语言下变成得到函数文件如下:

从结果可以看出，本文给出的基于C语言的设计方法与Matlab设计方法运行结果一致。

5 运行时空开销的比较

可以用tic，toc函数计算下在Matlab里面运行的时间为0.000 303 s。用clock函数对C函数计算得到的运行时间为0.000 000 333 s。

将同样数据的10个信号扩展到30个，Matlab运行时间0.000 394 s，C函数为0.000 001 33 s。将同样的10个信号扩展到60个，Matlab运行时间为0.000 516 s，C 函数为0.000 002 33 s。

将同样的信号扩展到150个，Matlab运行时间为0.001 090 s，C函数运行时间为0.000 005 33 s。

C语言运行时间效率要比用Matlab高得多，对于数字语音信号这样的运算，一般信号数字运算量是相当巨大的，当数字信号运算量越大，C语言进行计算的效率优势就越明显。

6 查看变量使用空间

在Matlab中命令窗口，用whos和whos global来查看所有局部和全局变量占用的内存大小［3］，可以看到a和b是7为双精度数值各56字节，e和y为输入和输出，是全部存在里面的，10个输入的话就有80字节，输出也是一样的。

在C函数中，除了输入输出共设立了4个数组，p数组只是为了显示用的，真正运行函数是不一定要用到的，a数组有6位占用48字节，b，x，y有7位双精度值有56字节，但是C函数有最大的优势，就是它的输入输出占用的空间是可以变化的，这与Matlab必须先存在程序中不同，对于大量数值信号的计算来说，这样是很费空间的，所以当计算数值数量越大时，C函数优势越明显。

7 结论

本文给出了一种用C语言实现巴特沃斯低通滤波器的方法，并且通过与Matlab巴特沃斯滤波器一般方法以及另一种快速圆周卷积设计方法的比较中，得出本文用的C语言实现的方法在时间开销以及运行时延等方面都比Matlab的方法要好，基于C语言的设计方法的处理时间是基于Matlab的设计方法的1/200。说明本文给出的算法在对于高实时性并且具有大输入信号量的通信系统中是具有很大优势的。不足之处由于大输入信号量的通信系统对于信号输入量要求很大，也只能分段传输处理，所以还是有一定的延时。

本课题由水声通信与海洋信息技术教育部重点实验室(厦门大学)资助。

［1］李钟慎.基于MATLAB设计巴特沃斯低通滤波器［J］.信息技术，2003，27(3):49-50.

［2］郑君里，应启行，杨为理.信号与系统［M］.北京:高等教育出版社，2000.

［3］张雪英.数字语音处理及MATLAB仿真［M］.北京:电子工业出版社，2010.

［4］韩笑蕾.(甚)低速率水声语音编码算法研究［D］.上海:同济大学，2012:57-58.

［5］OPPENHEIM A V，SCHAFER R W，BUCK J R.Discrete-Time signal processing［D］.Cambridge:Massachusetts Institute of Technology，1999:284-285.