浅谈级数的敛散性
2013-09-19王晓红
王晓红
(榆次第一职业中专学校,山西 晋中 0 3 0 6 0 0)
一、级数的相关概念
级数包括常数项级数和函数级数。研究级数时,我们要把常数项级数与函数级数全面考虑在内,这样才能整体性地掌握级数。
(一)常数项级数
1.常数项级数的定义
一般人们对事物数量特征方面的认识需要经过一段由近似到精确的过程。在这个认识事物数量特征的过程中,会遇到由有限个实数相加发展到无限个实数相加的问题。如:有一根绳子,每天取一半,那么可得
上式是一个无穷等比级数的和,且可以直观地得出其和是整数。
定义1:给定一个数列{U n},对它的各项依次用“+”号连接起来的表达式称为数项级数或无穷级数(也常简称级数),其中U n称为数项级数(1)的通项。
,称
它为数项级数(1)的第n个部分和,也简称部分和。
2.常见的常数项级数
是P—级数。
3.定义数项级数的敛散性
无穷数项级数和一般形式我们定义为Sn=U1+U2+
那么,无穷数项级数相加的“和数”有什么实质性的意义呢?由级数的定义(1)我们能够得一个数列{Sn},这里的{Sn},表示为则显然可得。下面给出常数项级数敛散性的定义:
定义2若数项级数(1)的部分和数列{Sn}收敛于S(即)
,则称数项级数(1)收敛,称 S为数项级数(1)的和,记作或。
若{Sn}是发散数列,则称数项级数(1)发散。
这里我们应该注意的是:讨论无穷级数的收敛问题时,实质上是研究部分和数列的收敛问题。
(二)函数项级数
1.函数项级数的定义
作为分析学分支之一的级数理论,与微积分学两者常常结合起来,出现在其他的分支中,两者都是将连续与离散结合起来以极限为基础来研究分析学的对象,即主要研究函数—变量之间的相互关系。级数作为研究函数的重要工具,无论是在理论方面还是在实际应用方面都有着重要的地位。
函数列是指定义在同一数集上的函数:f1,f2,f3,…,fn…,一般记为{fn}或 fn,n=1,2,3…下面给出函数项级数的定义。
定义3:设{un(x)}是定义在数集E上的一个函数列,表达式称为定义在E上的函数项级数,简记为。

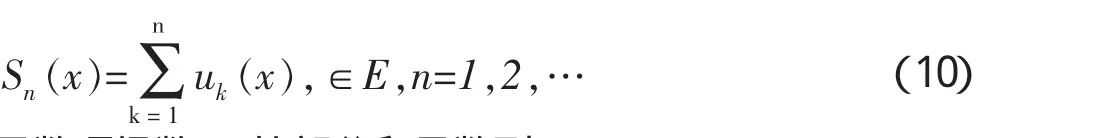
称为函数项级数(9)的部分和函数列。
2.函数项级数的敛散性
一个函数列{fn}若它在点X0收敛,怎么要求数列:f1(X)0,f(2X)0,f(3X)0,…f(nX)0,(X0E)收敛?若函数列收敛于数集 D,则有函数列 f1,f2,f3,…fn,…在数集 DE上的每一个点都收敛。函数项级数是由函数列的和组成的,函数项级数的敛散性见下:。
(3)P— 级数。
定义4:设{Sn(x)}是函数项级数Σun(x)的部分和函数列。若{Sn(x)}在数集D上一致收敛于函数Sn(x),则称函数项级数Σun(x)在D上一致收敛于函数S(x),或称Σun(x)在D上一致收敛。
二、级数敛散性的一些基本性质
级数的敛散性问题常常被看作是研究级数的首要问题。要研究级数的敛散性问题,下面先给出级数的一些基本性质:
,此处的α,β是任意的两个实数。
性质2:在级数中任意添加、删除、改变有限个项,不改变级数的敛散性。(可能影响级数的和)
性质3:对收敛的级数,可以任意添加括号而不会改变级数的收敛性与和。(可用于判定级数发散)
三、介绍级数敛散性的判别方法
级数的一些基本性质可以帮助我们判断级数的敛散性,但是在实际问题中,仅仅利用级数的基本性质判断级数的敛散性是远远不够的,往往有一定的困难性。因此,除了运用级数的基本性质判断级数的敛散性外,还有一些重要的级数敛散性判别法能够简洁方便地判断一类级数的敛散性。论文将着重介绍这些判别方法,如柯西判别法、阿贝耳判别法、狄利克雷判别法、达朗贝尔判别法。
(一)Cauchy判别法
无论是正项级数判别敛散性,还是函数级数判别敛散性都用到了柯西判别法。可见,柯西判别法在级数敛散性的判别中有着重要的作用。
1.柯西判别法在正项级数中的应用
在正项级数中的柯西判别法也称作是根式判别法。一般的根式判别法指的是:设正项级数为Σan,an的n次根存在,且an的n次根的极限等于正常数q,即存在
。则有:
(2)如果级数发散,则从某一项起q>1。
(3)如果级数的敛散性不定,则q=1。
,可得an≤qn,当0<q<1时,等比
级数Σqn收敛,根据比较原则,级数在0<q<1
时也收敛。
时发散。
的敛
散性。
证:因

则
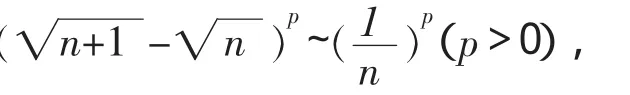
即

所以
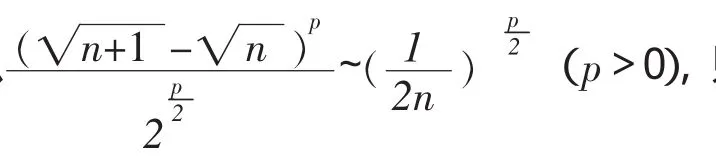
2.柯西判别法在函数项级数中的应用
柯西判别法在函数项级数中应用广泛,是函数项级数判断敛散性的一种基本方法。
收敛→←对任给的ε>0,存在 N,使得当 n>N时,对一切自然数 p成立。
,可得 bn=n,则级数
发散。又因为。


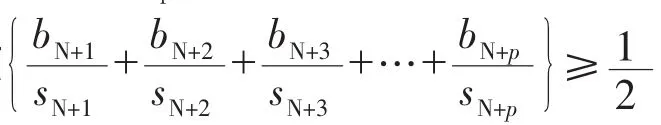
在 p,使,根据Cauchy
(二)Adel判别法
1.阿贝耳判别法在数项级数中的应用
Adel(阿贝耳)判别法:设
(1){an}是单调有界数列;
,且an
综上可得:{an}是单调有界数列,级数是收敛的,根据阿贝耳判别法得级数是收敛的。
2.判别法在函数项级数中的应用
(x∈I)若有:
(1){an}在 I上一致有界,且对每个固定的 x∈I,{an}是非负递减数列。
在I一致收敛.则级数在I上收敛。
则可得a的取值范围为
n
2时,an取最小值,当h=2时,an取最大值。
由上可得,an有界收敛,由阿贝
(三)Dirichlet判别法
狄利克雷判别法主要用于判定数项级数的敛散性、函数项级数的一致收敛等等。通常狄利克雷判别法与阿贝耳判别法合在一起称之为A-D判别法。
1.狄利克雷判别法在数项级数中的应用
Dirichle(t狄利克雷)判别法:若数列bn单调且n→∞时bn→0,而级数
Σanbn的部分和数列sn有界,则级数收敛。
在区间[m,n]上的敛散性。
。
界的。
在区间[m,n]
上是一致收敛的。
2.狄利克雷判别法在函数项级数中的应用
Dirichle(t狄利克雷)判别法:设:
(1)部分和A(nx)在M上一致有界。
(2)当n→∞时,在M上b(nx)0。
(3)对于任何固定的 x∈M,数列{bn(x)}都是单调的。那么,级数在M上一致收敛。
根据狄利克雷判别法,b=1单调趋于0,有界,那么nn级数收敛。
在解题过程中,能用阿贝耳判别法的也一定能用狄利克雷判别法,但是,能用狄利克雷判别法不一定能用阿贝耳判别法,这是因为阿贝耳判别法的判别条件要比狄利克雷判别法的判别条件严谨一些。
(四)D’Alembert判别法
在级数敛散性的判别中,通常达朗贝尔判别法也称之为比式判别法。
不为0,且满足lim
。
在应用达朗贝尔判别法选几何级数做标准的时候,
1,但级数是发散
是收敛的。由达朗贝尔判别法知判断级
四、典型的例子
单调趋于0。
收敛。
由上可得,在判别一些级数的敛散性问题时,有时可以应用多种判别法进行证明,但是并不是所有的判别法一定都适用,所以我们应该选择合适的判别法来判别级数的敛散性。
判断级数的敛散性的方法很多,但在做题过程中只有选用合适的判定方法进行判断,才能巧妙、快速地解答,在提高解题效率的同时,还可以保证正确率,以能够达到事半功倍的效果。
[1]邢家省.华东师范大学数学系[M].北京:高等教育出版社,2001.
[2]孙玉泉,王永革.数学分析学习巩固与提高(上册)[M].北京:机械工业出版社,2011.
[3]宋国柱.分析中的基本定理和典型方法[M].北京:科学出版社,2004.
[4]周民强.数学分析(第二册)[M].上海:上海科学技术出版社,2003:.
[5](俄罗斯)阿黑波夫.数学分析讲义[M].王昆杨,译.北京:高等教育出版社,2006.
[6]尹小玲,邓东皋.数学分析简明教程(第二版下册)[M].北京:高等教育出版社,2006.
