关注“断层” 有效衔接——小学生运算技能弱化的归因分析和对策
2013-09-19赵芳燕
赵芳燕
(奉化市西坞街道白杜小学,浙江 奉化 315500)
运算是一切数学活动的基础,也是小学数学的一条教学主线。良好的运算能力既是学生今后学习数学的奠基,也是一个人必备的基本数学素养之一。课程改革对运算教学提出了很多新的理念,但在实践中却又出现了新的问题,笔者在一项问卷调查中发现,教师普遍对新课程实施以来学生的计算技能发展持不乐观态度,集中反映的问题有:计算正确率呈下降趋势,运算能力不稳定;基础运算掌握较好,但综合运算的速度大幅下降;班级中部分学生不能够灵活运算,对运算产生厌倦感等等。
不可否认,运算教学的终极目标不仅仅是让学生具有比较熟练的运算技能,但这绝不是要放弃对运算技能的关注。运算是技能和思考的结合,运算能力含结果和过程两个方面。结果应该是正确的,过程应该是简洁合理的。在实践课改优秀理念的同时,如何最大限度地避免运算技能的弱化现象,达到过程与结果的和谐统一?这就需要我们更深入地分析学生运算能力的形成过程。从教育心理学角度来看,运算能力的形成一般要经过认知、分解、组合、自动化四个阶段。认知阶段主要是让学生理解算理、明确方法,随着学习的深入,复杂的运算技能又总是可以分解为若干单一的技能,对分解的单一技能进行必要的训练并逐渐组合,才能形成复合型技能,再通过综合性训练达到自动化阶段。审视这四个关键阶段,我们的教学又缺失了什么?带着这样的视角去观察,我们不难找到其中存在着的几个“断层”。
断层一:运算形式与内涵思考
模仿学习在小学阶段仍占有较高比重,运算方法或过程常常也是以规范的形式展现出来的,然而很多学生往往是知其然而不知其所以然,其认知水平上的运算方法与知识结构水平上的算理脱节,也就特别会出错。比如在多位数乘法中,面对每次乘得的积的对位问题,有的学生只是记住了“阶梯状”的对位形式,可是一旦遇到了因数中间或末尾有0的情况,错误率就会大大增加,因为学生的认知停留在形式模仿上而缺少对算理的理解。
断层二:新授技能与分解技能
如果我们将小学阶段的运算体系看作是一幢大厦,那么基础的加、减、乘、除一步运算无疑是这幢大厦的基石。之后学习的运算无论有多么复杂,都可以分解为若干个基础技能。如除数是一位数的除法,其实就是“除、乘、减”一步运算的反复,三位数乘两位数,就可以分解为多次的乘加运算。但在实际教学中,教师往往忽视了对复杂运算的分解,将其看作是全新的知识来教学,这就会导致在算法探究上无法突出主次;再者,对学生缺乏必要的多样化分解指导,往往为运算而运算,为单一方法而方法,不知灵活变通,久而久之,学生思维趋于僵化,减缓了运算技能的形成。
断层三:低级运算与高级运算
如果我们把学生在一二年级学习的加减乘除一步运算称之为低级运算,那么之后在此基础上学习的运算则可称之为高级运算。从低一级运算到高一级运算的过渡看似循序渐进,但如何更好地将技能组合衔接却至关重要。高一级运算往往需要学生有娴熟的“基本功”。如在多位数乘一位数的运算中,学生的学习难点不是运算法则或书写格式,而是进位问题,如58乘9,学生在算到“五九四十五”再加前面进上来的7时最容易出错,什么原因?因为学生在竖式中,进行的运算是“不可视”的乘加口算,而在平时的口算练习中,可视性的乘加口算也很少,更不用说不可视口算了,因此学生错误较多。
断层四:技能习得与自动化
运算作为小学阶段学生学习的一块重要内容,在每一册中都有几个单元的分布,这些单元互相联系、互为基础,共同螺旋构成了学生的运算学习体系,也是学生运算技能发展的主要路径。两个相关联的运算单元间往往隔着其他知识的学习,这期间的衔接容易出现断层;再加上实验教材中基本运算题量减幅较大,运算训练的断续影响了学生运算技能的自动化水平。
综上所述,导致学生运算技能弱化的“断层”在运算技能形成的各个阶段均有分布。换句话说,如果在技能形成的认知和分解阶段,教师能够带领学生有效经历“算法探究——算理体悟——分解形成”的全过程,那么无疑为后续训练奠定了坚实的基础;如果在技能形成的组合和自动化阶段,教师能够“胸有全局”“瞻前顾后”,降低运算阶梯间的跨度、合理孕伏针对性和长效性训练,那么学生运算技能的熟练度、正确性和灵活性就能得到有效保证。基于这样的思考,笔者以为在当前的运算教学中,我们需要及时修复各个阶段的“断层”,做好关键点的衔接工作,从而最大限度地修正学生运算技能的弱化现象。
一、加深算理体悟,有效衔接算法形式与内涵思考
众所周知,“算理”是学生走向“算法”的桥梁,过于注重“算法”的形式化模仿,固然可以在短期内收到一定效果,却犹如空中楼阁,很难稳固。过多的形式化模仿还会使学生在运算学习中偏重结果的简单化获取,偏废对运算过程的内涵思考。因此,教师应注重在每一次的算法探究阶段精心设计算理体悟环节,从而为算法的形成提供有力支撑、为后续学习打下坚实基础。
如在教学“笔算除数是一位数除法”一课时,一位教师为了让学生更好地理解“两层竖式”的算理,掌握算法,设计了如下环节:
(1)根据情境操作:48个桃子,平均分给两只猴子,怎么分呢?用小棒代替桃子分一分,并用数学的方式把分的过程表示出来。
(2)反馈方法,并辅以课件演示:
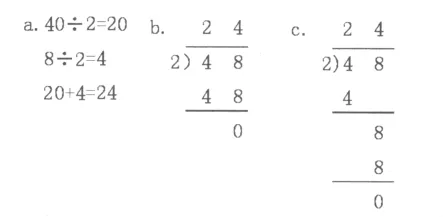
(3)讨论:这些方法都能清楚地表示出分桃子的过程吗?(得出,分层竖式能更清楚)
(4)建立联系:分层竖式与第一种横式在方法上有什么相同的地方?(使用色块使竖式计算与横式进行对照)
(5)再次演示分小棒的过程,学生边说算理边写竖式。
在上述环节中,教师采用“直观操作——方法表征——讨论深化——联系比较——梳理内化”的流程,使学生在“数形结合”的具体背景下建构起分层竖式的计算模型,在这个过程中,学生既有对分层竖式的优势感悟,又有对每一层竖式、每一个数的内涵理解,使得学生的运算不再是简单的形式模仿。
再如《乘法分配律》,很多老师往往比较强调对于(a+b)×c=a×c+b×c的形式,然而若遇到 64×36+64×64或者64×99+64的题时,就有很大一部分学生无所适从,无法灵活运用简算。究其原因就在于学生缺乏对算法内涵的思考,如果在运算定律探究中能够紧密结合具体情境或线段图,引导学生通过情境联系、数形结合的方式整体着眼,想清楚是“几个64”加(减)“几个64”,并且加强此类训练,那么学生对于乘法分配律的结构理解就能更深刻清晰。
当然,要想切实加深学生对算理的感悟,我们还要根据学生的年龄特点和教学内容选择合适的策略。如学习退位减法时直观的动手操作、学习分数乘法时的数形结合、学习运算定律时的举例归纳等等,在算理理解的同时要关注学生思维的同步和外化(语言表述),从而在手、口、脑等感官的协作参与下立体地感悟算理,为技能的形成奠基。
二、注重灵活分解,有效衔接新旧运算技能
运算教学的关键一点就是要根据学生的学习建构特点,引导学生把新知分解成若干个基本技能,降低学习难度,纳入自己的已有技能体系之中。
以《多位数乘一位数》为例,我们首先要明确的是:不要把这节课作为全新的知识去教学,因为从运算过程来看,它其实可以分解成多次乘加。换言之,只要学生有了这种“分解”的意识,那么算法的形成也就不存在多大的困难。为此,我们可以在学生理解算理、初步形成算法后引导学生思考:“在计算多位数乘一位数时,我们用到了哪些过去的知识?”“如果第一个因数有5位、6位甚至更多,我们怎样去运算?”从而让学生认识到多位数乘一位数时,不管其中一个因数有几位,都可以分解成几次简单的乘加,从而将其更快地纳入到旧有的技能体系中。
当然,上例只能作为运算分解的第一层次,我们姑且称之为通法,即按标准程序运算。其实,学生的技算技能强弱归根到底还与自身的数感有着密切的联系。拥有良好数感的学生在运算时往往能够摆脱固有模式,善于从不同的角度思考问题,重建思维模式,且对数的大小、结果正确与否有着敏锐的直觉。因此,在教学中,教师更要充分关注学生对数的灵活分解,倡导算法多样化,增强学生的“数感”。如“252×4”的运算中,除按标准程序笔算外,学生还可以有如下个性化算法:
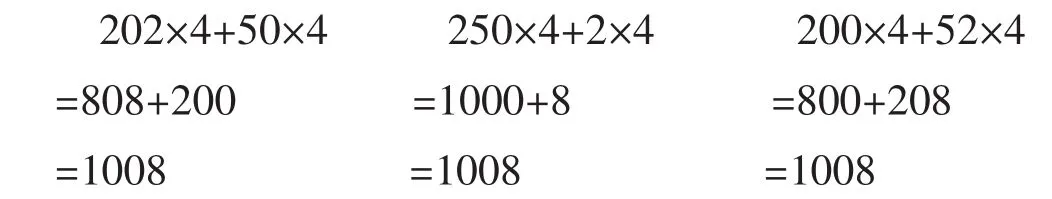
允许和鼓励学生通过对数的具体拆分,将新知灵活地分解为较简单的几步,使新旧技能进行充分的融合,使学生在一次次的分解中积累相关经验,提高运算技能。要做到这一点,就需要教师吃透教材,厘清各种运算间的联系,在教学中不仅关注对算理的感悟和理解,更要时时渗透“转化”意识、“灵活运算”意识,由繁及简,通过对新知的灵活分解更快地消化新知。
三、重视基本功训练,有效衔接低高级运算
“基本功”是指学习某一个知识点、解决某一个问题策略所需要的基础,对这些基本功,宜采取“早期孕伏、提前训练”的方法,有意识地渗透在前期有关内容的学习中。小学各阶段学生运算学习呈螺旋上升状态,从口算到笔算到混合运算,从一步运算到两、三步运算,每一次的技能提升都必须以之前技能为基础,许多学生往往是没有具备一定的基本功,构成了高一级运算技能形成的“绊脚石”。
仍以乘除法笔算为例,学生之前已经学习了基本的加减乘除口算,正确率也较高,但为什么一到笔算,即便老师讲清了算理与算法,学生还是频频出错呢?显然并不是因为他们不会做,而是在笔算乘除法之间需要两项“基本功”:笔算乘法中的进位需要在头脑中进行乘加两步运算;笔算除法则需要在头脑中完成试商、调商的过程。抓住了这两点,也就为学生口算和笔算的顺利过渡铺好了台阶。有些老师虽然考虑到了这点,在口算练习中也有乘加、( )里最大能填几等练习,但训练不够到位,不妨在练习乘加口算时,增加“不可视”的口算,比如听算练习;在练习( )里最大能填几时,尤其加强诸如48×( )<150之类的方法指导和练习,这样一来就为打通不同运算类型、不同运算难度之间的壁垒做好了充足准备,有利于提高运算的正确率和速度。
正所谓“磨刀不误砍柴功”。一般来说,在不同形式和类型的运算学习前,都需要教师分析学生需要的基础和掌握情况,提前进行针对性的基本功训练。如学习“异分母分数加减法”之前对通分的训练、“小数除法”之前对小数点移动的训练等等。在训练时,要特别关注前置性、有效性和针对性,而不是临时抱佛脚。
四、合理规划训练,有效衔接技能习得与自动化
课标修订稿指出:“教师应把握技能形成的阶段性,根据内容的要求和学生的实际,分层次落实。”运算技能的形成和巩固需要有足够的练习次数和时间,同时注重训练的实效性。对学生运算技能的训练既需要一定的集中训练,也需要细水长流式的分散性、过渡性训练,从当前现状来看,教师往往能够较好地关注前者,而对后者则缺乏关注。
基于此,我们在教学中不妨采取“集中训练”与“分散训练”交错进行的方法。比如在“小数除法”学习初期,安排学生每天进行6~8题的集中训练,接下来每周做3~4次运算练习,每次2~4道,分散到其他单元学习中作为补充,并依次拉长练习的距离。在分散训练期间,既要突出重点,加强对小数除法的运算训练,也要统筹兼顾,穿插小数乘法、整数四则运算、简便运算等内容;还要做到“动态调整”,即根据学生运算中的易错类型设计训练内容。这样细水长流式的练习负担不重,持之以恒必将提高运算的正确率和速度,加快学生从运算技能的“习得”向“自动化”转变的进程。
总之,学生运算技能的形成依赖于每个阶段的有效落实,我们不能将学生运算技能的弱化简单地归结于个体差异、教材编排等因素,而要着眼于学生运算技能的发展变化过程,细致修复其间可能出现的“断层”,有效做好衔接工作,才能更好地帮助学生形成良好的运算技能。
[1]唐少雄.注重探究过程形成运算技能http://bcy.shuren100.com/wwrs/170435.shtml.2008(12).
[2]江义英.对运算技能训练的思考[OL]http://www.doc88.com/p-29755424166.html.2010(18).
[3]张天孝 .小学新思维数学研究[M].浙江大学出版社2011(07).
