把握追问时机 点亮智慧课堂
2013-06-02杨素文
杨素文
(台州黄岩院桥初级中学,浙江 台州 318025)
法国教育家保罗·弗荣雷说过:“没有对话,就没有交流,也就没有真正的教育,课堂应该是对话的课堂。”在数学课堂上实施教学,激发学生进行积极的思维活动,数学教师就要不断地向学生提出问题,为学生营造课堂“问题空间”,引起学生主动思考。但是,教师很多时候所提出的问题,学生只需回答“是”、“不是”,“对”还是“不对”或者简单说出答案。要使学生对问题更深入地思考,教师需要进一步地追问学生。就教学来说,教师的追问就是围绕教学目标,设置一系列问题,将系列问题与课堂临时生成的问题进行整合,巧妙穿插,由浅入深,由此及彼地提问,以形成严密而有节奏的课堂教学流程。追问不仅是课堂预设的生成和重新建构,也是课堂效能的关键所在。教师的有效追问,能够有效开发学生的最近发展区,提升学生的认知潜力,激发学生积极思维能力,可以使课堂锦上添花,课堂教学效果最优化,促进学生的全面发展。因此,教师要驾驭好“追问”,让“追问”更有效地为课堂教学服务。
一、追问于错误时——去伪存真
布鲁纳曾经说过:“学生的错误都是有价值的。”的确如此,错误是孩子最朴实的思想、最真实的经验。学习过程是一个尝试错误的“过程”,通过尝试错误,一方面可充分暴露学生思维过程的薄弱环节有利于教师的“对症下药”;另一方面,错误是正确的先导,有时错误比正确更具有价值,所以数学课堂教学中,学生的错误往往是一种鲜活的教学资源,教师应该善于挖掘和发现学生错误背后隐藏的教育价值,引领学生从错中求知,从错中探究。在学生出现判断错误时,如果教师给与学生一定暗示性的追问,就能有效帮助学生纠正错误,巩固和强化数学知识。
案例1:《圆的切线》的教学。
判断题:已知⊙O的半径为5cm,直线L上一点P到圆心的距离等于5cm,则直线L与⊙O相切。出示了题目后,很多学生认为此题正确,都说:“这符合切线的一个判定方法,与圆心的距离等于半径的直线是圆的切线。”老师追问:“直线与圆心的距离等于半径是什么意思?”通过追问,让学生区分点与点之间的距离与点到线之间的距离是不相同的,一个学生马上举手回答说:“这里的距离是指点到直线的距离。”老师又追问:“直线L上一点P到圆心O的距离等于半径是不是就是直线与圆心的距离等于半径?”此时学生的认知矛盾已深刻化解,这时老师又追问:“你能画出符合题意的反例示意图吗?”意在让学生能更深一步找到自己错误的原因,从而扫除思维障碍。
案例中,教师以自身特有的敏锐和机智捕捉到学生学习过程中的“差错”,并发现这“差错”背后隐藏的教育价值,教师并非立即否定学生而是抓住学生的错误体验,利用学生的认知冲突,选择合适的追问策略,让学生明白产生错误的原因,从而得出正确结论。
二、追问于难点时——画龙点睛
教学效果的好坏取决于教师对数学教学核心——数学问题的思考价值的把握程度,数学教学要突出重点,突破难点,努力突显数学思想,追问是突破数学难度的催化剂,教师要善于抓住教学的难点,选取突破口进行追问,在追问中引领学生透过现象进行深入的比较和辨析,把一些非本质的属性撇开,把一些本质的属性抽象出来加以概括,从而突破教学的难点。
案例2:《合并同类项》的教学。
填空题:若-2a4mb和27a8b3-n能合并成一项,那么值是多少?面对问题,大部分学生思维受阻,思考了一会儿,不知从何下手,此时老师依次进行如下的追问:“你们知道两个单项式在什么情况下能合并?”学生回答道:“当两个单项式是同类项时能合并”,老师追问道:“你知道什么是同类项吗?”学生回答到:“所含字母相同,相同字母的指数也相同”,老师又追问道:“请你对照定义的文字解释一下定义中的3个相同”,学生稍作思考便答道:“只要满足4m=8,1=3-2n就能求出m和n的值了。”
案例中,教师通过对教学重点,难点的把握,及时进行连续追问,并没有因为大部分学生思维的受阻,就让会做的学生讲解或自己讲,而是通过连续追问,把深藏的问题层层揭开,起到了画龙点睛的作用,让学生体会到解决问题成功的的喜悦,并进一步加强了学生对学习数学的兴趣。
三、追问于困惑时——提升领悟
“困惑”即学生由于多种想法交织在一起,没有很好的判断力进行取舍,觉得这种思路也对,那种方法也好,这时就需要老师给予更多的有效追问,将思维引向深入,找到解决问题的办法,从而解决问题困惑的地方。
案例3:《解一元一次方程》的教学。
例题:某同学将等式3a-2b=2a-2b变形,两边都加上2b得3a=2a,两边都除以a得3=2,你能指出他错在哪里吗?学生在解决此题时,都觉得解题过程似乎没有错,但结果肯定是错的,但不知道究竟错在哪里,感到非常困惑,教师追问到:“仔细思考一下,每一步的依据是什么?”学生回答道:“第一步依据是等式性质一,第二步是等式性质二,都没有错啊!”老师追问道:“在利用等式性质二解题时应注意什么条件?”这时学生才恍然大悟,老师又追问道:“以后将等式两边同时除以一个数或式时应注意什么?”学生马上回答到:“当除式不为0时,两边才可以同除以这个数或式,否则不能。”
古人也云:“学贵有疑”,只有让学生在质疑探索中真正明白自己所困惑的问题,才能使理解和记忆更加深刻,才能把要学习的知识和能力转化为个人的发展。
四、追问于无疑时——激活思维
数学是一门逻辑性很强的学科,数学知识之间存在着一定的联系,一个阶段的学习结束后,教师便会问:“同学们,还有什么疑问吗?”班上学生大都摇头示意“无”,教师往往很满足这种“无疑”的状态,事实上课堂上的生成是可以诱发的,教师要借助于教学文书,把握契机,在文本的空白处挖掘数学知识之间的联系,适时追问,引领学生发掘文本,促成拓展延伸,提升文本价值,让学生在课堂上再形成一次思维的高潮。
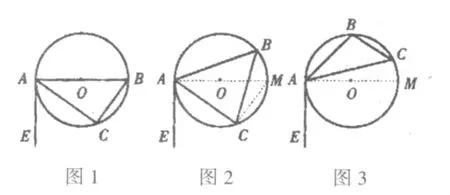
案例4:已知如图(1)△ABC内接于⊙O,AB为⊙O直径,∠CAE=∠B。求证:AE与⊙O相切。对于本题大部分同学都觉得非常简单,要证明AE与⊙O相切,只要证∠EAC+∠BAC=90°,而由AB是直径,∠-CAB+∠B=90°,∠CAE=∠B,所以∠CAB+∠EAC=90°,老师问道:“如图2:若锐角△ABC内接于⊙O,∠-CAE=∠B,求证:与⊙O相切”。学生思考了一会儿,仍找不到证明的思路,老师追问道:“要想证明AE是切线,点A在抛物线上,如何作辅助线?”学生回答道:“点在圆上,作半径,证垂直”,老师又追问道:“能否把这个问题转化到第1题中去”,很快学生作出辅助线,找到了解决问题的思路,老师继续追问道:“如图3,若钝角△ABC内接于⊙O,∠CAE=∠B,求证:AE与⊙O相切”。由于有了上题作为铺垫,学生就自然而然地想到添辅助线,把这个问题转化到第1题中去,顿时,课堂上学生踊跃发言,各抒己见,再一次形成思维的高潮。
案例中,在教师的多次追问下,学生通过“一题多变”掌握了一类问题的实质和思维规律,实现了较高层次的抽象和概括,克服了思维的保守性,培养了思维的灵活性,如果教师的解题教学始终停留在解完就结束问题的层面上,那么题海战术就永远不会消失,教师应充分利用学生获得的现有资源和思维成果及时进行总结、反思、拓展、延伸,使问题的价值获得最大化,通过适时追问,打开学生思维的“闸门”,激发学生乐于表达自我价值观的欲望,从而拓展延伸文本的空间,在本文空白处彰显追问的智慧,体现了课堂有效追问的魅力。
五、追问于意外时——生成精彩
叶澜老师曾经说过:“课堂就是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的风景,而不是一切都必须遵循固定的路线而没有激情的行程。”课堂上随时都会发生意外,然而一些教师仅仅把它看成教学过程中的“节外生枝”,所以一旦出现“意外”,或一句话搪塞“这个问题,我们以后再来研究”,或不予理睬,避而不谈,甚至加以批评,这些都是不利于学生思维的培养的,因此教师要敢于打破预设的框架,对学生意外的回答给予积极的回应和鼓励,并用睿智的追问,激发学生的思维,延伸思维空间,让教学中的“节外生枝”演绎出独特的价值。
案例5:《函数》复习教学。
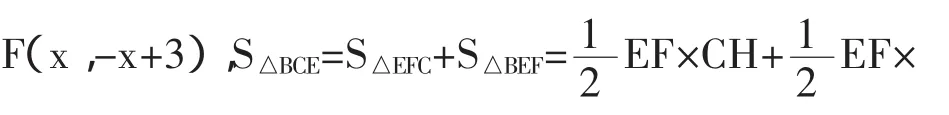
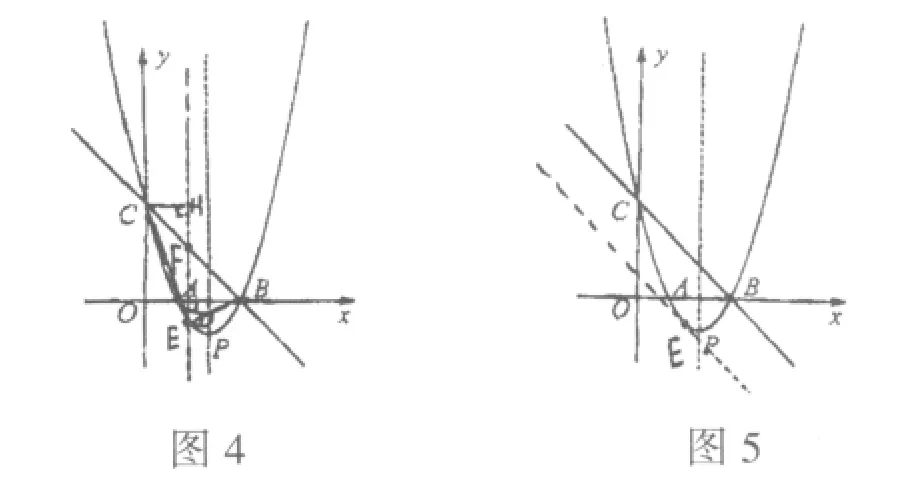
在案例中,如果教师没有及时而有效的追问,课堂中不曾预约的精彩是不会不期而至的,不言而喻,正是由于充分利用教学中的“节外生枝”,因势利导适时追问,才擦出了学生思维的火花,使学生丰富的数学思维得到淋漓尽致的发挥。
总之,追问不是漫无目的的询问,它应是以更好地完成教学目标为导向;追问不是毫无感情的质问,它应以促进学生发展、呵护学生自尊为前提;追问不是喋喋不休的盘问,它应集中反应教师的教学智慧,引导学生进行有意义的智力思维活动,追问既是一门学问,更是一门艺术,它是教师教学智慧和教学艺术的体现,是教师真情投入,深情流露、适时捕捉的结果,追问可以提高质量,开启智慧,提升品味,追问掀起课堂的高潮,演绎课堂的精彩。
[1]李忠衡.数学课堂中的追问艺术[J].教学与管理,2008(10).
[2]孙保华.如何在数学教学中进行有效追问[J].教学与管理,2010(1).
[3]王小琴“追问”搭台“思维”唱戏——例谈初中数学“以问促思”的教学策略[J].中学数学(初中版),2012(10).
[4]赵绪昌.追问在数学课堂教学中的运用[J].中学数学(初中版),2012(3).
