伴随卫星轨控时机与相对运动椭圆大小控制效率的关系

吴会英，陈宏宇，周美江，慕忠成

(上海微小卫星工程中心，上海，201203)

1 引言

随着航天技术的发展，伴随小卫星协助主航天器开展完成航天任务越来越受到人们的关注。伴随小卫星一般搭载主航天器进入轨道，一段时间后从主航天器释放，通过轨道机动形成伴随飞行轨道［1-4］。由于伴随卫星携带燃料较少，故而希望利用其既有资源以最大效率地进行轨道调整。在轨控量一定的情况下，控制时机和控制方向是轨控策略的核心。本文基于相对运动方程，在速度增量大小一定的前提下，对伴随卫星最大效率轨道调整的控制时机和控制方向进行推导，并用仿真实例来验证理论的正确性。最后以伴随卫星从主星释放后的轨道驻留为例，给出其燃料最省的轨控策略。

2 相对轨道控制理论

2.1 相对运动理论

伴随卫星从主星释放后协助主星开展航天任务，二者之间的距离相比其地心距很小(小于千分之一)，可用相对运动理论进行研究。根据文献［1］的推导结果，在主星轨道坐标系下，相对运动方程的解为:

主星轨道坐标系定义为:原点在主航天器质心，x轴径向朝天，y轴在轨道面内垂直于x轴沿飞行方向，z轴符合右手法则。n为主星轨道角速度。

由相对运动方程的解可知，相对运动可分解为轨道面内和垂直于轨道面两个独立的运动，本文只研究轨道面内的相对运动情况。现引入参数b和φ角，使:

则(1)式可写成如下参数形式:

其中，

参数解的几何意义是一轨道面内长半轴为短半轴两倍的沿迹方向漂移椭圆:

2.2 轨控时机对控制效率的影响

由上文推导可知，对伴随卫星的轨道控制会改变相对运动椭圆的大小。由于伴随卫星携带燃料有限，所以需要选择合适的控制时机和控制方向，最大效率地改变相对椭圆的大小。当控制量为相对小量时，对(2)式求全微分，将(4)式代入可得:

设控制量v与y轴正方向的夹角为θ，则有ΔVy=vcosθ，ΔVx=vsinθ，那么:

其中θ0为引入的参数角，其计算表达式如下:

2.2.1 Δb取最大值时的控制时机和控制角度1)控制角度约束

由相对运动参数方程(4)式可知相对运动曲线的倾斜角φ满足:

结合上面(10)式易知 tan θ=tan φ，θ=kπ +φ，即速度增量作用方向与相对运动方向平行;

小结:速度增量的作用方向与相对运动方向平行是最大效率地改变相对椭圆大小的必要条件。

2)控制时机约束

小结:在速度增量平行于相对运动方向的前提下，在相对椭圆径向上、下点控制，对相对椭圆大小的改变效率最高。

小结:在速度增量平行于相对运动方向的前提下，在相对椭圆径向中点进行控制，对相对椭圆大小的改变效率最小。

3)总结

平行于相对运动方向作用的速度增量对相对椭圆大小的改变效率最高。其中在相对椭圆上、下点作用的速度增量对相对椭圆大小的改变量最大，在相对椭圆径向中点作用的速度增量对相对椭圆大小的改变量最小。沿相对运动方向作用的速度增量将增大相对椭圆，反相对运动方向作用的速度增量会减小相对椭圆。

2.2.2 Δb为零时的控制时机和控制角度

Δb=0 时，sin(θ+θ0)=0，θ+ θ0=kπ，θ0=kπ-θ，有:

tanθ0=-2tan(nt+φ)⇒tanθ=2tan(nt+φ)

而相对运动曲线倾斜角tanφ=-1/2cot(nt+φ)，那么 tanφ ×tanθ=-1，即速度增量的作用方向与相对运动方向垂直。

小结:在相对运动椭圆的任意点作用与相对运动方向垂直的速度增量都不改变相对椭圆的大小。

2.2.3 结论

平行于相对运动方向作用的速度增量是最大效率改变相对椭圆大小的必要条件，其中在相对椭圆径向上、下点作用速度增量对相对椭圆大小的改变效率最高;垂直于相对运动方向作用速度增量不改变相对椭圆的大小。为便于理解，用图1～2来说明上述理论，其中绿色箭头为相对运动方向，蓝色箭头为控制方向。

图1 平行于相对运动方向控制Fig.1 Control direction is parallel to the relative movement

图2 垂直于相对运动方向Fig.2 Control direction is horizontal to the relative movement

3 仿真实例

3.1 形成伴随飞行椭圆

伴随卫星释放前搭载在主星上，轨道根数如表1所示。

表1 仿真初始轨道根数Table 1 Initial elements for simulation

初始时刻对伴随卫星施加反沿迹方向0.2 m/s的速度增量，伴随卫星从主星释放。半轨(46分20秒)后再次施加沿迹方向0.2 m/s的速度增量，形成如图3所示的伴随飞行椭圆。椭圆中心(1.7，0)，椭圆短半轴长0.708 km。仿真采用STK的HPOP模型［5］，忽略摄动影响。

图3 初始伴随飞行椭圆Fig.3 Initial company flight ellipse

选择图4所示的特征点进行仿真验算，其中红色箭头为相对运动方向，绿色箭头为控制方向。

图4 仿真控制点Fig.4 Controlling points of the simulation

3.2 特征点仿真

对控制点1～4施加图4所示的速度增量，速度增量作用前后伴随卫星在主星轨道坐标系下的运动曲线如图5～8所示。其中红色曲线表示原始绕飞椭圆，蓝色曲线表示进行轨道机动后的绕飞椭圆。

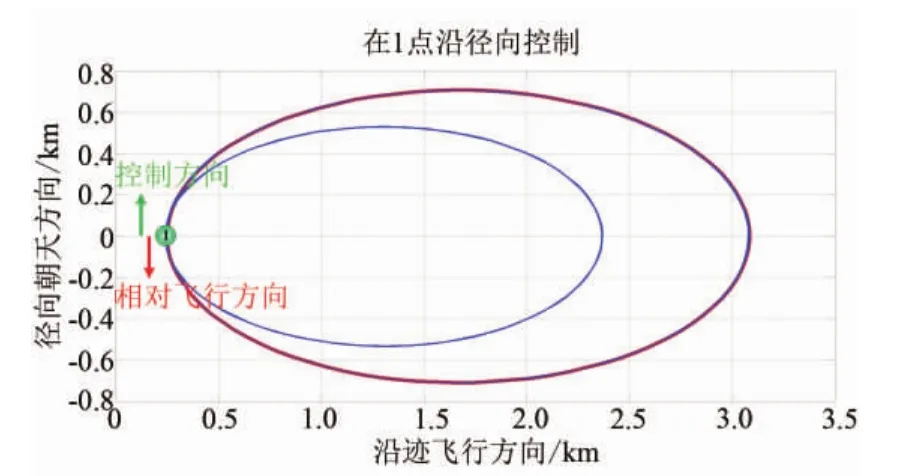
图5 在1点沿径向控制Fig.5 Curves for controlled at point 1

图6 在3点沿径向控制Fig.6 Curves for controlled at point 3

图7 在2点沿迹向控制Fig.7 Curves for controlled at point 2

表2 平行于相对飞行方向控制仿真结果与理论结果对比Table 2 Comparisons between theoretical results and simulating results for the parallel control

表3 垂直于相对飞行方向控制仿真结果与理论结果对比Table 3 Comparisons between theoretical results and simulating results for the horizontal control

图8 在4点沿迹向控制Fig.8 Curves for controlled at point 4

仿真结果如表2所示，其结果验证了理论的正确性。

仿真中发现在控制点5、6垂直于飞行方向施加速度增量，相对椭圆大小的改变量不为零，但推迟或提前一定时刻，则可使改变量为零。对控制点1、2、3、4作用垂直于飞行方向的速度增量的仿真也出现这一现象，如表3所示。

出现这种情况的原因是:前面的理论是基于控制量为相对小量导出的，而本文仿真实例中，初始相对椭圆短半轴b=708 m，控制量引起的相对椭圆短半轴改变量Δb为10～102m量级，Δb相对b不为小量，需精确推导Δb的表达式。

设初始相对椭圆短半轴为b，控制量ΔVy、ΔVs使相对椭圆短半轴改变量为Δb，则有:

式(12)中的两式相减，再代入式(4)，可得:

容易看出，当控制量引起的相对椭圆短半轴改变量Δb相对于初始相对椭圆短半轴b为小量时，(13)式忽略小量就是(7)式。

本文的仿真实例不能忽略小量，用(7)式近似表达Δb会导致理论计算与仿真结果有一定的偏差。但对特征点的仿真发现，垂直于相对运动方向控制体现出了这一偏差，而平行于相对运动方向控制理论计算与仿真结果一致，没有体现出这一偏差。下面以控制点2和控制点3为例，对平行于相对运动方向控制和垂直于相对运动方向控制两种情况，用(7)式近似表示Δb引起的偏差进行定量分析。

3.2.1 垂直于相对运动方向进行控制

1)控制点3:nt+φ =0°，ΔVy=0.2 m/s，ΔVx=0

由(13)式可知精确的相对椭圆短半轴改变量为，

与表3中仿真结果Δb=83.7 m一致。

2)控制点2:nt+φ =270°，ΔVy=0，ΔVx=0.2 m/s

由(13)式可知精确的相对椭圆短半轴改变量为:

与表3中仿真结果Δb=21.9m一致。

3)其他特征点垂直于相对运动方向控制精确的相对椭圆短半轴改变量计算方法同上。

计算表明当控制量引起的相对椭圆短半轴改变量Δb相对于初始相对椭圆短半轴不为小量时，垂直相对运动方向的控制并非不改变相对椭圆短半轴长度的控制方式，近似表达导致的偏差可用上面的方法计算出来。

3.2.2 平行于相对运动方向进行控制

1)控制点3:nt+φ =0°，ΔVy=0，ΔVx=0.2 m/s

由(13)式可知精确的相对椭圆短半轴改变量为:

从公式(7)可知近似的Δb表达为:

近似表达与精确表达一致。

2)控制点2:nt+φ =270°，ΔVy=0.2 m/s，ΔVx=0

由(13)式可知精确的相对椭圆短半轴改变量为:

从公式(7)可知近似的Δb表达为:

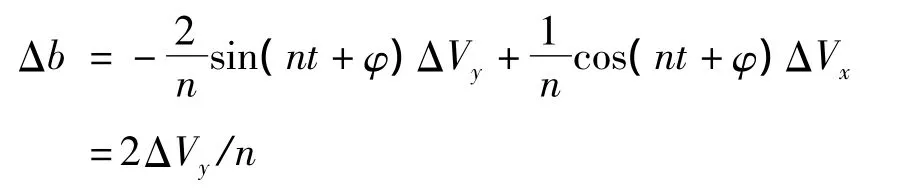
近似表达和精确表达一致。

3)其他特征点平行于相对运动方向控制Δb的近似表达与精确表达也一致。

计算表明，即使控制量引起的相对椭圆短半轴改变量Δb相对初始相对椭圆短半轴b不为小量，但用近似表达进行分析，仿真结果也和理论结果吻合得很好。

3.3 燃料最省的轨道驻留轨控策略

以主航天器伴随卫星的实际释放为例，应用上面理论求解伴星与主星在同一轨道上并超前主星2 km以上驻留的轨控策略。伴星相对主星的释放速度大小为0.5 m/s，释放方向如图9所示。

图9 伴星释放示意图Fig.9 Release sketch of company satellite

由相对运动理论可知，伴星释放后会形成相对主星的沿迹方向漂移椭圆，椭圆短半轴长由公式(2)计算可得b=462.20 m。

如果只做一次控制，需要在相对运动椭圆上与释放点相同相位的点处施加与释放速度增量大小相等、方向相反的控制，再考虑伴星超前主星2 km的条件，控制效果如图10所示。

图10 伴星释放后一次轨控示意图Fig.10 One-time orbit controlling curve after the company satellite released

根据本文的理论，可知图10的一次控制其控制时机非效率最高，现分解为两次控制:

1)第一次控制在相对运动椭圆径向上点作用沿迹方向、大小等于Δv1=y·0的速度增量，以形成伴随飞行椭圆，由(2)式可知此时相对椭圆短半轴减小:Δb1=153.72 m。

第一次控制效果如图11所示，红色曲线为从伴星释放到第一次轨控的漂移椭圆，蓝色曲线为第一次轨控后形成的伴随飞行椭圆。

图11 伴星释放后两次轨控第一次控制Fig.11 Curves of first control in two-time orbit control after the company satellite released

2)第二次控制在径向中点作用沿径向的速度增量，速度增量大小应恰好将当前的相对椭圆短半轴减小为零，以达到相对驻留，所以第二次控制的速度增量大小为:Δb2=0.34848 m/s。

第二次控制效果如图12所示，绿色五角星为第二次轨控点，第二次轨控后伴随卫星相对椭圆短半轴减小为零，相对主星在这个点驻留。

图12 伴随卫星释放后两次轨控第二次控制Fig.12 Curves of second control curves in two-time or bit control after the company satellite released

综上所述，若只进行一次轨控，所需速度增量Δv=0.5 m/s;若进行两次轨控，所需速度增量Δv=|Δv1|+|Δv2|=0.4553 m/s，小于一次控制所需速度增量，是燃料最省的轨控方案。

4 结论

本文通过理论推导和仿真结合的方法给出了伴随卫星控制时机对于改变相对运动椭圆大小的效率的影响，证明了:平行于相对运动方向进行轨控是最大效率改变相对运动椭圆大小的必要条件，其中在相对运动椭圆径向上、下点进行轨控的效率最高。以主航天器伴随卫星的轨道驻留为例，应用这个理论求解了燃料最省并满足约束的轨控方案。

［1］ 郗晓宁，王威，高玉东.近地航天器轨道基础［M］.长沙:国防科技大学出版社，2003:193，247-250.

［2］ 杨维廉.椭圆轨迹编队飞行轨道分析［J］.中国空间科学技术，2001，21(5):1-6.

［3］ 黄美丽，向开恒.编队飞行卫星相对轨道摄动运动分析［J］.中国空间科学技术，2006，3(6):13-19.

［4］ 张育林，曾国强，王兆魁，等.分布式卫星系统理论及应用［M］.北京:科学出版社，2008:25-31.

［5］ 丁溯泉，张波，刘世勇.STK在航天任务仿真分析中的应用［M］.北京:国防工业出版社，2011:17.