基于提升小波与RLS的涡轮泵故障检测方法
2013-09-19钟福利
钟福利,李 辉
(电子科技大学航空航天学院,成都611731)
1 引言
随着航天技术的快速发展,运载火箭的可靠性和安全性受到广泛的重视,其故障检测和诊断技术研究是一项十分重要的研究课题,得到许多研究人员和学者的关注[1-2]。涡轮泵是液体火箭发动机重要的机械部件之一,其结构十分复杂,物理环境极端,在发动机的部件中所占故障比率最高[3]。涡轮泵的故障扩展十分迅速,故障危害极大,故开展涡轮泵故障检测,对减少由于涡轮泵故障造成的损失具有重要意义。近年来,国内外对运载火箭发动机及其涡轮泵等的健康监控研究也取得了一系列成果[2,4-5],其中健康监测方法大部分以振动信号的时域特征、频域特征、时频域特征分析为基础[6]。
基于时域信号统计特征的涡轮泵故障检测算法较为普遍,有ATA算法、多特征参量自适应阈值综合决策算法、涡轮泵实时故障检测短数据均值自适应阈值算法[7-9]等。此类算法计算直接、简便,计算量较小,运算速度快,实时性较好,但时域统计特征受随机因素影响较大,使检测中出现虚警和漏警的概率相对较大。基于频域特征的故障检测算法[10-11],涉及的变换复杂,计算量较大,检测的速度较慢,而且此类算法以信号平稳为前提,这对非平稳信号则会失效。基于时频域的故障检测算法,较典型的有以小波变换为基础的检测算法[12],具有较好的分析非平稳信号和信号局部特性检测能力,但也存在运算量相对较大的问题。
在机械故障检测中,由于经典小波变换同时具有时域和频域局部化特性,且有快速算法,故其得到了广泛的应用。随着小波提升方案的提出,小波分析的研究领域得到大大拓展。提升小波方案直接在时域或空域构造小波,具有算法简单、计算速度快的特点[13]。递推最小二乘算法(RLS)中滤波器的参数可用迭代的方式自适应更新,收敛速度快,并且具有较好的跟踪系统和环境的动态变化的能力[14]。
因此,本文结合提升小波变换和RLS算法的优点,针对涡轮泵的稳态运行过程,提出一种基于提升小波与RLS的涡轮泵故障检测方法,为涡轮泵的健康监控提供一种故障检测方法。利用提升小波变换获取每个检测步长信号段的逼近信号和细节信号,计算每步各层细节信号和逼近信号的均方根以及峭度,计算逼近信号和细节信号的加权平均均方根、逼近信号的加权平均峭度和细节信号的加权平均峭度作为故障特征,分别提取逼近信号与细节信号的加权平均均方根和加权平均峭度作为故障特征,用RLS算法进行加权平均均方根特征序列滤波处理,根据给出的故障判别计算方法和故障判别方法分析涡轮泵的故障情况,并用某型发动机涡轮泵壳体振动加速度信号对方法进行了验证。
2 检测原理
2.1 提升小波变换
小波提升形式给出小波完全的空间域解释,具有结构简单,原位运算,节省存储空间,运算量低,逆变换可直接反转实现,有可逆的整数到整数的变换等优点。根据文献[13][15]和[16]对提升小波原理作如下简介。
将给定的信号分解成逼近信号和细节信号,提升小波的提升方案实现包括分裂、预测和更新3个步骤:
1)分裂 将输入信号Si分成Si-1和Di-1两个小波子集,分解过程用FdivSi=(Si-1,Di-1)表示。将输入信号按序号的奇偶分成两组Ei-1(偶数号序列S2j)和Oi-1(奇数号序列S2j+1)。
2)预测 用偶数号序列Ei-1的预测值Pred(Ei-1)预测奇数号序列Oi-1,将预测算子Pred对偶数号序列作用后所得的值作为奇数号序列的预测值,奇数号序列的实际值与预测值相减得到残差信号。用Pred(Ei-1)与Oi-1的差代替原来的Di-1,所得的Di-1表示信号的细节信息。
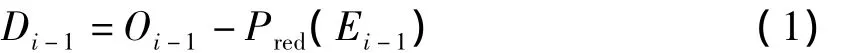
3)更新Si-1是经分解后得到的逼近信号,为了在逼近信号中保持原始信号的某些全局特性,其中最重要的是使其均值等于原信号Si的均值,不随i的变化而改变,需对其更新。构造一个算子Upd,用信号细节Di-1子集来更新Si-1,采用公式(2)。
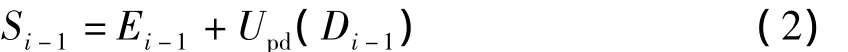
若对分解得到的逼近信号Si-1再进行以上步骤的分解即可得到原始信号的一个多级分解。
重构过程包括反更新、反预测和合并三个步骤。
1)反更新 给定Si-1和Di-1,由公式(3)计算恢复偶数号序列。
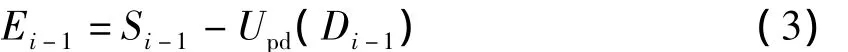
2)反预测 用反更新得到的Ei-1和给定的Di-1用公式(4)计算得到奇数号序列。
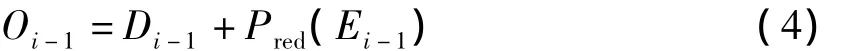
3)合并将恢复得到的奇数号序列和偶数号序列合并得到原始信号。合并表达式如(5)式所示。

式中Merge表示合并算子。
2.2 RLS 算法
RLS算法,用于设计自适应的横向滤波器,递推更新滤波器抽头权系数。以下根据文献[14,17]RLS算法作简要的介绍。
假设j时刻输入x(j),期望信号为d(j),则作为代价函数的指数加权的误差平方和如(6)式所示:
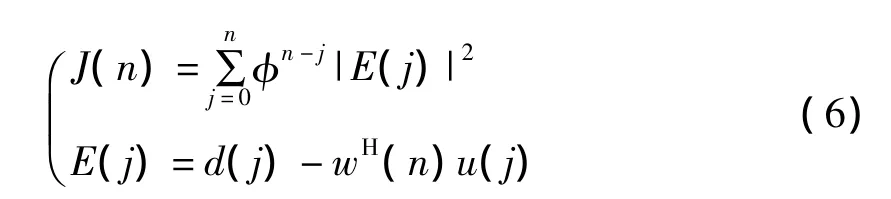
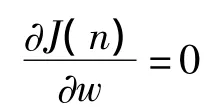
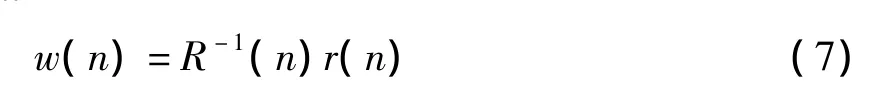
根据矩阵的求逆引理,可得R-1(n)的递推公式

定义增益向量为
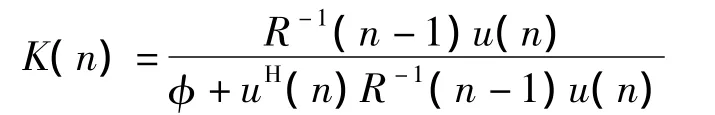
根据互相关矩阵r(n)、R-1(n)和w(n)可以求得
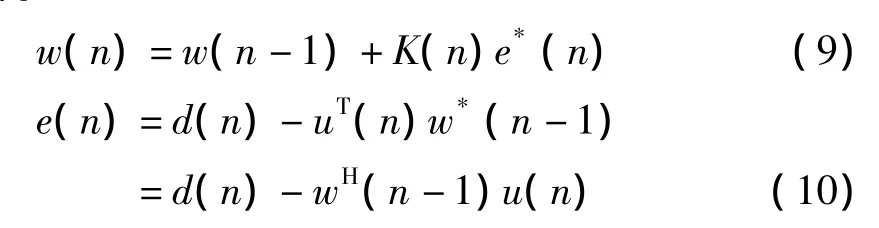
令P(n)=R-1(n),RLS直接算法的基本步骤如下:
A.初始化w(0)=0,P(0)=σ-1I,其中σ是一个极小的数值;
B.更新计算滤波器系数按照下列式子迭代计算:

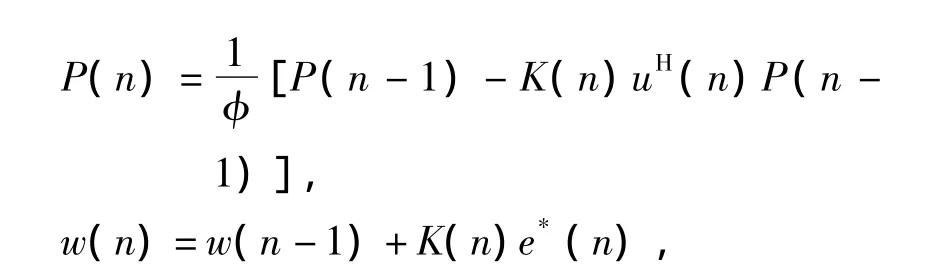
由此迭代更新滤波器系数。
2.3 基于提升小波与RLS的涡轮泵故障检测
涡轮泵由于工作在高压、高负载荷、温度条件极端等恶劣环境中,承受来自自身振动和发动机其它振源的强烈振动的影响,故障发生概率较高且危害极大[2]。通过分析涡轮泵的缓变参数(如温度、压强等)和速变参数(振动位移信号、振动加速度信号等)可以监控其故障情况。振动信号富含涡轮泵工作状态的信息,且对涡轮泵的状态信息反映十分迅速、敏感,因此本文选择涡轮泵的壳体振动加速度信号进行检测分析。
涡轮泵的振动信号通常表现出非严格平稳特性,尤其在故障发生后非平稳性更突出。小波是分析非平稳信号的良好工具,它在机械故障检测与诊断中取得较好效果[18-20]。提升小波继承第一代小波的优点,而且其直接在时域或空域构造小波,具有计算速度快、易于硬件实现等特点。因此本文以提升小波变换为基础提取故障特征。
由于发动机涡轮泵工作条件复杂,其振动信号受随机因素的影响严重,呈现非线性、非平稳性,有必要对提升小波变换提取的故障特征序列进一步处理。鉴于RLS的优点,采用RLS算法对故障特征序列进行滤波和分析。
2.3.1 故障特征提取与计算
设S是待检测信号,信号长度为L,按步长l将S划分成M个信号段Sk,k=1,2,…,M,记信号段Sk为Sk(n),n=1,2,…,l。将Sk(n)经提升小波分解和单支重构后得K层逼近信号和K层细节信号,分别记为Akj(n),j=1,2,…,K,n=1,2,…,l和Dkj(n),j=1,2,…,K,n=1,2,…,l,简记为Akj和Dkj。峭度是无量纲参数,对冲击信号特别敏感,加权平均均方根可以有效反映信号能量变化,故以此为基础计算故障特征。
1)基于逼近信号的故障特征加权平均峭度用公式(11)和(12)来计算。
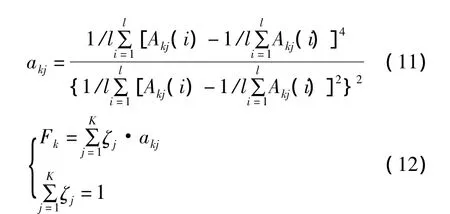
其中峭度影响系数 ζj∈[0,1],表示各层信号的峭度序列对逼近信号整体峭度序列的影响系数,可根据各层信号对工作状态的反映能力调整ζj大小,akj表示第k步的第j层逼近信号的峭度,Fk表示逼近信号的第k步的加权平均峭度。得到逼近信号的故障特征序列为(F1,F2,…,Fk,…,FM)。
2)基于细节信号的故障特征用公式(13)和(14)来计算。
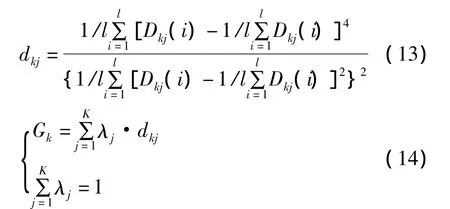
其中峭度影响系数λj∈[0,1],λj表示第j层细节信号对细节信号整体的影响系数,dkj表示第k步第j层细节信号的峭度,Gk表示细节信号的第k步的加权平均峭度。获得细节信号的故障特征序列为(G1,G2,…,Gk,…GM)。
3)基于低频逼近信号与细节信号的故障特征用(15)、(16)和(17)计算。

其中 ψj∈[0,1],均方根加权系数 ψj反映第j层信号对整体的影响程度的比例,Vkj(j>0)和Vk0分别表示第k步第j层细节信号和第K层逼近信号的均方根,Wk表示细节信号与第K层逼近信号的第k步的加权平均均方根。得到细节信号与第K层逼近信号的故障特征序列为(W1,W2,…Wk,…WM)。提取了基于逼近信号和细节信号的故障特征后,即可将其用于RLS算法滤波和进行故障检测。
2.3.2 故障判别决策
将提取的基于逼近信号与细节信号的加权平均均方根序列作为RLS算法的分析对象,采用RLS直接算法滤波。设输出的故障特征(经RLS处理后的加权平均均方根和加权平均峭度)当前时刻值为Y(n),前N个时刻的实际故障特征值为X(n),…,X(n-N+1)。故障判别计算如式(18)和(19)所示:
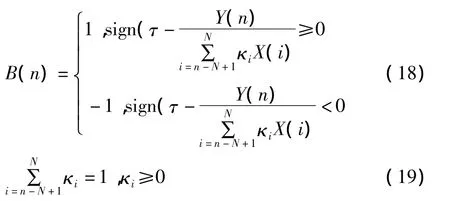
其中τ是滤波输出的当前特征点与其邻近特征值的加权平均的比值阈值,其满足 τ∈(1,+∞),B(n)表示故障报警标号(B(n)为1时表示正常,为-1时表示异常),加权系数κi表示邻近特征点影响均值的程度。
在判定某一特征序列故障时,若连续n步内有(n-1)步检出异常,则判定该故障特征序列检出故障。本文采用3个故障特征序列,若有两个或两个以上的特征序列报故障,则判定系统故障。
2.3.3 故障检测流程
基于提升小波与RLS的涡轮泵故障检测方法的实现主要有以下几个步骤:
第一步,初始化相应的参数,将原始信号按照设定的检测步长进行分段,将每步信号用提升小波变换进行分解和单支重构,利用公式(11)~(17)计算基于逼近信号和细节信号的故障特征(逼近信号与细节信号加权平均均方根、逼近信号的加权平均峭度和细节信号的加权平均峭度)。
第二步,利用RLS直接算法对加权平均均方根序列滤波。
第三步,利用故障判别计算公式(18)和(19)计算判定故障特征序列是否异常,采用给出的故障判别决策综合判定系统故障情况,以检测涡轮泵的故障。
3 实验验证
为验证故障检测方法,本文选择某型涡轮泵壳体的7段振动加速度信号(正常信号段NT1、NTr1、NTr2、NTr3 和故障信号段 FT1、FTr1、FTr2)作为试验对象,7段信号均为模拟信号。将信号段NT1和FT1作为故障特征提取的分析信号;另外的6段信号被用于模拟涡轮泵稳态工作过程的故障检测。
3.1 故障特征的分析验证
为了分析故障特征对涡轮泵故障的敏感性和稳定性,试验中选取正常的信号段NT1和故障信号段FT1,其中NT1时长为19 s,FT1时长为20 s。试验中设定检测步长为25 ms。用本文的故障特征计算方法提取信号的故障特征序列。图1是对正常信号段NT1提取的细节信号和逼近信号的加权平均峭度特征序列,以及细节信号与逼近信号的故障特征序列。图2是对信号段FT1提取的细节信号和逼近信号的加权平均峭度序列,以及细节信号与逼近信号的故障特征序列。以下如无特别说明,图中的Fk Sequence和Gk Sequence分别表示逼近信号和细节信号的加权平均峭度特征序列,Wk Sequence是加权平均均方根特征序列。
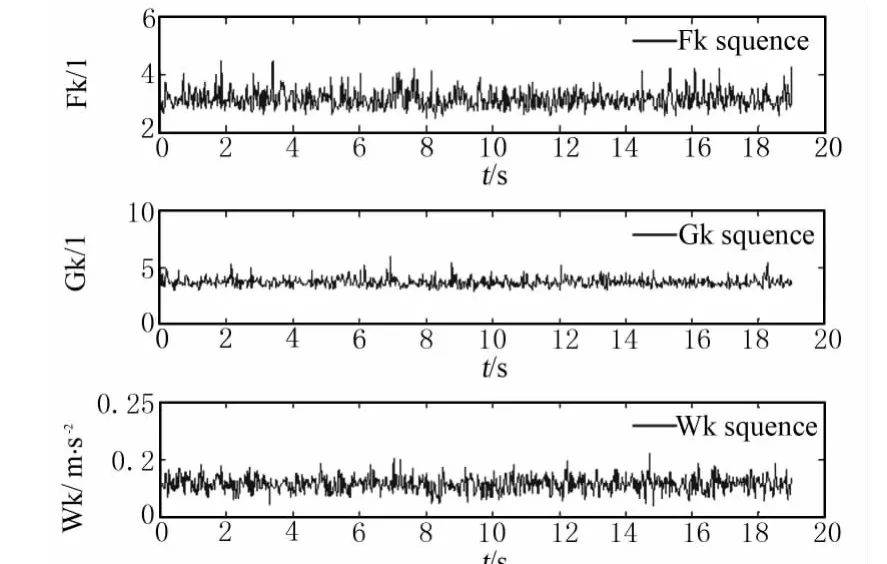
图1 NT1提取的故障特征序列Fig.1 Fault feature sequences extracted from NT1
从图1可知,正常信号的故障特征序列(Fk Sequence,Gk Sequence和 Wk Sequence)总体上呈现平稳波动趋势,可是其波动幅度偶尔出现较大但呈现不连续的情况。从图2可知,故障信号FT1的故障特征序列在未出现故障前呈现平稳波动,但当出现故障后其幅值陡然增长。试验对其它历史数据的分析也得到类似的结果,说明本文方法提取的故障特征具有较好的故障敏感性,但正常信号的分析结果,即故障特征序列仍存在序列不平缓,部分正常偶尔波动较大的问题,这使检测易出现虚警,需要结合一定的判定策略以减少虚警。
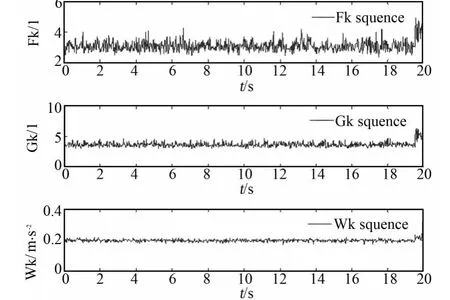
图2 FT1提取的故障特征序列Fig.2 Fault feature sequences extracted from FT1
3.2 故障检测方法的有效性和实时性验证
正常信号段NTr1、NTr2、NTr3和故障信号段FTr1、FTr2被用于模拟涡轮泵的实时故障检测过程,以验证本文方法的有效性和实时性。
3.2.1 检测方法的有效性验证
为验证方法的有效性,作为试验对象的信号为NTr1和FTr1,NTr1是时长为16 s的正常信号,FTr2是时长21.0177 s的故障信号。根据对故障信号的试车后数据分析,已知信号在20.5102 s出现故障。图3是对NTr1故障检测的结果,图4是对FTr1故障检测的结果。
从图3可知该检测方法在检测正常数据过程中没有出现报警情况,图4结果显示检测方法对信号FTr1检测,加权平均峭度在20.6 s时报警,加权平均均方根在20.9750 s报警。检测过程未出现虚警和漏警,说明本文方法在故障检测中是有效的。
3.2.2 检测方法的实时性验证
为分析检测方法的实时性,用信号段NTr1、NTr2、NTr3、FTr1和FTr2对本文方法进行验证分析,检测结果如表1所示。
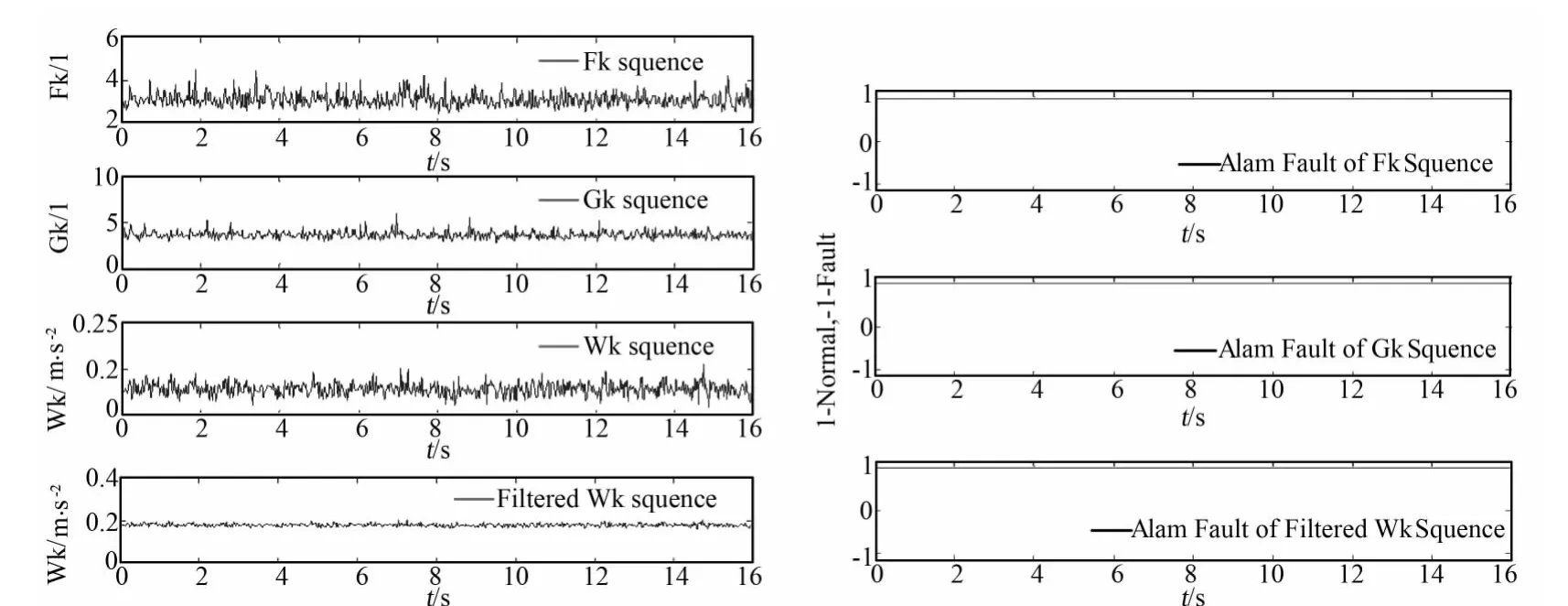
图3 故障检测方法对NTr1检测的结果Fig.3 The fault detection results of NTr1 with the proposed method

图4 故障检测方法对FTr1检测的结果Fig.4 The fault detection results of FTr1 with the proposed method
从表1可知,在检测中每步长信号计算时间均比步长时间少,因此不会出现运算时间的累积大于信号时长的情况,能够实时检测实时采集的数据。在检测故障数据时能有效检测故障,进行故障报警。说明方法有较好的实时性。试验中,采用给出的故障判别决策后,本文方法在检测正常数据时未出现虚警,在检测故障信号时未出现虚警和漏警,说明其在故障检测中具有较好的准确性。
4 结论
本文提出了一种基于提升小波与RLS的涡轮泵故障检测方法,通过某型发动机涡轮泵历史试车的壳体振动加速度信号验证故障检测方法。由试验结果,可得以下结论:1)本文方法能有效检测发动机涡轮泵的故障,在故障检测中未出现虚警和漏警,具有良好的准确性和实时性;2)在故障特征计算中采用提升小波进行信号的分解和重构,方法简洁、计算速度快、原位运算节省存储空间,提高了运算效率;3)采用RLS算法对故障特征进行滤波,减少了由随机因素引起的故障特征过大波动,减小虚警和漏警;4)提出了一种故障特征计算提取方法,用提升小波变换对信号进行分解和单支重构,计算逼近信号与细节信号的加权平均均方根、加权平均峭度作为故障特征,故障特征稳定性较好,故障敏感性较强,能有效反映涡轮泵的状态变化;5)在故障判别策略中,计算当前特征点与其邻近局部均值的比值,将其与设定的阈值对比,采用连续多次异常则进行特征序列报警,根据多个特征序列报警来判定涡轮泵故障,有效减少了虚警。

表1 检测五组涡轮泵壳体振动加速度信号的实验结果Table 1 Fault detection results of 5 groups of vibration acceleration signals of shell of turbopump
本文为涡轮泵的健康监控提供了一种故障检测方法,对故障检测与诊断具有一定的意义。然而对于故障检测方法的软、硬件系统实现和应用,故障判别策略中的比值阈值的设置和更新调整方面还需进一步研究。
[1] 陈启智.液体火箭发动机故障检测与诊断研究的若干进展[J].宇航学报,2003,24(1):1-11.
[2] 夏鲁瑞.液体火箭发动机涡轮泵健康监控关键技术及系统研究[D].长沙:国防科学技术大学,2010,1-19.
[3] 谢光军,胡海峰,秦国军,等.液体火箭发动机涡轮泵健康监控系统[J].国防科技大学学报,2005,27(3):40-44.
[4] 贺菲.运载火箭故障检测处理系统软件研究和实践[J].载人航天,2008(2):28-32.
[5] 彭小辉,刘垠杰,程玉强,等.基于云关联规则的液体火箭发动机实时故障检测方法[J].载人航天,2013,19(3):84-90.
[6] 张惠军.液体火箭发动机故障检测与诊断技术综述[J].火箭推进,2004,30(5):40-45.
[7] 谢光军,李俭川,胡茑庆,等.涡轮泵实时故障检测的多特征参量自适应阈值综合决策算法[J].中国机械工程,2005,16(13):1184-1187.
[8] 谢光军,胡茑庆,温熙森,等.涡轮泵实时故障检测短数据均值自适应阈值算法[J].推进技术,2005,26(3):202-205.
[9] 谢廷峰,刘洪刚,丁伟程,等.液体火箭发动机基于ATA算法的实时故障检测与报警系统实现[J].火箭推进,2005,31(6):19-22.
[10] 洪涛,黄志奇,钟福利.涡轮泵实时故障检测的频段幅值最大值比方法[J].电子测量与仪器学报,2012,26(1):24-30.
[11] Xia Lu-Rui,Hu Niao-Qing,Qin Guo-Jun,et al.Typical fault diagnosis method for high-speed turbopump of Liquid Rocket Engine[C]//Systems and Control in Aerospace and Astronautics,2008.ISSCAA 2008.2nd International Symposium on Shexzhen,2008:1-5.
[12] 罗俊,何立明,陈超.基于小波分形和一类辨识的航空发动机故障诊断[J].推进技术,2007,28(1):82-85.
[13] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2004:358-370.
[14] 张贤达.现代信号处理[M].北京:清华大学出版社,2002:206-213.
[15] Sweldens W.The lifting scheme:a construction of second genneration wavelets[J].SIAM Journal on Mathematical Analysis,1997,29(2):511-546.
[16] Sweldens W.The lifting scheme:a custom-design construction of biorthogonal wavelets[J].Applied and Computational Harmonic Analysis,1996,3(2):186–200.
[17] 石敏,吴正国,尹为民.基于RLS算法的时变谐波检测[J].电工技术学报,2005,20(1):50-53.
[18] He Zhengyou,Fu Ling,Lin Sheng,et al.Fault detection and classification in EHV transmission line based on wavelet singular entropy[J].IEEE Transaction on Power Delivery,2010,25(4):2156-2163.
[19] 樊春玲,金志华,田蔚风.基于小波模糊神经网络的陀螺仪故障诊断技术[J].上海交通大学学报,2003,37(1):141-144.
[20] 叶昊,王桂增,方崇智.一种基于小波变换的导弹运输车辆故障诊断方法[J].自动化学报,1998,24(3):301-306.
