对常微分方程求解及图像性质的分析

周晨星，张重阳，琪木格

（长春师范学院数学学院，吉林长春 130032）

对常微分方程求解及图像性质的分析

周晨星，张重阳，琪木格

（长春师范学院数学学院，吉林长春 130032）

本文对常微分方程的解的存在性和解析式进行研究，通过软件matlab对常微方程的解析式进行验证。针对复杂的常微分方程不仅用matlab求解，而且用图形显示出数值解，通过图像去分析解的合理性。

常微分方程的解；matlab求解；解的性质与图像

常微分方程在应用和理论上都特别重要，求常微分方程解的方法也很多，常见的方法有常数变易法、待定系数法、Laplace变换法、算子法、Lagrange变动参数法、特征根法等。但是，有时在解一些方程时也非常麻烦。我们可以通过matlab方法来求方程的解析解，然后对一些复杂的方程进行求解和作图，这种方法比较简单，也免去了繁杂的计算过程。

matlab符号工具箱提供了一个线性常系数微分方程的函数dsolve，这个函数允许用字符串的形式描述微分方程及初值、边值条件，最终得出微分方程的解析解。函数dsolve输入参变量由三部分组成：常微分方程、初始条件以及自变量，分别用单引号括起来，再用逗号隔开。函数的调用格式为y=dsolve(’常微分方程1’,’常微分方程2’,’…’,’初始条件1’,’初始条件2’,’…’,’自变量’)用字符串表示常微分方程，自变量缺省时为t，D表示一阶导数，D2表示2阶导数，依此类推,y返回解析解。

例1 求一阶微分方程的(x-2y)y′=2x-y解析解.

先用matlab软件求解：desovle(‘(x-2*y)*Dy=2*x-y’,‘x’)

输出结果:x*x-x*y+y*y=C，即x2-xy+y2=C.

再验证 x2-xy+y2=C 两边对 x求导，2x-y-xy′+2yy′=C.

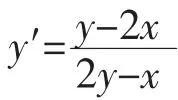
所以x2-xy+y2=C是方程(x-2y)y′=2x-y的解.

例 2 求二阶微分方程 (xy-x)y′′+xy′2+yy′-2y′=0 的解析解。

先用matlab软件求解：y=desovle(‘(x*y-x)*D2y+x*Dy^2+y*Dy-2*Dy=0’).输出结果：y=log(x*y)，即 y=ln(xy).

上式两边对 x 求导，yy′+xy′+xyy′′=2y′+xy′′.

整理得（xy-x）y′′+xy′2+yy′-2y′=0.

所以 y=ln(xy)是方程(xy-x)y′′+xy′2+yy′-2y′=0 的解.

对于复杂的方程，matlab提供了几个专门用于求解常微分方程的函数，设计思想基于Runge-Kutta方法，基本设计思想为：从改进的欧拉方法比欧拉方法精度高的缘由着手，若在区间[x1,xi+1]多取几个点的斜率值，再求取平均值，则可以构造出精度更高的计算方法，这些函数主要包括:ode45、ode23、ode15 s、ode113、ode23s等。其中最常用的是函数ode45，该函数采用变步长四阶五阶Runge-Kutta法求数值解，并采用自适应变步长的求解方法，即当解的变化较慢时采用较大的计算步长，从而使得计算速度很快，当方程的解变化得较快时，积分步长会自动变小，从而使得计算的精度很高，但是不适合刚性方程组求解。ode23采用二阶三阶Runge-Kutta法求数值解，与ode45类似，只是精度低一些。ode15s用来求刚性方程组.ode45函数的调用格式为:[tout,yout]=ode45(’yp rime’,[x0,xf],y0)，其中yprime是表示f(t,y)的M文件名，x0表示自变量的初始值，xf表示自变量的终值，y0表示初始向量值。输出向量tout表示节点(x0；x1；…；xn)，输出矩阵yout表示数值解。有了这些参数，就可以调用ode45函数对系统直接进行仿真了，在仿真结束后当然可以调用plot函数来绘制出仿真的结果曲线。

例3 求解微分方程初值问题

的数值解，求解范围为区间 [0，0.5]。

图1 例3仿真曲线

例4 求解微分方程

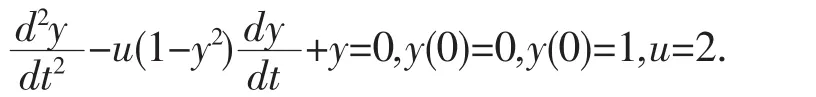
令 x1=y，x2=dx1/dt，则 dx1/dt=x2,dx2/dt=u(1-x1^2)x2-x1.

先编写函数文件verderpol.m:

再编写命令文件vdpl.m:

输出结果为

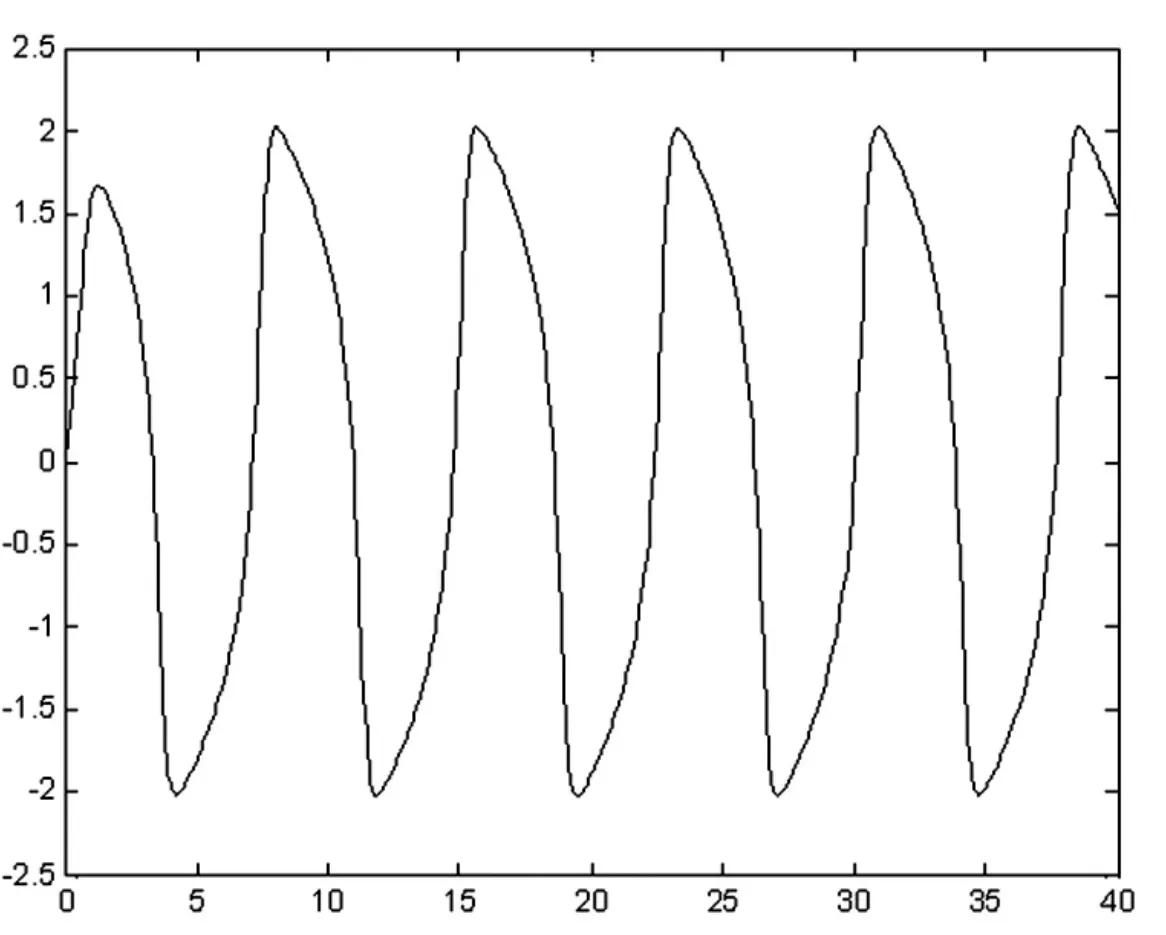
图4 例4仿真曲线

[参 考 文 献]

[1]刘仁云,张小丽,梁四化,等.数学建模方法与数学实验[M].北京:中国水刊水电出版社,2010.

[2]陈永胜,任燕.基于MATLAB求解常微分方程[J].通化师范学院院报,2008(4):103-105.

[3]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2004.

[4]刘卫国.MATLAB程序设计教程[M].北京:中国水利水电出版社,2003.

[5]李俐玲.关于数学问题的MATLAB实现方法[J].四川师范大学学报:自然科学版,2003(6):657-660.

[6]刘人丽.MATLAB中的方阵幂[J].四川师范大学学报:自然科学版,2004(2):213-215.

On the Solutions of Ordinary Differential Equations and Image Properties

ZHOU Chen-xing，ZHANG Chong-yang，QI Mu-ge
(College of Mathematics，Changchun Normal University,Changchun Jilin 130032,China)

In this paper,we study the existence of the solution of ordinary differential equations and analytic formula,and then verify software matlab analytic formula for Ordinary Differential Equations.We solve complex ordinary differential equations by matlab,display numerical solution by graph,and analyze the reasonableness of the solution by figure.

the solutions of ordinary differential equation;solving by matlab;the property and figure of solution

O175

A

1008-178X(2013)01-0001-03

2012-11-29

吉林省教育厅“十二五”科学技术研究项目（吉教科合字[2013]第252号）；吉林省2012年“大学生创新创业训练计划”项目。

周晨星（1962-），女，吉林长春人，长春师范学院数学学院副教授，从事应用数学研究。