处理两体问题的拉格朗日方法实例分析

郭俊华

（运城学院物理与电子工程系，山西运城 044000）

处理两体问题的拉格朗日方法实例分析

郭俊华

（运城学院物理与电子工程系，山西运城 044000）

两体问题一直受到人们的关注。本文对采用拉格朗日方法处理两体问题的理论作了详细阐述，并给出应用这一方法解决具体问题的实例分析。

两体问题；拉格朗日函数；广义坐标

两体问题是指由两个质点或物体组成的力学系统在仅仅受到内力作用下的动力学问题。两体问题不仅是最简单的质点系力学问题，也是唯一一例在质点系力学中被彻底解决的问题。处理两体问题时，总的运动可以看成是质心的运动和相对于质心的运动这两部分的合成。由于两体之间的相互作用是内力，不会影响质心的运动，因此，如果不存在外场，则质心做惯性运动；若还考虑外场作用，那么质心的运动应该由质心运动定理决定。所以质心运动部分可认为是已知的，关键是讨论相对运动部分。

两体问题一直受到人们的关注。统编力学教材例如理论力学具体讨论了行星-太阳系统的运动、量子力学也介绍了氢原子问题。近年来也有部分文献对两体问题进行了不同侧面的讨论。1992年范继美[1]对两体问题中的折合质量进行了讨论，给出了将两体问题约化为单体问题求解的普适方法；1994年王文科[2]对两体问题中的相对运动进行了讨论，指出了解决两体问题时比较简便的坐标系的建立方法，并从理论上进行了简单的阐述；1997年白静江[3]讨论了两体问题中的功能原理及机械能守恒定律，并阐述了它们的应用；2001年梁志强等人[4]选用质心坐标系对两体问题进行讨论，给出了有关两体问题的动力学方程并展开讨论；2008年李银山[5]首次采用分析力学中的拉格朗日方程来处理两体问题，为两体问题的研究提供了新的方法。本文将对两体问题的拉格朗日处理方法给出系统的理论分析，并结合具体实例来理解这一方法的物理含义。

1 两体问题的拉格朗日函数

对于质量为M和n的两粒子组成的系统(图1)，C为它们的质心。质心坐标表示为：

两粒子的自由度为6，取和为广义坐标。系统相对于惯性坐标系的动能为：

体系的势能只考虑两粒子的相互作用势能，此势能只与两粒子的相对位置有关，用表示。

则体系的拉格朗日函数为：

由(1)和(2)式可解得：

将(5)式代入(4)式整理得：

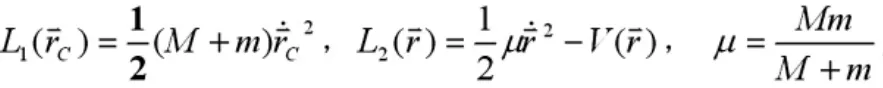
选取质心坐标和两粒子间的相对位矢 为广义坐标后，两体问题的拉格朗日函数分解为反映质心运动的拉格朗日函数和反映两粒子间相运动的拉格朗日函数两个独立的部分。这样就把两体问题分解为两个单粒子问题。

图1 两体问题图示

图2 例题示意图

2 实例应用

例 质量m1及m2为及的两质点互相以力吸引，引力与其质量成正比，与距离平方成反比，比例常数为k。试讨论两质点的运动情况。

解 两质点间仅受引力作用，则此体系为保守系，可利用保守系下拉格朗日方程求解。建立如图2所示的坐标系，选择体系的质心坐标xC及两质点间的相对坐标x为广义坐标。

则体系的拉格朗日函数为：

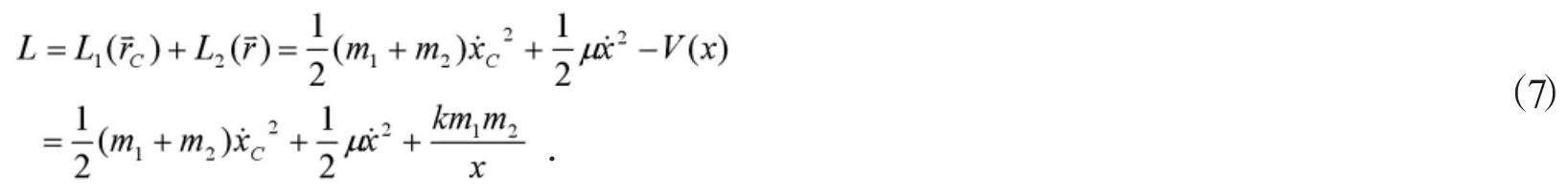
拉格朗日方程为：

将拉格朗日函数(7)分别代入拉格朗日方程(8)中解得：

其中，(9)式表明体系的质心加速度为零，质心做惯性运动，这一点从牛顿力学很容易看出，因为体系不受外力作用。(10)式是质量为μ的“质点”的动力学方程，这就把两体问题简化为单体问题。

3 结论

拉格朗日方法处理两体问题与牛顿力学方法类似，都是将两体问题简化为单体问题。但是此方法的引入可以为两体问题的处理提供更为广阔的思路，也为多体问题的解决奠定了基础。

[参 考 文 献]

[1]范继美.两体问题中的折合质量[J].昆明工学院学报,1992,17(2):121-128.

[2]王文科.关于两体问题中相对运动的讨论[J].工科物理,1994(2):19-21.

[3]白静江.两体问题中的功能原理及机械能守恒定律[J].大学物理,1997,16(3):11-14.

[4]梁志强,唐文校.质心坐标系中的两体问题[J].泰安师专学报,2001,23(3):54-57.

[5]李银山.采用拉格朗日方法来处理两体问题[J].科技创新导报,2008(6):137.

An analysis of Actual Example to Deal with Two-particle System by Lagrange Method

GUO Jun-hua

(Department ofPhysics and Electronics Engineering,YunchengUniversity,YunchengShanxi 044000,China)

The problem of two-particle system has been subject to attention.In this paper,the theory to deal with two-particle system by Lagrange method has been given in detail,and an analysis of actual example also has been given.

two-particle system;Lagrange function;generalized coordinates

O316

A

1008-178X(2013)01-0011-03

2012-11-12

郭俊华（1979-），女，河南鹤壁人，运城学院物理与电子工程系讲师，硕士研究生，从事超快光学研究。