作大范围运动FGM矩形薄板的动力学特性研究*

黎亮 章定国† 洪嘉振

(1．南京理工大学理学院，南京 2 10094)(2．上海交通大学工程力学系，上海 2 00240)

作大范围运动FGM矩形薄板的动力学特性研究*

黎亮1章定国1†洪嘉振2

(1．南京理工大学理学院，南京 2 10094)(2．上海交通大学工程力学系，上海 2 00240)

对作大范围运动功能梯度材料矩形薄板的刚柔耦合动力学问题进行了研究．以连续介质力学为基础，在柔性薄板面内变形中考虑了传统建模方法忽略的二次耦合变形量，采用假设模态法对薄板变形位移进行离散，运用拉格朗日方程推导了大范围运动功能梯度材料板的刚柔耦合动力学方程．对旋转运动下取不同功能梯度指数的悬臂功能梯度板的动力学行为进行仿真，比较了本文建立的一次近似耦合模型和传统不计耦合变形项的零次近似模型．结果表明，随着转速的提高，传统零次模型发散，而本文模型收敛，能够较好地描述系统动力学行为．利用本文建立的一次近似模型，研究了功能梯度指数对转动功能梯度板变形的影响，研究表明，随着功能梯度指数的增大，板的横向变形也增大．通过求解旋转FGM板在恒定转速下的固有频率，进一步分析了功能梯度板材料组分变化对板振动特性的影响．

大范围运动， 功能梯度材料板， 功能梯度指数， 动力刚化， 固有频率

引言

功能梯度材料(Functionally Graded Materials，简称FGM)是一种近期发展的新型功能材料，它一般是由几种不同材料介质沿空间按不同组分复合而成，形成材料功能的梯度分布，从而满足构件不同部位对材料使用性能的不同要求．由该种材料制成的功能梯度构件在空间上呈连续变化，不存在明显的界面和性能突变，具有明显优于一般复合材料的特性［1］．同复合材料结构一样，功能梯度构件在航空航天工业中具有广泛的应用．目前，有关功能梯度材料中的弹性力学分析大部分集中在静态和准静态的研究，其结构的动态响应问题在理论研究和实际应用中具有深远的意义．

自从Kane［2］揭示了“动力刚化”现象以来，国外很多学者研究了板的“动力刚化”问题［3－5］．在国内，洪嘉振、刘锦阳［6］根据连续介质力学中关于柔性薄板的变形理论，基于Jourdan速度变分原理，对板的动力学响应进行了仿真，并将有限元法和假设模态法的计算结果进行了对比．这些工作主要集中在考虑各向同性板的情况，考虑板在各向异性情况下的“动力刚化”的研究工作还比较少．Maria Augusta Neto［7］建立了复合材料层合板的多体系统刚柔耦合动力学方程，分析了其中柔性体变形与刚体运动的耦合动力学问题．Yoo［8］对转动下的复合悬臂板的模态进行了分析．吴根勇、和兴锁［9］基于经典层合板理论建立了大范围运动复合材料板的动力学方程，考虑了传统建模方法忽略的二次耦合变型量，仿真比较了层铺角度对作大范围运动复合材料板变形影响．M．T．Piovan等［10］研究了转动功能梯度梁的动力学问题，考虑了梁的剪切变形和非线性应变位移关系，计入科氏惯性效应和几何刚化效应，推导了转动功能梯度梁的非线性动力学方程，并比较了模型非线性化与线性化的差异．然而，对作大范围转动功能梯度板的动力学问题的研究比较少见．

本文研究作大范围转动悬臂功能梯度矩形薄板的动力学问题，所研究的功能梯度矩形板的材料密度和弹性模量沿厚度梯度变化，横观各向同性，忽略温度场的影响．从连续介质力学理论出发，运用拉格朗日方程建立在空间作任意运动的柔性功能梯度薄板的刚柔耦合一次近似动力学模型．仿真了随功能梯度系数变化的功能梯度薄板作旋转运动的动力学行为，比较了计及二次耦合变形量的一次近似模型和不计二次耦合变形量的传统零次近似模型在动力学性质上的差异．通过求解FGM板在转动下的固有频率，进一步分析了功能梯度板组分变化对板模态特性的影响．

1 动力学建模

1．1 运动学描述

考虑一FGM 矩形弹性薄板，假设FGM板由陶瓷和金属两种材料介质组成，板的弹性模量E(z)和密度ρ(z)沿板的厚度呈幂函数分布，表示为［11］:

其中，N(N≥0)为功能梯度指数，h为板厚度．下标‘c’、‘m’分别代表陶瓷材料和金属材料，泊松比μc= μm=μ．板的长度为a，宽度为b．

在空间作大范围运动的FGM矩形薄板如图1所示．图中，e0为惯性坐标系，eb为连体坐标系．e0和eb(i=1，2，3)分别为惯性基和连体基的单位向量，eb1和eb2构成的坐标平面与未变形的板中面重合．

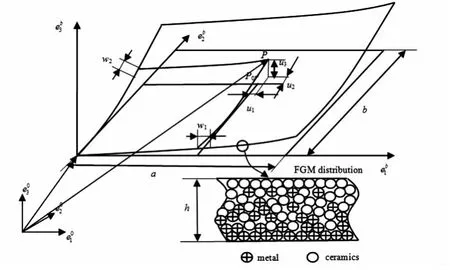
图1 作大范围运动FGM矩形板Fig．1 A FGM plate undergoing large overall motion

变形前板中面上任一点P0变形后至P点，变形矢量为u，u在连体坐标系下的分量列阵为［u1u2u3］T．P0点在面内沿x、y方向的变形位移u1、u2可表示为

式中，Vo、ωA为连体坐标系相对于惯性坐标系的速度、角速度矢量，分量列阵分别为［v1v2v3］T和［ω1ω2ω3］T，ρ0为点P0在连体坐标系中的位置矢量，VPA为P点相对连体坐标系的速度矢量．各矢量在连体坐标系的分量形式为

1．2 系统的动能和势能

FGM板的动能为

在平面应力假设下，应力为

FGM板的变形势能为

式中U1为板面内变形能，U2为面内与横向的耦合变形能，U3为横向弯曲变形能．

1．3 系统刚柔耦合动力学方程

采用假设模态法对 w1、w2、u3离散，得

式中，φi(x，y)∈R1×Ni(i=1，2，3)为功能梯度薄板面内振动和横向振动的模态函数阵，qi(t)∈RNi(i=1，2，3)为面内振动和横向振动的模态坐标列阵，Ni为对应的模态截断数．为方便起见，下述表达式中略去自变量 x，y，t．

将式(16)代入式(2)，得变量 u1，u2

式中，H1(x，y)、H2(x，y)为耦合形函数，表示如下

下标中“，”表示对坐标求偏导数．

取广义坐标q=［］T，将动能和势能代入拉格朗日方程:

得到FGM板的刚柔耦合动力学方程为

式中各分块矩阵如下

式中，a01、a02、a03为基点加速度在连体基下的分量．各常数阵为

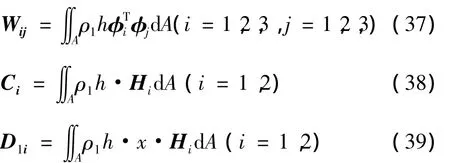
方程(20)可以模拟大范围运动已知时的功能梯度板的动力学问题．式(33)中下划线项为考虑二次耦合变形量带来的附加动力刚度项．传统的零次建模方法忽略了这些耦合项，因此零次模型中的这些项均为零．

2 数值仿真

2．1 功能梯度板“动力刚化”研究

本节仿真一作大范围旋转运动的悬臂FGM矩形薄板的动力学行为，如图2所示，中心刚体与FGM板的一端固连、分别为惯性坐标系Oxyz的单位向量，且分别与板的长、宽和厚度方向平行．中心刚体以恒定角速度ω绕y轴旋转，板的材料参数a=1．8828 m，b=1．2192 m，h=0．02 m，Ec=151 GPa，Em=70 GPa，ρc=3000 kg/m3，ρm=2707 kg/m3;泊松比取0．3，中心刚体半径R取0．ω1=ω3=0，ω2=ω==02=．给定的角速度规律为

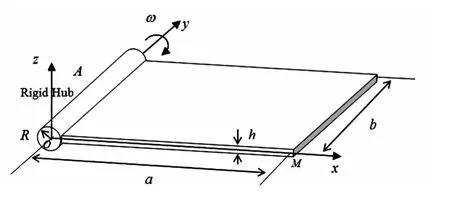
图2 作旋转运动的悬臂功能梯度薄板Fig．2 A rotating cantilever FGM thin plate

式中，T=30 s．

只考虑FGM板沿厚度方向上的横向振动，系统的动力学方程简化为

采用模态试函数方法，板的第mn阶模态试函数Zmn(x，y)可以分解为x方向悬臂梁和y方向自由梁的模态函数Xm(x)和Yn(y)的乘积，即矩形薄板的横向振动模态函数为

其中x方向悬臂梁作横向弯曲振动模态函数

Y方向自由梁作横向弯曲振动模态函数为［12］

式中，βm为方程 cos(βml)cosh(βml)= －1的第m个根，βn为方程 cos(βml)cosh(βml)=1的第n－2个根，φ3i为φ3的第i阶分量．

图3、4分别给出了板功能梯度系数N取1和2，Ω=3 Hz以及Ω=10 Hz时利用零次近似模型和一次近似模型计算得到的外侧角点M的横向变形．从图中可以看出，在Ω=3 Hz时，两种近似模型的结果差异很小，比较图3(a)、图4(a)，零次近似模型计算得到的角点最大变形均比本文一次近似模型得到的结果偏大;随着功能梯度系数的增大，零次近似模型结果与本文一次近似模型的结果差异也呈增大趋势．当Ω=10 Hz时，从图3(b)、图4(b)中可以看到，两种模型的计算结果出现了明显的差异，零次模型的结果均发散，本文一次近似模型的结果均收敛，差异来源于附加刚度项．

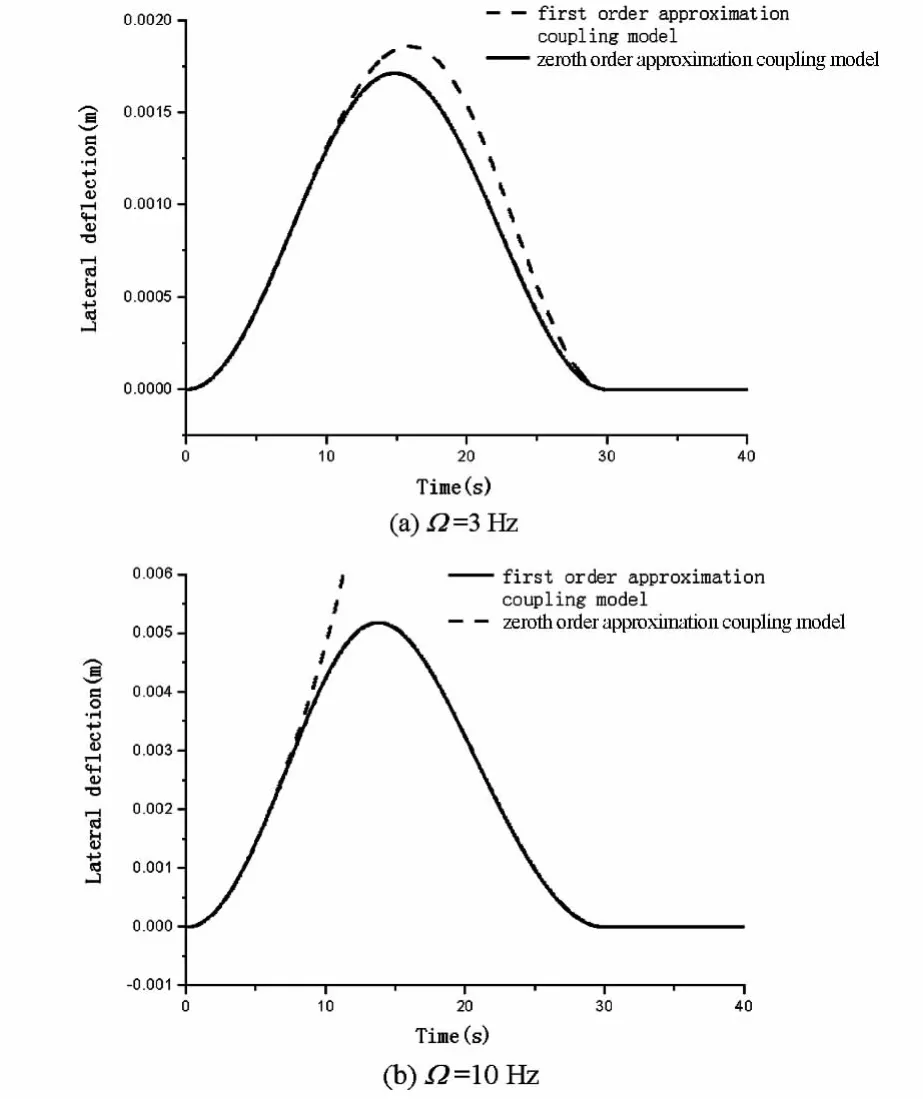
图3 N=1时板外侧角点的横向变形Fig．3 Lateral deflection of the plate＇s corner for the case of N=1

图4 N=2时板外侧角点的横向变形Fig．4 Lateral deflection of the plate＇s corner for the case of N=2

图5分别给出了Ω=3 Hz和Ω=10 Hz时功能梯度板的功能梯度系数变化下板外侧角点在z方向的变形．从图5(a)和图5(b)中可以看出，当N=0时，功能梯度板退化为均质板，板的最大变形最小，随着N的增大，板的最大变形也增大，说明功能梯度系数是改变功能梯度板柔性特性的重要原因，功能梯度系数越大板的柔性也越大．

图5 不同功能梯度系数下外侧角点的横向变形比较Fig．5 Comparison of the plate＇s corner lateral deflection with different functionally graded index

2．2 旋转功能梯度板的横向弯曲固有频率分析

本节对作匀速旋转运动的悬臂功能梯度薄板的横向弯曲固有频率进行研究，忽略面内变形对横向弯曲的影响，系统的横向弯曲振动方程可以写为:

求解方程(57)，令

其中，j为虚数，p为固有频率，Z为常数列阵．将式(58)代入式(57)得到特征方程

由于下划线部分D11为动力刚化项，式(57)仍为一次刚柔耦合模型，去掉动力刚化项，式(57)则退化为零次模型．图6为分别采用零次模型和一次模型计算所得的FGM板(N=0)横向一阶固有频率随转动角速度增加的变化对比图．从图中可以看出，当转速较低时，零次模型与一次模型计算的一阶固有频率差别不大，但随着转速增加，零次模型计算结果越来越小，不符合实际情况;相反，一次模型计算结果随转速的提高呈稳定增长趋势，能很好地体现系统的动力刚化效应．

图6 一次模型与零次模型一阶固有频率比较Fig．6 Comparison of first natural frequencies between first and zeroth order models

图7 ω=50 rad/s时FGM板各阶固有频率随N的变化情况Fig．7 Variations of natural frequencies versus N(ω =50 rad/s)

图7给出了转动角速度为50 rad/s时FGM板前八阶固有频率随功能梯度指数变化的情况，从图中可以看出，FGM板的各阶固有频率均与N成反比．图8为不同功能梯度指数的FGM板的一阶固有频率随转速的变化情况，从图中可以看出，功能梯度指数能显著改变FGM板的一阶固有频率，随着N的增大，不同转速下的一阶固有频率都呈递减趋势．

图8 不同功能梯度系数的FGM板的一阶固有频率随角速度变化情况Fig．8 First natural frequencies of FGM plate with different N changing along with angular speed

3 结论

1)建立了作大范围旋转运动的FGM板的刚柔耦合动力学一次模型，数值仿真结果证明在低速转动时，柔性薄板变形位移的耦合变形量对系统的动力学性能影响较小，然而在高速转动情况下，耦合项使得系统的刚度增大，产生动力刚化效应．一次模型不仅适应于低速的大范围转动，而且适用于高速的情况．

2)在本文中既定的功能梯度材料参数的分布规律情况下，随着功能梯度指数的增大，功能梯度板的横向变形要比各项同性板的大，在材料设计中，应适当考虑N的取值范围，以利于控制柔性板的变形．

3)功能梯度指数能显著影响旋转FGM板的横向弯曲固有频率，N越大，各阶固有频率越小，且均与转速成正比．

1 郝育新，张伟，赵秋玲．复合边界条件下功能梯度板1∶1内共振的周期与混沌运动．动力学与控制学报，2011，9(2):117～122(Hao Y X，Zhang W，Zhao Q L．Periodic and chaotic motion of mixed boundary FGM plate with 1∶1 internal resonance．Journal of Dynamics and Control，2011，9(2):117～122(in Chinese))

2 Kane T R，Ryan R R，Banerjee A K．Dynamics of a cantilever beam attached to a moving base．Journal of Guidance，Control and Dynamics，1987，10(2):139 ～151

3 Banerjee A K，Kane T R．．Dynamics of a plate in large overall motion．Journal of Applied Mechanics，1989，56:887～892

4 Boutaghou Z E，Erdman A G，Stolarski H K．Dynamics of flexible beams and plates in large overall motions．Journal of Applied Mechanics，1992;59:991 ～999

5 Yoo H H，Chung J．Dynamics of rectangular plates undergoing prescribed overall motion．Journal of Sound and Vibration，2001，239(1):123～137

6 刘锦阳，洪嘉振．作大范围运动矩形薄板的建模理论和有限元离散方法．振动工程学报，2003，16(2):175～179．(Liu J Y，Hong J Z．Dynamic modeling theory and Finite Element Method for a rectangular plate undergoing large overall motion．Journal of Vibration Engineering，2003，16(2):175 ～179(in Chinese))

7 Neto M A，Jorge A C，Ambro＇sio，Roger＇io P．Leal．Composite material in flexible multibody systems．Computer Methods in Applied Mechanics and Engineering，2006，195:6860～6873

8 Yoo H H，Kim S K，Inman D J．Modal analysis of rotating composite cantilever plates．Journal of Sound and Vibration，2002，285(2):233 ～246

9 吴根勇，和兴锁．做大范围运动复合材料板的动力学建模研究．计算力学学报，2010，27(4):667～672(Wu G Y，He X S．Dynamic modeling for a composite plate undergoing large over motion．Chinese Journal of Computational Mechanics，2010，27(4):667 ～672(in Chinse))

10 Piovan M T，Sampaio R．A study on the dynamics of rotating beams with functionally graded properties．Journal of Sound and Vibration，2009，327:134 ～143

11 Reddy J N．Analysis of functionally graded plates．International Journal for Numerical Methods in Engineering，2000，47:663 ～684

12 Rule J A，Richard R E，Clark R L．Design of an aero elastic delta wing model for active flutter control．Journal of Guidance Control and Dynamics，2001，24(5):918 ～924

* This work was supported by the National Natural Science Foundations of China(11272155，11132007，10772085)，the“333”Project of Jiangsu Province(BRA2011172)，and the Fundamental Research Funds for the Central Universities(30920130112009)

† Corresponding author E－mail:Zhangdg419@mail．njust．edu．cn

DYNAMICS OF RECTANGULAR FUNCTIONALLY GRADED THIN PLATES UNDERGOING LARGE OVERALL MOTION*

Li Liang1†Zhang Dingguo1Hong Jiazhen2
(1．School of Sciences，Nanjing University of Science and Technology，Nanjing210094，China)(2．Department of Engineering Mechanics，Shanghai Jiaotong University，Shanghai200240，China)

The rigid－flexible coupling dynamics of a rectangular functionally graded thin plate undergoing large overall motion is investigated．Based on continuum medium mechanics，The governing equations of motion are established using assumed mode method and Lagrange＇s equations，for the rectangular functionally graded thin plates undergoing large overall motions．The second order coupling deformation variable，which is ignored in traditional method，is considered in this paper．The dynamics of cantilever plates with different functionally graded coefficiernt undergoing rotation are simulated and the deformation results of first order approximation model are compared with those of traditional zero order appoximation model．It is shown that，as the rotating velocity increase，the traditional model divergences while the first order model converges．The first order model describes the dynamic behavior of the system better．The effects of the functionally graded index on the deformation of plates are studied．Studies have shown that，with the increases of the functionally graded index，the greater the lateral deformationthe of plate．By solving the natural frequencies of rotating FGM plate under a constant speed，the impact of of changes in the material composition of FGM plates on the plate vibration characteristics is further studied．

large overall motions， functionally graded plates， functionally graded index， dynamic stiffening，natural frequencies

21 July 2012，

30 August 2012．

10．6052/1672－6553－2013－042

2012－07－21 收到第 1 稿，2012－08－30 收到修改稿．

*国家自然科学基金资助项目(11272155，11132007，10772085)、江苏省“333工程”(BRA2011172)、中央高校基本科研业务费专项资金资助(30920130112009)

E－mail:Zhangdg419@mail．njust．edu．cn