分数阶微分方程积分边值问题正解的存在性

靳 威，寇春海

（东华大学 理学院，上海 201620）

分数阶微分方程积分边值问题正解的存在性

靳 威，寇春海

（东华大学 理学院，上海 201620）

研究了一类带有积分边值条件的分数阶微分方程边值问题，运用Schauder不动点定理，得到了边值问题正解存在的充分条件，改进了已有的结果，同时给出了一些实例，说明所得结果的有效性.

分数阶微分方程；积分边值问题；正解；Schauder不动点定理

近年来，分数阶微分方程积分边值问题得到广泛的关注，其在力学、物理、化学工程和经济等方面有着广泛的应用，受到国内外学者的重视［1－11］.文献［1］研究了如下分数阶微分方程边值问题：

其中：2＜α≤3，0＜λ＜2，CDα是Caputo分数阶导数；f：［0，1］×［0，＋∞）→ ［0，＋∞）是连续函数.运用Guo－Krasnoselskii不动点定理，得到了边值问题（1）的正解的存在性条件.

本文运用Schauder不动点定理，以期在更弱的条件下，保证边值问题（1）的正解的存在性，改进文献［1］的结果.

1 预备知识

给出本文用到的有关定义和引理.

定义1［2］假设f：R＋→R，f的α阶Caputo分数阶导数定义为

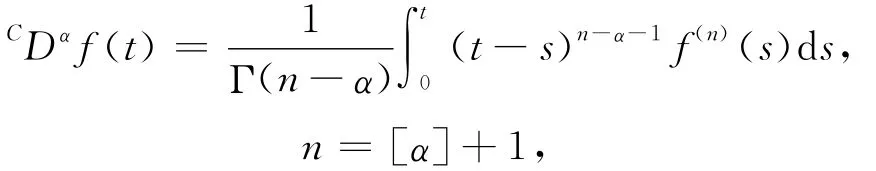
其中：α＞0，t≥0.

根据Caputo分数阶导数的定义及性质，文献［1］得到如下结果.

引理1［1］设2＜α≤3，λ≠2，p（t）∈C［0，1］，则边值问题

有唯一解

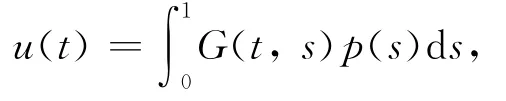
这里

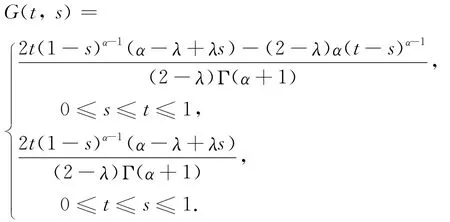
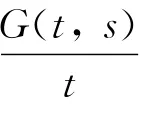
引理3［1］设2＜α≤3，0＜λ＜2，则对于任意的t，s∈［0，1］，下面的不等式成立，

本文主要运用Schauder不动点定理.

引理4（Schauder不动点定理） 设Ω是Banach空间X的一个有界凸闭集，T是Ω到其自身的全连续映射，则T在Ω内至少有一个不动点.

2 主要结果

对于任意y（t）∈C［0，1］，定义范数

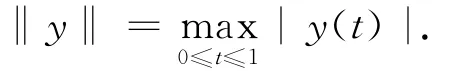
首先考虑式（3）的边值问题

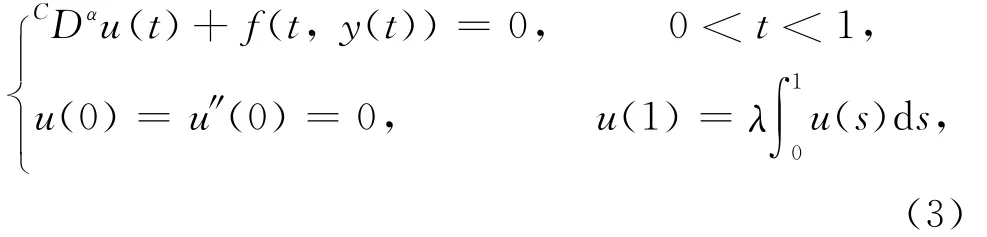
由引理1知，边值问题（3）有唯一解

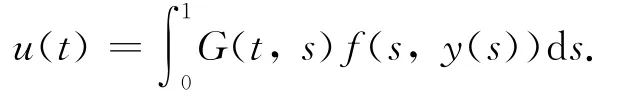
定义算子

易证，y（t）是边值问题（1）的解当且仅当y（t）是算子T的不动点，于是，问题转化为只需证明T存在不动点.

定理1 若f0＝0，则边值问题（1）至少存在一个正解.

对于y∈Ω1，由函数G和f的连续性和非负性可得，

同时，由引理2知，

由引理3知，对任意t∈［0，1］，下述不等式成立，

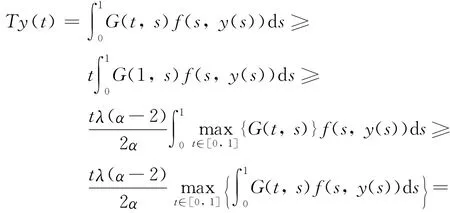
下面证明 ‖Ty‖ ≤B，事实上，由式（4）及β的定义，有

因此，TΩ1⊂Ω1.

运用与文献［1］中类似的方法，可以证明T：Ω1→Ω1是全连续的.由引理4知，T在Ω1中至少存在一个不动点，从而边值问题（1）至少存在一个正解.

注1 在文献［1］中，要求同时满足f∞＝ ∞.本文定理1去掉了这样的假设，从而改进了文献［1］的相关结果.

定理2 若f∞＝0，则边值问题（1）至少存在一个正解.

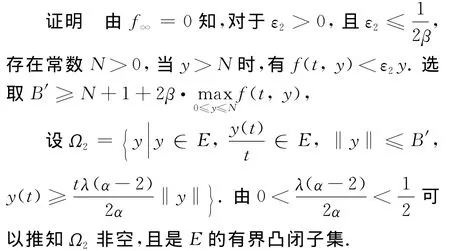
对于y∈Ω2，类似于定理1的证明，可以知道

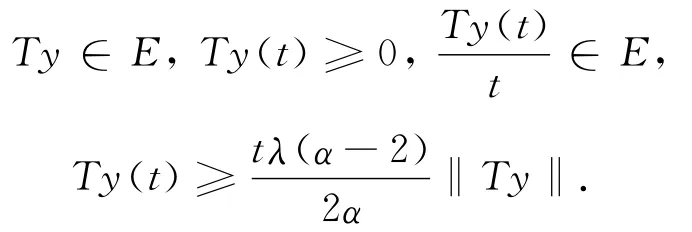
下面证明‖Ty‖≤B′，事实上，

因此，TΩ2⊂Ω2.

运用与文献［1］类似的方法，可以证明T：Ω2→Ω2是全连续的.由引理2知，T在Ω2中至少存在一个不动点，从而边值问题（1）至少存在一个正解.

注2 在文献［1］中，要求同时满足f0＝∞.本文定理2去掉了这样的假设，从而改进了文献［1］的相关结果.

运用与定理1类似的证明方法，可知T在Ω3中至少存在一个不动点，从而边值问题（1）至少存在一个正解.

运用与定理2类似的证明方法，可知T在Ω4中至少存在一个不动点，从而边值问题（1）至少存在一个正解.

3 举 例

下面给出两个例子来说明本文结果的有效性.

例1 考虑边值问题：

显然，

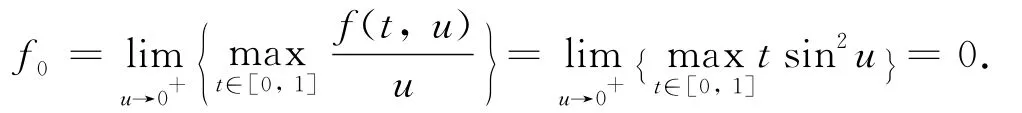
根据定理1知边值问题（5）至少存在一个正解.

例2 考虑边值问题：

参 考 文 献

［1］CABADA A，WANG G T.Positive solutions of nonlinear fractional differential equations with integral boundary value conditions ［J］. Journal of Mathematical Analysis and Applications，2012，389（1）：403－411.

［2］PODLUBNY I.Fractional differential equations［M］.London：Academic Press，1999.

［3］KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and applications of fractional differential equations［M］.Amsterdam，Holland：Elsevier，2006.

［4］ZHANG S.Positive solutions for boundary value problems of nonlinear fractional differential equations［J］.Electron J Differential Equations，2006，2006（36）：1－12.

［5］DARWISH M A，NTOUYAS S K On initial and boundary value problems for fractional order mixed type functional differential inclusions［J］.Comput Math Appl，2010，59（3）：1253－1265.

［6］AGARWAL R P，BENCHOHRA M，HAMANI S.Boundary value problems for differential inclusions with fractional order［J］.Adv Stud Contemp Math，2008，16（2）：181－196.

［7］BAI C Z.Impulsive periodic boundary value problems for fractional differential equation involving Riemann－Liouville sequential fractional derivative［J］.J Math Anal Appl，2011，384（2）：211－231.

［8］BENCHOHRA M，CABADA A，SEBA D.An existence result for nonlinear fractional differential equations on Banach spaces［J］.Bound Value Probl，2009，2009：1－11.

［9］BAI Z B，LÜ H S.Positive solutions of boundary value problems of nonlinear fractional differential equation［J］.J Math Anal Appl，2005，311（2）：495－505.

［10］SALEM H A H.Fractional order boundary value problem with integral boundary conditions involving Pettis integral［J］.Acta Math Sci，2011，31（2）：661－672.

［11］AHMAD B，SIVASUNDARAM S.Existence of solutions for impulsive integral boundary value problems of fractional order［J］.Nonlinear Anal：Hybrid Syst，2010，4（1）：134－141.

Existence of Positive Solutions for Fractional Differential Equation with Integral Boundary Value Conditions

JINWei，KOUChun－hai
（College of Science，Donghua University，Shanghai 201620，China）

A class of fractional differential equation with integral boundary value problems is investigated.By using the Schauder fixed－point theorem，some sufficient conditions are established to guarantee the existence of positive solutions for this kind of problems，which improve the known results.Furthermore，some examples are given to illustrate the advantages of the results.

fractional differential equation；integral boundary conditions；positive solutions；Schauder fixed－point theorem

O 175.8

A

1671－0444（2013）05－0695－04

2012－06－29

国家自然科学基金资助项目（10971221）

靳 威（1986—），男，河南项城人，硕士研究生，研究方向为分数阶微分方程.E－mail：jinwei1987316＠126.com

寇春海（联系人），男，教授，E－mail：kouchunhai＠dhu.edu.cn