纳米器件的分子动力学模拟

2013-09-17张晋江赵健伟

物理化学学报 2013年9期

孙玮张晋江赵健伟

(南京大学化学化工学院,生命分析国家重点实验室,南京210008)

1 引言

由于尺寸效应、表面效应等纳米材料特性的凸现,使得纳米器件的性能有别于宏观器件,因此受到学术界的广泛关注.利用纳米齿轮等器件构建纳米机械系统是纳米技术的一个重点研究方向,其中如何使器件微型化则是目前纳米器件实验研究的关键性课题.虽然已有利用电子束纳米光刻技术成功制造出纳米齿轮的相关报道,1,2但是器件的可操纵性仍有不足,而且器件的表面性质、微结构致强化等方面的实验研究也无法顺利展开.

分子动力学是一种重要的计算模拟手段,此方法主要是依靠求解牛顿力学方程来模拟分子体系的运动过程,并可进一步计算体系的部分宏观热力学性质.加之可以从原子尺度观察体系的运动,尤其是对材料形变机制的推演,可以帮助我们突破现有技术的限制,对纳米器件的性质进行预测性的研究,在一定程度上弥补了实验方法的不足.Legoas等3,4模拟研究了以多壁碳纳米管为基础构建GHz级纳米振荡器的可行性.Hwang和Kang等5,6设计了一种纳机电开关,以碳纳米杠杆在静电力影响下的弯曲度变化控制开关的闭合.Huang与Zhang7,8以及Deng和Sansoz9-11研究了通过微结构设计增强金纳米杆件性能的方法.Yang与其合作者12,13利用简化模型研究了微纳铜齿轮转动过程中的表面黏附现象以及摩擦行为等物理化学问题.本课题组的早期工作已通过分子动力学方法研究了晶向、14,15温度、16-18应变率15,19等条件对金属纳米杆件断裂行为的影响.

本文以纳米齿轮为例对具有转动性的纳米器件进行了研究.以极限转速为强度衡量标准,研究了不同尺寸的纳米器件的屈服强度以及形变机制,意在揭示尺寸效应对纳米器件强度的影响.

2 模拟方法

2.1 分子动力学模拟体系的建立

本文采用分子动力学方法对纳米级的金属铜齿轮进行了模拟.模型为直齿圆柱齿轮,采用自由边界条件,由铜单晶按渐开线齿形移除原子而得到,并选取部分原子作为轴原子,轴样式为简单键轴,轴方向为＜111＞晶向.图1所示是直径为26 nm,轴径为6.5 nm,轴向厚度(facewidth)为3.3 nm的铜齿轮,模型约包含15万个原子.分子动力学方法允许对体系中的部分原子进行标记,并对其运动速度或受力状态进行人为操控.轴原子(图1中深色原子)被标记为工具原子,可对其转动速度进行调控,其余齿轮原子(图1中浅色原子)均采取自由弛豫.

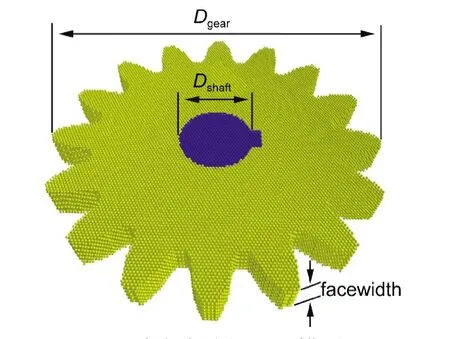
图1 纳米齿轮的原子模型图Fig.1 Atomistic model of nano-gear

在分子动力学模拟过程中,采用蛙跳算法做路径时间积分,20,21模拟步长为1.558 fs,并以Nosé-Hoover方法进行速度标定,22,23保持体系温度为10 K,自由弛豫10万步后体系达到亚稳平衡状态.利用Johnson24,25改进的解析型嵌入原子势(EAM)函数势描述铜原子之间的相互作用.其中,E代表体系总能量,V(rij)代表两个原子之间的对势能,F(ρi)代表体系中自由电子引起的嵌入能,ρi是i原子上考虑了其它所有原子作用后的电子密度;φj(rij)是j原子距离其中心rij处的电子密度.上述分子动力学模拟以及可视化显示均通过自主开发软件NanoMD完成,算法的可靠性已通过大量的实验测量和理论模拟15-17,19,26-29进行验证.

2.2 极限转速的模拟测定

本研究采用加速实验对器件的最大允许转速进行了测定.仿真实验中直接对轴原子施加角加速度,转速的差异会导致轴原子与器件原子的间距偏离平衡状态,由此产生的应力使器件原子获得加速度,从而实现了整个器件的加速转动.对轴采用了有级变速模式,每升高一级其转速增加1.00×10-7r·step-1(约为6.42×107r·s-1,对于直径为20 nm的器件,最大线速度变化量为4.03 m·s-1).由于器件原子加速的滞后性,每次轴原子加速之后都需对整个器件体系进行弛豫,通过调整弛豫时长便可以起到控制总加速度的效果.由于存在热运动扰动,单个原子的速度并不能真实反映整个体系的运动状态.我们将所有原子的线速度转换成角速度,进而统计得到体系的平均转速,跟踪此转速在整个加速过程中所能达到的最大值.

3 结果与讨论

3.1 轴加速度对器件极限转速的影响

图2为弛豫时长为2000步(约合3.12 ps,总加速度等效于2.06×1019r·s-2)时,齿轮与轴的转速-时间关系图.由于设定的有级变速模式,轴原子的转速呈阶梯状增长.如图所示,在低速阶段,非轴原子的转速会出现一定程度的振荡,但两曲线的斜率基本一致,即总体加速度相同.当转速增大至一定程度后,器件的加速度开始逐渐减小,转速到达极限转速(极大值)后开始下降.

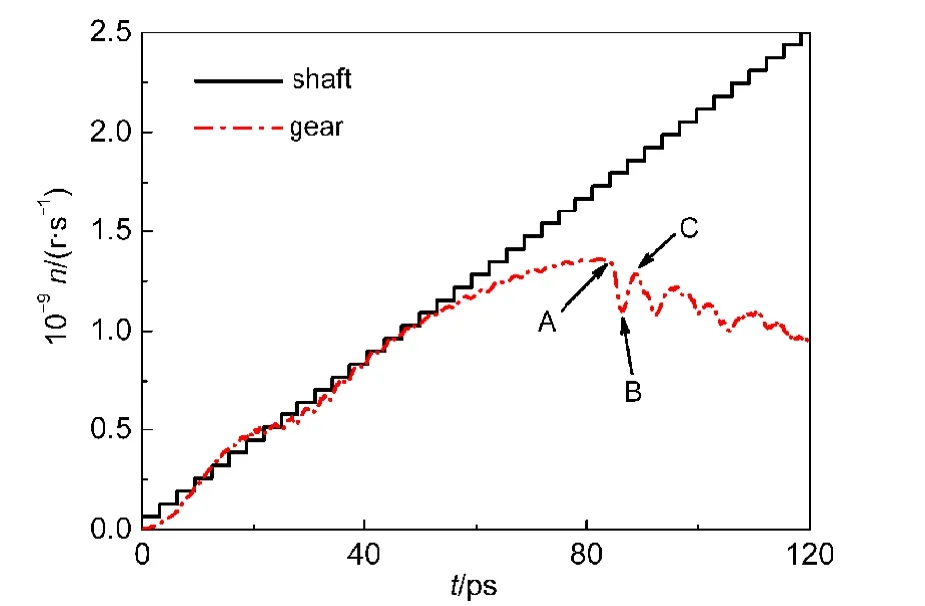
图2 轴原子与齿轮原子的转速-时间(n-t)曲线Fig.2 Rotation speed-time(n-t)curves of the shaft and gear atoms

图3 不同加速度下器件的转速-时间曲线图(A)以及极限转速与轴加速度的关系图(B)Fig.3 Rotation speed-timecurves of nano-devicewith acceleration variation(A)and the relationship between limiting rotation speed and acceleration of shaft(B)

通过将弛豫时长设定为250步至10000步,分别模拟了在从1.65×1020r·s-2到4.11×1018r·s-2的不同加速度下器件的加速过程.图3A所示为不同的轴加速度下,器件的转速随时间变化曲线.不难发现,轴的加速度会影响器件极限转速的测定.较高的加速度,弛豫时间较短,体系弛豫不足,对极限转速的影响存在两种相反的效应.一种是近轴处的弛豫不足抑制位错成核使流变应力增大,导致达到极限转速时原子的转速略有增大;另一种是外层的弛豫不足使得原子加速严重滞后,转速明显偏小,导致体系平均转速较小.当弛豫时间较小时,以后者为主导.随着弛豫时间的增长,二者同时减弱而且后者变化更显著.因此出现了极限转速的先增大后减小的现象.从图3B可以看出极限转速的测定值会随着加速度的降低而逐渐增大,当加速度达到8.23×1019r·s-2时接近平台期,当加速度小于2.06×1019r·s-2后,该测定值反而略有减小.后续模拟均采用2.06×1019r·s-2作为测试加速度.

3.2 器件的轴向厚度对其极限转速的影响

器件在整个加速实验中只发生转动,体系应变只包括圆周运动中的拉应变以及加速过程中的切应变,轴方向上不存在应变.因此体系应力只包括径向的拉应力与圆周切线方向的剪应力,而且这两种应力的大小与转速相关.根据Tresca屈服条件即体系最大切应力不变可知,随着器件转速的增加,体系应力增大到材料屈服应力后开始发生塑性形变,而发生塑性形变前的最大转速就是体系的极限转速.通过对器件原子进行缺陷分析,器件转速开始下降的时刻正是初始位错生成时刻.图4为器件在转动过快后失效过程的位错分析图,A、B、C分别对应于图2中所示的三个时刻.由图4A可以看出初始位错位置总是在器件面的靠近轴处,而且是在多个方向同时生成,之后位错沿{111}晶面进行传播.各位错面首先沿着＜112＞方向生长并在轴向上贯通整个器件,之后在＜110＞方向上继续扩展.如图4B所示各位错面交汇后会相互阻碍,在轴附近形成一个近乎封闭的区域,体系达到一个暂时稳定状态,并将再次加速.二次加速过程中部分位错面会继续生长,但程度有限,直到C时刻.由侧视图不难发现位错面在C时刻出现了一个缺口,这是由于位错层原子再次发生了滑移,两次滑移矢量叠加后相互抵消,原子又恢复了完美配位状态.

图4 器件屈服初期(图2所示三个时刻)的位错分析图Fig.4 Snapshots of dislocations in the deformed nano-device(corresponding to the three moments showed in Fig.2)

体系不存在轴向的应力,因此推测体系应力与轴向的尺寸无关,即极限转速与轴向尺寸无关.图5所示为直径20 nm,轴向厚度由1.7 nm变化到5.0 nm的一组器件的转速-时间曲线.各曲线的加速阶段基本相同,极限转速也相差甚微,只是轴向厚度较小的器件的速率振荡现象较为明显.这是由于轴向厚度与直径之比较小,原子热运动导致体系稳定性不足造成的.可见轴向厚度对器件的极限速度影响很小,这与之前的推测是吻合的.由位错演变机理可以发现轴向厚度会影响稳定态(图4B)的到来,这就是图5中各曲线的塑性阶段存在明显差异的原因.总之,在不影响体系稳定性的前提下可以采用较小的轴向厚度.

图5 轴向厚度不同的器件在相同加速度下的转速-时间曲线Fig.5 Rotation speed-time curves of devices with the same acceleration of shaft but various facewidths

3.3 器件的直径对其极限转速的影响

由初始位错位置可以推测出体系应力在临近轴处最大.周里群30以圆盘模型分析宏观齿轮在匀速转动过程中的离心应力分布,也得到了同样的结论.他发现随着质点距轴心距离的增大,切向应力是单调递减的而径向应力会先增大后减小,并且切向应力始终大于径向应力,并推测齿轮的弹性极限转速

其中σs为材料的极限应力,ρ为材料的密度,a和b分别为齿轮的轴径和直径.

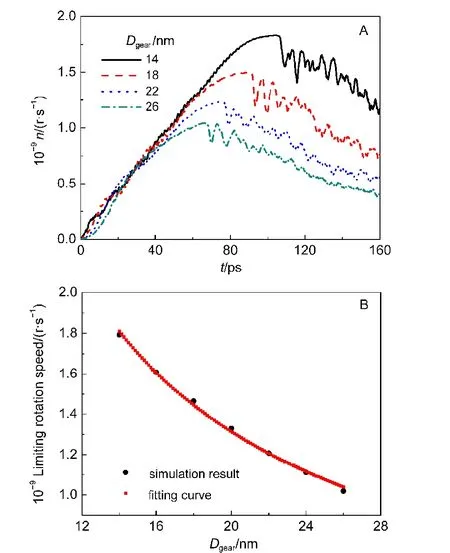
通过一系列对比实验,发现器件的直径与轴径对其极限转速确实有很大影响.图6A所示为一组轴直径均为6.5 nm,外直径由14 nm变化到26 nm的器件的转速-时间曲线,各曲线的相似度极高,只是加速范围存在差异.器件的直径越大,越早到达屈服点,极限转速也越小,极限转速与外径的关系基本符合周里群得出的结论.图6B所示为模拟结果按公式(3)进行的拟合,相关系数为0.99.此处不存在器件间的相互作用,微小偏差可能是表面效应引起的.说明宏观力学得到的解析规律在纳米尺度依然成立.由此可以得出结论,纳米器件的极限转速会随着直径的增大而减小.

3.4 器件的轴径对其极限转速的影响

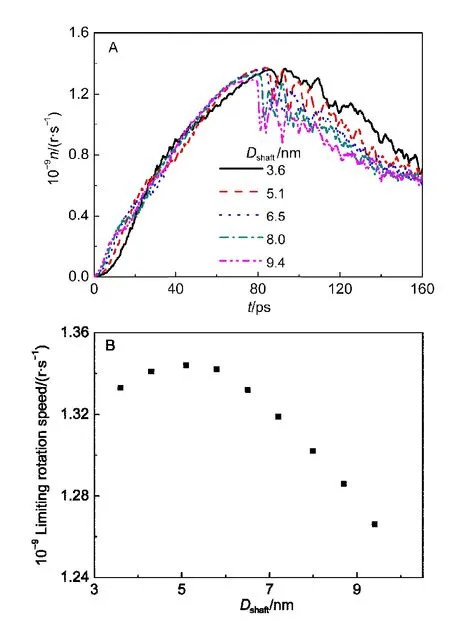
图7 轴径不同的器件在相同加速度下的转速-时间曲线(A)以及器件的极限转速随轴径的变化关系(B)Fig.7 Rotation speed-time curves of nano-devices with the same acceleration of shaft but different shaft diameters(A)and the relationship between limiting rotation speed and shaft diameter(B)

极限转速随器件轴径变化的关系与公式(3)有一定的出入.如图7A为一组外直径均为20 nm,轴径由3.6 nm变化到9.4 nm的器件的转速-时间曲线,各器件加速过程的差异较为明显.随着轴径的增大,器件的极限转速会不断减小,但变化幅度较小,说明轴直径的影响较弱,而且极限转速的变化规律也与随器件直径变化的规律不同.由图7B可以看出,极限转速随着轴径的增大会先增大后减小,在轴径为5.1 nm处(轴径与直径之比约为1:4)附近取得最大值,变化趋势类似于抛物线型.当轴径较大时,极限转速会减小,这与宏观器件的变化规律是基本相同的.但当轴径较小时,极限转速反而也会下降.齿轮轴与齿轮体之间的总牵引力实际就是两者的分界处附近的轴原子与齿轮体原子之间作用力的总合.轴与齿轮体的分界面参差不齐,作用力可以表现为吸引力和排斥力两种,排斥力可以随着间距的减小而增大至无穷,而吸引力却有极限值.初始位错点都是分布在分界面接近于{111}晶面处,这是由于{111}晶面层间原子作用力以吸引力为主,局部牵引力存在极限值,随着转速的增大容易造成局部牵引力不足而引发位错滑移.随着轴直径的下降,轴与齿轮体的分界面变小,作用力对的数目也跟着减少,而且在齿轮直径不变的前提下待驱动的齿轮体原子总数增加,相同转速下所需的牵引力也略有增加,因此更容易出现局部牵引力不足而发生屈服,最终导致极限转速有所下降.由此可见对于纳米器件,其轴径并非越小越好.

4 结论

采用分子动力学方法对以纳米齿轮为代表的可转动型纳米器件的高速转动过程进行了模拟研究.实现了极限弹性转速的测定,并通过位错缺陷分析,确定了纳米材料在高速转动下从近轴处开始形变的失效机制.研究发现纳米器件存在明显的尺寸效应,其极限转速虽与其轴向厚度无关,但会受到器件直径和轴径的影响.减小器件的直径和轴径,可以有效地提高其极限转速,但若轴径过小反而又会使其极限转速变小.这可以为纳米器件的设计提供一定的参考.

(1) Deng,J.;Troadec,C.;Ample,F.;Joachim,C.Nanotechnology 2011,22,275307.doi:10.1088/0957-4484/22/27/275307

(2)Yun,Y.J.;Ah,C.S.;Kim,S.;Yun,W.S.;Park,B.C.;Ha,D.H.Nanotechnology 2007,18,505304.doi:10.1088/0957-4484/18/50/505304

(3) Legoas,S.B.;Coluci,V.R.;Braga,S.F.;Coura,P.Z.;Dantas,S.O.;Galvao,D.S.Phys.Rev.Lett.2003,90,555045.

(4) Legoas,S.B.;Coluci,V.R.;Braga,S.F.;Coura,P.Z.;Dantas,S.;Galvao,D.S.Nanotechnology 2004,15,S184.

(5) Hwang,H.J.;Kang,J.W.Physica E 2005,27,163.doi:10.1016/j.physe.2004.11.004

(6) Hwang,H.J.;Choi,W.Y.;Kang,J.W.Comput.Mater.Sci.2005,33,317.doi:10.1016/j.commatsci.2004.12.068

(7) Zhang,Y.F.;Huang,H.C.Nanoscale Res.Lett.2009,4,34.doi:10.1007/s11671-008-9198-1

(8) Zhang,Y.F.;Huang,H.C.J.Appl.Phys.2010,108,10350710.

(9) Deng,C.;Sansoz,F.ACS Nano 2009,3,3001.doi:10.1021/nn900668p

(10) Deng,C.;Sansoz,F.Appl.Phys.Lett.2009,95,919149.

(11) Deng,C.;Sansoz,F.Nano Lett.2009,9,1517.doi:10.1021/nl803553b

(12) Yang,P.;Liao,N.B.;Yang,D.G.;Ernst,L.J.Microsyst.Technol.2006,12,1125.doi:10.1007/s00542-006-0235-7

(13) Yang,P.;Zhang,H.Z.Tribol.Int.2008,41,535.doi:10.1016/j.triboint.2007.10.011

(14)Liu,Y.H.;Gao,Y.J.;Wang,F.Y.;Zhu,T.M.;Zhao,J.W.Acta Phys.-Chim.Sin.2011,27,1341.[刘云红,高亚军,王奋英,朱铁民,赵健伟.物理化学学报,2011,27,1341.]doi:10.3866/PKU.WHXB20110605

(15) Wang,F.Y.;Gao,Y.J.;Zhu,T.M.;Zhao,J.W.Nanoscale Res.Lett.2011,6,291.doi:10.1186/1556-276X-6-291

(16)Gao,Y.J.;Wang,H.B.;Zhao,J.W.;Sun,C.Q.;Wang,F.Y.Comput.Mater.Sci.2011,50,3032.doi:10.1016/j.commatsci.2011.05.023

(17) Liu,Y.H.;Wang,F.Y.;Zhao,J.W.;Jiang,L.Y.;Kiguchi,M.;Murakoshi,K.Phys.Chem.Chem.Phys.2009,11,6514.doi:10.1039/b902795e

(18)Wang,F.Y.;Sun,W.;Gao,Y.J.;Liu,Y.H.;Zhao,J.W.;Sun,C.Q.Comput.Mater.Sci.2013,67,182.doi:10.1016/j.commatsci.2012.07.048

(19) Wang,F.Y.;Gao,Y.J.;Zhu,T.M.;Zhao,J.W.Nanoscale 2011,3,1624.doi:10.1039/c0nr00797h

(20) Verlet,L.Phys.Rev.1967,159,98.doi:10.1103/PhysRev.159.98

(21) Haile,J.M.;Gupta,S.J.Chem.Phys.1983,79,3067.doi:10.1063/1.446137

(22) Nose,S.Mol.Phys.1984,52,255.doi:10.1080/00268978400101201

(23) Hoover,W.G.Phys.Rev.A 1985,31,1695.doi:10.1103/PhysRevA.31.1695

(24) Johnson,R.A.Phys.Rev.B 1988,37,3924.doi:10.1103/PhysRevB.37.3924

(25) Johnson,R.A.Phys.Rev.B 1988,37,6121.doi:10.1103/PhysRevB.37.6121

(26) Liu,Y.H.;Zhao,J.W.;Wang,F.Y.Phys.Rev.B 2009,80,11541711.