太阳能小屋的设计模型

张永红，冯淑娟

(渭南师范学院数学与信息科学学院，陕西渭南714000)

1 问题的提出

在设计太阳能小屋时，需在建筑物外表面(屋顶及外墙)铺设光伏电池，光伏电池组件所产生的直流电需要经过逆变器转换成220 V交流电才能供家庭使用，并将剩余电量输入电网．不同种类的光伏电池每峰瓦的价格差别很大，且每峰瓦的实际发电效率或发电量还受诸多因素的影响，如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等．因此，在太阳能小屋的设计中，研究光伏电池在小屋外表面的优化铺设是很重要的问题．

2012高教社杯全国大学生数学建模竞赛题目(B题)附件1～7［1］提供了相关信息．请参考附件提供的数据，对下列3个问题分别给出小屋外表面光伏电池的铺设方案，使小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小，并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0．5元/kWh计算)及投资的回收年限．

问题1:请根据山西省大同市的气象数据，仅考虑贴附安装方式，选定光伏电池组件，对小屋(见附件2［1］)的部分外表面进行铺设，并根据电池组件分组数量和容量，选配相应的逆变器的容量和数量．

问题2:电池板的朝向与倾角均会影响到光伏电池的工作效率，请选择架空方式安装光伏电池，重新考虑问题1．

问题3:根据附件7［1］给出的小屋建筑要求，请为大同市重新设计一个小屋，要求画出小屋的外形图，并对所设计小屋的外表面优化铺设光伏电池，给出铺设及分组连接方式，选配逆变器，计算相应结果．

在求解每个问题时，都要求配有图示，给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式(串、并联)示意图，也要给出电池组件分组阵列容量及选配逆变器规格列表．

在同一表面采用两种或两种以上类型的光伏电池组件时，同一型号的电池板可串联，而不同型号的电池板不可串联．在不同表面上，即使是相同型号的电池也不能进行串、并联连接．应注意分组连接方式及逆变器的选配．

2 问题分析

问题1:要求给出一个优化的模型，解决一个全年太阳能光伏发电总量尽可能大而单位发电量的费用尽可能小的问题．依据题目给出的条件，首先利用Excel、Matlab工具对附件4［1］中所给的山西省大同市的气象数据及小屋各表面的有效面积等进行分析处理．仅考虑贴附安装方式，选定光伏电池组件，对小屋(见附件2［1］)的部分外表面进行铺设，并根据电池组件分组数量和容量，选配相应的逆变器的容量和数量．进而需要分别给出小屋外表面光伏电池的铺设方案，使小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小，并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0．5元/kWh计算)及投资的回收年限．

问题2:在问题1的基础上，各个表面的光伏电池组件的选择和铺设不变的条件下，进一步考虑电池板的朝向与倾角对光伏电池的工作效率的影响，选择架空方式安装光伏电池．利用附件6［1］所给的角度函数建立总发电量与倾角的函数关系，进而求解其最值，并求解同问题1相同的问题．

问题3:通过对问题1、问题2两种方式结果进行对比，根据附件7［1］中的小屋尺寸，选择架空方式定光伏电池组件，对小屋(见附件7［1］)的部分外表面进行铺设，并根据电池组件分组数量和容量，选配相应的逆变器的容量和数量．只需要对问题2中建立的模型进行改进．就能求出小屋外表面光伏电池的铺设方案，使小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小，并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0．5元/kWh计算)及投资的回收年限．

3 模型假设

(1)假设表面总辐射量小于80 W/m2时，光伏电池组件无法启动发电．

(2)假设在计算太阳能小屋投资费用时，仅考虑电池组块和逆变器的费用．

(3)符号说明如表1．

表1 相关符号说明

4 模型建立与求解

4．1 问题1

4．1．1 模型1:贴附安装下发电量最大优化模型

为简化计算，在此可通过电池表面太阳光辐照阈值(光伏电池组件启动发电时其表面所应接受到的最低辐射量限值，单晶硅和多晶硅电池启动发电的表面总辐射量超过80W/m2、薄膜电池表面总辐射量≥30 W/m2)进行判断，因此可建立如下整数规划模型:

相应地代入5个面上各个已知量的数据，用lingo编程求解出西立面、东立面、南立面、北立面上具体安排的组件个数的最优分布及最大发电量:

西立面:光伏电池选择x3=21，x20=1，最大发电量z1=3989500 W;

东立面:光伏电池选择 x2=1，x3=16，x4=1，x20=2，最大发电量 z2=2309282 W;

南立面:光伏电池选择x1=2，x2=1，x3=21，最大发电量z3=5810293 W;

北立面:光伏电池选择x1=11，x2=1，x3=21，最大发电量z4=1016506 W;

屋 顶:光伏电池选择x1=21，x2=2，x3=21，x4=2，最大发电量z5=2085471 W;

4．1．2 模型2:费用最小模型

根据太阳能小屋各个面上光伏电池的选择，设计出每个面上铺设光伏电池的具体排布及选择逆变器的数量、光伏电池的连接，此时考虑费用最小．

根据山西省大同市的气象数据［1］，得到表2．

表2 经济收益表

通过所有光伏组件在0～10年效率按100%计算，10～25年按照90%折算，25年后按80%折算出小屋的光伏电池35年寿命期内的总发电量为:

根据不同类型电池价格不同，通过对小屋西立面、东立面、南立面、北立面、顶面35年发电总量和民用电价算出小屋光伏电池在整个寿命期内产生的价值:经济效益862342060．64元．

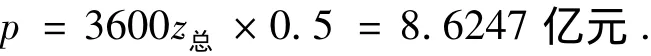
4．2 问题2

4．2．1 模型 3

电池板的朝向与倾角均会影响到光伏电池的工作效率，选择架空方式安装光伏电池，重新考虑问题1．确定输出量最大的情况下建立关于角度函数的公式建立方程模型:用Matlab对方程很容易求解出角度的最优值．然后用问题1的结果和角度之间的关系，问题可以简化为只考虑顶面的光辐射量．由光电板不同倾斜面上辐射量的计算公式［2］为:

其中:HT为太阳辐射至电池板，电池板所接收的太阳能;H，Hd为水平面的总辐射量和散射量;α为光电板倾角;ρ为地物表面的反射率，在工程计算中ρ一般取0．2，有雪覆盖的地面取0．7;Rb为倾角面与水平面的直射之比:

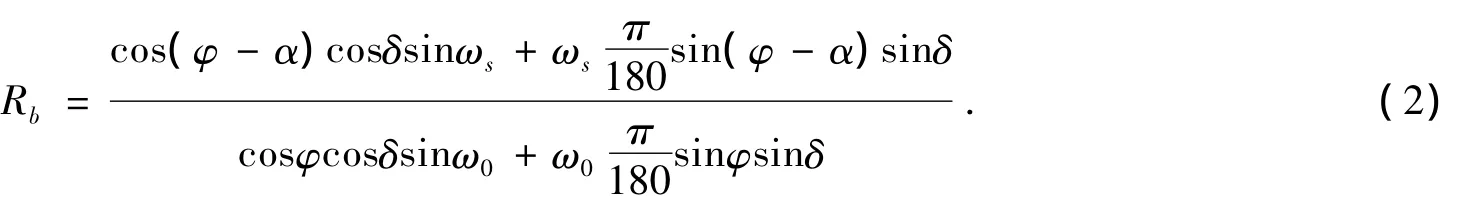
其中:φ为当地纬度;ωs，ω0是倾斜面和水平面的日落时角;δ为太阳赤角［3］．

n为日期序号．例如，1月1日为n=1，3月22日为 n=81．［4］

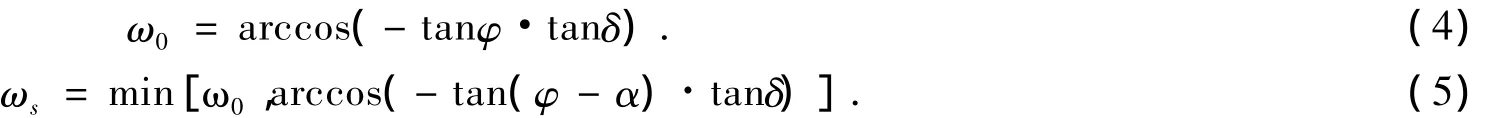
由以上各式可以建立HT关于α的函数关系式，通过微分思想，找到HT关于α的稳定点:

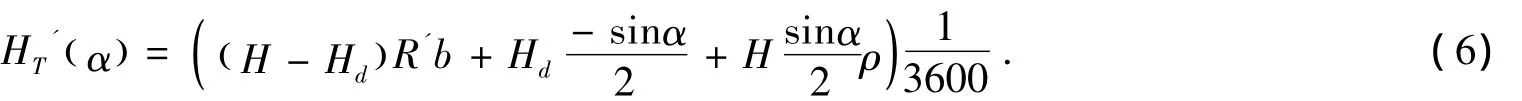
通过Matlab计算得到其稳定点程序，令HT

'(α)=0解得当°时，HT取得最大值．此时，max H(T)(α)=3．6606e+008 w ．

假设其他几个面光照辐射不发生变化，只考虑顶面的光照辐射．建立一年内在架空方式安装下电池主件发电量最优化模型(只对屋顶):

对于法向辐射强度IDN=I0Pm．

其中:I0表示垂直与大气层外边界出的太阳辐射强度;P表示大气透明度;m表示光线透过大气层的质量，忽略地球曲率的影响，大气质量

4．2．2 模型3的求解

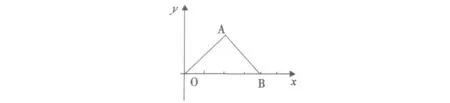
图1 倾斜面光照示意图

水平面直射太阳辐射强度［5］:IDH在Rt△OAB中，有IDN×AB=IPH×OH;则

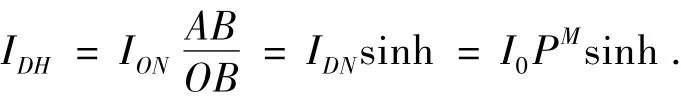
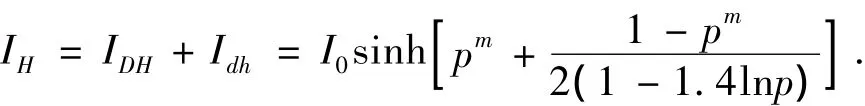
任意倾角面上的太阳辐射强度计算如下:

其中:IDH表示倾斜面上太阳直射辐射强度;Idh表示倾斜面上太阳散射强度;IRA表示斜面上获得地面反射辐射强度．

计算时角的计算公式为

其中:ts为太阳时(单位:小时)．

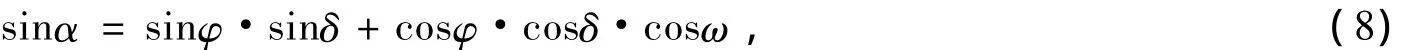
太阳高度角是太阳相对于地平线的高度角，这是以太阳视盘面的几何中心和理想地平线所夹的角度．太阳高度角可以使用下面的算式，经由计算得到很好的近似值:其中:α为太阳高度角，ω为时角，δ为当时的太阳赤纬，φ为当地的纬度(大同的纬度为40．1°)．太阳方位角(A)是太阳在方位上的角度，它通常被定义为从北方沿着地平线顺时针量度的角．它可以利用下面的公式，经由计算得到良好的近似值．

下面的两个公式也可以用来计算近似的太阳方位角，不过因为公式使用余弦函数，所以方位角永远是正值，因此，角度永远被解释为小于180°，而必须依据时角来修正．当时角为负值时 (上午)，方位角小于180°;时角为正值时 (下午)，方位角应该大于180°，即要取补角的值．

其中:A为太阳的方位角，α为太阳高度角，ω为时角，δ为当时的太阳赤纬，φ为当地的地理纬度．则在约束条件下解得最优解:kA1=21，kA2=2，kA3=21，kA4=2．其中:kAi表示 Ai的个数，i=1，2，3，4，进而计算可得最大发电量z=22342990 W．此时，小屋屋顶接受的太阳能用来转化电能，所需花费为电池组件花费+逆变器花费．电池组件花费为722．73×14．9=10768．677元;逆变器所花费用为35000×2+4500×2+22000+15300=116300元．

表3 电池组件及逆变器选择列表

4．3 问题3

利用附件7中给出的小屋建筑要求，建立关于小屋各个表面面积最大的最优化模型(模型4):

目标函数:Smax=log×wid+2×wid×hig+2log×hig－w log×wwid，

其中:log为长，hig为高，wid为宽，wwid为窗宽，w log为窗长．

运用 lingo 编程，可求出小屋的长、宽、高分别为:9．45 m、7．83 m、5．4 m;窗户的长、宽分别为:8．35 m、1．77 m．

从而可以得到各个表面的有效面积，进而可以利用模型3得到各个表面的铺设方案．又因为题目所给的条件小屋允许偏离正南朝向，因此对整个小屋进行旋转45°得到太阳能小屋的最优设计［5］．

5 模型的推广

光伏系统在整个寿命周期(目前为35年)内所产生的能量，远大于其制造、运输、安装、运行等阶段全部输入的能量，而且随着技术的进步，光伏系统的制造、安装过程中消耗的能量还将不断下降，能量偿还时间将进一步缩短，光伏发电确实是值得大力推广的绿色清洁能源．模型主要对太阳能小屋的发电量、经济效益进行了最优化研究，对今后在太阳能资源的利用方面提供了理论参考．

［1］湖南数学网络学院．2012高教社杯全国大学生数学建模竞赛题目［DB/OL］．(2012－09－07)［2012－11－25］．http://www．worlduc．com/e/blog．aspx?bid=10750389．

［2］吴建国．数学建模案例精编［M］．北京:中国水利水电出版社，2005．

［3］陈俊．光伏系统发电量计算的分析［J］．农村牧区机械化，2006，(2):27－28．

［4］杨金焕，毛家俊，陈中华．不同方位倾斜面上太阳辐射量及最佳倾角的计算［J］．上海交通大学学报，2002，36(7):1032－1036．

［5］杨卫国，夏红卫，魏生贤，等．竖直墙面不同方位上太阳辐射量的计算分析［J］．西南师范大学学报，2008，33(2):22－25．

［6］刘振宁，冯华，杨仁刚．山西不同地区太阳辐射量及最佳倾角分析［J］．山西农业大学学报(自然科学版)，2011，31(3):272－276．

［7］孙韵琳，杜晓荣，王小杨，等．固定式并网光伏阵列的辐射量计算与倾角优化［J］．太阳能学报，2009，30(12):1597－1601．