典型再入返回器气动特性对比与改进研究

詹慧玲 陈冰雁 刘周 周伟江

（中国航天空气动力技术研究院，北京 100074）

1 引言

返回器以第二宇宙速度返回地面时需要穿越高空、低雷诺数的非连续流区，然后进入高超声速、超声速、跨声速、亚声速的中低空连续流区，其间遇到的空气动力学问题很多，和第一宇宙速度载人再入飞行相比难度更大。因此返回器气动特性研究对宇宙飞船的研制起着先导和制约作用，并贯穿于飞船研制和发展的全过程[1]。

迄今为止成功实现载人空间再入飞行的航天器中，绝大部分采用的是轴对称的钝头体气动布局，如俄罗斯/前苏联的“东方号”、“上升号”和“联盟号”（Soyuz），美国的Mercury、Gemini和Apollo，以及我国的“神舟号”。目前美、俄正在研制的具备月球轨道返回能力的新一代载人航天器（美国的Orion和俄罗斯的PTK NP）的返回器外形仍采用轴对称钝头体布局，如图1所示[2-3]。

图1 美国的Orion（左）和俄罗斯的PTK NP（右）飞船返回器外形Fig.1 Reentry capsule configurations of American Orion and Russian PTK NP

美国的航天飞机是唯一采用非钝头体外形的载人航天器，但事实证明其发射和维护成本过高，目前已经退役。美国和俄罗斯对升力体布局的载人再入飞行器曾开展过研究（如X-38、Clipper），但也仅是针对近地轨道返回而设计的。对于登月或星际航行返回，再入地球大气层的速度远高于近地轨道的再入速度，采用升阻比较高的带翼飞行器或升力体外形设计的技术难度太大，目前的技术成熟度等级比较低。

Apollo 飞船返回器是唯一曾经成功地以第二宇宙速度再入的载人飞行器，对于探月或星际航行返回飞行器的气动设计而言，Apollo 的设计无疑是最具有参考价值的。事实上，美国正在研制的新一代星际航行飞船Orion 的载人探测飞行器（Crew Exploration Vehicle,CEV）外形设计就是在Apollo 的基础上进行的。因此，本文选择Apollo/CEV为主要参考对象，和Soyuz 飞船做对比分析。从两者气动特性的差别中得到外形的改进方向，提出了一种类Soyuz 改进设计的具体外形，并对该外形的升阻特性、稳定性以及配平特性进行了分析，可为新一代载人飞船返回器气动布局设计提供参考与借鉴。

2 典型返回器外形气动特性对比分析

Apollo[4]和CEV[5]均采用了球冠倒锥形布局设计，CEV 的倒锥角和球冠钝度（球冠半径Rn与最大横截面直径dm之比）基本沿用了Apollo 的设计参数，但最大截面直径尺寸大为增加（见表1）。俄罗斯的Soyuz 采用钟形设计，与Apollo和CEV 的倒锥形设计有较大的区别（如图2所示，为便于比较，图中外形尺寸以dm为参考长度进行了无量纲化；θ为倒锥角）。Soyuz 的倒锥角与Apollo和CEV 相比要小得多，球冠钝度也相对较小（见表1）。

为了了解类Soyuz 返回器气动特性和Apollo/CEV 这种返回器外形气动特性的主要区别，采用中国航天空气动力技术研究院自主研发的CFD 软件CACFD，对这3 种外形的气动性能进行了数值计算分析，重点对比分析这几个外形在高超声速下的气动特性。

表1 返回器外形参数Tab.1 Parameters of different reentry capsule configurations

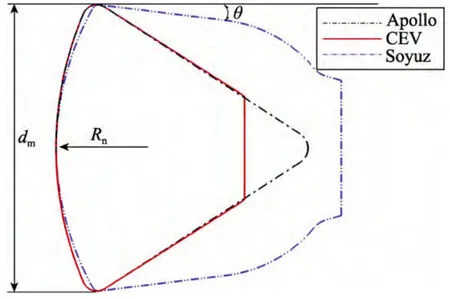
图2 返回器外形比较Fig.2 Comparison between different reentry capsule configurations

Apollo和CEV 外形相近，其气动特性也基本一致。图3为Apollo 与CEV 返回器在Ma=20 状态下的气动特性比较，图中，α为攻角；L/D为升阻比；CMzg为相对质心的俯仰力矩系数。为了得到正升力，球冠倒锥形返回器一般通过质心位置横偏的方法来实现负攻角配平，从而得到实现轨道机动控制所需的配平升阻比。所谓配平状态，是指绕质心的俯仰力矩为零的状态，配平状态下的攻角和升阻比称为配平攻角αT和配平升阻比L/DT。从图3 中2个外形的升阻比和俯仰力矩系数对比曲线可以看到，CEV 的升阻比随攻角变化曲线和Apollo 完全重合，配平攻角αT则略大，这主要与质心位置的设计有关。CEV 通过调整质心位置，增大偏心距离（以最大横截面直径dm无量纲化的横向质心系数Ycg从0.041 增大至0.048），使配平攻角（绝对值）从25.7°增大至28.7°，从而使配平升阻比L/DT从0.388 提高到0.432（见表2，表中Xcg为以最大横截面直径dm无量纲化的纵向质心系数），因为CEV 需要以更高的速度返回地球（从火星返回），对升阻比的要求更高。事实上，如果进一步增大配平攻角，CEV 的升阻比还能够进一步提高，在–45°攻角下，CEV 的升阻比可达0.65。但是由于受质心横偏量的限制，实际配平攻角和配平升阻比很难达到此值。

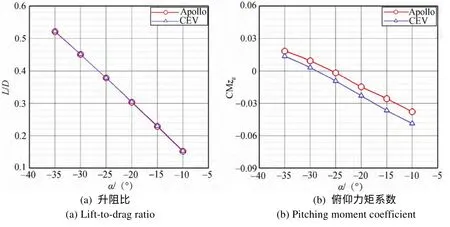
图3 Apollo 与CEV 返回器气动特性比较Fig.3 Comparison of aerodynamic characteristics between Apollo and CEV

从Soyuz和CEV 在Ma=20 下气动特性的对比曲线（见图4，图中CL为升力系数；CD为阻力系数）可以看到，Soyuz 的升力系数明显低于CEV，阻力系数在攻角绝对值大于30°以上明显高于CEV，因而升阻比显著低于CEV，并且随着攻角绝对值增加，差距越大。在–20°攻角，Soyuz 的升阻比为0.235，约为CEV 升阻比（0.305）的77%；而在–30°攻角，Soyuz 的升阻比为0.315，只有CEV 升阻比（0.451）的70%。

表2 Soyuz 与Apollo/CEV 气动性能参数比较（Ma=20）Tab.2 Comparison of aerodynamic parameters between Soyuz and Apollo/CEV (Ma=20)

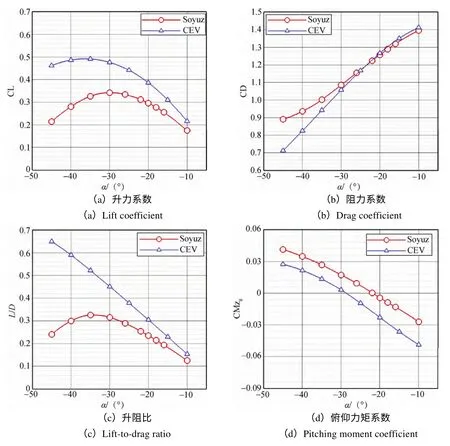
图4 Soyuz 与CEV 返回器气动特性比较Fig.4 Comparison of aerodynamic characteristics between Soyuz and CEV

Soyuz 的配平攻角在–22°左右，从表2 中可以看到，Soyuz 的配平升阻比和Apollo/CEV 相比要小很多，Soyuz、Apollo和CEV 的配平升阻比分别为0.225、0.388和0.441。即使通过增大配平攻角（分别增大到Apollo和CEV 的设计值：–25.7°和–29.3°），Soyuz 的升阻比可以提高至0.287和0.312，但是和Apollo/CEV 的数值相比还有不小的差距。而且通过增大配平攻角也很难进一步提高Soyuz 返回器外形的升阻比，Soyuz 外形的最大升阻比只有0.33，此时对应的攻角在–35°附近。

3 几何参数变化对返回器气动性能的影响

升阻比是衡量返回器气动性能的一个重要指标，较高的升阻比对于提高返回器的轨道机动能力，减小返回过程中的最大过载都是非常关键的。相关研究资料表明，为了扩大再入走廊、有效降低再入过载、增加纵向和横向调整能力、提高着陆点精度，登月飞船返回舱的升阻比应在0.3 以上[6]。

根据前面的分析，如果以Apollo 或CEV为参考的话，那么类Soyuz 外形的升阻比是偏小的。沿用类Soyuz 的外形设计是否能够实现类似Apollo 或CEV 的跳跃式返回轨道，并且能够满足载人返回的要求，这需要更为详细而深入的气动分析、轨道分析和飞行仿真计算。但是如果升阻比不够，完全可以通过对类Soyuz 外形几何参数的调整优化来提高其升阻比。

通过分别改变倒锥角θ和球冠半径Rn，同时保持其它关键外形参数不变，得出了这2个外形参数对类Soyuz 外形气动特性的影响规律。

3.1 倒锥角对返回器气动特性的影响

首先改变倒锥角θ，保持最大截面直径dm、球冠半径Rn以及底部外形不变，图5 给出了倒锥角从7°到16°变化下的返回器外形轮廓，随着倒锥角的增加，返回器的长度有所减小，相应的体积也有所减小。

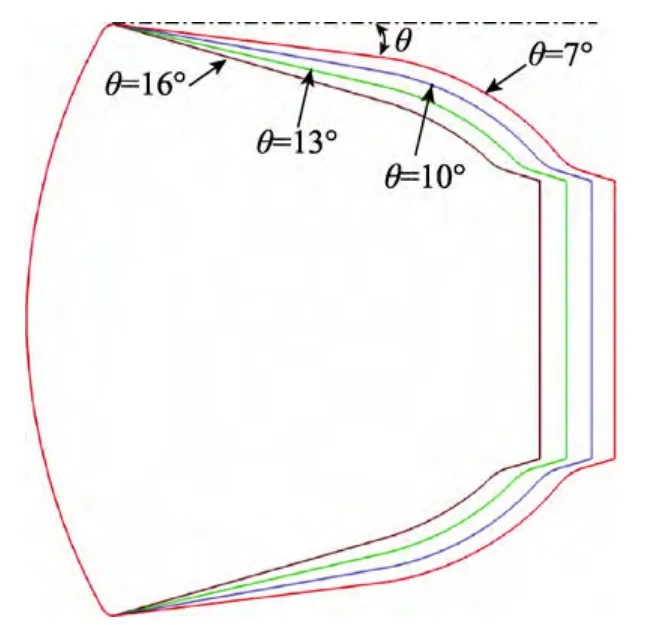
图5 不同倒锥角的返回器外形Fig.5 Reentry capsule configurations with different θ

3.1.1 θ 对升阻特性的影响

根据计算结果分析，增大倒锥角对于提高升阻比的效果比较显著。从表3 可以看到，在Ma=20，α=–20°的计算状态下，将倒锥角从Soyuz外形的设计值7°提高到16°之后，升阻比提高了15%，达到约0.27；并且随着攻角绝对值的增加，升阻比提高的效果更为显著，在α=–30°时，16°倒锥角外形的升阻比达到了0.384，比Soyuz 外形提高了将近22%。

表3 不同倒锥角下返回器外形的升阻比Tab.3 Lift-to-drag ratio of reentry capsule configurations with different θ

3.1.2 θ 对稳定性的影响

压力中心系数Xcp是反映返回器外形静稳定特性的一个重要参数（此处的Xcp为无量纲系数，参考长度为返回器最大截面直径dm）。一般而言，Xcp越大，表明压力中心位置越靠后，静稳定性越好。

表4 列出了在Ma=20，α=–20°状态下，4个不同倒锥角外形的压心系数计算值。可以看到，倒锥角增加到16°之后，返回器外形的Xcp比7°倒锥角时增加了约0.07，这意味着与Soyuz 返回器外形相比，压力中心位置后移了相当于最大截面直径（dm）7%的位移。

3.1.3 θ 对配平特性的影响

表5 列出了不同倒锥角外形的配平攻角和相对应的配平升阻比。在质心位置不变的前提下，倒锥角对返回器配平特性的影响规律是：αT的绝对值随θ 的增大而增大，相对应的L/DT也随θ 的增大而增大。但倒锥角对配平攻角的影响量并不大，θ=7°与θ=16°的配平攻角相差约1°。

表4 不同倒锥角下返回器外形的压心系数Tab.4 Center of pressure coefficient of reentry capsule configurations with different θ

3.2 球冠半径对返回器气动特性的影响

保持最大截面直径dm、倒锥角θ 以及底部外形不变，改变球冠半径Rn，得到不同球冠钝度的外形，如图6所示。图中所示外形的倒锥角θ=16°，球冠半径分别为2.5m和3.5m，相对应的球冠钝度分别为1.0和1.4。

图6 不同球冠半径的返回器外形Fig.6 Reentry capsule configuretions with different Rn

3.2.1 Rn对升阻特性的影响

球冠半径大小对返回器升阻特性的影响也是很显著的，根据计算结果分析，增大球冠半径也能够提高返回器外形的升阻比。从表6 可以看到，在Ma=20，α=–20°的计算状态下，将球冠半径从2.5m 提高到3.5m 之后，升阻比提高了约10%，达到约0.295 5；和倒锥角对升阻比的影响规律一样，随着攻角绝对值的增加，增大球冠半径对升阻比提高的效果也更为显著，在α=–30°时，3.5m 球冠半径外形的升阻比达到了0.433 1，比球冠半径为2.5m的外形提高了将近13%。

表6 不同球冠半径返回器外形的升阻比Tab.6 Lift-to-drag ratio of reentry capsules with different Rn

3.2.2 Rn对稳定性的影响

表7 列出了在Ma=20，α=–20°状态下，不同球冠半径外形的压心系数计算值。可以看到，球冠半径从2.5m 增加到3.5m 之后，返回器外形的压力中心位置后移了相当于最大截面直径dm2.2%的位移。

表7 不同球冠半径返回器外形的压心系数Tab.7 Center of pressure coefficient of reentry capsules with different Rn

3.2.3 Rn对配平特性的影响

在质心位置不变的前提下，球冠半径变化对返回器配平特性的影响和倒锥角的影响相比要更为显著（见表8）：球冠半径从2.5m 增加到3.5m 之后，αT从–23.1°变化至–29.3°，绝对值增加了6.2°，而倒锥角θ=7°与θ=16°的配平攻角相差不到1°；相对应的L/DT也从0.307 增大到0.424，增加了约38%。

表8 不同球冠半径返回器外形的配平参数（Ma=20）Tab.8 Trim parameters of reentry capsules with different Rn(Ma=20)

4 改进外形返回器气动特性分析

从以上分析可知，增大倒锥角θ和球冠半径Rn均可提高返回器气动外形的升阻比，并且还能在一定程度上提高配平状态附近的静稳定裕度，但是倒锥角和球冠半径也不是越大越好。在最大截面直径相等的情况下，倒锥角增大会使得容积利用率降低，球冠半径增大会使得拐角最大热流增大。因此，返回器的气动布局优化需要综合考虑各种影响因素。

本文对返回器外形设计的初步考虑是以提高类Soyuz 返回器外形的升阻比为主要目标，因此选择升阻比最高的外形（Rn=3.5m，θ=16°）为初步改进外形，标记为Soyuz-M，将改进外形的气动性能与Soyuz 原始外形以及CEV 返回器外形进行了对比分析。图7 给出了Soyuz-M 外形、Soyuz 外形和CEV 外形的比较（为便于比较，图中外形尺寸以dm为参考长度进行了无量纲化）。Soyuz-M 的倒锥角介于Soyuz和CEV 之间，球冠钝度Soyuz-M 是最大的。

图7 Soyuz-M/Soyuz/CEV 外形比较Fig.7 Comparison of configurations between Soyuz-M/Soyuz/CEV

4.1 升阻特性

类Soyuz 改进外形的升阻比和原始外形相比有了大幅度的提高，已经比较接近CEV 的升阻比。在Ma=20，α=–20°状态下，Soyuz-M 的升阻比为0.295 5，和Soyuz 的升阻比相比提高了26%，仅比CEV的升阻比低3%；在α=–30°时，Soyuz-M 的升阻比达到了0.433 1（见表9）。

表9 改进外形升阻比与Soyuz/CEV 的比较Tab.9 Comparison of lift-to-drag ratio between Soyuz-M and Soyuz/CEV

从Soyuz、Soyuz-M 以及CEV 这3个外形的升阻比随攻角的变化曲线比较（见图8）可以看到，Soyuz-M的升阻比随攻角的线性增长段和Soyuz 相比大为延长，在–35°攻角以内随攻角大小的增加基本是线性的，Soyuz 的升阻比在–35°已达最大值，而Soyuz-M 随攻角的进一步增大还有上升的趋势，这一特性与CEV比较一致。从升阻比随马赫数的变化曲线比较还可以看到，在Ma<5 时，3个外形的变化规律是不一样的，CEV 的升阻比随马赫数的降低而增大；而Soyuz-M 随马赫数的变化规律和Soyuz 是一致的，在Ma<5时，升阻比随马赫数的降低而减小。

图8 升阻比随攻角及马赫数变化曲线比较Fig.8 Lift-to-drag ratio vs angle of attack and Ma between Soyuz-M and Soyuz/CEV

4.2 稳定性

Soyuz-M 的压心系数介于Soyuz和CEV 之间（如图9所示），随攻角的变化规律都是一致的，即随攻角绝对值的增加而减小，也就是说，压心位置随攻角绝对值的增加而前移。在配平攻角附近，这3个外形的压心位置均比较靠后（见表10），比如在Ma=20、α=–20°时，Soyuz 的压心系数为0.638 1；Soyuz-M的压心位置和Soyuz 相比后移了将近最大截面直径dm的10%，为0.736 6；CEV 的压心位置更为靠后，压心系数为0.837 2。因此在配平攻角附近Soyuz-M、Soyuz和CEV 这3个外形的纵向静稳定裕度都很大，分别为35.3%、25.5%和57.2%。

图9 压心系数随攻角变化曲线比较Fig.9 Comparison of center of pressure coefficient vs angle of attack between Soyuz-M and Soyuz/CEV

表10 改进外形压心系数与Soyuz/CEV 的比较Tab.10 Comparison of center of pressure coefficient between Soyuz-M and Soyuz/CEV

由此可见，这3个外形在–20°攻角附近的静稳定性是非常好的，但是由于压心位置随攻角绝对值的增加呈前移的趋势，返回器外形的稳定性问题主要出现在攻角绝对值比较大的状态，比如Apollo 的压心系数最小值出现在α=–80°～–100°之间。因此，对改进外形静稳定性的分析还有待进一步的研究。

4.3 配平特性

通过绕质心的俯仰力矩系数随攻角变化曲线（如图10所示），可以得到配平攻角。在质心位置不变的情况下（Xcg=0.383 2，Ycg=0.033 6），Soyuz-M 的配平攻角绝对值与Soyuz 相比增加了7.3°，达到–29.3°，比CEV 的配平攻角–28.7°的绝对值还稍大（见表11）。

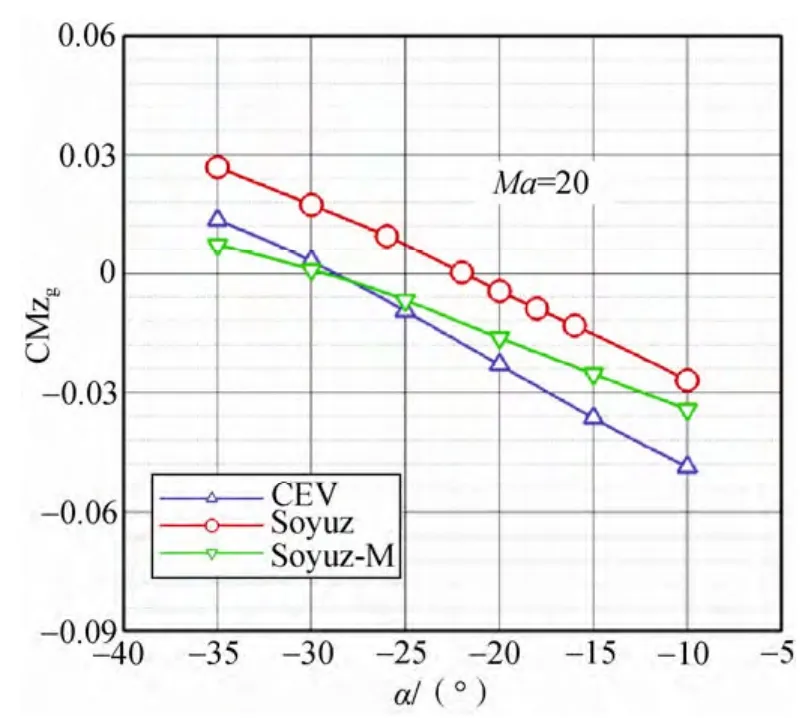
图10 俯仰力矩系数随攻角变化比较Fig.10 Comparison of pitching moment coefficient vs angle of attack between Soyuz-M and Soyuz/CEV

表11 改进外形配平参数与Soyuz/CEV 的比较Tab.11 Comparison of trim parameters between Soyuz-M and Soyuz/CEV

Soyuz-M 的配平升阻比达到了0.424，远远高于Soyuz 的配平升阻比0.255，和CEV 的配平升阻比0.432 已相差无几。而且Soyuz-M 的质心横偏量和Soyuz 是一样的，比CEV 的质心横偏量要小。增大质心横偏量还能够进一步增大配平攻角，提高升阻比。

5 结束语

文章对3 种典型飞船返回器外形（Apollo、CEV和类Soyuz）的气动特性进行了初步分析，与为第二宇宙速度返回而设计的返回器外形Apollo和CEV 相比，为第一宇宙速度返回而设计的类Soyuz 返回器外形的升阻比明显偏低。但是通过增大类Soyuz 返回器外形的倒锥角及球冠钝度，能够大幅提升返回器外形的升阻比。对调整后的返回器外形的初步分析表明，升阻比已比较接近Apollo和CEV，并且具有较好的静稳定性和配平特性。也就是说，在类Soyuz 飞船返回器的基础上对几何外形参数的调整优化来提高返回器外形的升阻比，从而满足第二宇宙速度再入返回的升阻比要求，这样的技术途径是可行的。当然，返回器的外形设计并不仅仅局限于满足升阻比的要求这么简单，还需要综合考虑动稳定性、轨道特性、热防护要求以及其它总体要求等因素。

References)

[1]赵梦熊.载人飞船返回舱空气动力学[M].北京:国防工业出版社,2000.ZHAO Mengxiong.Manned Spacecraft Re-entry Capsule Aerodynamics[M].Beijing:Defense Industry Press,2000.(in Chinese)

[2]http://www.russianspaceweb.com/ptk_np_2011.html,last accessed,20 Aug 2011.

[3]http://www.nasa.gov/mission_pages/constellation/orion/index.html,last accessed,20 Aug 2011.

[4]Hillje E R.Entry Aerodynamics at Lunar Return Conditions Obtained from the Flight of Apollo 4 (AS-501)[R].NASA TN D-5399,1969.

[5]Murphy K J,Bibb K L.Orion Crew Module Aerodynamic Testing[R].AIAA 2011-3502,2011.

[6]贾世锦.载人登月返回再入有关问题初步研究[J].航天返回与遥感,2011,32 (2):18-25.JIA Shijin.Preliminary Study on the Return and Re-entry of Manned Lunar Landing[J].Spacecraft Recovery &Remote Sensing,2011,32 (2):18-25.(in Chinese)

[7]闵学龙,潘腾,郭海林.再入参数调整对登月航天器返回再入特性的影响[J].航天返回与遥感,2010,31 (4):15-20.MIN Xuelong,PAN Teng,GUO Hailin.Reentry Parameters Change Influences on Manned Lunar Mission Capsule Reentry Characters[J].Spacecraft Recovery &Remote Sensing,2010,31 (4):15-20.(in Chinese)

[8]ZHAN Huiling,CHEN Bingyan,LIU Zhou,et al.Parametric Study on Aerodynamic Characteristics of Re-entry Capsules[C].Naples,Italy:63rd International Astronautical Congress,2012.

[9]CHEN Bingyan,ZHAN Huiling,ZHOU Weijiang,et al.Mechanism of Improving Aerodynamic Stability Characteristics of a Re-entry Capsule[C].Naples,Italy:63rd International Astronautical Congress,2012.

[10]陈冰雁,詹慧玲,周伟江，等.关于改善再入返回器稳定特性的气动设计研究[C].杭州：中国宇航学会深空探测技术专业委员会第九届学术年会论文集,2012:160-167.CHEN Bingyan,ZHAN Huiling,ZHOU Weijiang,et al.Study on Aerodynamic Design of Improving Stability Characteristics of a Reentry Capsule[C].CSA CDSET 9th Congress Proceedings,Hangzhou:Committee of Deep Space Exploration Technology of Chinese Society of Astronautics,2012,160-167.(in Chinese)

[11]耿云飞,李齐,赵会光.关于半弹道深空再入飞行器气动外形的讨论[C].杭州：中国宇航学会深空探测技术专业委员会第九届学术年会论文集,2012,154-159.GENG Yunfei,LI Qi,ZHAO Huiguang.Discussion on Aerodynamic Configuration of Semi-ballistic Reentry Vehicle[C].CSA CDSET 9th Congress Proceedings,Hangzhou:Committee of Deep Space Exploration Technology of Chinese Society of Astronautics,2012,154-159.(in Chinese)