轮形图K1∨Cn和扇形图K1∨Pn的解析

汪小黎，王 晓

(商洛学院 数学与计算科学系,陕西商洛 726000)

1引言及引用定理

本文所研究的图均为有限、无向、简单图。设G=(V(G),E(G))表示一个图，V(G)和 E(G)分别表示图G的顶点集和边集。图Pn表示n个顶点的路，图Cn表示n个顶点的圈，联图G1∨G2表示用G1中的每一个顶点连结G2中所有顶点且G1和G2各自的边保持不变所得到的图。联图K1∨Cn称为轮形图，联图K1∨Pn称为扇形图。其它涉及到的概念和定义可参见文献[1]。

Randic[2]在1979年提出图 G的解析（Dissection）的这一图的化学指标的概念，可以用来描述有机物的分子结构，和其他化学指标有着密切的联系[3-4]。它是一个关于图G的二元向量(a,b)，记图G的解析为 D(G)=(a(G),b(G))，在文献[3,5]中有如下递归定义：

1)若 G=K1，则 D(G)=(1,0)；

2)若 G=K2,则 D(G)=(1,0)；

由此递归定义，在文献[6]中，有如下关于图的解析的另一种计算方法。

设G为一个至少有三个顶点的连通图，V(G)={v1,v2,…,vn}，对于给定 v∈V(G)，在 V(G){v}中的顶点序列vi1vi2…vik若满足

1)在G-vi1-vi2-…-vik-1中包含v的连通分支至少有三个顶点；

2)在G-vi1-vi2-…-vik中v是孤立点；

3)对每个 j∈(2,3,…,k)，v 和 vij都在 G-vi1-vi2-…-vij-1的同一个连通分支中。则称序列vi1vi2…vik为相对于顶点v的一个链。图G中相对于v的链的数目记为a(G,v)。

对于给定边 e=vivj∈E(G)，在 V(G){vi,vj}中的顶点序列vi1vi2…vik满足

1)在G-vi1-vi2-…-vik-1中包含e的连通分支至少有三个顶点；

2)在G-vi1-vi2-…-vik中e是孤立边；

3)对每个 j∈(2,3,…,k)，e 和 vij都在 G-vi1-vi2-…-vij-1的同一个连通分支中。则称序列vi1vi2…vik为相对于边e的一个链。图G中相对于e的链的数目记为b(G,e)。

定理1[6]设G是一个至少有4个顶点的连通图，则有

在文献[5]中给出一些关于图的解析的基本性质，并给出一些常见图的解析值。

命题1[5]设n为一个正整数，则有

在文献[7]中给出树图的解析的上下界，图的解析的性质研究参见文献[5,8]。由其定义，可知道图的解析的计算是一个NP问题，本文结合图的解析两种计算方法，给出轮形图（图1）和扇形图（图2）的解析值。

2 主要结论

定理2设图G为轮形图K1∨Cn，n≥5,则有

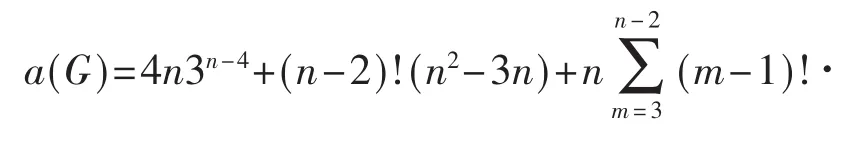
当 n=3，4 时，易计算得 D(K1∨C3)=D(K4)=(0,12)，D(K1∨C4)=(24,48)；D(K1∨P3)=(4,10)。

3定理的证明

3.1 定理2的证明

首先利用定理1来计算a(G)。如图1，轮形图G的中心点v0与圈中所有点都相连，所以去掉圈上的点，最后包含v0的子图要么是C3要么是P3（此时v0为中间顶点），所以相对于中心点v0的链的数目a(G,v0)。由对称性，圈上所有顶点的链的数目都相等。现取v为圈上一个顶点，设在关于顶点v的链中v0排在第m位，由于顶点v的每一个链必含有v0，故现对m进行分类来计算G中相对于v的链的数目。

1)m=1中心点v0在链的第一位，即首先去掉v0剩余是Cn。在Cn中相对于每个点的链数目是相等的，由命题 1，得所以m=1时，G中相对于v的链的数目为2×3n-4。

2)m=2中心点v0在链的第2位，即先去掉圈中除v外的一个顶点，再去掉中心点v0时，得到含v的一条路Pn-1。当链中第一个顶点取V(Cn){v}中不同点时，可得到顶点v位于长度为n-1的所有不同位置的路Pn-1由命题1，得中心点v0在第2位的链的数目为a(Pn-1)=2×3n-4。

3)3≤m≤n-2,中心点v0在链的第m位，即前面已去掉圈中的m-1个点。当这个m-1顶点的导出子图是一条路（也即这m-1个顶点在Cn中按一定次序依次相连）时，去掉中心点v0后，剩余的子图为包含v的路Pn-m+1。而且这相邻的

4)m=n-1中心点v0在链的第n-1位，即前面已去掉Cn中的n-2个顶点，剩余子图要么为含v和v0的C3要么是含v和v0的P3。当是C3时，由D(C3)=(0,3)，故这样的链的数目为0；当是P3时，与v0关联的另外一个顶点是在除了顶点v在圈上的两个临点外的顶点，故这样的链的数目为(n-2)!(n-3)。

5)m=n按这样的顶点序列顺序去掉顶点，最后剩余的子图为含v的一条边，故对a(G,v)的贡献为零。

对于b(G)，应用定理1，将轮形图G的边分为两类 E1和E2，其中 E1={vivo|i=1,2,…,n}，E2={vivj|vivj∈E(G),i,j=1,2,…,n}。若 e∈E1，则图G中相对于边e的链是由除去边e的两个端点，剩余n-1个顶点的任意排列，即b(G,e)=(n-1)!。若e∈E2，类似计算a(G)的分析，同理得到

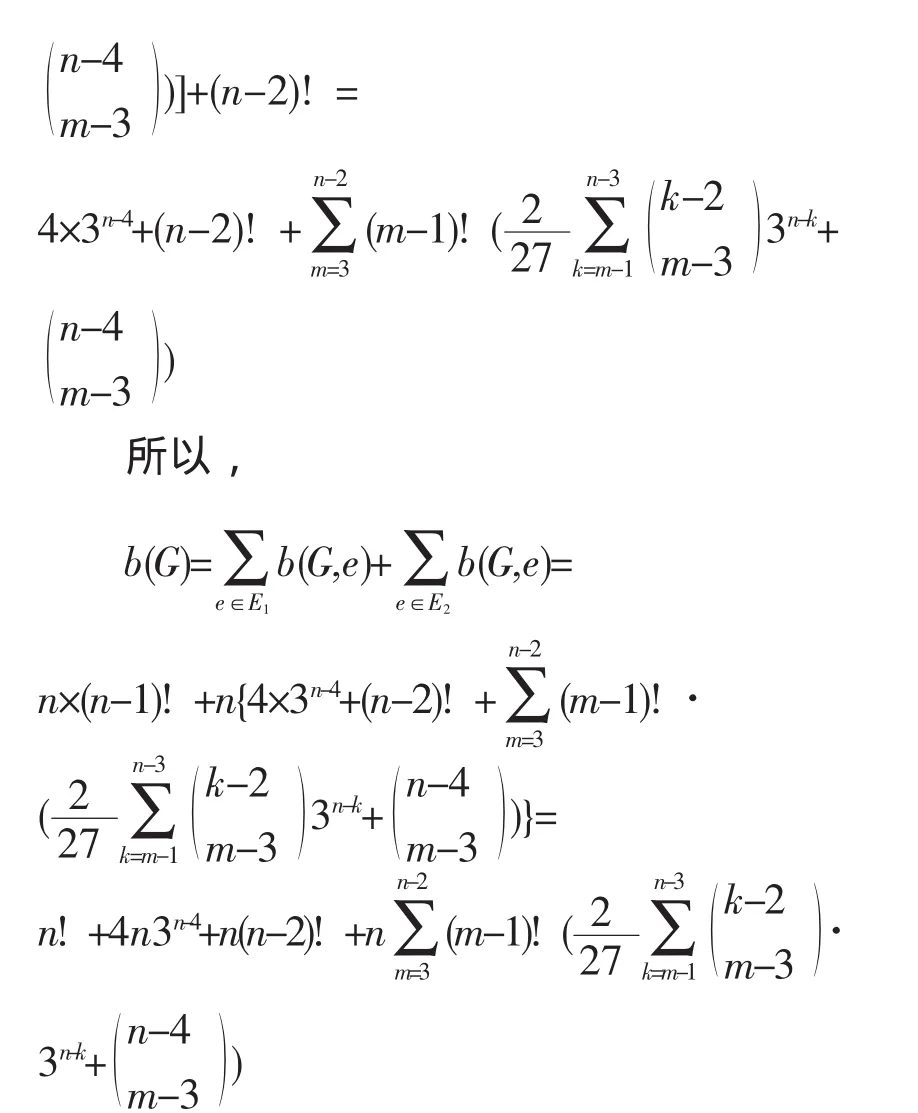
至此定理2得证。

3.2 定理3的证明

[1]BONDY J A,MURTY U S R.Graph theory with applications[M].Macmillan,London and Elsevier,New York,1976.

[2]RANDIC M.On dissection of acyclic graphs[J].MATCH Commun Math Comput Chem,1979,5:135-148.

[3]RANDIC M,GUO X F,CALKINS P.Graph dissetion revisited:application to smaller alikanes[J].Acta Chim Slov,2000,47:489-506.

[4]RANDIC M,WOODWORTH W L.Characterization of acyclic graphs by successive dissection[J].MATCH Commun Math Comput Chem,1982,13:291-313.

[5]XU Z X,WU B,GUO X F.On dissection of graphs[J].MATCH Commun Math Comput Chem,2006,56:519-526.

[6]段 芳,王 晓.A New method in computing the dissection of some graphs[J].新疆大学学报:自然科学版，2008，25(3)：293-297.

[7]王 晓,段 芳.On dissection of unicyclic graphs[J].华东师范大学学报,2009,1(143):13-21.

[8]张 莉.树的剖分值[J].应用数学学报,2008(31):852-860.