转子静偏心时异步电机径向力特性分析*
2013-09-15朱海峰祝长生
朱海峰,祝长生
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引 言
电机运行时,电机中存在基波磁场和一系列的谐波磁场,这些磁场相互作用,不仅会产生切向的电磁力矩,还会产生随时间和空间变化的径向力[1],电机正常运行的情况下,径向力的合力是很小的,但是当电机出现偏心时,会产生显著的低阶单边磁拉力。此时,不仅电机的振动和噪声会增大,严重时还会使电机的定、转子发生摩擦,缩短电机的使用寿命。电机电磁力计算一般采用近似解析法和数值分析法。近似解析法起源于上世纪40年代,该方法利用气隙磁导和磁势来计算气隙磁场产生的电磁力[2-3]。数值分析法是随着计算电磁学和计算机的发展而迅速发展起来的方法。由于这种方法能够考虑的因素较多,随着各种商用电磁场分析软件的普及应用和计算机性能的提高,目前电机电磁特性分析中大多数采用数值分析法来计算电磁力。吴正德等[4]运用有限元法计算出异步电机的传递函数,在通过传递函数计算电磁力,Ten⁃hunen等[5]讨论了在不同偏心率下,将异步电机的磁导视作线性的准确性,Pedro[6]和Dorrel[7]用有限元法计算了异步电机转子偏心时气隙磁场分布情况。
幅值较大的低阶径向力是引起电磁噪声的主要根源,当径向力的力波阶次及频率与电机某阶模态的阶次和频率相等时,发生谐振,电机的振动和噪声会显著增加[8]。因此为了研究降低电机的振动和噪声就必须同时弄清径向力波的频率、阶次和幅值,采用传统的解析算法可以准确地得到电磁力的阶次与频率,且计算快速,能够直观地反映电磁力与电机的结构和电磁参数间的关系;有限元算法能够考虑饱和、非线性等因素的影响,计算结果更加准确。
本研究采用近似解析算法和有限元法相结合,首先用近似解析法确定出异步电机在静偏心时径向力的主要频率和阶次,然后用有限元法校核径向力的频率和阶次,并定量地确定出径向力的大小。
1 理论分析
1.1 气隙磁场的建立
异步电机径向力的解析算法就是利用气隙磁导和磁势来计算气隙磁场产生的电磁力,当考虑齿槽和转子静偏心时,异步电机的定、转子建立的气隙磁场过程如图1所示[9]。当在定子三相对称绕组中通以三相对称电流时,定子绕组中的电流建立穿过气隙的磁压降(该磁压降包含基波分量和一系列由于定子绕组在空间上的非正弦分布导致的空间谐波分量),该磁压降与气隙磁导(包含常数项和由定、转子齿槽及偏心带来的谐波分量)相互作用,产生定子磁场部分。定子磁场在转子导条上感生电流,形成转子磁压降,转子磁压降与气隙磁导相互作用产生转子磁场部分,转子磁场同样会在定子绕组上感生出电流。通过这种相互作用形成了气隙磁场的各个组成部分。

图1 气隙磁场形成示意图
1.2 定、转子绕组磁势
定子绕组三相对称分布的异步电机运行时,定、转子绕组的合成磁势为:

式中:f0—基波磁势,fν—定子谐波磁势,fμ—转子谐波磁势,ν—定子谐波次数,μ—转子谐波次数。
电机在空载时可仅考虑其齿谐波的作用,因此定、转子谐波次数可写作:

式中:p—电机极对数;Z2—转子槽数;k1,k2—非零整数。
式(1)中,各磁势均为时间和空间的变量,具体表示为:
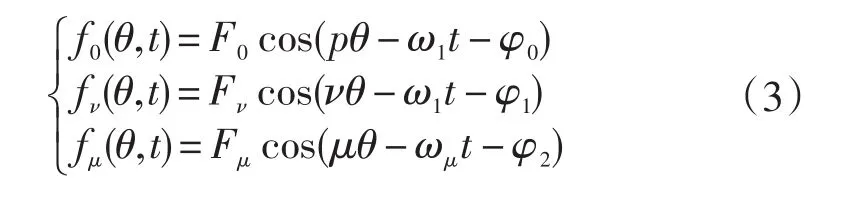
式中:F0—基波磁势幅值;Fν—定子谐波磁势幅值;Fμ—转子谐波磁势幅值;ω1—基波旋转角速度;ωμ—转子μ次谐波相对于定子的角速度;φ0,φ1,φ2—相位角。
1.3 静偏心时的气隙磁导
当转子不存在偏心时,考虑定、转子开槽带来的齿槽效应,气隙的磁导可近似表示为:

式中:第一项—为气隙磁导的不变部分,第二项—转子光滑而定子开槽引起的气隙谐波磁导,第三项—定子光滑而转子开槽引起的气隙谐波磁导,最后一项—定子和转子均开槽相互作用引起的气隙谐波磁导。
由于最后一项值较小,可以不考虑则不存在偏心时,考虑定、转子齿槽效应的气隙磁导为:

当转子与定子间出现静偏心时,会导致气隙分布的不均匀,此时气隙大小的表达式为:
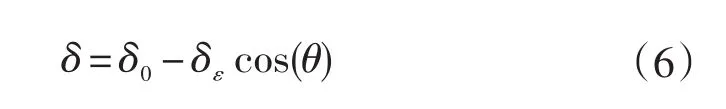
式中:δ0—均匀气隙,δε—静偏心值。
此时气隙的磁导为:

式中:ε—相对偏心率,ε=δε/δ0。
将式(7)进行傅里叶展开,在分解项中仅保留第一项,则得到转子静偏心时气隙磁导为:

1.4 转子静偏心时的气隙磁场及激振力
当转子静偏心时,气隙磁场为:
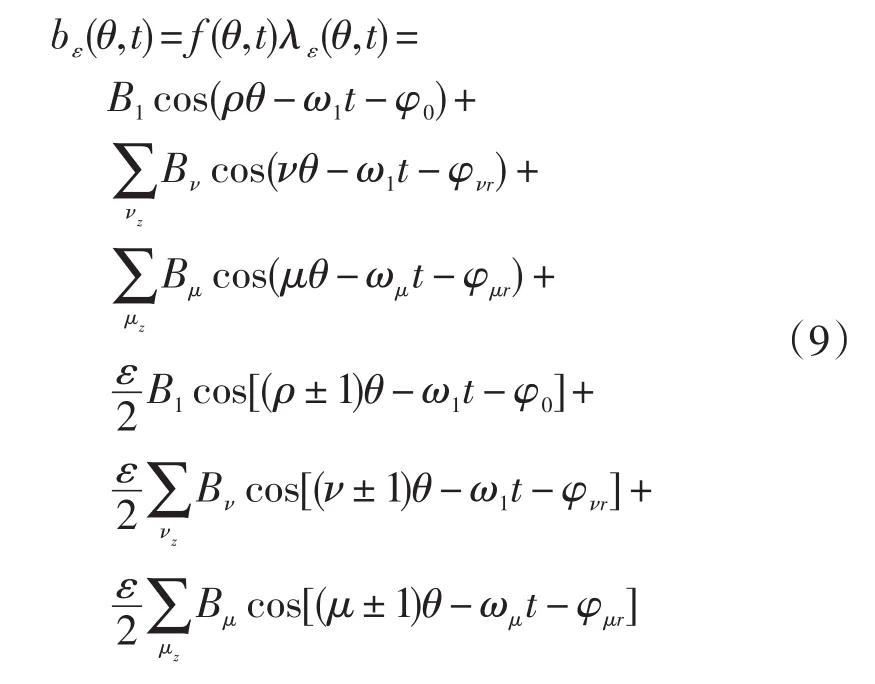
式中:前三项—异步电机正常运行时的气隙磁场,后三项—异步电机转子静偏心时所产生的附加磁场。
当异步电机出现转子静偏心时会在气隙中引起新的阶次而频率与正常运行时相同的附加磁场,且附加磁场的幅值正比于相对偏心率的一半。
由电机气隙产生并作用于定子铁芯内表面单位面积上径向电磁力的数值和分布,按麦克斯韦定律,正比于磁通密度的平方,可按下式确定:
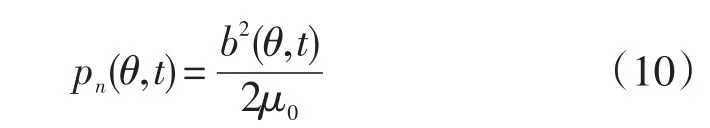
式中:μ0—空气的磁导率,由于振动阶数较低、幅值较大的力波对电机的振动和噪声起主要作用,而恒定分量不产生振动和噪声,因此本研究将式(9)代入式(10),并略去恒定分量以及振动阶数较高、幅值较小的力波分量,可得异步电机转子静偏心时径向电磁力的表达式为:

由式(11)可知,由转子静偏心所产生的p±1次附加磁场与基波磁场相互作用,可能产生一阶的低频径向力:

该力的频率为:

即当转子静偏心时,该力的频率可能为零。
2 有限元分析及计算
在用ANSYS进行异步电机的磁场分析后,各气隙单元的磁通密度为已知,本研究采用麦克斯韦应力张量法(Maxwell Stress Tensor),可以计算作用在电机定子内表面的切向力密度pt和径向力密度pn分别为[10]:
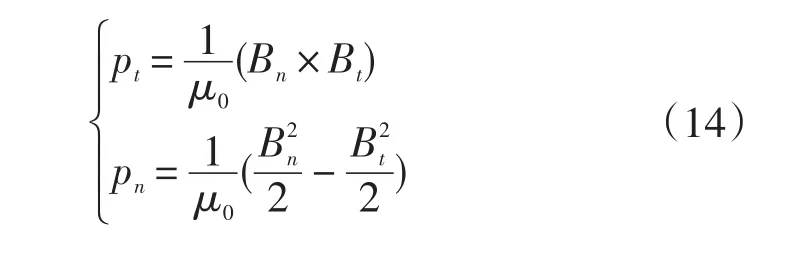
在进行异步电动机有限元电磁场分析时,研究者需对模型的边界条件进行假设,以简化计算。本研究所采用的基本假设为:①忽略异步电动机的端部效应,即电机沿轴向的磁场没有变化,将电机的三维电磁场简化为二维电磁场;②电机定子以外的空间不存在磁场;③电机材料为各向同性;④忽略位移电流;⑤定子通入三相对称交流电。
本研究仿真所用异步电机的主要结构参数为:电机极数2p=4,定子槽数Z1=36,转子槽数Z2=32。定子外径210 mm,定子内径136 mm,转子外径134 mm,转子内径48 mm,相对偏心率10%。
有限元计算的二维求解域及其网格划分如图2所示。
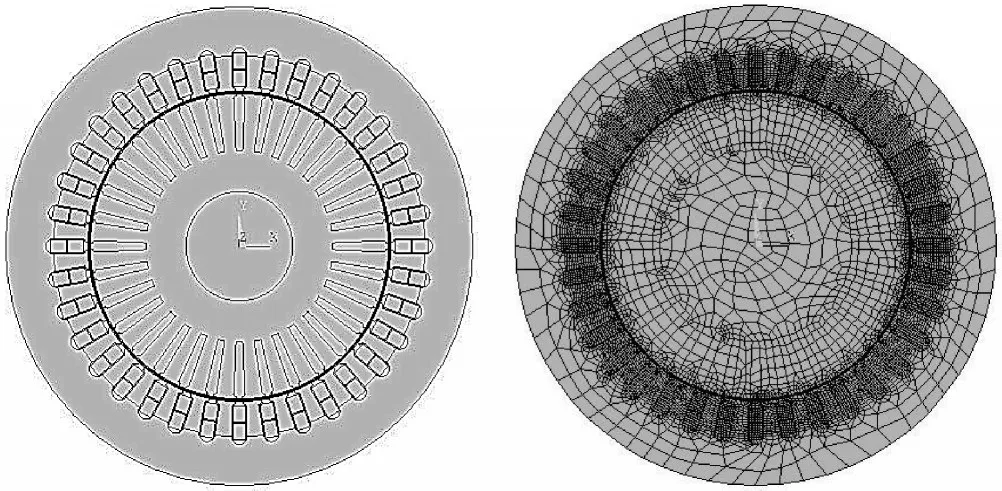
图2 异步电机二维求解域及其网格划分
为了考虑转子的旋转和沿周向均匀获取磁密值,笔者将气隙分为3个部分进行剖分,气隙剖分示意图如图3所示。内层气隙和外层气隙为自由剖分,内层气隙用于在添加转子旋转时予以删除和重建;中间气隙为固定剖分,沿周向分为720等份,以得到气隙中线上的磁密值。
本研究采用时步法计算,得到某时刻异步电动机没有静偏心和有静偏心的磁力线图4所示。
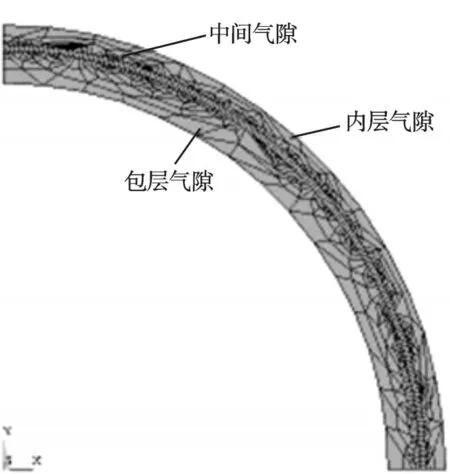
图3 气隙剖分示意图
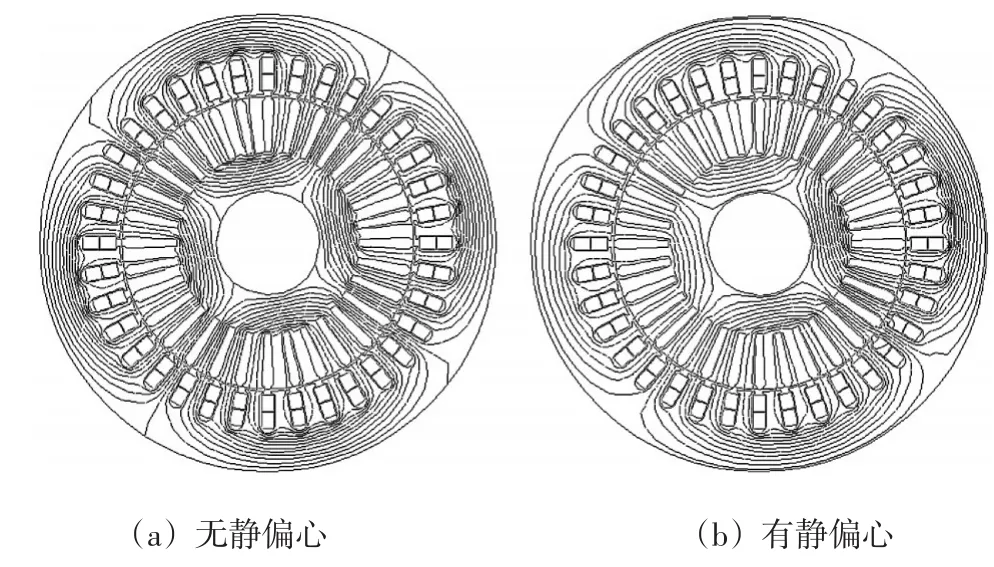
图4 电机磁力线分布
由图4比较可知,当电机不存在静偏心时,其磁力线的分布是对称的,而当静偏心存在时磁力线会向气隙小的那一端集中,磁力线分布更加密集。
根据式(6),电机转子在10%静偏心时气隙长度随空间角度的变化如图5所示。
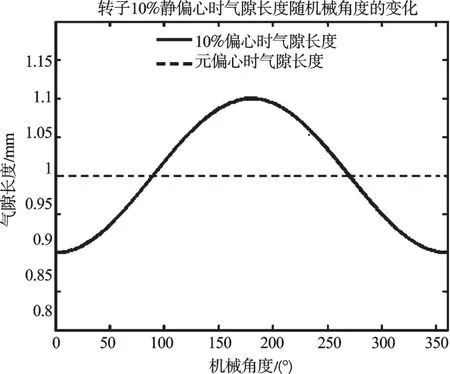
图5 电机气隙随空间角度的变化
从图5可以看出在(0,90)和(270,360)机械角度内出现静偏心的电机气隙小于正常运行时电机的气隙长度,在这些地方气隙磁导大于正常运行电机的磁导,同样的磁势产生的磁密也更大。正常运行及静偏心时气隙磁密如图6所示。

图6 正常运行及静偏心时气隙磁密
由麦克斯韦应力张量法计算异步电动机正常运行及转子静偏心运行时沿周向空间分布的径向电磁力和它们的频谱分析如图7所示。
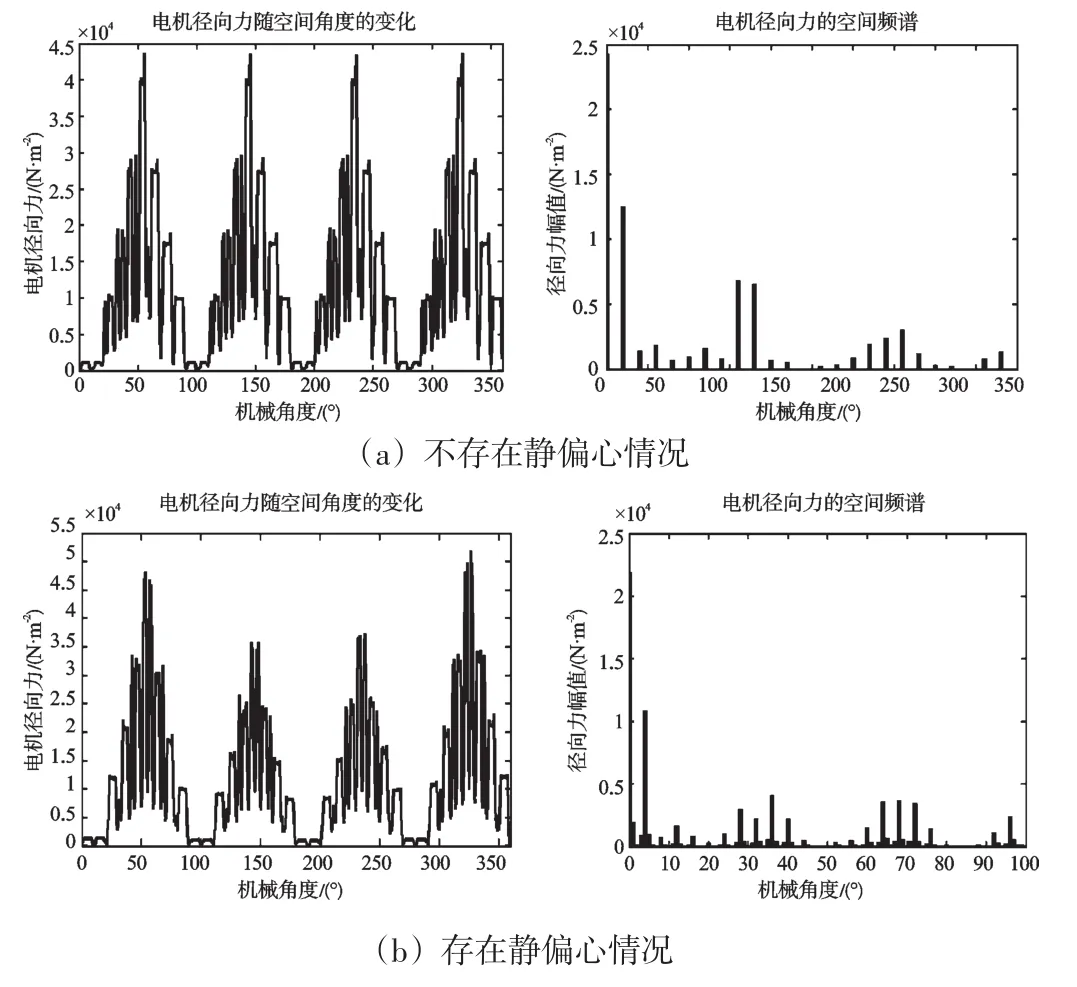
图7 径向力沿周向分布及其FFT
从电机在正常状态下运行和处于静偏心状态下运行的径向电磁力比较可知,在静偏心时在气隙较小处的径向电磁力明显大于气隙较大处的径向力,这将引起电机的单边磁拉力,且磁拉力的方向沿着使偏心增大的方向,从而进一步使电机的偏心程度增加,影响电机的性能,甚至导致电机出现转子与定子之间的碰磨故障。从静偏心时电磁力的空间频谱可以看出,除了电机正常运行时的力波阶次外,还额外产生了±1次的力波,主要的力波阶次如表2所示。

表2 主要径向电磁力的阶次分布
由理论分析可知,0阶力波为负一阶的定子齿谐波和正一阶的转子齿谐波磁场相互作用所产生;4阶力波包含两个分量:基波分量和正一阶的定子齿谐波和正一阶的转子齿谐波相互作用产生的力波;8阶力波由正一阶的定子齿谐波和负一阶的转子齿谐波相互作用产生;32阶力波为转子一阶齿谐波分量;36阶力波为定子一阶齿谐波分量。从图7可以看出,定、转子的齿谐波分量具有较大的幅值,但是由于其阶数较高,故而对电机的振动和噪声的影响并不大。
同样,采用麦克斯韦应力张量法计算气隙某一点径向电磁力随时间的变化如图8所示。
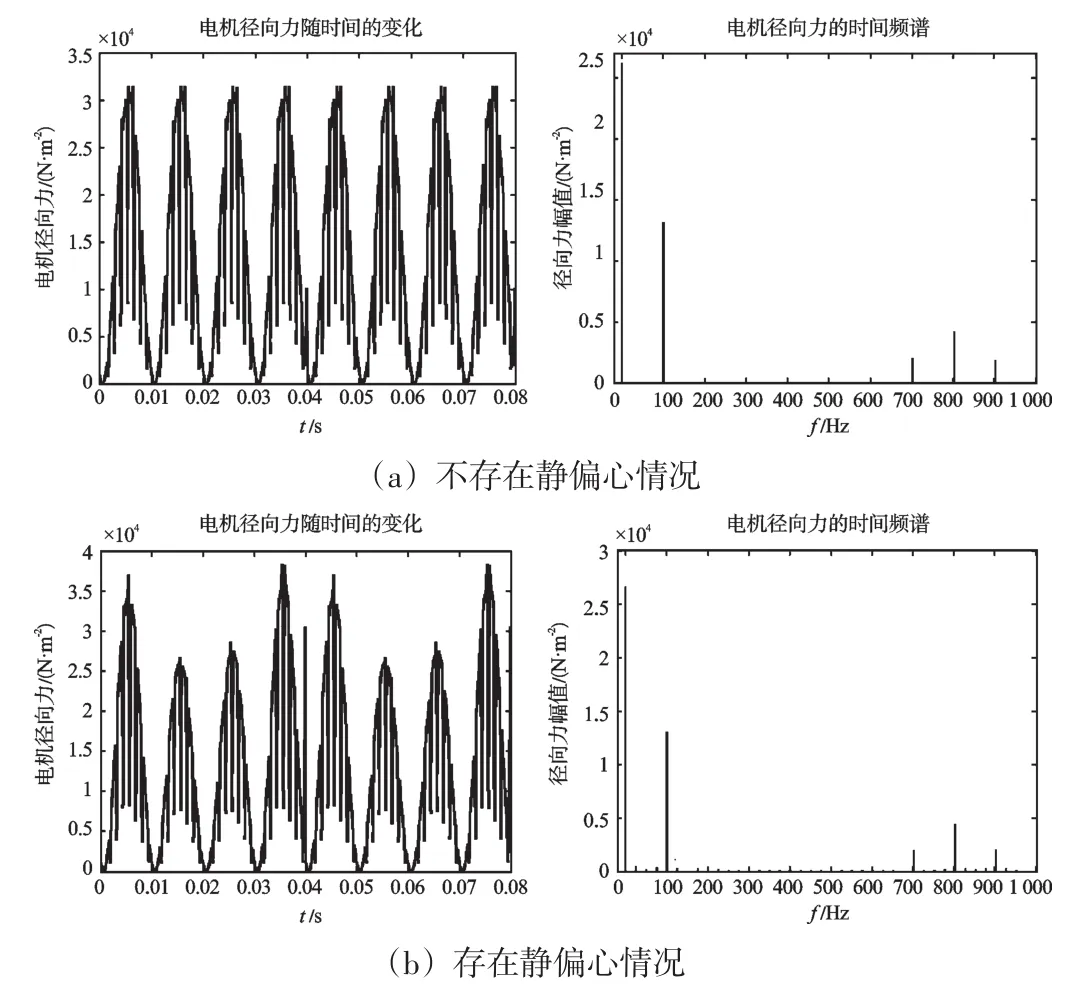
图8 径向力随时间变化及其FFT
从电机处于正常运行状态和静偏心运行状态某点径向力随时间的变化情况可以看出,正常运行时变化周期为一个电源时间周期(0.02 s),静偏心运行时变化周期为两个电源时间周期(0.04 s),这是由于在正常运行时每对极下的气隙分布情况相同,而静偏心时气隙以磁极中心线为对称轴对称分布,当忽略转差,两对极电机旋转一周需要两个电源时间周期。从它们的时间频谱可以看出,静偏心运行时电磁力并未产生新的频率,这与理论的推导是一致的。
3 径向电磁力的定量确定
通过以上分析可知,在异步电机的径向电磁力中同一频率但力波的阶次可能不同,力波的频率不同但阶次有可能相同。异步电机的振动和噪声既与径向力波的频率有关,也与其频率相关。为了更好地确定异步电机在不同结构和运行状态下产生的力波对电机振动和噪声的影响,同时确定出径向力的幅值、阶次和频率是十分必要的。为了达到这一目标,本研究首先由式(11)确定出对异步电机电磁振动和噪声影响较大的径向力的阶次和频率如表3所示。
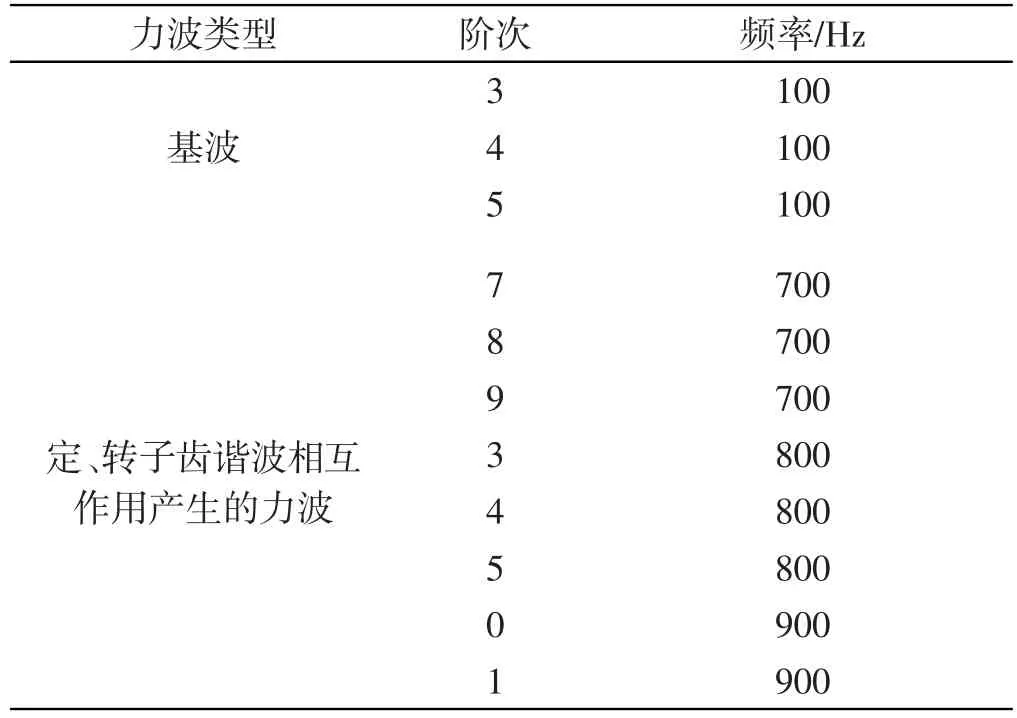
表3 静偏心时主要径向力的阶次和频率
在确定出异步电机径向力的阶次和频率之后,需要借助二维的傅里叶分解方法对径向电磁力的阶次和频率进行校核,并确定出径向力的幅值。径向电磁力波以空间角度φ和时间t为变量,其二维的傅里叶分解如下式所示:

式中:m,n—径向电磁力的空间阶次和时间频率。
为了对径向电磁力波进行二维傅里叶分解,就必须得到径向电磁力随时间和空间变化的二维矩阵,这通过ANSYS可以很容易地实现,然后用Matlab将得到的矩阵进行二维傅里叶分解,便可同时得到径向力波的幅值、频率及阶次。以异步电动机在静偏心稳态运行为例,可得二维傅里叶分解的结果如图9所示。
由图9可知直流分量和基波分量在异步电机的径向电磁力中占据主导作用,而直流分量对电机的振动和噪声无影响,基波分量的振动阶次低,可能会产生明显的振动和噪声。其他谐波分量虽然幅值较小,但有的基波分量阶次低且频率接近或者等于电机的固有频率,也可能对电机的振动和噪声产生明显的影响。

图9 电机径向力二维FFT
结合由理论公式计算出的对异步电机振动和噪声影响较大的电磁力波的阶次和频率以及由有限元计算出的电磁力波幅值,可以得到本研究所建电机在10%静偏心下运行的主要激振力如表4所示。

表4 电机在10%静偏心运行时的主要径向力情况
由式(11)可知,由静偏心引起的附加力波幅值应与偏心量成正比,与表4结果一致。
4 结束语
本研究运用理论分析和有限元计算相结合的方式计算异步电机静偏心时的径向力分布,首先通过理论分析得到主要的力波阶次和频率,然后通过有限元法校核并得到力波的幅值,得到的主要结论如下:
(1)异步电机静偏心时会在原有力波基础上产生新的阶次而频率相同的力波,其幅值正比于相对偏心率,新产生的力波阶次较低,可能对振动产生较大影响。
(2)偏心后产生的单边磁拉力会使偏心进一步加大,使电机运行情况恶化。
(3)通过理论计算可以得到对电机振动和噪声影响较大的力波的阶次和频率,而通过有限元计算后对力波进行二维的傅里叶分解,可以得到对用阶次和频率力波的幅值,两者的结合可以为减少电机的振动和噪声提供理论上的依据。
(References):
[1]周思刚.气隙不均匀对异步电动机电磁噪声的影响[J].研究与开发,2006(8):49-51.
[2]陈永校,诸自强,应善成.电机噪声的分析和控制[M].杭州:浙江大学出版社,1987.
[3]舒波夫.电动机的噪声和振动[M].沈官秋,译.北京:机械工业出版社,1980.
[4]WU D,PEKAREK S D,FAHIMI B.A field reconstruction technique for efficient modeling of the fields and forces within induction machines[J].IEEE Transactions on En⁃ergy Conversion,2009,24(2):366-374.
[5]TENHUNEN A,HOLOPAINEN T P,ARKKIO A.Spatial linearity of an unbalanced magnetic pull in induction mo⁃tors during eccentric rotor motion[J].The International Journal for Computation and Mathematics in Electri⁃cal and Electronic Engineer,2003,22(4):862-876.
[6]JOVER RODRIGUEZ P V,BELAHCEN A,ARKKIO A,et al.Air-gap force distribution and vibration pattern of Induc⁃tion motors under dynamic eccentricity[J].Electrical Eng⁃eering,2008(90):209-218.
[7]DORRELL D G,THOMSON W T,ROACH S.Analysis of airgap flux,current and vibration signals as a function of the combination of static and dynamic airgap eccentricity in 3-phase induction motors[J].IEEE Transaction on In⁃dustry Engineering,1997,33(1):563-570.
[8]TÍMÁR P L.Noise and Vibration of Electrical Machines[M].Amsterdam:Elsevier,1989.
[9]SAHRAOUI M,GHOGGAL A,ZOUZOU S E,et al.Dynam⁃ic eccentricity in squirrel cage induction motors-Simula⁃tion and analytical study of its spectral signatures on stator currents[J].Simulation Modelling Practice and Theory,2008(16):1503-1513.
[10]佟宁泽.大中型感应电机电磁力及定子振动分析[D].沈阳:沈阳工业大学电气工程学院,2006.
