关于肿瘤细胞破坏并入侵正常组织或细胞质基质的数学模型的分析*

张久远，冯兆永，刘成霞，卫雪梅

(1.广东工业大学应用数学学院，广东广州 510006;2.中山大学数学与计算科学学院，广东广州 510275;3.广东省口腔医院，广东广州 510280)

固体肿瘤的生长为分两个阶段:未血管化阶段和血管化阶段。在肿瘤生长初期，肿瘤没有形成自己的毛细血管。营养物质仅靠简单的扩散进入肿瘤，而肿瘤细胞获得营养物质比较有限，这使肿瘤生长的大小受到了较大的限制。肿瘤的这个阶段称为未血管化肿瘤。对人体的健康构成严重威胁的肿瘤是已经血管化的肿瘤。在这个阶段肿瘤寄生的正常组织中的毛细血管侵入肿瘤，使肿瘤形成自己的毛细血管系统，通过血液循环使肿瘤细胞在远处器官中建立新的领地，这个过程称为转移。这种从单一原发性肿瘤到全身不同部位的多发性肿瘤的发展过程是肿瘤恶性生长阶段，也是肿瘤难以治愈的主要原因之一。

本文研究一个肿瘤细胞入侵正常组织或细胞外基质的数学模型［1］。这是一个由蛋白水解酶活性肿瘤细胞引起的综合过程，例如尿激酶型纤溶酶原激活物 (uPA)和蛋白水解酶 (MMPs)破坏细胞外基质的蛋白。(uPA)自身引发酶激联反应，主要涉及纤维蛋白酶原的激活物及其随后的基质降解蛋白纤维蛋白溶酶的激活。基质的降解促使肿瘤细胞穿过组织迁移随后扩散到身体的其他部位，从而形成肿瘤的转移。该模型由描述肿瘤细胞，尿激酶，尿激酶抑制剂，纤溶酶和宿主组织之间的相互作用的四个含有交叉扩散的抛物方程和一个退化的抛物方程组成。模型具体表述如下:

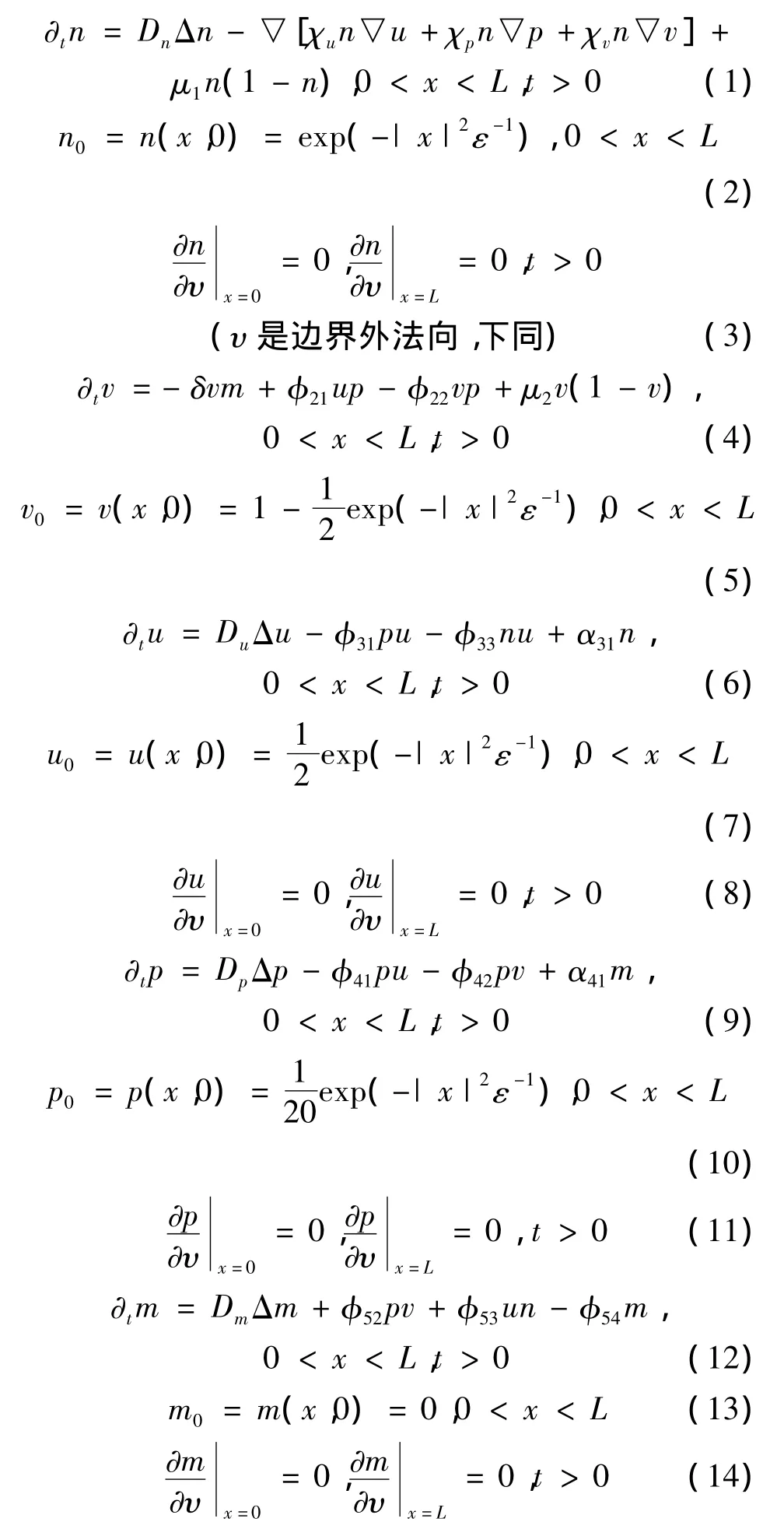
其中n(x，t)，v(x，t)，p(x，t)，u(x，t)，m(x，t)分别代表肿瘤细胞密度，细胞外基质蛋白玻连蛋白浓度，纤溶酶原激活物抑制剂的浓度，纤溶酶原激活物的浓度，纤维蛋白溶酶浓度［1］。Dn代表随机动能系数 ，μ1代表扩散率，χu代表尿激酶型纤溶酶原激活物介导的趋触性系数，χp代表纤溶酶原激活物抑制剂介导的趋触性系数，χv代表细胞外基质蛋白玻连蛋白浓度介导的趋触性系数;δ表示降解率，μ2代表扩散率，φ21表示产生的纤溶酶原激活物抑制剂或纤溶酶原激活物的结合速率，φ22表示纤溶酶原激活物抑制剂与细胞外基质蛋白玻连蛋白结合的制衡力;Du，α31，φ31和φ33，分别代表纤溶酶原激活物的扩散系数，由癌细胞引起的纤溶酶原激活物产生速率，纤溶酶原激活物抑制剂引起中和，及其与细胞表面受体结合速率;Dp，α41，φ41和φ42分别表示:纤溶酶原激活物抑制剂扩散系数，由纤维蛋白溶酶合成引起的纤溶酶原激活物抑制剂产生速率，由纤溶酶原激活物作用引起的纤溶酶原激活物抑制剂中和速率和由细胞外基质蛋白玻连蛋白结合作用引起的纤溶酶原激活物抑制剂中和速率;Dm，φ52，φ53，分别表示:纤维蛋白溶酶扩散系数，由纤溶酶原激活物/尿激酶型纤溶酶原激活物受体结合引起的纤维蛋白溶酶的生产速率，由纤溶酶原激活物抑制剂或细胞外基质蛋白玻连蛋白浓度引起的生产速率［2］，这些所有的参数均为大于零的正常数。

本文假设以下条件成立:

(A)对任意的0＜α＜1，n0(x)，v0(x)，u0(x)，p0(x)，m0(x)∈C2+α(¯Ω)。

定理1 在条件 (A)成立时，对任意t≥0，系统 (1)－(14)存在唯一的整体解。

1 基本引理

首先引进一些记号:

①记ΩT=［0，L］×(0，T)是它的闭包。

②对p＞，记Dp(0，1)为t=0 时(QT)的迹空间，i.e.φ∈Dp(0，1)当且仅当 ∃u∈(Q)，使得u(·，0)=φ 。定义D(0，1)中的Tp范数如下:

由于p＞时，(QT)连续嵌入到C(QT)(见文［3］)，上面的定义是有意义的。而且，显然如果φ ∈W2，p(0，1)，则 φ ∈Dp(0，1)且。

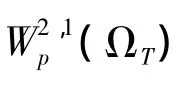
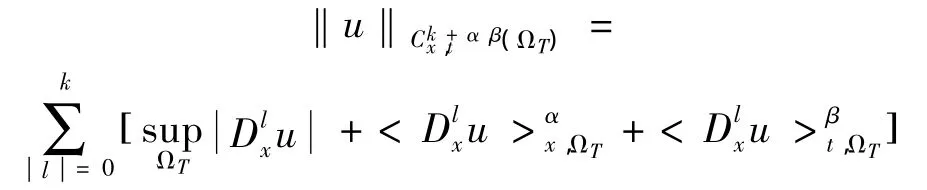
其中

下面介绍几个有用的引理。

引理1［4］假设D是一个正常数，a(x，t)，b(x，t)，是区间上连续有界的函数，f(x，t)∈Lp(ΩT)，φ ∈C1［0，T］，且对1＜p＜∞ ，u0(x)∈DP(0，L)。令Bu=α(∂u/∂n)+βu，其中 (1)α=0，β=1;(2)α=1，β≥0。则初值问题

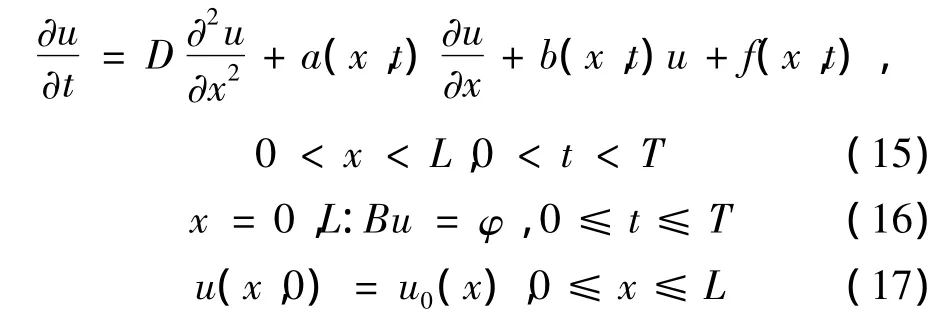
其中Cp(T)一个依赖于D，p，T，‖a‖∞，‖b‖∞的常数，且对任意的T有界集，Cp(T)是有界的。

引理 2［5－6］设a(x，t)，b(x，t)，f(x，t)∈Cα，α/2(ΩT)和u0(x)∈C2+α［0，L］，则初值问题(15)－(17)存在唯一解u(x，t)∈C2+α，1+α/2()，且

(i)当α=0，β=1时，有

(ii)当α=1，β=0时，有

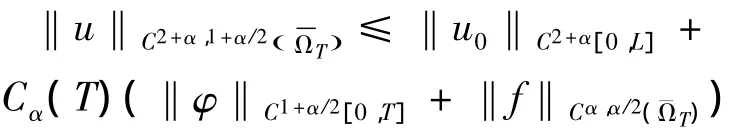
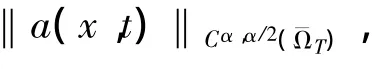
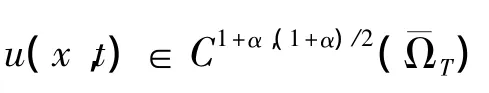
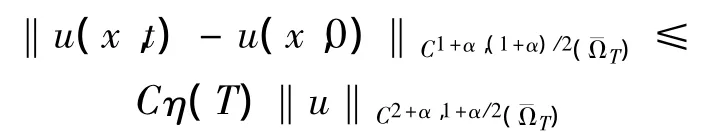
2 局部解的存在唯一性

本节证明问题 (1)－(14)存在唯一局部解。对任意给定的T＞0和一个正常数M，引入度量空间 (XM，d)。对任意n(x，t)，v(x，t)，u(x，t)，p(x，t)，m(x，t)(0＜x＜L，0＜t＜T)，满足如下条件:

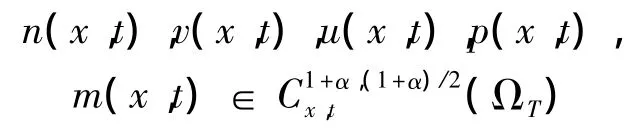
并满足问题 (1)－(14)且

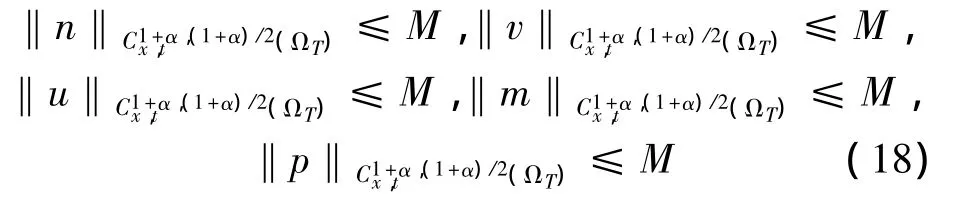
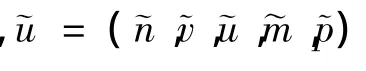
很显然(XM，d)是一个完备的度量空间。

对任意的u定义一个映射F:u→，其中满足如下问题:

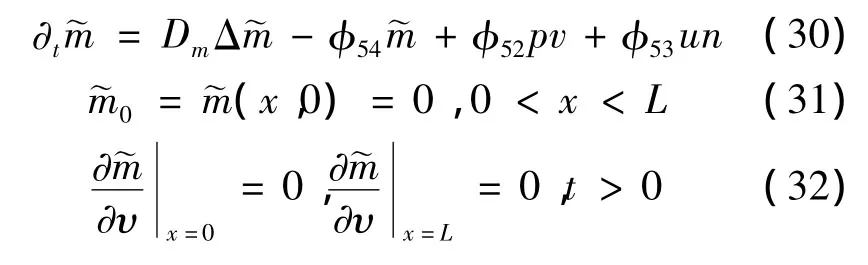
下面先证明F:映XM→XM。

(i)对问题 (22)－(23)显然有唯一解∈，且有

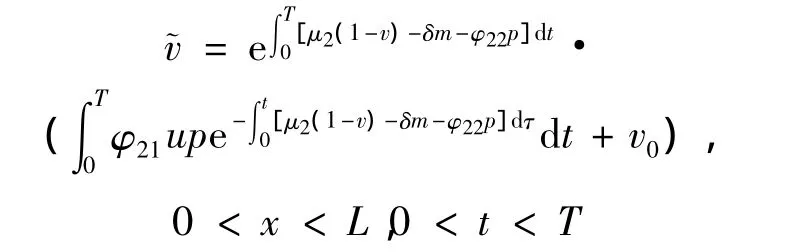
若M＞‖v0‖C1+α［0，L］+1 ，且T足够小时，则有

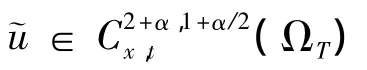
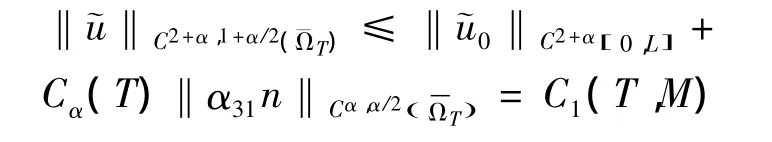
再由引理3可得

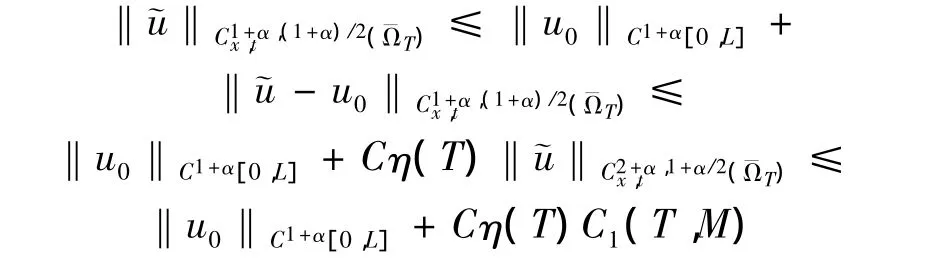
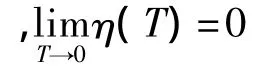
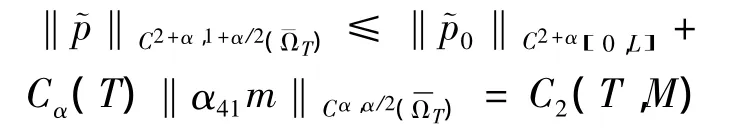
结合引理3可得

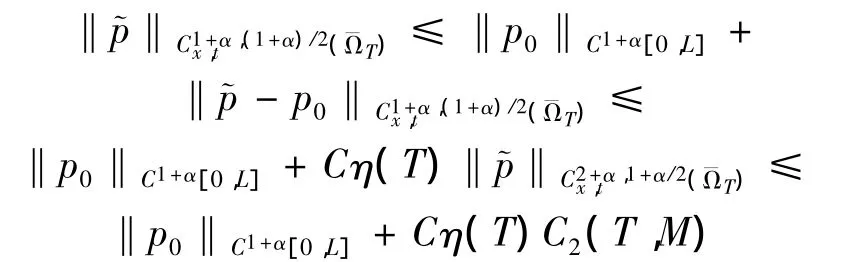
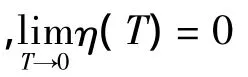
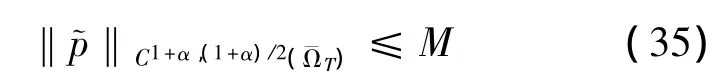
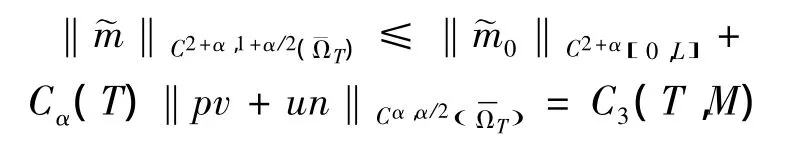
结合引理3可得

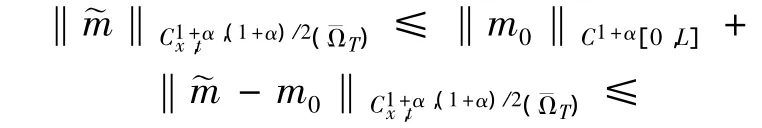
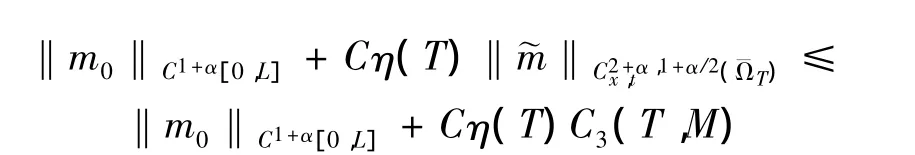
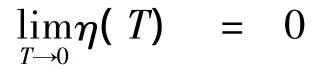
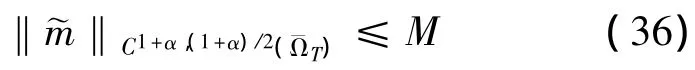
(v)考虑问题 (19)－(21)，为方便记

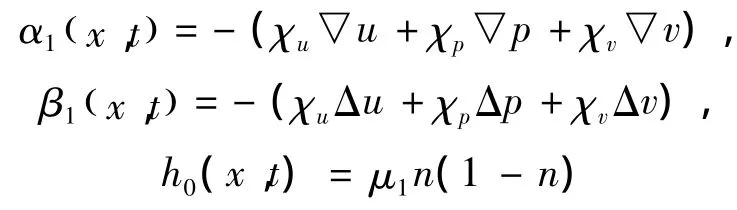
由 (i)－(iii)的结论可知

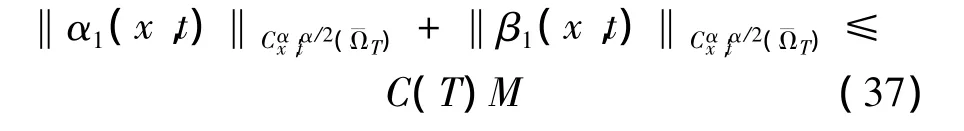
计算可知 (19)可化为下面的形式

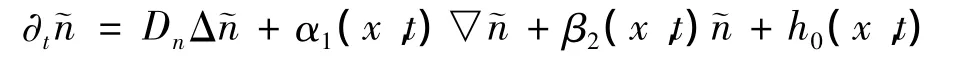
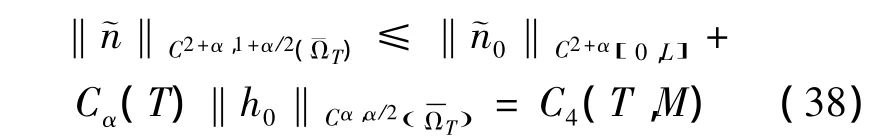
结合引理3

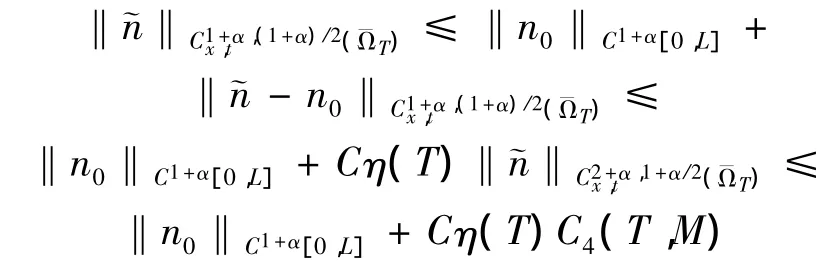
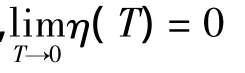
下面我们证明F是压缩的，对任意u1，u2∈XM，假设

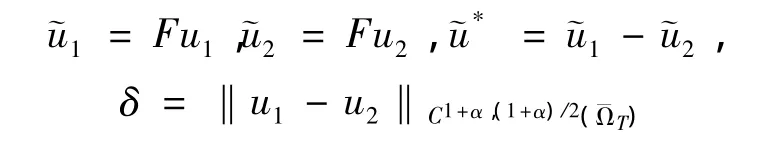
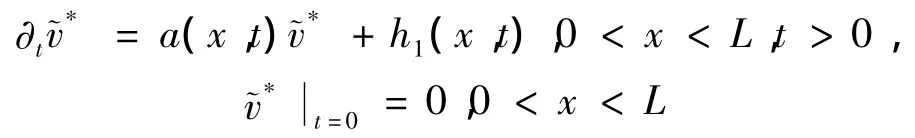
其中

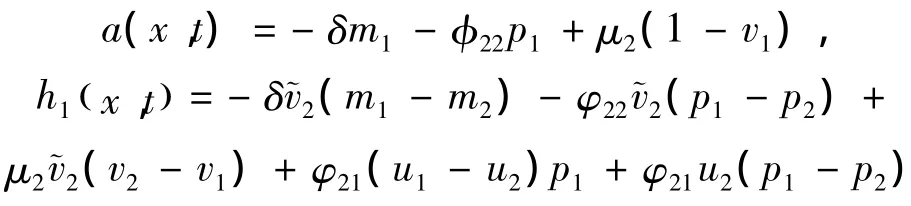
易得

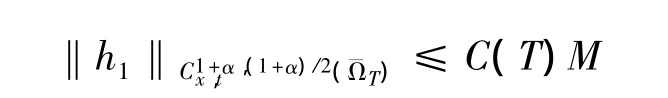
直接计算可得

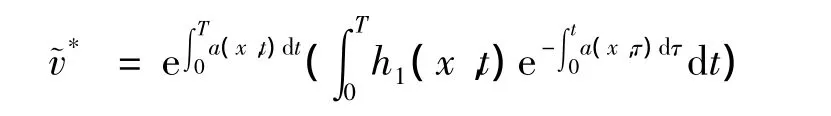
因此

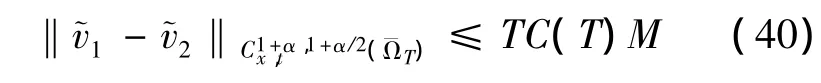
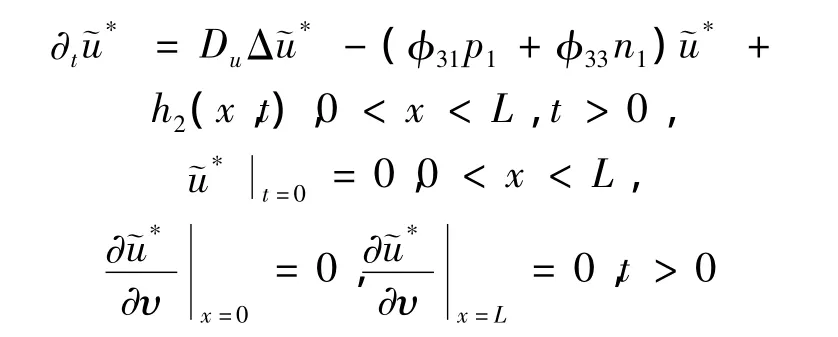
其中

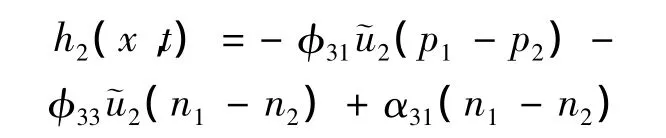
由引理2可得

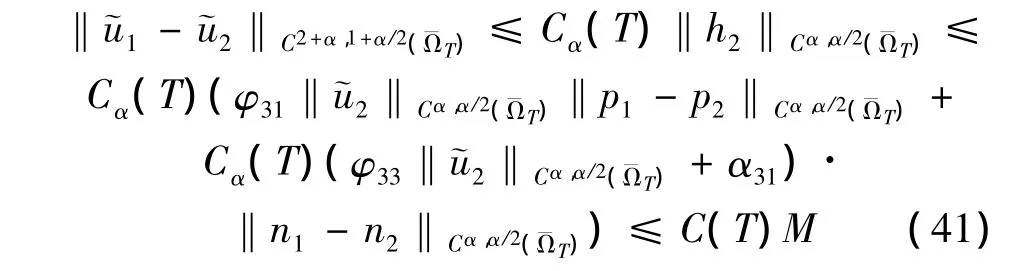
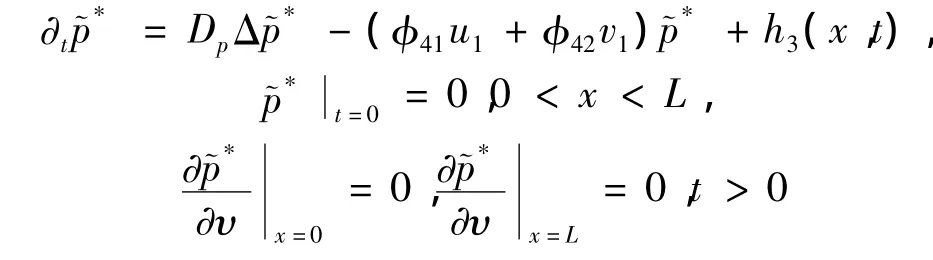
其中

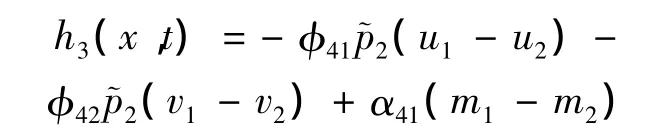
则根据引理2

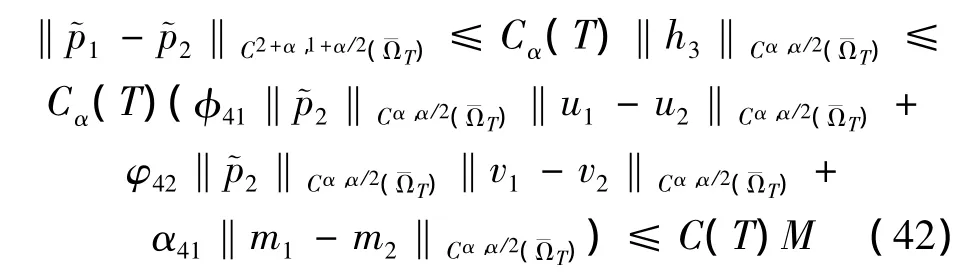
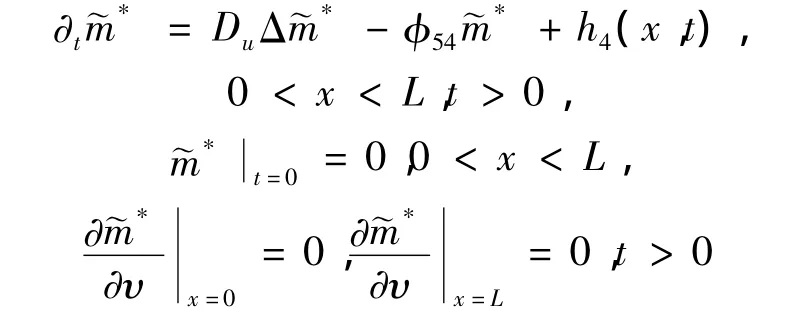
其中

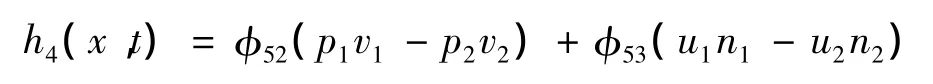
同理有引理2

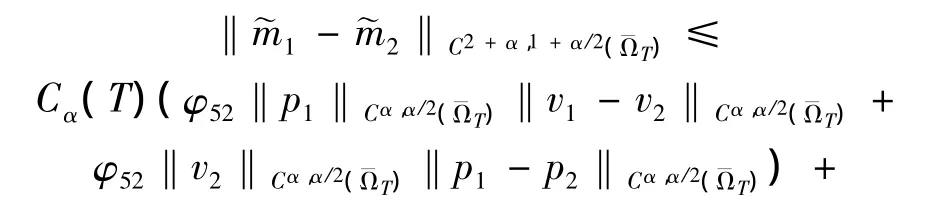
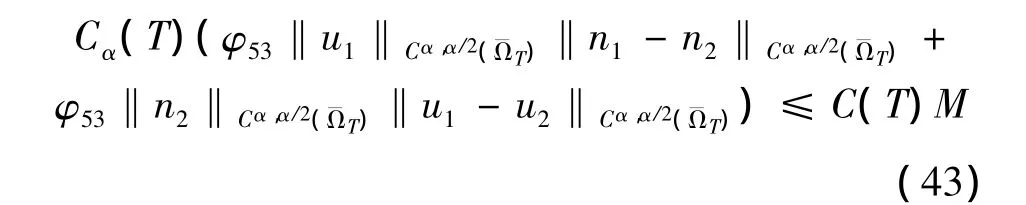
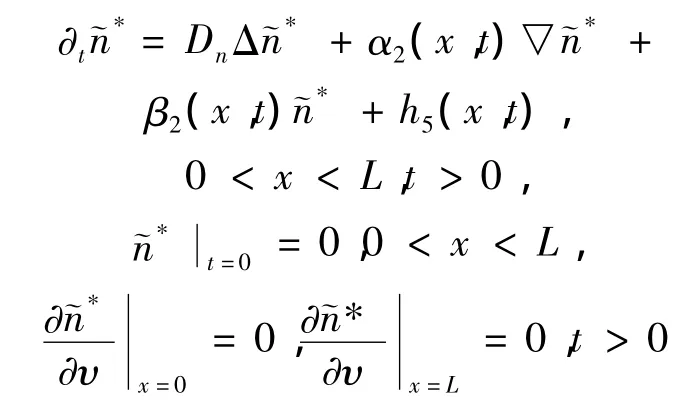
其中

则有引理2

综合 (40)－(44)，再由引理3可得

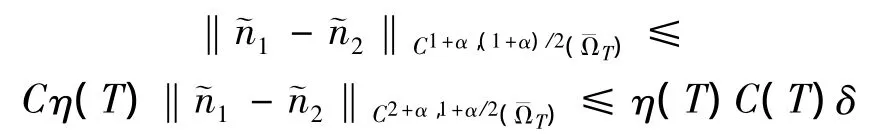
取T＞0充分小，使得 0＜max{η(T)C(T)，TC(T)}＜1，此时F为XM上的压缩映射。由Banach不动点定理可知，当T＞0充分小时，F存在唯一的不动点 (n，v，u，p，m)，它就是问题 (1)－(14)在区域ΩT中的唯一解。由证明过程可知T依 赖 于n(x，0)，v(x，0)，u(x，0)，p(x，0)，m(x，0)在空间C2+α(0，L)中的范数的上确界。上述结果可以总结为如下定理:

定理2 存在T＞0，使得问题 (1)－(14)在0＜t＜T时在区域ΩT内存在唯一解，T依赖于n(x，0)，v(x，0)，u(x，0)，p(x，0)，m(x，0) 在 空 间C2+α(0，L)中的范数的上确界。

3 整体解的存在唯一性

引理4 对 (1)－(14)有结论:

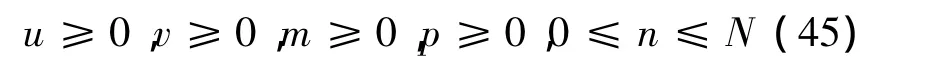
成立。

证明 ①对 (1)－(3)应用极值原理可得:0≤n≤Csup(n0)≡N。显然，u=0为 (6)－(8)的下解，故u≥0。

②下面证明v≥0，m≥0，p≥0.用反证法，假设p＜0，考虑m，p的抛物方程组

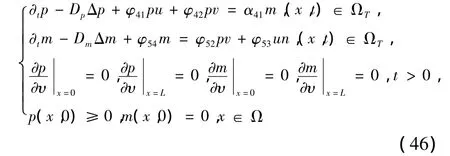
(i)当v≥0时，由抛物方程组的比较原理［8］，可知m≥0，p≥0，与p＜0矛盾;

(ii)当v＜0，p＜0时，由比较原理可知m≥0，也可推知p≥0，这也与p＜0矛盾。

由 (i)，(ii)综合可得p≥0，v≥0，m≥0。引理4得证。

引理5 对任意1＜k＜∞，存在一个依赖于T的常数Ck(T)满足

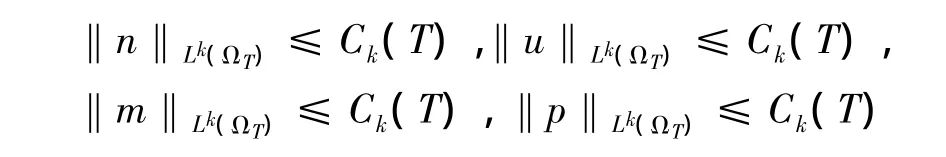
证明 由引理4，显然‖n‖Lk(ΩT)≤Ck(T)成立。①在方程 (6)两边同时乘以uk并且在ΩT上积分可得

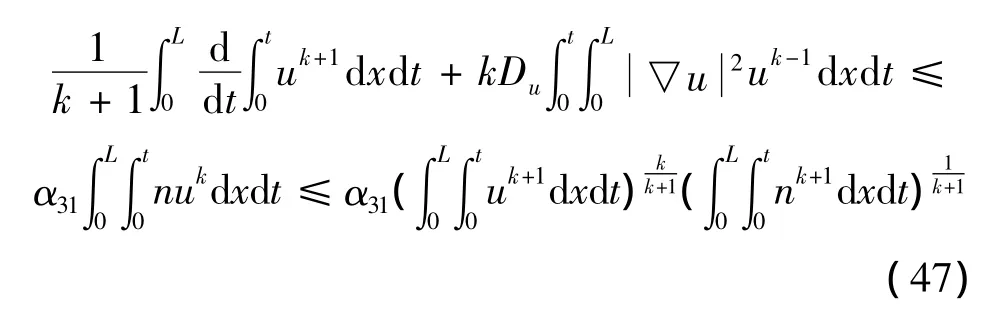
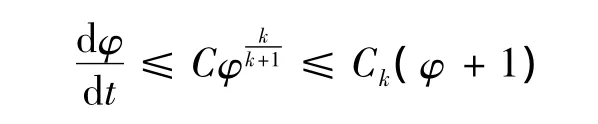
由Gronwall不等式，可得

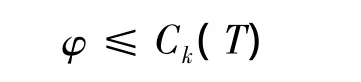
因此可得

②把式 (9)和式 (12)相加再乘以(m+p)k并且在ΩT上积分可得

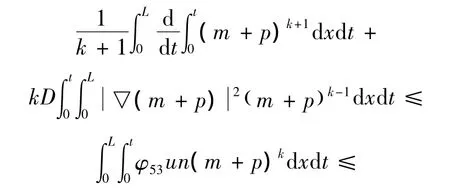
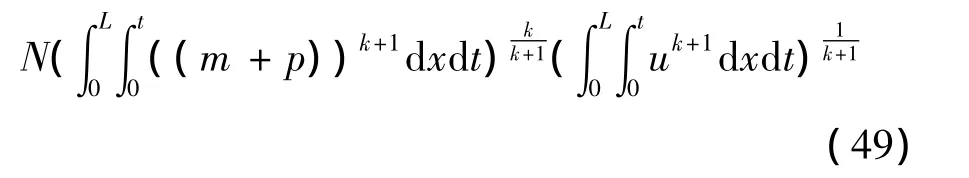
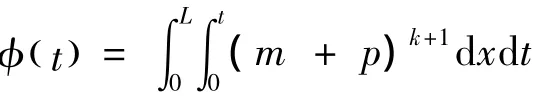
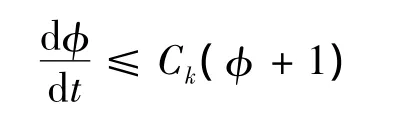
从而

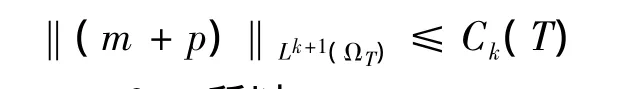
又m≥0，p≥0，所以

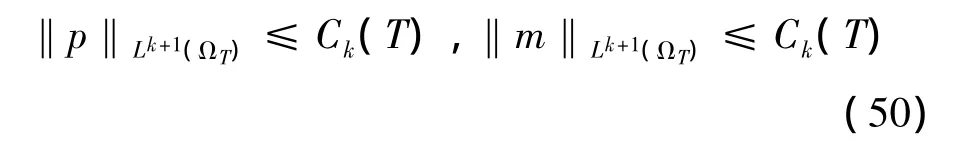
引理5得证。

引理6 对任意1＜p＜∞，存在一个依赖于T的常数Cp(T)满足

证明 ①对问题(6)－(8)应用引理1得

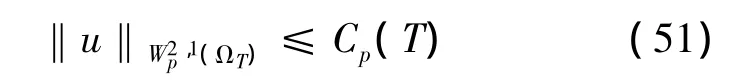
同理可得

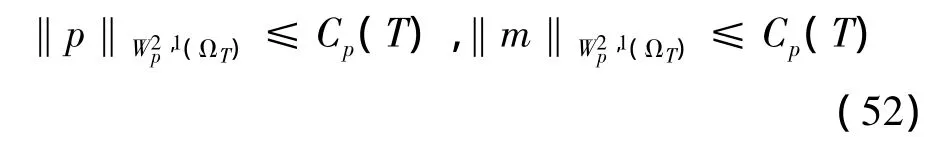
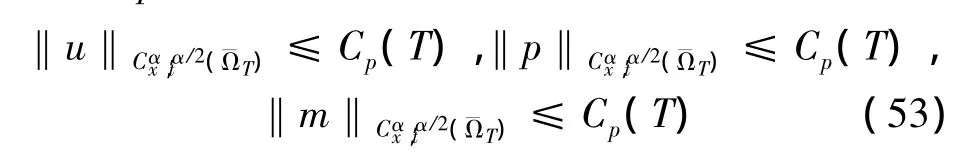
考虑问题 (4)－(5)，再用引理2，可知

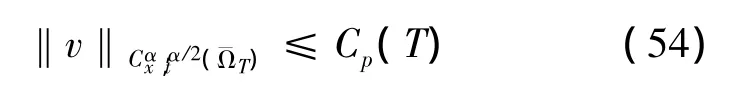
②问题 (1)－(3)可以写为如下形式:

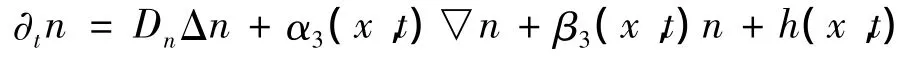
其中

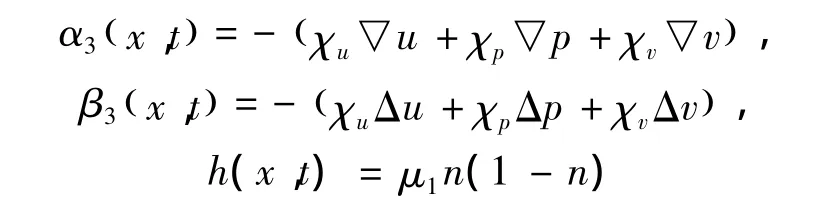
由引理5可知 β3(x，t)n+h(x，t)∈Lp(ΩT)，且α3(x，t)是连续有界函数，由引理1可得

引理6得证。

引理7 存在一个依赖于T的常数C(T)，满足

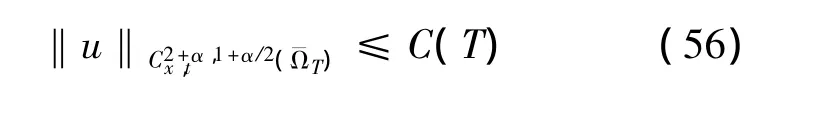
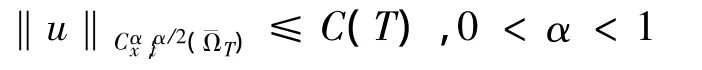
因此方程 (1)，(4)，(6)，(9)，(12)的系数满足引理2，因此可得

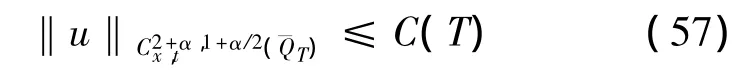
引理7得证

由定理2和引理7，可知定理1得证。

［1］ANDASARI V，GERISCH A，LOLAS G，et al.Mathematical modeling of cancer cell invasion of tissue:biological insight from mathematical analysis and computational simulation［J］.Math Biol，2011，23:141 －171.

［2］CHAPLAIN M A J，LOLAS G.Mathematical modeling of cancer invasion of tissue:the role of the urokinase plasminogen activation system［J］.Math Mod Meth in Appl Sci，2005，11:1685 －1734.

［3］叶其孝，李正元.反应扩散方程引论［M］.北京:科学出版社，2011.

［4］CUI S.Analysis of a free boundary problem modeling tumor growth ［J］.Acta Math Appl Sin Engl Ser，2005，21:1071－1082.

［5］LADYZENSKAJA O A，SOLONNIKOV V A，URAL'CEVA N N.Linear and quasilinear partial differential equations of parabolic type［M］.Translations of Mathematical Monographs，Am Math Soc，1968，23.

［6］FRIEDEMAN A，LOLAS G.Analysis of a mathematical model of tumor lymphangiogenesis［J］.Math Models Methods in Applied Sci，2005，15:95 －107.

［7］WEI X，CUI S.Existence and uniqueness of global solutions for a mathematical model of antiangiogenesis in tumor growth［J］.Nonlinear Analysis:Real World Applications，2008，9:1827 －1836.

［8］WEI X，GUO C.Global existence for a mathematical model of the immune response to cancer［J］.Nonlinear Analysis:Real World Applications，2010，11:3903 －3911.

［9］王术.Sobolev空间与偏微分方程引论［M］.北京:科学出版社，2009.