基于响应面法和遗传算法的孵育器多学科优化设计*
2013-09-13王钟周
王钟周
(苏州生物医学工程技术研究所,江苏 苏州 215163)
0 引 言
干式化学分析仪孵育器的结构优化设计涉及到高度关联和相互耦合的多个学科,为满足温度场分布和轻量化要求,研究者需采用多学科优化设计(MDO)方法[1-2]。目前,MDO方法主要应用在汽车设计领域[3-8],主要针对强度、刚度、动态性能和可靠性方面进行轻量化设计,研究者将MDO方法应用到医疗仪器的轻量化结构设计中,可用于实现温度场的优化设计。
本研究以温度均方差和平均温度作为衡量孵育器加热区域温度均匀性和温度高低的衡量指标[9-10],综合考虑结构轻量化、温度均匀性、温度恒定性之间的耦合关系,应用基于有限元模型的正交试验设计采集实验数据,采用响应面法(Response Surface Method,RSM)获取平均温度和温度均方差的响应模型,并以此为约束条件,应用遗传算法(Genetic Algorithm,GA)进行单目标和多目标优化设计[11-13]。
1 多目标优化问题及其求解
1.1 多目标优化问题
解决多目标多约束的优化问题称为多目标优化(Multi-objective Optimization)问题,多目标优化问题是在决策空间中搜寻一组由决策变量组成的向量,使得一组相互制约的目标函数同时取得最小值。其数学模型可表示为:
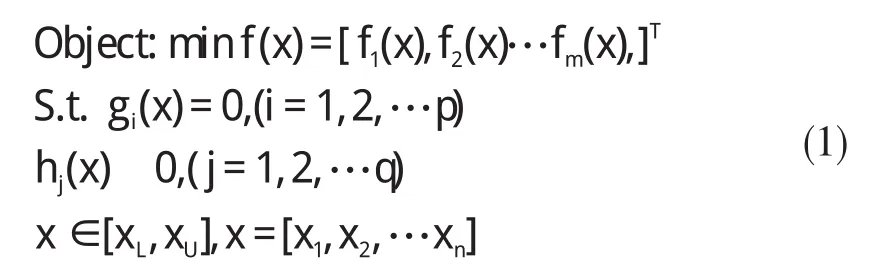
式中:f(x),g(x),h(x)—目标函数、等式和不等式约束函数;m,n,p,q—对应函数的个数;x—决策向量。
一般来说,多目标优化问题并不存在一个使多个目标函数同时取得最优值的解,而研究者只能根据设计要求从pareto解集中选取。
1.2 多目标优化问题求解
多目标优化问题一般有3种处理方法:加权求和法、主要目标法和智能算法。前两种方法将多个设计目标通过加权求和或者将次要优化目标转化为约束,从而将问题转化为单目标优化问题进行求解,所得结果均不是pareto解。遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,可以用于很好地解决单目标优化和多目标优化pareto解集的求解问题。
响应面法是基于试验设计和数理统计的建立经验数学模型的一种方法。本研究通过正交试验对设计空间进行均匀数据采集,获取响应面模型,以此代替有限元模型,提高了运算效率。二次多项式响应面模型是应用最为广泛的一种近似逼近模型,其基本形式为:

式中:y—响应面拟合函数;xi—设计变量;β0,βi,βi i,βi j—待定系数,通过最小二乘法确定。
本研究综合运用响应面法和遗传算法减少有限元分析的工作量,进行复杂的多耦合场优化设计,弥补有限元分析在多学科优化设计中的不足。
2 孵育器温度场的单因素分析及其数学模型
2.1 孵育器有限元模型
恒温孵育器是干式化学分析仪的重要组成部分,几何模型如图1所示。
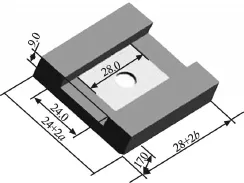
图1 孵育器几何模型
试剂片加样后被运送到孵育器进行加热,待反应完后,由光学系统检测吸光度值,研究者根据朗伯比尔定律可以计算出相应物质的浓度。
孵育器由两片对称布置的半导体制冷器采用PID控制进行加热,有效消除环境因素对孵育器温度的影响,可看作稳态温度场。
本研究选用SOLID90实体单元划分网格,为简化孵育器有限元模型,作以下假设:半导体制冷器加热功率等效为均匀热流密度施加在侧面,孵育器与支撑板和盖板接触面按绝热处理,其余表面按自然对流传热处理;孵育器工作过程中热边界条件稳定,视为稳态传热过程;忽略孵育器圆角,倒角,螺纹孔等局部特征;孵育器材料导热性各向同性,环境温度和对流系数视为常量,辐射换热忽略不计;半导体制冷器视为均匀热源施加在孵育器两个侧面;孵育器的上盖和底座材料均为聚甲醛,其接触热阻很大,它们之间的热通量忽略不计。
2.2 孵育器温度场的数学模型
铝导热系数λ=144 W/(m·℃),太大的导热系数对温度均匀性影响很小,考虑铝的密度较小,本研究中孵育器材料选为2A12。通常干式化学分析仪工作环境较为稳定,故笔者将表面传热系数和环境温度视为常量。本研究选取孵育器壁厚a、长度b和热流密度q作为设计变量,以平均温度μ、温度均方差σ和最大温差δ作为优化目标,采用正交表L16(45)进行试验。
设计变量水平如表1所示。
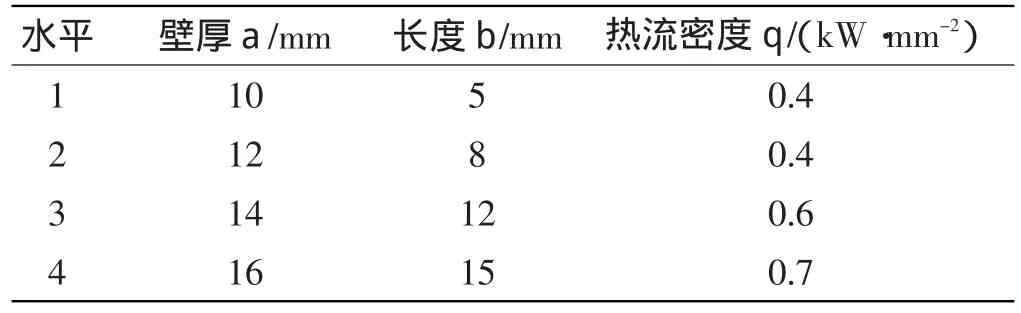
表1 设计变量水平表
本研究采用Matlab数理统计工具箱对实验数据进行拟合,得到平均温度及温度均方差的响应曲面模型。经检验,模型满足显著性检验,拟合度R20.99,且最大相对误差不超过1%。
以平均温度响应曲面为例,q=48 0W/mm2和b=6mm时平均温度响应面模型如图2、图3所示。由此可见,平均温度μ与壁厚a和长度b成负相关关系,和热流密度q成正相关关系,与单因素分析规律相同,从而说明了该响应模型的正确性。
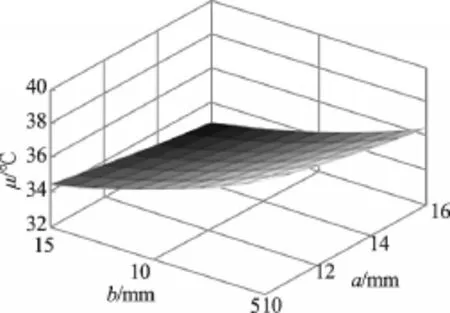
图2 q=48 0W/mm2时,平均温度响应面模型
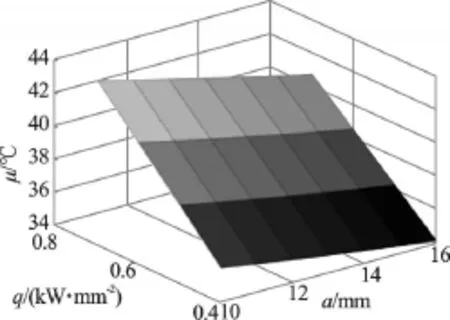
图3 b=6mm时,平均温度响应面模型
3 孵育器结构优化设计
在表面响应模型的基础上,本研究应用遗传算法分别对孵育器进行轻量化设计,将所得结果与有限元优化结果进行对比,验证该方法的可行性;通过多目标遗传算法(Multi-Objective Genetic Algorithm,MO⁃GA)对孵育器进行多目标优化设计,求得pareto最优解集,为设计提供备选方案。
3.1 孵育器轻量化设计
本研究在目标区域温度和温度均匀性都满足要求的情况下,以“质量最小,即体积最小”为优化目标进行设计。优化设计的数学模型可以表示为:

其中:i=1,2,3;x=[x1,x2,x3]=[a,b,q]。
本研究分别采用ANSYS一阶优化算法和Matlab遗传算法工具箱进行优化,结果如表2所示。通过表2可以发现,两种方法结果相近,表明该方法可以替代有限元模型进行优化设计。笔者针对Matlab优化参数进行有限元分析,优化后的温度场平均温度满足要求,均匀性得到很大改善,且质量减少约14%。
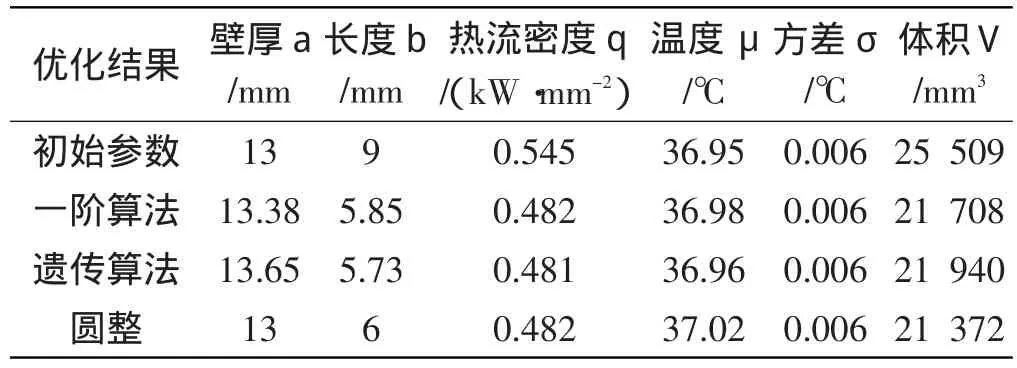
表2 优化结果对比
3.2 孵育器结构多目标优化
孵育器的多目标优化问题可以描述为:
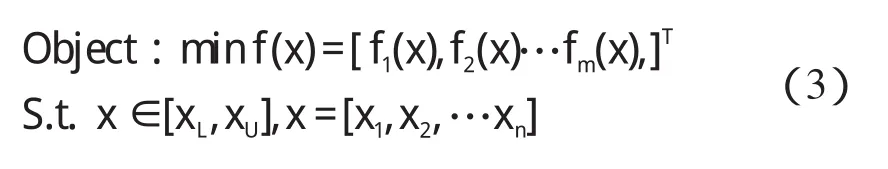
式中:x=[x1,x2,x3]=[a,b,q];fi(x)—设计目标,可以是质量、平均温度、温度均方差。
根据不同的设计需求,本研究可以选择适当的设计目标,应用多目标遗传算法求得相应的pareto解集。两优化目标的pareto front曲线和三优化目标pa⁃reto最优解集如图4、图5所示。

图4 两优化目标pareto front曲线
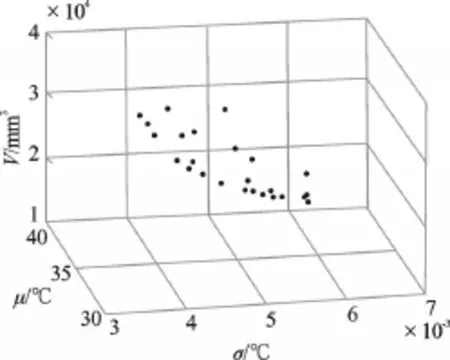
图5 三优化目标pareto最优解集
由图可知,对于多目标问题,各设计目标之间是相互制约的,无法实现使各目标同时取得最优解。一般情况下,研究者可以根据设计要求进行适当的取舍,从pareto解中选取合理的设计参数。
4 结束语
(1)本研究采用正交试验设计采集数据,通过响应面法获取设计目标的响应面模型,该方法可以用来准确描述设计变量与设计目标之间的关系。
(2)本研究以响应面模型替代有限元模型,应用遗传算法进行优化设计,其优化结果与有限元模型结果基本一致。
(3)在实际应用中,该方法中的边界条件参数尚需实验测定。对于复杂耦合场的多学科优化设计,研究者可以用该方法取代有限元模型进行求解,避免了对有限元软件的二次开发,提高了求解效率。
(References):
[1] YANG R J,GU L,THO C H.Multidisciplinary Design Opti⁃mization of a Full Vehicle with High Performance Comput⁃ing[C]//The 42nd AIAA/ASME.ASCE/AHS/ASC Struc⁃tures,Structura lDynamics,and Material Conference and Ex⁃hibit.Seattle:[s.n.],2001.
[2] KODIYALAM S,YANG R J,GU L,et al.Multidisciplinary design optimization of a vehicle system in a scalable,high performance computing environment[J].Structural and Multidisciplinary Optimization,2004,26(3-4):256-263.
[3] 张 勇,李光耀,孙光永,等.多学科设计优化在整车轻量化设计中的应用研究[J].中国机械工程,2008,6(7):877-881.
[4] KODIYALAMS,YANG R J,GU L,et al.Multidiscipli-nary design optimization of a vehicle systemin a scalable,high performance computing environ-ment[J].Structural and Multidisciplinary Optimization,2004,26(4):256-263.
[5] 胡朝辉,成艾国,王国春,等.多学科优化设计在拼焊板车门轻量化中的应用[J].中国机械工程,2010,21(4):495-499.
[6] 魏璐璐,左正兴,向建华.基于ISIGHT的曲柄连杆机构多学科优化[J].机电工程,2011,28(12):1436-1439.
[7] 许 志,李 芳.基于灵敏度分析的发动机连杆优化设计[J].机电工程,2011,28(9):1052-1056.
[8] 宁晓斌,姜 健,谢伟东.基于汽车悬架的多目标优化方法的研究[J].机电工程,2011,28(2):165-171.
[9] 程雪涛,徐向华,梁新刚.温度场与温度梯度场的均匀化[J].中国科学(E辑:技术科学),2009,39(10):1730-1735.
[10] 乔赫廷,张永存,刘书田.散热结构拓扑优化目标函数的讨论[J].中国机械工程,2011,9(22):1112-1117.
[11] LIU Hai-lin,WANG Yu-ping,CHENG Yiu-ming.A multi-objectiveevolutionary algorithm using min-max strate⁃gy and sphere coor-dinate transformation[J].Intelligent Automation and SoftComputing,2009,15 (3) :361-384.
[12] 王永泉,陈花玲,贺学明.基于遗传算法的静电反馈式微传感器多目标优化[J].西安交通大学学报,2006,40(11):1305-1309.
[13] 饶 江,胡树根,宋小文,等.汽车悬架优化过程的Pareto最优解[J].机电工程,2010,27(6):28-31.
