钢轨铝热焊接接头性能的有限元分析

叶 渊，潘文彬，杨 韬，宋家旺

（1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.吉林大学 超塑性与塑性研究所，吉林 长春 130012）

0 引 言

无缝线路是轨道结构技术进步的重要标志，也是轨道结构的最优选择。钢轨焊接是无缝线路的基础，是铺设无缝线路的一个重要环节，焊接质量是保证无缝线路正常运行的关键[1]。钢轨焊接包括闪光焊、气压焊、电弧焊和铝热焊，铁路上常用的钢轨铝热焊，其实质是冶金铸焊，焊接接头力学性能在4种焊接技术中最差，是无缝线路最薄弱的环节。

钢轨焊接尤其是现场铝热焊接（如断轨抢修、应力放散等），在进行完焊接不久之后焊接接头就会开始服役，因此，焊接过程与焊接接头的力学性能是联系在一起的。以往，大多数文献关于钢轨焊接结构的分析都是将焊接方法与焊接结构的力学性能在某种程度上独立开来进行的[2-5]，这就从一定程度上降低了分析的精确性，与焊接结构的实际状况有差距，因此分析结果有一定的误差。

本研究基于Hertz接触理论，加入钢轨铝热焊接过程数值模拟结果，并采用车辆-轨道耦合动力学方法，求解带有焊接接头短波不平顺的轮轨接触关系，最后，结合铝热焊模拟结果和求解的轮轨接触关系建立焊接接头轮轨接触弹塑性有限元模型，并进行分析。

1 钢轨铝热焊接

钢轨铝热焊的原理如下：将配好的铝热焊剂在坩埚内用高温火柴引燃使之发生氧化还原反应，反应生成的高温铝热钢水通过砂型浇注系统注入到由砂型和待焊钢轨组合形成的型腔内，由高温钢水产生的热量将钢轨端面熔化，经冷却和凝固将钢轨焊成一体。整个过程包括预热、浇注和凝固3个阶段[6]。

本研究采用侧顶式浇注系统，用CFD软件Fluent进行铝热焊接模型的建立及焊接热传递过程的数值分析。分析过程采用随温度变化的导热系数和比热，相变过程通过指定热焓将熔合潜热考虑在内[7]。由于篇幅有限且热过程模拟不是本研究讨论的重点，在此不作详述，仅给出模拟的输入类型参数以及模拟结果。模拟类型参数如表1所示，模拟结果如表2所示，模拟结果将作为后文有限元模型的输入条件。

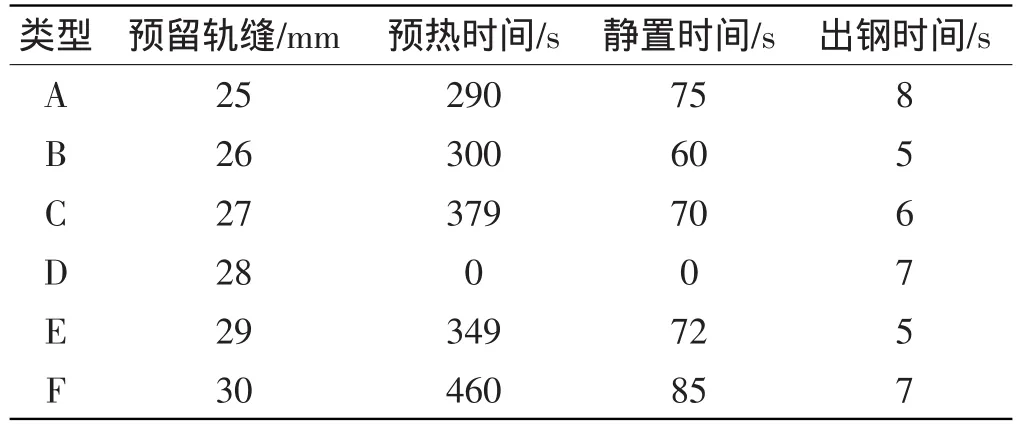
表1 铝热焊接热传递模拟的输入参数

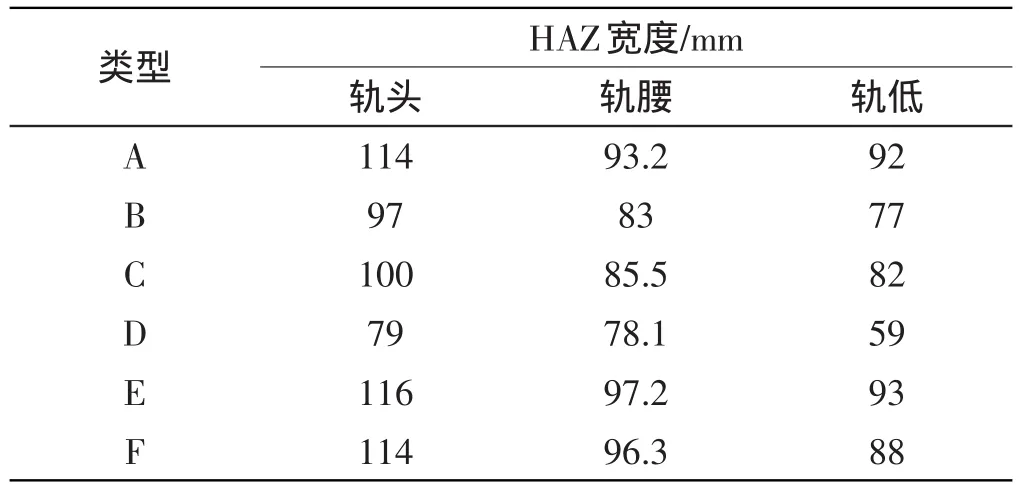
表2 模拟结果

2 轮轨接触理论

2.1 Hertz接触理论

Hertz接触理论是建立在无摩擦的弹性接触面上的[8]，为了计算局部变形，本研究引入了如下假设：①轮轨接触表面连续，并且是非协调的；②接触体变形很小；③每个弹性体可被看作是一个半空间；④接触表面光滑。Hertz接触理论得出的两物体的接触变形为椭圆形接触斑，最大接触压力为：

式中：P—轮轨法向接触力；a，b—椭圆接触斑的长短轴半径。

进而椭圆形接触区的接触压应力的分布为：

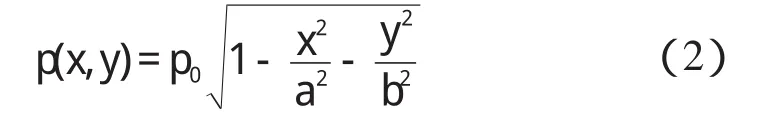
且垂向最大接触应力σmax为：

全滑动工况下的纵向切力可以在求出p(x,y)之后，通过下式求得：

式中：μ—接触面的摩擦系数。

2.2 车辆-轨道耦合动力学方法

翟婉明教授[9]指出，车辆-轨道耦合动力学能更好地体现轮轨相互作用的本质，且由于钢轨焊接接头剥离、失效等问题主要是由轮轨相互作用引起的，而钢轨采用Timoshenko梁模型更能反映钢轨振动中的高频成份，同时其主要研究存在短波不平顺时的轮轨接触状态对焊接接头性能的影响，因此本研究采用考虑钢轨焊接接头短波不平顺的基于Timoshenko梁的车辆-轨道耦合动力学方法。由于车辆-轨道耦合动力学模型以及推导公式非常繁杂，本研究不作详述，这里仅给出焊接接头存在不平顺时的车辆-轨道耦合动力学特性。

轮轨法向冲击载荷由赫兹非线性弹性接触理论来确定，考虑钢轨焊接接头处接触表面短波不平顺，轮轨法向冲击载荷的计算由下式确定：

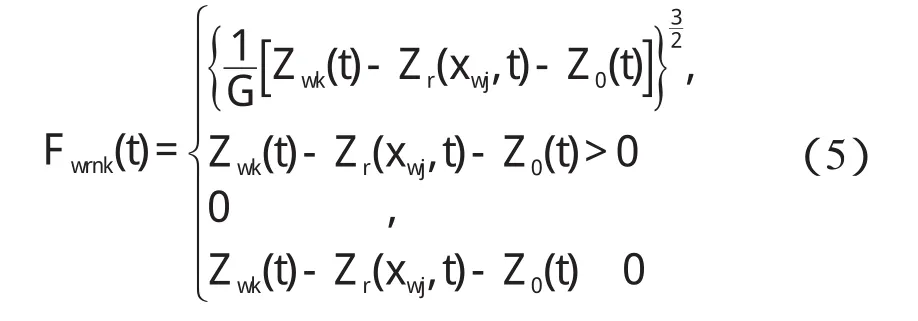
式中：Zwk(t)—车轮k(k=1,…,8)的位移，Zr(xwj,t)—第i(i=1,…,8)个车轮作用点处钢轨的位移，Z0(t)—钢轨接触表面焊接接头不平顺随时间函数与轮轨法向静压缩量之和。

轮轨接触常数G(m/N23)与车轮和钢轨接触面外形有关，这里，参数G的求解参照文献[10]，最后代回式（5）可求得轮轨的法向冲击载荷以及接触斑的长、短轴半径。

2.3 求解结果

2.2节所建立的车辆-轨道耦合方程和焊接接头不平顺时的轮轨间的相互作用关系以及边界条件联立起来将是一个大型的非线性微分方程，本研究采用文献[9]提出的新型显示积分法进行求解，这种方法具有计算速度快、稳定性高、收敛好的优点。车辆取轴重15 t，时速200 km/h～300 km/h的高速铁路客车，磨耗型车轮踏面；钢轨取普通土路基上的直线段有碴轨道，60 kg/m钢轨，混泥土轨枕，1 760根/千米，轨枕、扣件提供的垂向刚度45 kN/mm，纵向、横向刚度均为20 kN/mm。由于短波不平顺对轮轨的冲击远大于其他不平顺情况，本研究只考虑短波不平顺时的动力响应。焊接接头短波不平顺取典型的不平顺波长λ=0.1 m，波深δ=0.3 mm，求解结果如下：

当车速在200 km/h～300 km/h变化时，轮轨法向冲击力的峰值随着速度的增加而增加，如图1所示。距离对轮轨法向力的影响如图2所示。图2中，横坐标代表处于两个轨枕之间的焊接接头的焊缝中心线距离较近轨枕中心线的距离，由图2可知，距离越远，轮轨法向冲击载荷的峰值越小。

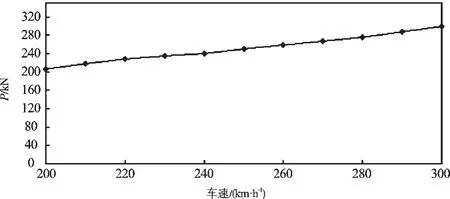
图1 车速对轮轨法向力的影响

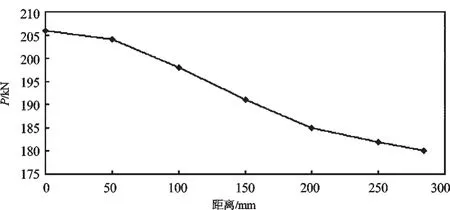
图2 距离对轮轨法向力的影响

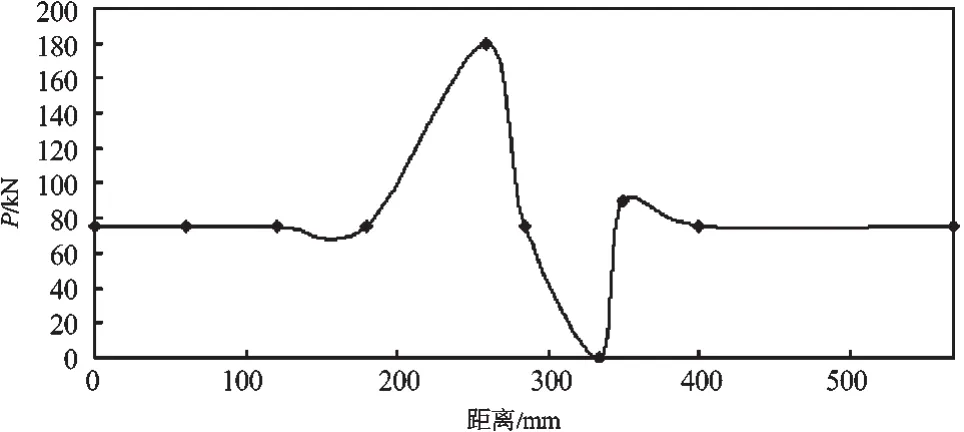
图3 法向冲击载荷的变化规律

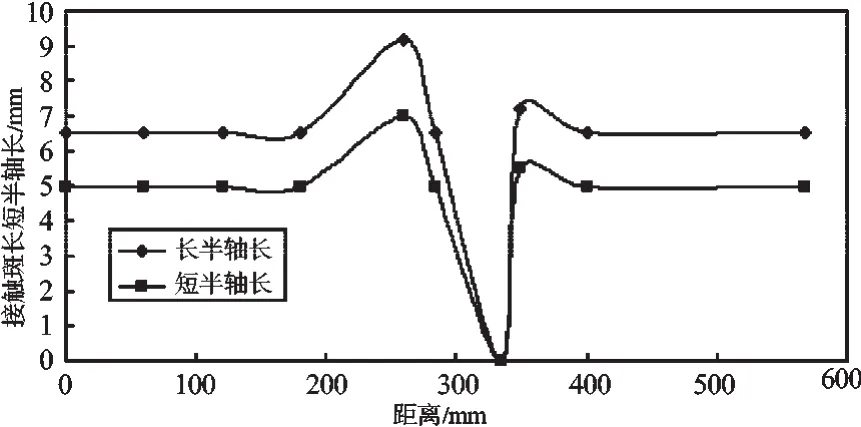
图4 接触斑长短半轴的变化规律

当车速为200 km/h，焊接接头中心线位于相邻两轨枕间的轨段正中间时，随距离的改变，两轨枕间的法向力变化规律如图3所示，同时，接触斑长短半轴长度a，b变化规律如图4所示。由图3和图4可知，当轮轨接触位置处于接头不平顺的0.25个波长位置时，法向力达到最大值，且接触斑面积最大；在距离焊缝中心65 mm处，法向力又出现了一个小波峰，这是由于车辆前转向架的第二轮对通过不平顺接头时对第一轮对产生的影响。图1～图4所得结果将作为下文的输入条件。

3 有限元模型及结果分析

3.1 有限元模型

结合前两节求解的各项参数作为本节的输入条件，本研究建立了无缝钢轨铝热焊接接头的轮轨接触弹塑性有限元分析模型。本研究采用ABAQUS建立有限元模型，钢轨模型取相邻3根轨枕间的轨段[11]，焊接接头位于2、3轨枕间轨段的正中间，且焊缝宽度取为25 mm，HAZ宽度为100 mm，不平顺位于焊接接头上，轨枕和扣件采用弹簧单元来等效。

本研究采用von-Mises屈服准则来判断接头材料是否进入塑性区：

式中：σs—材料单向拉伸的屈服应力，σi(i=1,2,3)—主应力。

设钢轨材料具有双线性循环硬化特性[12-15]，弹性模量取210 000 MPa，强化模量取21 000 MPa，钢轨母材的屈服强度σs取为520 MPa，而铝热焊接接头的屈服强度相对较低，通常为母材的80%左右，这里取为416 MPa。在不影响分析精度的前提下，为了缩短计算时间，本研究将焊缝和热影响区部分以及轮轨接触区设置为塑性材料，总长为439 mm，将其余部分设置成线弹性材料[16]。在施加法向载荷时，本研究将椭圆形分布的接触力通过随时间变化的面力幅值函数施加在接触面上，载荷增量步为0.2，接触斑每隔一个网格滚动一次，以此来模拟车轮在钢轨上的滚动。轮轨处于全滑动接触时，轮轨间的摩擦系数取为0.3，切向力大小及分布由式（4）求得，切向力的施加方法同上。边界条件：除将钢轨底部轨枕和扣件等效为弹簧单元之外，本研究在钢轨左、右两个端面施加纵向的位移约束，限制钢轨的刚体位移。网格划分时，焊缝、热影响区、母材网格由细到粗过度，而轮轨接触区由于变形较大，网格划分较细，接触区纵横向种子间隔1 mm，垂向网格由细到粗过度，粗细比为4；由于接触区与非接触区网格密度过渡大，接触面采用tie约束，并且将接触区表面作为从面，非接触区表面作为主面，以消除交界面上的额外应力。

本研究采用C3D8R类型的8节点线性六面体减缩积分单元，共生成85 668个节点和68 914个单元。网格划分如图5所示。

图5 焊接接头网格划分图

3.2 结果分析

本研究求得的纯滚动接触工况下的最大垂向应力为σ22=1 331.2 MPa，与式（3）所得的法向最大压力1 334.5 MPa基本相等，由此可见，本研究的有限元模型是可行的。纯滚动工况下的焊接接头Mises应力、PEEQ分布云图如图6所示，针对其他情况只给出对比曲线图及数据表格。

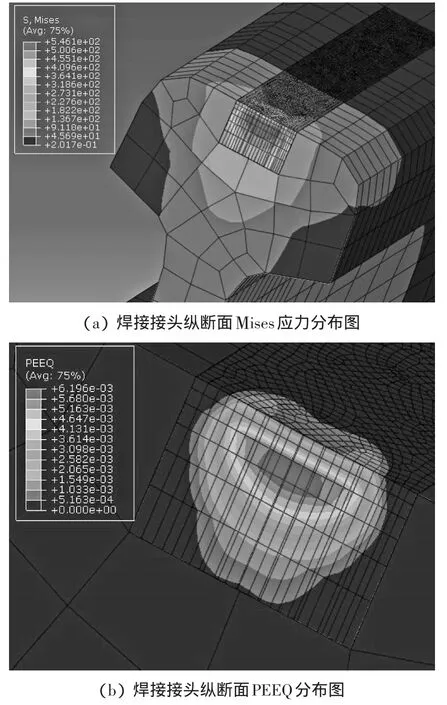
图6 纯滚动时焊接接头Mises和PEEQ分布图

图7 纯滚动时Mises应力和PEEQ随深度变化图

图8 全滑动时Mises应力和PEEQ随深度变化图

纯滚动和全滑动工况下焊接接头处Mises等效应力和等效塑性应变随距离轨头表面的深度变化的双轴曲线图如图7、图8所示。由图7可知，当轮轨纯滚动接触时，随着深度的增加，焊接接头处的Mises应力和PEEQ均先增大后减小，且最大值均位于轨头表面以下4.1 mm深处，可见该处为最危险区域，裂纹很有可能从此处萌生。当车辆处于紧急制动或启动加速空转时，轮轨之间会处于全滑动接触状态，由图8可见最大等效应力为665.5 MPa，为纯滚动时的1.22倍，最大PEEQ为0.011 92，为纯滚动时的1.92倍，且求得的最大残余变形为0.078 5 mm，为纯滚动时的2倍，且三者的最大值均位于轨头表面（即深度0 mm处）。可见，轮轨处于全滑动接触时，由于存在较大的切向力，法向力和切向力的共同作用使得等效应力、等效塑性应变和残余变形均向钢轨表面移动，也就是说，全滑动时，焊接接头短波不平顺使钢轨接头表面更容易发生压溃、剥离甚至接头失效。因此，在车辆运行中，应尽量避免全滑动情况的发生。

纯滚动工况下，改变HAZ宽度、焊缝中心与较近轨枕的距离以及车速时的轮轨动力响应如表3～5所示。由表3～5可知，PEEQ、残余变形以及最大Mises应力随着HAZ宽度的改变没有明显变化，随着距较近轨枕距离的减小而增大，随车速的增大而增大。

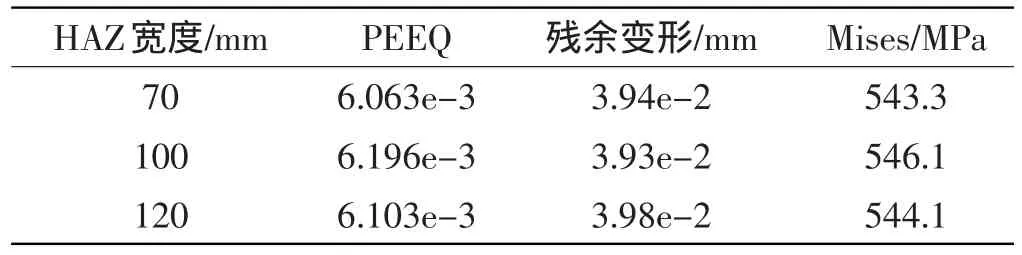
表3 HAZ宽度变化时的轮轨动力响应

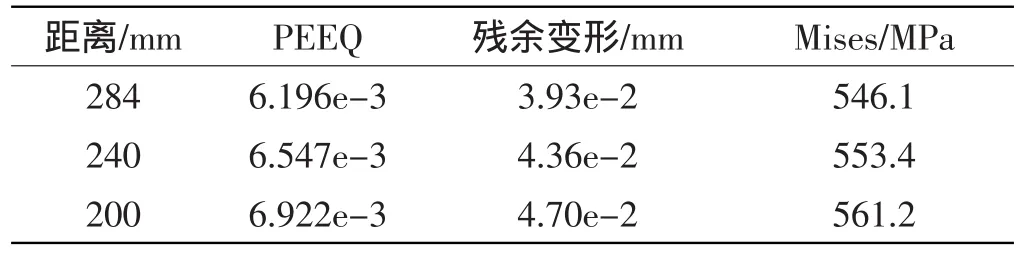
表4 距离变化时的轮轨动力响应

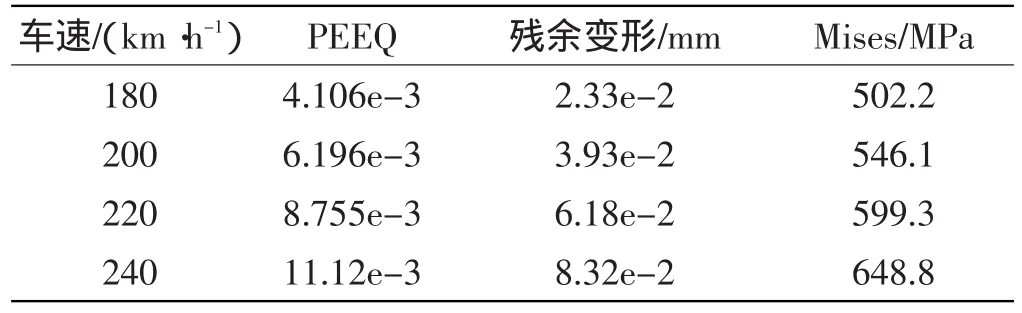
表5 车速变化时的轮轨动力响应

4 结束语

本研究通过对钢轨铝热焊接接头性能的有限元分析可知，当焊接接头存在短波不平顺时，在纯滚动工况下，接头表面以下4.1 mm深度处为危险区域，裂纹可能从此处萌生；在全滑动工况下，最大等效应力、等效塑性应变和残余变形均向轨头表面移动，可能造成焊接接头表面剥离、压溃乃至接头断裂，危及行车安全，所以应尽量避免车辆紧急制动以及启动加速空转的发生；在进行铝热焊接时应尽量将接头焊缝设置在距离邻近轨枕较远处，同时，要不断提高铝热焊接工艺，改善接头性能，减少由于接头塑性变形导致的永久变形，从而避免由于车轮反复碾压引起接头短波低踏不平顺。

今后的研究可以通过结合更加具体的轮轨接触模型（如加入道床、路基模型），同时结合铝热焊接接头的硬度、微观组织等真实接头特性来进行模拟，以便得到更加精确的结果。

（References）：

[1] 高文会，李 力，丁 韦.钢轨焊接质量的现状及对策[J].中国铁路，2004（2）：32-34.

[2] 许玉德，周 宇.钢轨焊接接头最危险应力确定[J].同济大学学报：自然科学版，2003，31（2）：170-173.

[3] CHEN Yi-ren.A Heat Transfer Modeling Study of Rail Thermite Welding[D].Urbana：University of Illinois at Ur⁃bana-Champaign，2004.

[4] 高松福.提高钢轨铝热焊接头性能研究[D].北京：中国铁道科学研究院，2010.

[5] 肖广文.钢轨焊接接头伤损分析[D].成都：西南交通大学机械学院，2009.

[6] 刘书华.铁路焊接技术的发展及展望[C].铁路焊接技术交流会论文集，大连：[出版者不详]，1997：9-13.

[7] YU K O.Modeling for Casting and Solidification Processing[M].Boca Raton：CRC Press Inc.，2002.

[8] 张 军.基于有限元法的轮轨蠕滑理论研究[D].大连：大连理工大学机械学院，2003.

[9] 翟婉明.车辆-轨道耦合动力学[M].3版.北京：科学出版社，2007.

[10] 金学松，刘启跃.轮轨摩擦学[M].北京：中国铁道出版社，2004.

[11] 王勖成.有限单元法[M].北京：清华大学出版社，2003.

[12] 张立明.轮轨接触应力与钢轨波磨分析[J].西南交通大学学报，2003，38（1）：34-37.

[13] 屠胜立，张 宪.膜式水冷壁焊接变形热弹塑性有限元分析[J].轻工机械，2011，29（15）：11-13.

[14] 朱红建.基于ANSYS的粉料罐有限元分析及结构优化[J].现代制造技术与装备，2011（2）：57-59.

[15] 杜 星，郭 俊，陈 婧，等.地铁线路控制钢轨波磨的钢轨打磨技术应用研究[J].机械，2011，38（10）：9-13.

[16] 石亦平，周玉蓉.ABAQUS有限元分析实例详解[M].北京：机械工业出版社，2006.