一类状态脉冲不育控制的单种群模型

李晓霞

(运城学院应用数学系，山西 运城 044000)

一类状态脉冲不育控制的单种群模型

李晓霞

(运城学院应用数学系，山西 运城 044000)

建立了一类状态反馈脉冲控制的不育单种群模型，当害鼠的数量达到经济危害水平时，通过灭杀，从而控制种群数量的增长。首先利用微分方程几何理论和后继函数的方法得到系统阶1周期解得存在性，并给出了阶1周期解得渐近稳定性的充分条件。

状态脉冲；不育；阶1周期解

健康的生态系统是稳定、具有活力、有自调节能力的系统。系统为每一种植物、动物、微生物都准备了它们所需要的食物和生存空间，任何一种植物、动物、微生物在系统中都有自己的位置；它们的存在不仅无害，还有助于维持整个系统的健康发展。然而在自然变化过程和人类不合理活动的影响下，系统平衡常常会被打破，有些生物会偏离它们原来的动态轨迹，发生种群数量的爆发，破坏生态系统的结构和功能，威胁人类的利益，从而变成有害生物，如果是鼠类，则称为害鼠。害鼠的综合治理早在20世纪60年代后期收到了人们的普遍关注，控制害鼠的方法分为化学控制，不育控制，生物防治，机械防治，物理防治等。化学控制会污染环境破坏生态系统的稳定性。近年来，不育控制下的数学模型已受到广大学者关注[1-8]，研究了不育控制下的害鼠种群模型。但是，不育控制下种群的减小是一个缓慢的过程。

在害鼠防治中，不应当见鼠就治，而应当考虑充分考虑作物的补偿作用，有研究结果表明，草木受害后不一定就造成生长损失。相反，在一定程度上，可增加草木生长量。当受害程度达到补偿点时，草木生长率最大，超过补偿点以后，才出现生长损失。因此，有害鼠不一定造成危害。从而在海鼠防治中，应当充分考虑作物的补偿作用，确定害鼠的经济危害水平，制定准确的经济阈值。基于此想法，本文建立一类不育控制下状态脉冲收获的害鼠防治模型，即当害鼠数量达到经济危害水平h，实施灭杀控制，在小于经济危害水平h实施不育控制，关于带有状态依赖的脉冲微分方程[9]。

1 模型

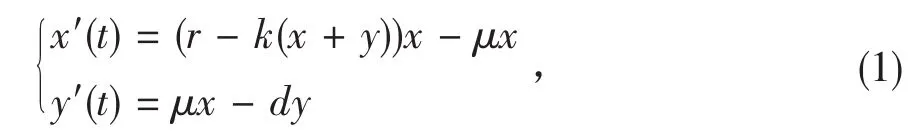
其中x(t)，y(t)分别是害鼠可育者，害鼠不育者在时刻t的密度。近几年，有关学者对不育控制下的种群模型做了不少的研究，但关于状态反馈脉冲不育控制的单种群模型还没有见到，因此研究以下系统：

在文献[8]中，讨论了不育控制下的单种群模型：这里所有系数均为非负的，μ是每次投放不育剂使得害鼠可育者变为不育者的比例。h定义为经济危害水平中导致经济危害的害虫数量。

△x(t)=x(t+)－x(t)，△y(t)=y(t+)－y(t)，

p是实施灭杀控制时候的被捕获的数量比例。

对系统(1)有以下结论：

定理1当r-μ≤0时，系统(1)零平衡点(0，0)是全局渐近稳定的；

2 阶1周期解的存在性

主要利用微分几何理论和后继函数的方法讨论状态依赖的脉冲微分系统(2)的阶1周期解的存在性。

为了使用方便，下面给出一些记号和定义。脉冲集为

脉冲函数为

I：(x，y)∈M→((1-p)h，(1-p)y)。

相集

N＝I(M)={(x，y)∈

x′(t)=0，y′(t)=0，

N1={(x，y)∈R2+|x=(1-p)h，y≥0}。

定义对于任意的点P∈N1，系统(2)存在过点P的轨线Γ，它与脉冲集M交与点P1，=I(P1)∈N，令yp+1，yp1，分别表示，P1与x轴距离，g(P)= yp+1-yp1那么g(P)就是点P的后继函数，其中称为点P的后继点。

定理2当r-μ＜0时，系统(2)的平衡点(0，0)是全局渐近稳定的。

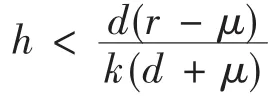
(Ⅰ)点B+与点A重合；(Ⅱ)点B+在点A正上方；(Ⅲ)点B+在点A正下方。

当B+与点A重合时，显然轨线Γ1就是系统(2)的阶1周期解。下面证明在(Ⅱ)，(Ⅲ)这每种情形之下，都存在阶1周期解。

当B+在A正下方，在点A的正下方且充分接近取一点C′。经过C′的轨线设其为，根据微分方程解函数的性质，轨线Γ1与充分接近，且在两轨线都没有与脉冲集相交之前，它们没有交点。又由于点是全局稳定的焦点，所以经过C′的轨线肯定与脉冲集M相交，设其交点为，则其坐标可设为(h，)，显然＜yB1，且充分接近B，根据系统(2)可得＜。从而C的后继函数g(C)=＜yC1＜0。同样取集合N1与x轴交点D′，则yD′=0。经过D′的轨线设其为，由于点是全局稳定的焦点，所以经过D′的轨线肯定与脉冲集M相交，设其交点为，则其坐标可设为(h，)，则yD′1＞0。从而点的相点为((1-p)h，(1-p))。从而的后继函数g(D′)=-yD′＞0。由后继函数的连续性1知，在线段D′C′一定存在一点E′，使得g(E′)=0，从而系统(2)存在阶1周期解。

类似可证以下结论：

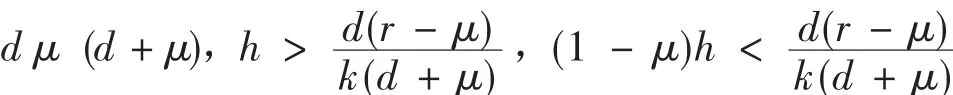
3 渐近稳定性

由上面的分析可知，系统(2)在满足一定条件下，存在阶1周期解，下面讨论阶1周期解的稳定性。

引理若乘子｜μ2｜＜1，则系统的T-周期解x＝ξ(t)，y＝η(t)是轨道渐近稳定的，其中

P(x，y)=(r－k(x＋y)-μ)x，Q(x，y)＝μx－dy，

α(x，y)=－px，β(x，y)=-py，φ(x，y)＝x－h，

(ξ(T)，η(T))=(h+η0)，(ξ(T＋)，η(T+))=

((1－p)h，(1－p)η0)，

所以

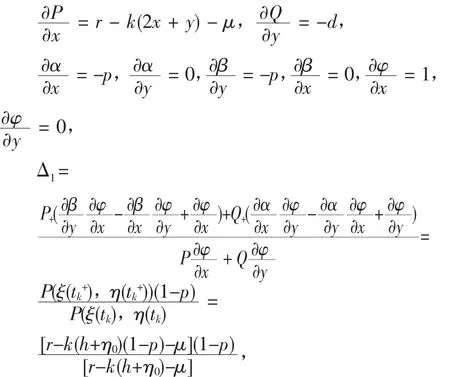
令

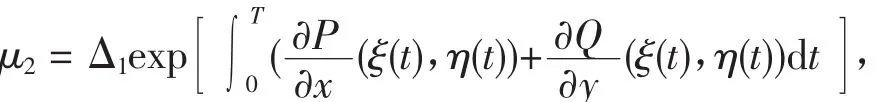
那么，对于系统(2)有因为(x(t)，y(t))是系统(2)的周期为T的周期解，则

[1]马知恩.常微分方程定性与稳定性方法[M].北京：科学出版社，2001.

[2]张知彬.鼠类不育控制的生态学基础[J].兽类学报，1995，15(3)：229-234.

[3]宛新荣，石岩生.不育剂对黑线毛足鼠种群繁殖的影响[J].兽类学报，2006，26(4)：392-297.

[4]张知彬，张健旭.不育和“灭杀”对围栏内大仓鼠种群繁殖力和数量的影响[J].动物学报，2001，47(3)：241-248.

[5]刘汉武，周立，刘伟，等.利用不育技术防治高原鼠兔的理论模型术[J].生态学杂志，2008，27(7)：1238-1243.

[6]李秋英，刘汉武，张凤琴.具有性别结构和不育控制的单种群模型[J].河北师范大学学报，2010，34(3)：263-267.

[7]刘汉武，李秋英.不育和灭杀控制下的单种群模型[J].数学的实践与认识，2009，39(15)：104-107.

[8]刘汉武，李秋英.不育控制下的单种群动态[J].运城学院学报，2009，27(2)：9-12.

[9]魏春金，陈兰荪.状态反馈脉冲控制的Leslie-Gower害虫管理数学模型[J].生物数学学报，2012，27(4)：621-628.

A S ingle Modelw ith Contraception Im pulsive State Control

LI Xiao－xia
(Department of Applied Mathematics，Yuncheng University，Yuncheng Shanxi，044000)

In this paper，a single model with c ontraception i mpulsive state control is proposed.When it reach es the critical case，the controlmeasures are taken by harvesting.The sufficient conditions for existences of order-1 periodic solution are obtained by differential equation geometry theory and themethod of successor function.The order-1 periodic solution is orbitally asymptotically stable under some conditions.

i mpulsive state；contraception；order-1 periodic solution〔责任编辑 高 海〕

1674－0874（2013）03－0016－03

O175

A

2013-03-19

运城学院科研项目[YQ-2010011]

李晓霞(1984-)，女，山西临猗人，硕士，助教，研究方向：泛函分数。