遗传算法在楔横轧多楔同步轧控制中的应用

黎汉昌

(广东安恒铁塔钢构有限公司，广东佛山 528000)

遗传算法在楔横轧多楔同步轧控制中的应用

黎汉昌

(广东安恒铁塔钢构有限公司，广东佛山 528000)

为应对目前市场上长轴加工仍然以锻造和楔横单扎为主的加工方式的缺点，基于遗传算法优化，建立了多楔耦合关系，通过多楔控制，使多楔之间的转速、力矩、压力等因素形成协同关系，满足加工精度需要。通过遗传算法优化多楔内楔入段、外楔入段、多楔展宽段、内楔精整段以及外楔精整段五个阶段的控制，避免建立复杂模型从而提高了效率节约了成本。试验结果表明，楔横轧多楔同步技术克服了锻造和楔横单扎加工方式的不足，能够很好地解决长轴加工精度控制和成本问题。

遗传算法;多楔同步;迭代优化

随着机械、交通运输以及五金工具的发展，对于超大长轴精密加工的需求与日俱增，寻找到合适的加工方法就成为当务之急。楔横轧多楔同步通过在同一模具上安装多个楔形同时轧制轧件的多个台阶，能够有效解决加工精度、成本控制等问题，是一种长轴零件的精密成形技术。然而多楔扎同步控制是一个复杂的过程，在轧制的各个阶段内楔与外楔，楔与楔之间的制约因素难以把握，从而导致加工难度增加，此外工艺设计与模具的优化更加复杂，最终导致工艺控制难度进一步增大。当前的多楔同步是通过仿真对各楔设置固定的参数，没有形成多楔协调控制，因此采用优化方法使楔与楔之间形成协同动态控制，是一种能够有效优化控制的途径。遗传算法通过模拟自然进化过程中最优解方法，将遗传、突变、自然选择以及杂交过程引入多楔控制就成为一种可供选择的优化方法。

1 多楔同步运行和遗传算法

a．多楔同步。

多楔同步是由多个单楔构成的楔横轧方法。图1所示为一多楔同步轧制模具展开图以及轧件，中间为主楔，两侧为侧楔，对称分布，其中α为展宽角，β为成形角，θ为内楔与外楔的相对转角，由此形成了一个楔横轧多楔同步。

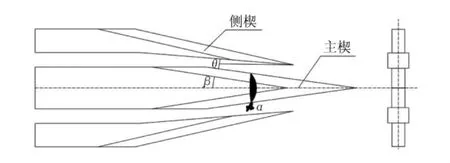
图1 多楔同步轧制模具展开图

在内楔和外楔的压力作用下，生产相继进入内楔入段、外楔入段、多楔展宽段、内楔精整段以及外楔精整段等5个主要阶段。在入楔阶段，起始部分的轧件材料能被旋转起来并能够扎出V形的深沟，随着轧制的进行，轧制的材料在楔形模的压力下形成宽度和深度一致的V形深沟;然后进入主要变形阶段，即展宽段，此时楔形模使V形沟槽逐渐扩展，使制件形状发生重大变化［1］;最后进入提高轧件尺寸精度和外观质量的精整段，楔形模对轧件进行整形，在这个过程中轧件的精确度形成是通过轧件在外力作用下轴向延生和径向延生来实现的。多楔同步扎不仅减小了轧辊辊身直径、减轻了设备质量，还提高了设备加工能力。此外多楔同步一个轧制过程能完成所有轧制要求，不需要重复轧制，降低了重复轧制的成本。由于内楔和外楔是同时轧制，所以多楔同步能进行大批量生产，并大大提高精准度。

b．遗传算法。

遗传算法是可以优化机械运行的一种方法。遗传算法出现于20世纪70年代初，是一种借鉴生物界自然选择和自然遗传机制的产物，也被称为随机和自适应搜索算法。它是根据生物进化的模型提出的一种优化算法，吸取自然生物系统“适者生存，优胜劣汰”的进化思想，从而能够提供一个在复杂空间中进行鲁棒搜索的方法，为解决许多传统优化方法难以解决的问题提供了新的途径［2］。该算法思想是将每个优化问题进行编码优化，并根据问题进行综合处理得出解决方案，包含迭代的最优解或次优的解决方案。自然选择学说包括以下3个方面:(1)遗传。这是生物的普遍特征，亲代把生物信息交给子代，子代总是和亲代具有相同或相似的性状。生物有了这个特征，物种才能稳定存在。(2)变异。亲代和子代之间以及子代的不同个体之间的差异，称为变异。变异是随机发生的，变异的选择和积累是生命多样性的根源。(3)生存斗争和适者生存。具有适应性变异的个体被保留下来，不具有适应性变异的个体被淘汰，通过一代代的生存环境的选择作用，性状逐渐与祖先有所不同，演变为新的物种。遗传算法将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串联群体中，按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选，使适应度高的个体被保留下来，组成新的群体，新的群体既继承了上一代的信息，又优于上一代。这样周而复始，群体中个体适应度不断提高，直到满足一定的条件。遗传算法的算法简单，可并行处理，并能得到全局最优解。

2 遗传算法在多楔同步控制中的应用

每一个楔参数都是不断变化的，因此需要选择相应的函数来表明当前楔具体状态，包含的信息有压力、转速以及轧件的金属流动情况。使用遗传算法进行矢量可测，每个矢量的故障预测的方向有很多个，因此对染色体采用整数编码方式，对所有的矢量进行编号。染色体的长度就是楔总数，每个基因对应压力、转速、金属流速度，而基因的取值正好对应需要优化的信号，这样一个染色体就是一个完整的楔的状态。在实际运行时，由于楔横轧多楔是经常变化的，而每个楔函数与多楔网络拓扑结构有关，在模具和要求发生变化时在每次楔压力参数发生变化后人工修改目标函数中相应的函数是不切实际的，因此必须开发自动形成目标函数的方法［3］。目标函数以及其中的设定参数所对应的完整的楔参数必须由计算机自动形成，以提高运算速度便于在线运用。

a．多楔同步运行函数。

标准的多楔遗传函数是为了保证遗传算法保持楔运行信息的完整性，这里把函数的条件尽量放宽，因为在条件选取中通常需要进行尝试和调试。遗传算法并不能处理具有网络或者空间的数据能力，因此需要通过编码描述成为遗传空间的软色体结构，在本文中采用二进制编码，将相关的参数用0，1来表示。多楔同步运行函数指利用状态信息来识别目标函数，因此可以表述为:

式中:s为楔的状态向量;Ij表示楔横轧第j个楔的状态(与参数一致为0，不一致为1);Ij(s)表示楔横轧第j个楔修正值(需要修正为1，不需要为0);n表示楔的个数。

表1为一个楔横轧多楔轧制工艺参数。

表1 楔横轧多楔轧制工艺参数

假设楔个数为3个，用S1，S2，S3表示;对应的5个阶段——内楔入段、外楔入段、多楔展宽段、内楔精整段以及外楔精整段分别为 A，B，C，D，E，理想情况下都是与参数一致的，因此将整个多楔控制按照楔分成3个部分，其控制系统调节控制量按照拓扑结果来决定。

b．遗传操作和初始群落的生成。

控制优化的目的是为了建立多楔之间的耦合关系，当第j个楔与设置的参数不一致的时候，即发出相应的控制信号，对楔压力、速度进行调整，并与其他楔之间的数据进行对比。

(1)初始化和选择。选择一个多楔系统(本文选择为一个3楔系统)，即选择一个串或个体的集合 bi，i=1，2，…，n。这个初始的群体也就是问题假

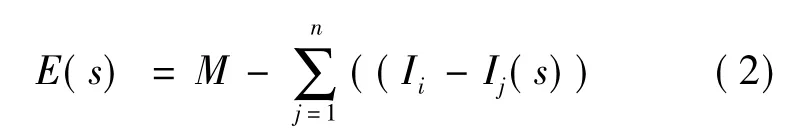
式中M表示大于总数的一个相对很大的整数。

(2)初始群体的生成。在实际运行中，为了能够准确地表明各个楔的状况，就需要进行准确的识别，在本文中采用单楔初始化。在系统中可能存在3个单点或者更多调整信号，这样选择可以大大提高搜索效率，减少搜索次数。

c．迭代操作和收敛验证。

对于选中用于繁殖下一代的个体，随机地选择两个个体的相同位置，按交叉概率P在选中的位置进行交换。这个过程反映了随机信息交换，目的在于产生新的基因组合，即产生新的个体。交叉时，可实行单点交叉或多点交叉。

全局最优收敛(Convergence to the global optimum):当最优个体的适应度达到给定的阈值，或者最优个体的适应度和群体适应度不再上升时，则算法的迭代过程收敛、算法结束;否则，用经过选择、交叉、变异所得到的新一代群体取代上一代群体，并返回到选择操作处继续循环执行［4］。全局最优收敛采用最佳保留机制，在当前群体中选择适应值最高的完全复制到下一代群落中，这样可以保证遗传算法在最后得到的结果中出现适应值最高的个体，而且能够保证所有多解保留，保证最优解都能够完整的保留［5］。在迭代初期，交叉概率非常大，遗传的概率相对小，在迭代后期操作中，遗传中的群串已经稳定，交叉作用弱化，变异的概率大大增加，将公式变化为:设解的集合。以随机方法产生串或个体的集合bi，i=1，2，…，n。问题的最优解将通过这些初始假设解进化而求出。根据适者生存原则选择下一代的个体。在选择时，以适应度为选择原则。适应度准则体现了适者生存，不适应者淘汰的自然法则。给出目标函数f，则f(bi)称为个体bi的适应度。bi为下一代个体的迭代次数。显然有:①适应度较高的个体，繁殖下一代的数目较多;②适应度较小的个体，繁殖下一代的数目较少，甚至被淘汰。

这样，就产生了对环境适应能力较强的后代。从问题求解角度来讲，就是选择出和最优解较接近的中间解。根据遗传算法的要求，将式(1)转化为最大形式:

当迭代次数到达允许的最大值，交叉概率就达到最小允许值，变异概率不能超过0.1。

3 验证及结论

利用以上方法对3楔有关协同优化问题进行仿真实验，能够获得良好的效果，在实验中种群规模N均为3，进行代数限制为50，采用单点交叉，变异区间为Lm(0.4－0.7)，按照式(2)进行实验，其遗传仿真进行控制量仿真数据见表2。

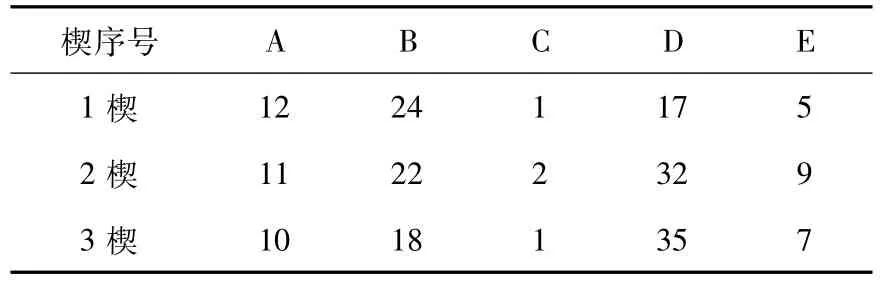
表2 多楔同步各阶段控制量仿真结果

在3楔的D控制阶段得到的测量控制量最多有35个，对比以上各阶段协同控制量来看，遗传算法能够在参数已设定的情况下根据不同的加工材料进行多楔控制，楔与5个阶段形成协同控制关系，能够很好地形成多楔控制系统。当前的多楔同步主要是通过内楔入段、外楔入段、多楔展宽段、内楔精整段以及外楔精整段等5个阶段来实现的，在这种状况下通过有限元等仿真技术对各个阶段的参数进行设置，如楔角、轴向和径向压力、轧件流速等。楔与楔之间通过仿真后以不变的参数进行轧制，这种过程表现为静态特征，因此当轧件或者轧机出现外干扰后会使得轧制过程出现扰动，甚至出现轧制失败，而且其仿真的过程极其复杂，但通过遗传算法优化这一过程，使各楔之间通过遗传优化形成一个动态的控制，那么这5个阶段就不需要每个阶段详细设置工艺参数，而是只要在最后的外楔精整阶段设置一个要求的参数即可。此外各楔之间以及内楔与外楔之间的动态关系更加有利于仿真，从而提高轧件的精准度，优化了多楔同步的控制。

［1］ 邢希东，束学道，胡正寰，等.多楔楔横轧端面移动量实时测试系统研制［J］.北京科技大学学报，2004，26(5):548 －550.

［2］ 马平，王英敏，张建.基于遗传算法优化神经网络及其在故障诊断中的应用［J/OL］.中国科技论文在线，2008(6):1－2.

［3］ Dong Yaomin，Lovell Michael，Tagavi Kaveh.Analysis of interfa－cial slip in cross － wedge rolling:an experimentally verified finite－element model.Journal of Materials Processing［R］.Beijing:Science and Technology，1998:273 －281.

［4］ Pater Z.Theoretical and experimental analysis of cross wedge rolling process［J］.International Journal of Machine Tools ＆Manufacture，2000(40):493 －495.

［5］ 王忠雷，袁文生，李兆东，等.基于STL的楔横轧模具三维建模系统［J］.山东建筑大学学报，2009，24(1):31－32.

Application of Genetic Algorithm in Control of Synchronous Process with Multi－wedge Cross－wedge Rolling

LI Hanchang
(Guangdong Anthen Iron Tower＆ Steel Structure Co.，Ltd.，Guangdong Foshan，528000，China)

Multi－wedge synchronous cross－ wedge rolling is a precise technology for processing long axial parts，can well control the machining accuracy and reduce processing cost.Based on the optimization of the genetic algorithm，it establishes a multi－wedge coupling relationship to realize multi－wedge control.These collaborative relationships include the speed，torque，pressure and other factors of the multi wedges for the processing precision requirements.It presents the genetic algorithm to optimize the control of the following five stages:multiwedge inner wedge part，outer wedge part，multi－ wedge widening part，inner wedge finishing part and outer wedge finishing part in order to avoid the establishment of complex models and reduce cost.

Genetic Algorithms;Multi－wedge Synchronization;Iterative Optimization

TH16

A

2095－509X(2013)12－0069－04

10.3969/j.issn.2095－509X.2013.12.017

2013－07－25

黎汉昌(1978—)，男，广东番禺人，广东安恒铁塔钢构有限公司工程师，主要研究方向为电力机械制造工艺。