调压系统模糊控制器的回归分析模型设计＊

卢万银

（安徽国防科技职业学院，安徽六安 237011）

调压系统模糊控制器的回归分析模型设计＊

卢万银

（安徽国防科技职业学院，安徽六安 237011）

电压调节系统常采用PID调节，其控制调节时间较长且超调量大.通过对该系统的分析，设计出满足其控制效果的模糊控制器，从而实现系统的模糊控制.考虑回归分析模型是确定的数学函数关系式，只需进行加减法与乘除法运算，在微机如PLC中有相应的指令，很容易通过编程来实现.仿真表明，其控制效果与模糊控制器控制效果吻合.

仿真；PID调节；模糊控制；回归分析

模糊控制器对比较复杂的、模型不清的系统能进行有效地控制，通过分析偏差e信号或e与其微分，划分论域，确定隶属度函数曲线，制定模糊推理规则表，模糊推理与解模糊等过程求解被控对象的输入量信号，其控制性能指标与上述所有过程密切相关.如此复杂运算过程对于采用MCS51和MCS96等微处理器的过程控制器是无法实现的，利用回归分析方法求取模糊控制器数学模型，该数学模型只需进行加、减、乘、除法运算，大大简化其应用程序的设计，从而有效地降低模糊控制系统改造升级成本，更好地推广模糊控制技术的应用.

1 系统分析

由晶闸管交流调压供电的交流位置随动系统原理如图1所示.

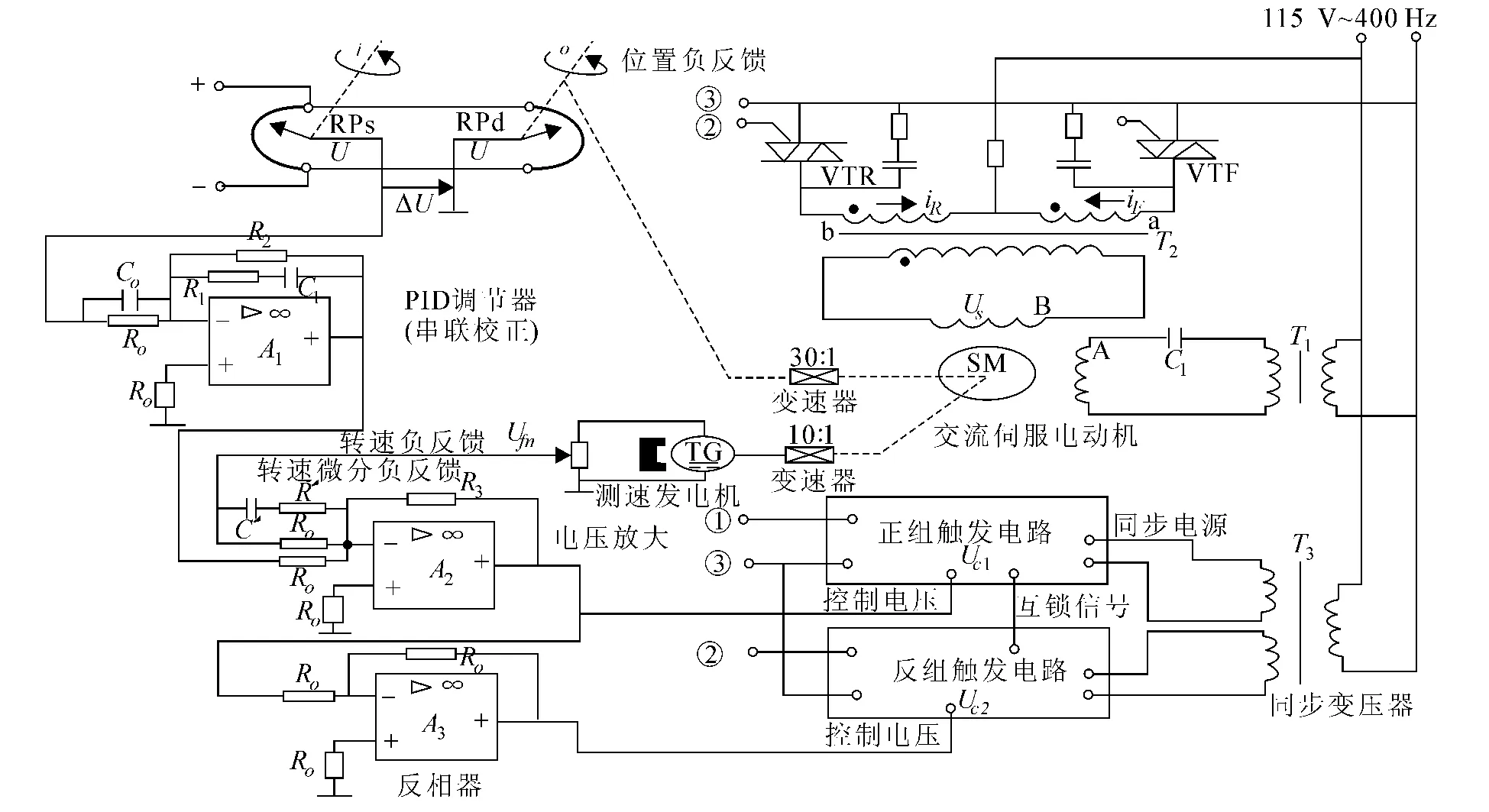
图1 调压系统原理

设系统给定量为θi，通过伺服电位器RPs转换成电压信号Uθi＝Kθi.位置随动系统的输出量为角位移θo，因此其主反馈为角位移负反馈.检测到的输出量θo通过伺服电位器RPd转换成反馈信号电压Ufo＝Kθo.由于Ufo与θi极性相反，因此为位置负反馈，其偏差电压ΔU＝K（θi－θo），该电压为控制电路的输入信号.根据系统结构的分析，构建系统模型如图2所示.

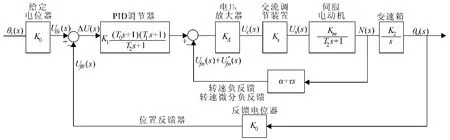
图2 系统模型

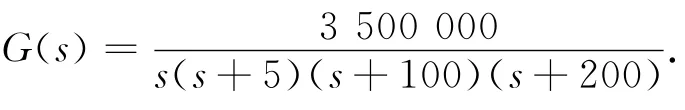
2 模糊控制器设计

2.1 控制器的论域分割

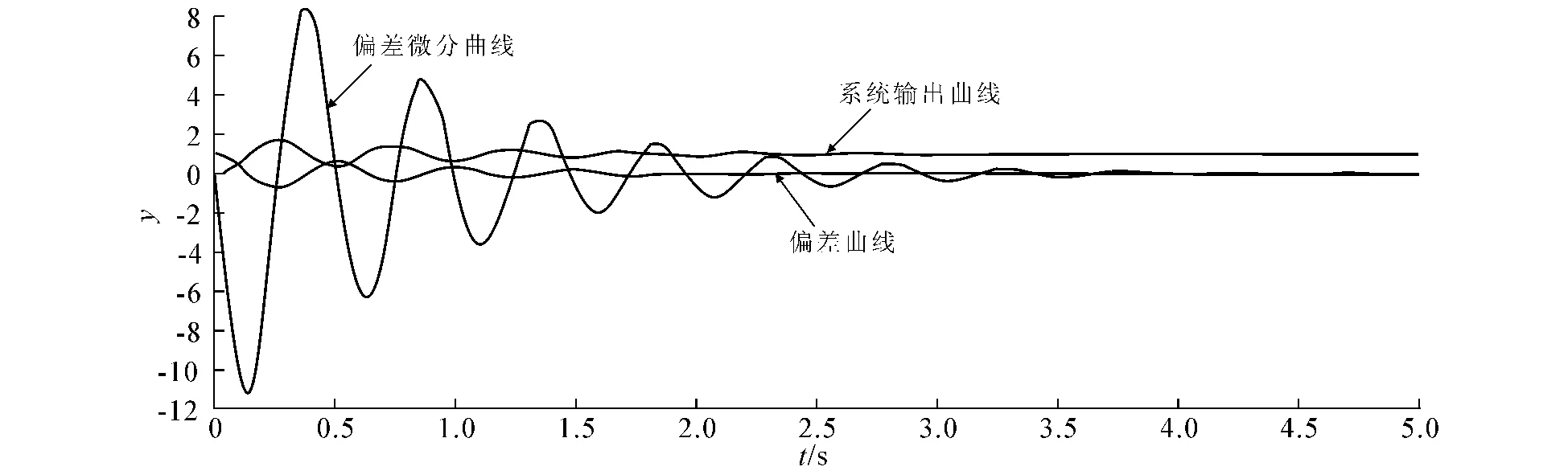
图3 偏差极其微分曲线

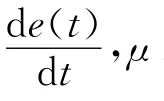
2.2 模糊规则表的建立

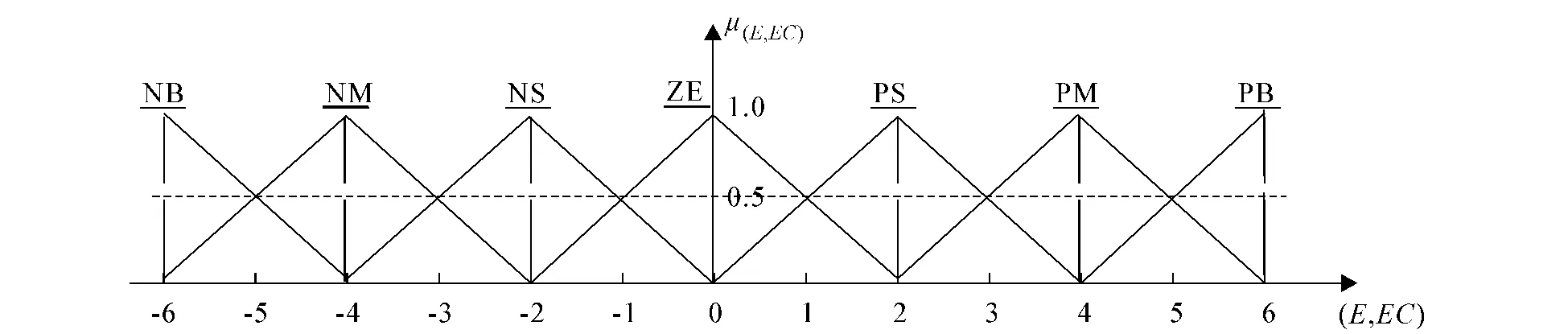
图4 隶属度函数曲线

在模糊控制器中e，de，u分别表示输入偏差、偏差微分、输出，分析图3偏差、微分及其无校正系统响应曲线，建立模糊控制规则表.在未达到调节时间前，模糊控制器的输出是不规则的曲线，当系统稳定以后，模糊控制器的输出达到稳定.

R1：IF eis PB and deis PB，then uis PB；如果偏差及其微分为正的最大，则控制器输出正的最大.此种情况一般出现在系统第1次震荡谷底时刻（见图3中0.5s左右的位置）.

……

R4：IF eis PB and deis ZE，then uis PB；如果偏差为正的最大，而其微分接近于0（如图3时刻0时位置），这时要求输出达到最大值以便快速满足系统的控制要求.

……

R24：IF eis ZE and deis ZE，then uis ZE；如果偏差及其微分为0，即系统处于稳定位置状态，这时要求输出为0，以便维持系统稳定状态的控制要求.

……

2.3 建模与仿真

为验证文中理论设计的正确性，利用Matlab的FIS（模糊推理）编辑器与Simulink相结合的方式对模糊控制器控制方法进行仿真［4］，图5给出了模糊控制器与回归分析仿真模型.

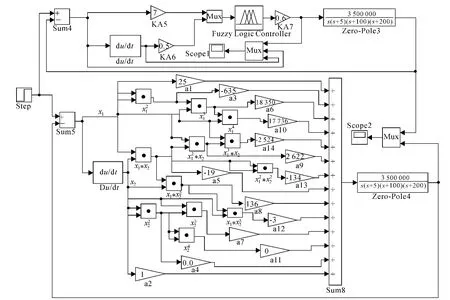
图5 模糊控制器与回归分析仿真模型

示波器2的第1个输出为模糊控制器阶跃响应仿真效果，如图6所示，模糊控制器输入与输出端的增益分别对输入与输出信号进行调节，即对模糊控制规则表进行修正，输出信号经过放大后驱动被控对象的运行.从仿真结果图6可知，模糊控制器控制在以2%的误差范围时，其调节时间在0.3s，系统无超调，稳定后无静差，模糊控制效果明显优于PID调节控制效果.

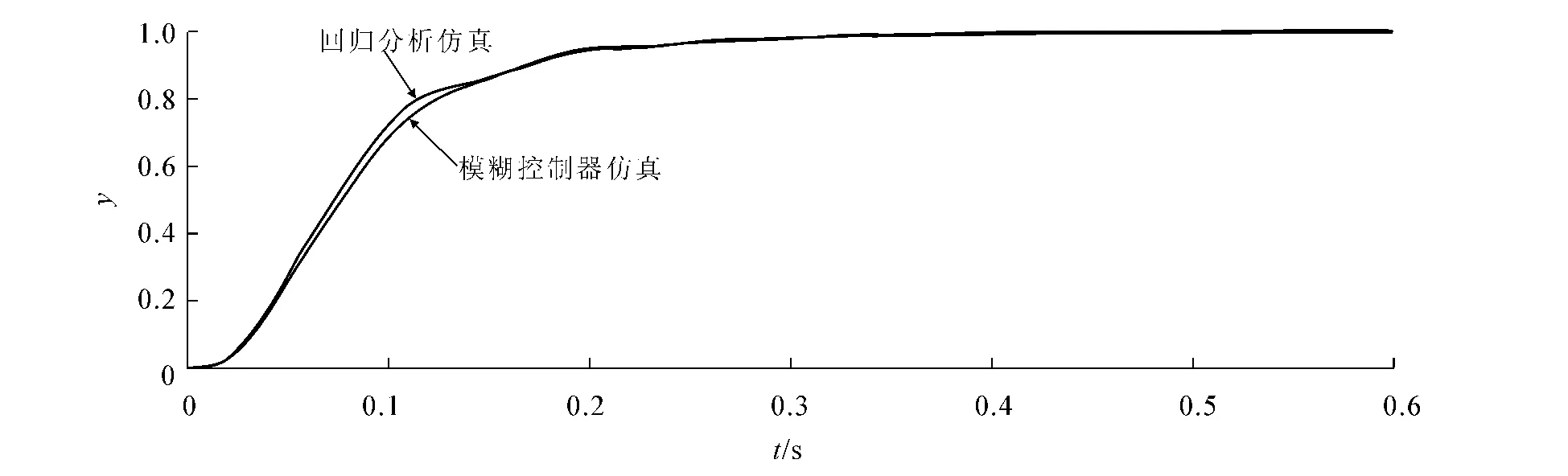
图6 模糊控制器与回归分析仿真模型阶跃响应曲线

3 回归分析模型的设计及其仿真

图5仿真模型示波器1的输出分别为模糊控制器输出、偏差输出、偏差微分输出，其仿真结果如图7所示.从图7中取出15组数据，取偏差E分别为1，0.97，0.87，0.73，0.59，0.54，0.40，0.32，0.19，0.15，0.07，0.05，0.04，0.02，0，取偏差微分DE为0，－3.99，－8.52，－9.76，－9.54，－9.37，－8.45，－7.39，－3.15，－1.72，－1.56，－0.37，－0.70，－0.19，0，则对应输出U为3.41，1.83，0，0，0，－0.19，－0.72，－1.07，－0.20，0.27，－0.35，0.17，－0.23，0.09，0.

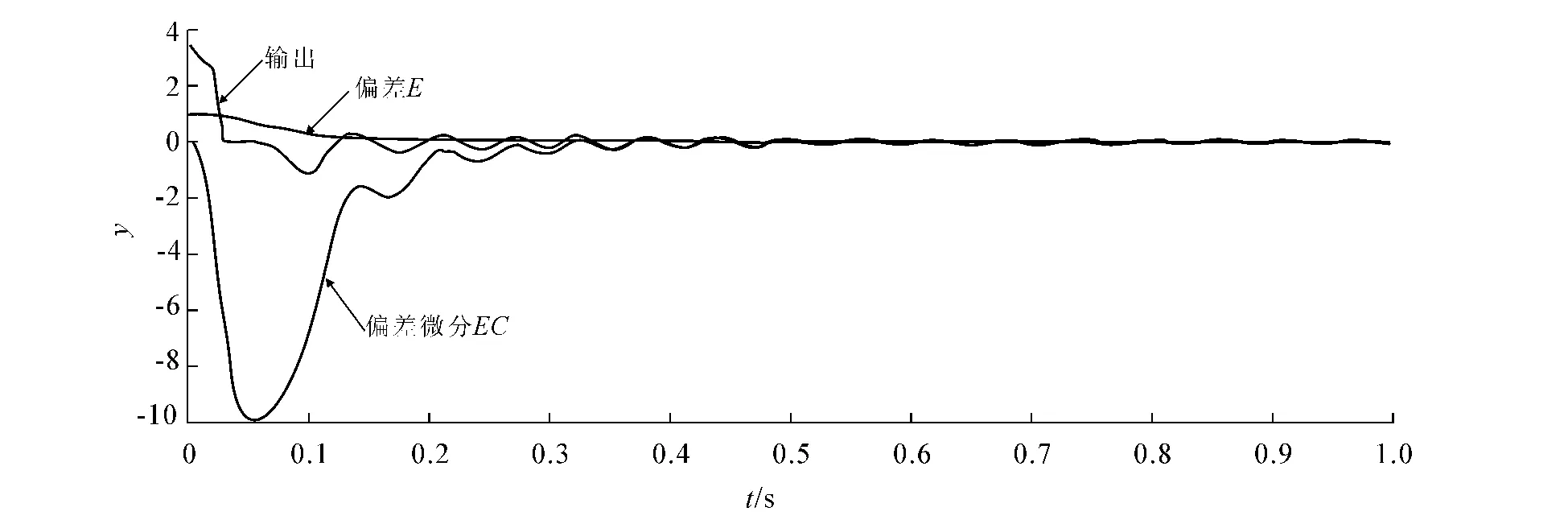
图7 模糊控制器输入输出关系曲线

3.1 回归分析方程的建立

根据上述15组数据设计线性回归方程，由于偏差E与偏差微分DE取最高项为4次方，列出15个方程，解出15个未知数，从而确定其线性回归方程.设x1＝E，x2＝DE，则方程为

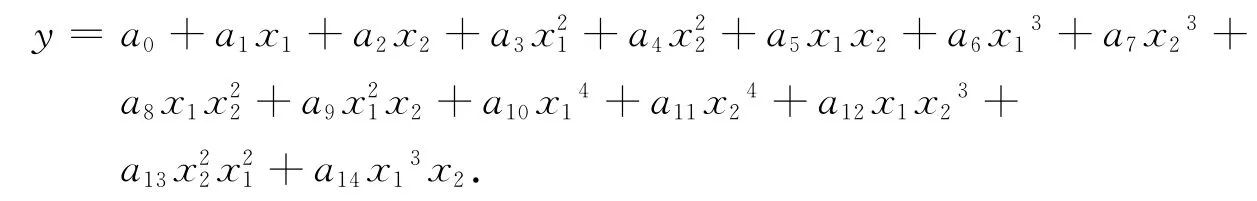
3.2 回归方程参数的确定

利用Matlab程序求出ai，i＝0，1，2，...，14，由15组x1，x2建立B15×15矩阵，已知y值，由A＝y／B求得A值即ai.运行程序得到

3.3 模型的设计与仿真

根据回归分析方程表达式建立模糊控制器的回归分析仿真模型（见图5的下部分），正弦响应仿真效果如图8所示.比较可知，模糊控制器通过回归分析辨识得到的模型与模糊控制器仿真效果吻合.

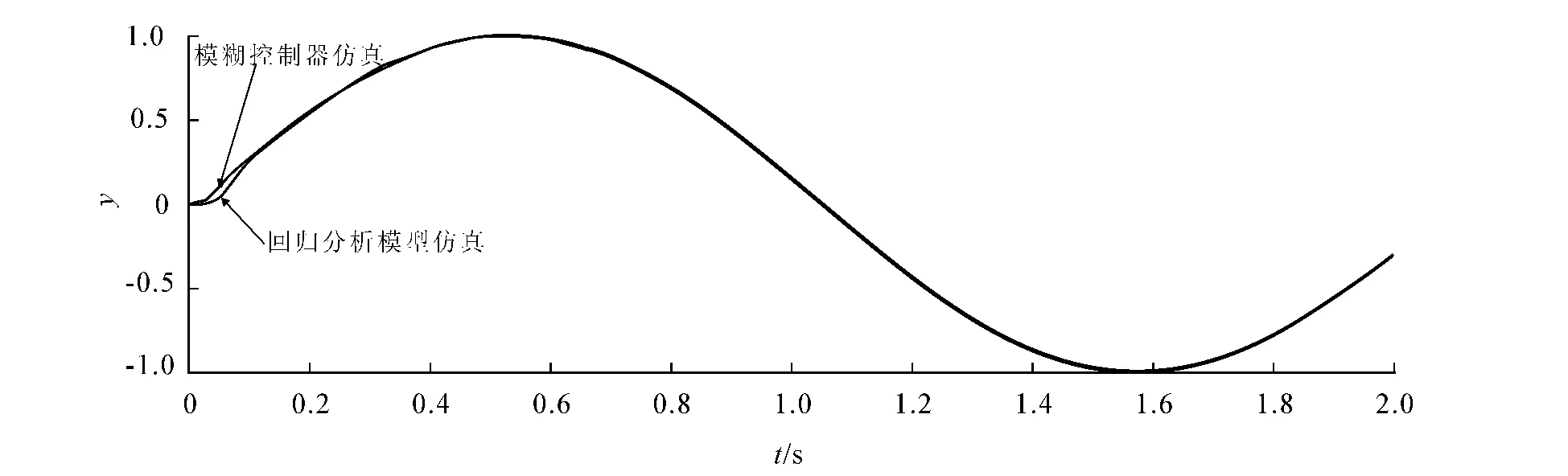
图8 模糊控制器与回归分析仿真模型正弦响应曲线

4 结语

笔者设计的模糊控制器回归分析模型只需通过简单的加、减、乘、除法运算就可求出控制信号，编程简单，容易在PLC等微机中实现，避免了模糊控制的模糊化处理、合成、规则表建立与推理等复杂运算过程.

［1］ 孔凡才.自动控制原理与系统［M］.北京：机械工业出版社，2008.

［2］ 李洪兴.模糊控制器与PID调节器的关系［J］.中国科学，29（2）：1－10.

［3］ 席爱民.模糊控制技术［M］.西安：西安电子科技大学出版社，2010.

［4］ 闻 新.MATLAB模糊逻辑工具箱的分析与应用［M］.北京：科学出版社，2001.

（责任编辑 陈炳权）

Fuzzy Controller of Voltage Regulator System Regression Analysis Model Design

LU Wan－yin
（Anhui National Defence Vocational College，Liuan 237011，Anhui China）

Voltage regulating systems often uses PID regulation which requires long time to control and has large overshoot.Based on the analysis of the system，a kind of effective fuzzy controller was designed.Since the regression analysis model is determined by the mathematical function relationship，it is enough to make addition and subtraction，multiplication and division operations，so it can easily be programmed to achieve in microcomputers such as PLC instruction.Through the simulation，the control effect of regression analysis model and fuzzy controller model is basically consistent.

simulation；PID control；fuzzy control；regression analysis

TP183

A

10.3969／j.issn.1007－2985.2013.03.011

1007－2985（2013）03－0050－05

2013－03－01

2011—2013年中央财政支持高等职业院校专业服务能力建设资助项目

卢万银（1969－），男，安徽金寨人，安徽国防科技职业学院副教授，主要从事智能控制技术研究.