一种新型非线性PI控制器的设计及其仿真＊

廖柏林

（吉首大学信息科学与工程学院，湖南吉首 416000）

一种新型非线性PI控制器的设计及其仿真＊

廖柏林

（吉首大学信息科学与工程学院，湖南吉首 416000）

针对过程控制普遍存在的大时滞、大惯性对象，设计并仿真了一种新型非线性PI控制器.该控制器的前置非周期采样单元补偿被控对象的时滞特性，非线性PI控制环节加快调节过程并减少超调量，MATLAB的S－Function实现了非周期采样和非线性环节的仿真.仿真结果表明，该新型非线性PI控制器具有较小的超调量、较短的过渡时间，在模型失配的情况下仍具有良好的控制性和鲁棒性.

非周期采样；非线性；PI控制器；仿真

工业过程控制领域中，被控对象往往具有大时滞、大惯性等特性，其大滞后特性使超调量不能及时反映控制作用的变化，当被控对象受到干扰而引起超调量改变时，控制器产生的控制作用也不能马上对干扰进行补偿.具有时滞特性的控制系统往往存在较长的调节时间和较大的超调量，其振荡使得控制系统的品质和稳定性低，甚至系统有时无法正常工作.Smith预估补偿控制器为解决时滞系统的控制问题提供了一种理论上可行的方法，但是Smith预估控制器过分依赖于补偿模型的准确性，且鲁棒性差，因而限制了它在实际过程控制中的应用［1］.

常规PID（Proportional－Integral－Derivative）控制器结构简单，其比例、积分、微分3项具有明确的物理意义，是一种应用十分广泛且比较成熟的控制器.目前，全球工业过程控制中所用控制器80%以上仍采用传统PID控制器，如果包含各种改进型，则超过90%［2－3］.近些年来，对具有大时滞和大惯性特性的这一类被控对象，一些研究者尝试通过改造传统PID控制算法来提高系统的控制性能［4－9］，但是仍然存在以下一些问题：（1）控制器的构造复杂，工业现场实施困难；（2）控制器严重依赖被控对象的精确数学模型，鲁棒性较差；（3）控制器参数整定繁琐［4－6］.

笔者设计前置非周期采样单元来补偿被控对象的时滞特性，利用非线性PI控制环节来加快调节过程并防止超调量过大，并对典型一阶惯性加滞后的被控对象进行仿真，仿真结果证实了文中设计的新型非线性PI控制器的有效性和优越性.

1 新型非线性PI控制器的设计原理

利用常规PID控制器对大时滞被控对象进行控制时，控制器的控制作用往往需要推迟一段时间才能在系统输出中体现出来.这使得控制器在较长的时间内只能依据一段时间前调节的结果进行控制，这显然具有很大的盲目性和多余性，控制器输入了许多无用甚至对控制不利的信息.为了使系统稳定，控制能力必然要减弱，进而导致过渡时间长和超调量增大，甚至使得控制系统根本无法工作，前置非周期采样环节可以非常好地补偿时滞问题［7］.

前置非周期采样的基本策略可以概括为：当控制系统的控制偏差大或有变大趋势，用非线性PI控制规律进行控制，如图1中bc段和ef段以及δ区域之外的部分；在控制系统的控制偏差小且无变大趋势时，不再用非线性PI控制规律控制，而是靠控制系统本身的惯性，使被控量逼近所设定的目标值，如图1中的ab段和de段.

非线性PI控制策略是为加快调节过程并减少超调量，将PI控制器的比例增益Kp取为偏差e的函数，根据偏差e的大小实时改变Kp，以提高控制性能［8］.

图1 被控量阶跃响应曲线

在非线性PI控制器前插入一个非周期采样单元（Aperiodic Sampling Unit，简称ASU）来实现非周期采样，而非线性PI控制器则采用非线性函数与传统PI控制器级联起来构成［9］，文中设计的新型非线性PI控制器的结构如图2所示.

图2 新型非线性PI控制器结构

2 新型非线性PI控制器的设计

2.1 非周期采样单元的实现

如图2所示，新型非线性PI控制器的设定值输入为r（t），输出为y（t），输入r（t）和输出y（t）之间的控制偏差为e（t），非周期采样单元的输出为f（t）（即非线性PI控制器的输入）.若可容忍的最大控制偏差值用δ表示，则非周期采样单元的策略可用利用“If－Then”结构的控制规则来进行描述，即

对于不同的控制对象，其δ值会有所不同，可以使用仿真或实验的方法得到.ASU在控制系统实际运行时，将会逐条查询控制规则，从而获得对应的匹配规则，以决定当前应采取的采样策略.当ASU查询到被控对象需要调节时，就将控制偏差完全传送给非线性PI控制器，而当ASU识别到被控对象不需要调节时，就送给非线性PI控制器一个零偏差值，使非线性PI控制器处于零输入状态.若非线性PI控制器的积分作用较弱，且在控制器输入为0时，此时输出的控制量也就几乎为0.加入前置ASU，使得新型非线性PI控制器的控制周期不是固定的，其随着控制偏差的变化而变化：偏差有变大趋势或偏差大时，每处理1次采样数据就改变1次输出控制量，控制周期小；偏差小且无变大趋势时，输出控制量保持，控制周期大.

2.2 非线性PI控制器的实现

连续控制系统的PI控制可以表示为

其中比例增益kp使控制器的输入和输出成比例关系，控制偏差产生后会立即产生控制作用，而当控制偏差为0时，控制作用也就为0.因此，比例控制是基于控制偏差进行调节的，且是有差调节.为了尽量减小偏差并加快调节速度，kp在初始时刻应较大.为减少超调量，在控制偏差e逐渐减小时，比例增益kp也应随之减小.积分增益ki＝kp／Ti是为了消除稳态误差而引入的，对系统控制有一定的滞后作用.

通过上面的分析，当控制偏差e的绝对值较小（即在稳态值附近）时，比例增益kp应取较小值，反之，kp应取较大值，即kp的值与控制偏差e的绝对值成正比，这样有利于加快响应速度，同时保证系统有很好的稳定性［10］.文中采用以双曲正割函数为基础，构造如下非线性函数：

其中kp1，kp2，kp3均为正实常数.当误差绝对值｜e｜从∞变化到0时，kp的值从（kp1＋kp2）变化到kp1，改变kp3的大小可调整kp变化的速率.积分增益ki采用Ziegler－Nichols法整定得出，并取为固定值.

3 仿真分析

大时滞对象的典型传输函数采用的一阶加纯滞后函数为

其中k为对象的静态增益，T为时间常数，τ为纯滞后时间.取k＝1，T＝60s，τ＝6s可得仿真对象的传递函数为

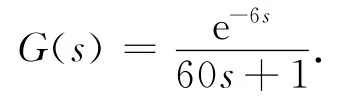
利用MATLAB进行仿真，由于非周期采样环节和非线性环节皆为复杂函数关系，Simulink库中无现成模块，而用S－Function可以方便地实现复杂的输入输出对应关系，因此，新型非线性PI控制系统仿真模型采用Simulink模块与S－Function函数相结合的形式来实现.

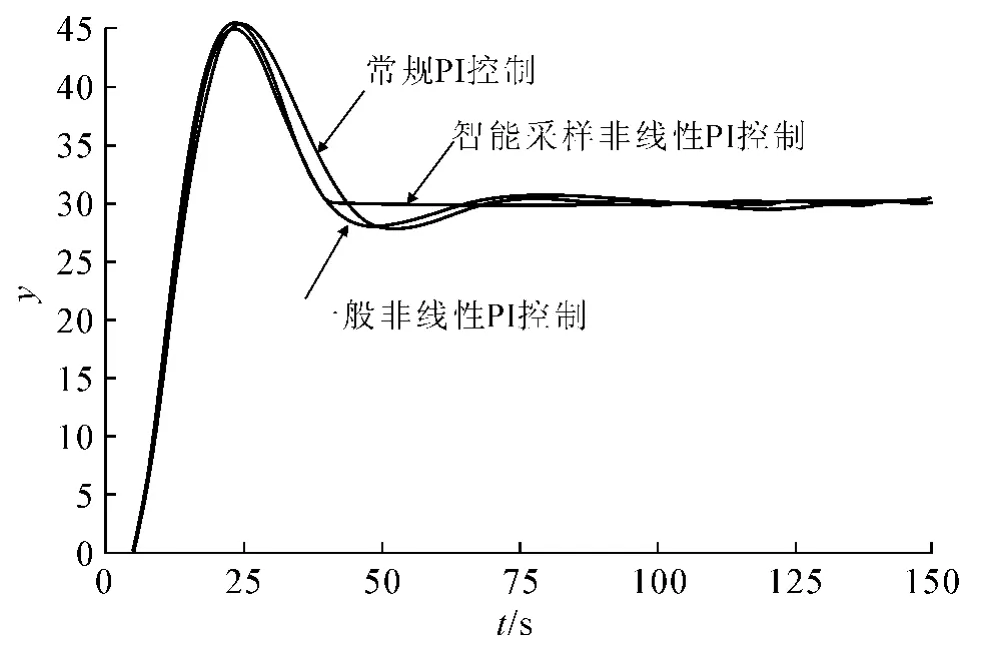
图3 智能采样非线性PI控制阶跃响应曲线

在仿真研究中，将文中新型非线性PI控制与常规PI控制及一般非线性PI控制进行了比较.其中经典PI控制的参数整定采用文献Ziegler－Nichols方法，得出PI控制器的2个参数：kp＝6，ki＝0.36.一般非线性PI控制中，kp1＝3，kp2＝3.6，kp3＝0.7，ki＝0.36.

根据仿真对象特性及工程实际，智能采样非线性PI控制中，kp1，kp2，kp3与ki仍分别取为3，3.6，0.7和0.36，系统被控量设定值为30，经仿真实验确定δ＝5.仿真结果如图3所示.

从图3可以看出，对于大时滞对象采用新型非线性PI控制器进行控制，系统的控制性能有了较大的提高.调节时间比常规PI控制及一般非线性PI控制减少了近50s，没有增加超调量，且稳态附近的波动小.这种优良的动静态控制性能得益于智能采样和非线性增益的作用，其中非线性增益kp在整个调节过程中随误差e的变化如图4所示.由图4可知，在调节过程中，当误差绝对值｜e｜大约在8以上时，非线性增益最大值kp＝6.5.随着误差绝对值变小，kp急剧变小，当达到稳态时，kp保持为3，即只有固定增益的传统PI控制器起作用.kp的这种非线性变化，既加快了系统的响应速度，又能获得较小的超调量.

为了检验智能采样非线性PI控制器的鲁棒性，将实际对象的模型参数时间常数T和滞后时间τ同时进行改变，即发生模型失配，此处实际对象的T，τ分别从60，6变为50，7，3种控制器的参数和其他条件不变，仿真结果如图5所示.从图5可以看出当模型参数发生变化时，常规PI控制器及一般非线性控制器已无法实施控制，而文中所提新型非线性PI控制器仍然可以得到比较好的控制效果，说明该控制器具有较好的鲁棒性.

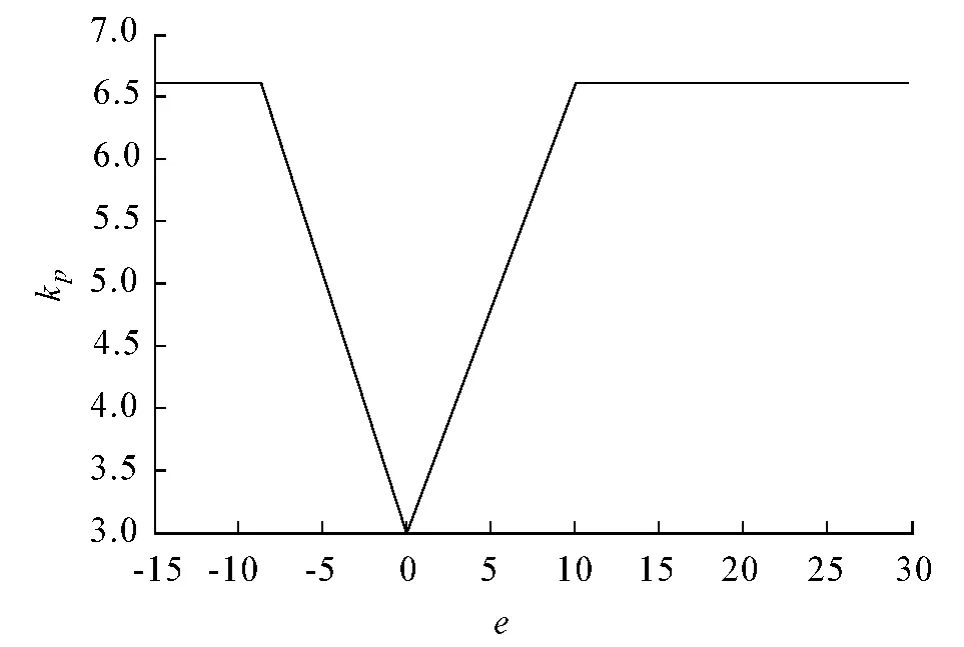
图4 非线性增益kp对误差的变化曲线

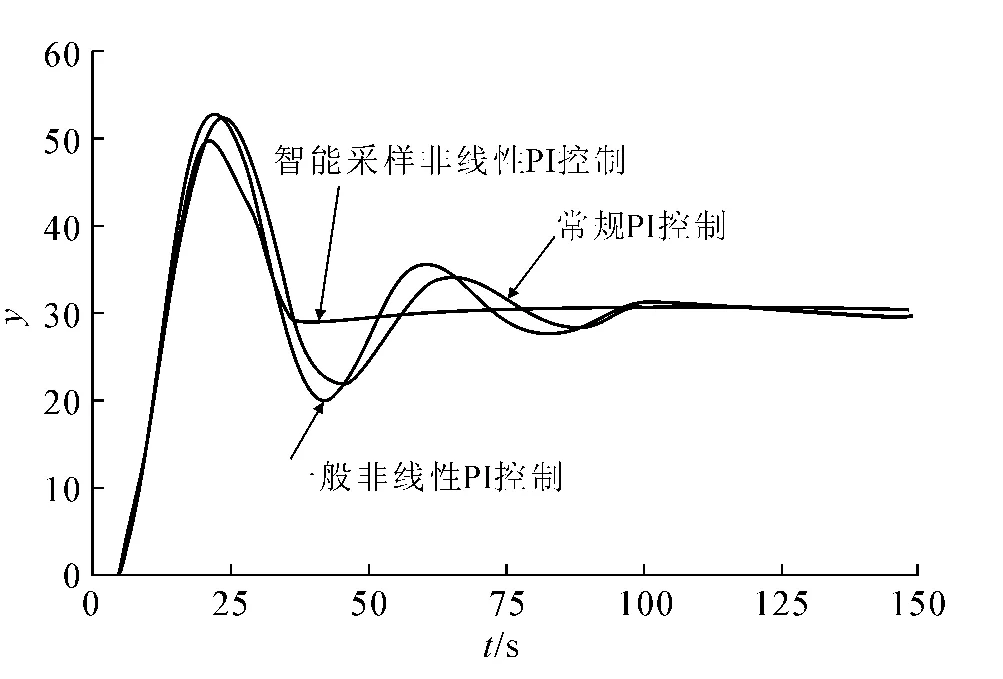
图5 模型失配时系统响应曲线

4 结语

针对具有大时滞和大惯性特性的被控对象，设计了一种新型非线性PI控制器，并给出了其设计原理和设计过程.通过将非周期采样单元ASU插入在非线性PI控制器前来补偿时滞特性，由于ASU的可调参数较少且结构简单，无需知道被控时滞对象的精确数学模型，因此对时滞特性的补偿效果较好.采用一种非线性函数来构造非线性PI控制器，其比例增益kp能跟随偏差e变化，使得控制器具有更好的动静态性能.MATLAB仿真结果表明，设计的新型非线性PI控制器具有良好的控制品质，响应时间短，稳态误差小，具有较好的鲁棒性.

［1］ ASTROM K J，HANG C C，LIM B C.A New Smith Predictor for Controlling a Process with an Integrator and Long Dead Time［J］.IEEE Trans.on Automatic Control，1994，39（2）：343－345.

［2］ 王 伟，张晶涛，柴天佑.PID参数先进整定方法综述［J］.自动化学报，2000，26（3）：347－355.

［3］ 霍延军.基于量子粒子群算法的PID参数自整定方法［J］.微电子学与计算机，2012，29（10）：194－197.

［4］ MANTAUSEK M R，MICIC A D.On the Modified Smith Predictor for Controlling a Process with an Integrator and Long Dead－Time［J］.IEEE Trans.on Automatic Control，1999，44（8）：1 603－1 606.

［5］ CHIEN I L，PENG S C，LIU J H.Simple Control Method for Integrating Processes with Long Dead Time［J］.J.of Process Control，2002，12（3）：391－404.

［6］ 李明河，王 萌，施艳艳.基于动态神经网络在线辨识的PID控制［J］.微电子学与计算机，2008，25（3）：43－46.

［7］ 胡可剑，何文光.一种纯滞后过程补偿的智能采样调节器［J］.兵工自动化，1990（3）：31－34.

［8］ 钟庆昌，谢剑英，李 辉.变参数PID控制器［J］.信息与控制，1999，28（4）：273－277.

［9］ 苏玉鑫，段宝岩.一种新型非线性PID控制器［J］.控制与决策，2003，18（1）：126－128.

［10］ 刘金琨.先进PID控制及其MATLAB仿真［M］.北京：电子工业出版社，2003：189－190.

（责任编辑 陈炳权）

Research and Simulation of a New Nonlinear PI Controller

LIAO Bo－lin

（College of Information Science and Engineering，Jishou University，Jishou 416000，Hunan China）

For the problem of large time－delay and great inertia in the process control field，a new nonlinear PI controller is proposed which can compensate the time－delay features by an aperiodic sampling unit，speed up the adjustment process and reduce the overshoot by a nonlinear PI controller.The simulation of the aperiodic sampling unit and nonlinear unit is realized by the S－Function of MATLAB.Simulation results demonstrate that the new nonlinear PI controller has less overshoot and faster response.In the case of the model－process mismatch，it also has a good performance and robust stability.

aperiodic sampling；nonlinear；PI controller；simulation

TP13

A

10.3969／j.issn.1007－2985.2013.03.010

1007－2985（2013）03－0046－04

2013－03－26

国家自然科学基金资助项目（61102089）

廖柏林（1981－），男，湖南衡阳人，吉首大学信息科学与工程学院讲师，博士生，主要从事过程控制、机械臂控制和神经网络等研究.