螺栓联接梁结构结合部非线性特性参数辨识＊

孙 伟，李星占，韩清凯

（1．东北大学机械工程与自动化学院，辽宁 沈阳 110819；2．上海交通大学机械与动力工程学院，上海 200240；3．大连理工大学机械工程学院，辽宁 大连 116023）

引 言

螺栓联接是机械结构系统最常见的联接形式，通常情况下，螺栓联接结构的结合部会对系统的动力学特性产生很大的影响。与刚性联接对照，结合部的力学特性参数会使结构的固有频率、刚度和阻尼等都会发生改变，而表现出非线性动力学特性。因此，为了有效创建螺栓联接结构系统的动力学模型以及对振动响应进行精确预测，需要辨识结合部的动力学特性参数（主要是刚度和阻尼参数）。

近年来关于结合部参数辨识的研究有很多，通常采用实验数据与有限元模型相结合，即通过最小化实验测试数据和有限元分析模型预测结果之间误差的方法来获得最合适的结合部特性参数［1～3］。但是，由于有限元方法及实验测试都存在着误差，误差的相互叠加使这种参数辨识方法很难精确辨识出结合部的力学特性参数。

鉴于这种情况，很多学者从不同的角度提出建立各种解析模型来辨识螺栓结合部特性参数的方法，例如，Ma等提出通过对比无螺栓联接和有螺栓联接的梁的动力学特性［4］，来辨识结合部的非线性参数。Ahmadian提出建立一种通用联接单元的方式来表示螺栓联接处的非线性［5］，并将这种单元引入到结构控制方程中，最后通过实验测试获得的线性固有频率、非线性频响函数来辨识结构的阻尼和刚度。Lee将非线性结构的响应表示为Volterra级数［6］，通过对高阶频响函数的分析，辨识出结构的线性和非线性参数。由于对螺栓联接结合部非线性产生机理的认识不清，上述对螺栓结合部参数辨识的研究还未得到公认，因而，围绕螺栓结合部参数辨识还需要深入开展研究。

力状态映射法（Force－state mapping）是通过在某阶固有频率附近定频激励结构，测得其激励和响应的时域信号，根据力学模型中的函数关系对非线性参数进行辨识的一种方法［7］。按照模态理论，相互耦合的多自由动力学系统均可以解耦为若干个单自由度系统，因而力状态映射法可识别对应各阶次的非线性特性参数，有着较为广泛的应用。例如，Edward等利用Force－state mapping方法识别了一些强非线性结构的非线性模型参数［8］，Hadid对Force－state mapping方法质量和等效质量的计算方法进行了分析［9］，提出一种基于线性拟合和迭代的方法来获得非线性模型中准确的等效质量。

本文以螺栓联接组合梁为例，研究采用力状态映射法识别螺栓组合梁非线性结合部特性参数的方法。在分析结合部非线性模型以及对非线性结合部动力学特性表征测试的基础上，提出采用简化的Iwan模型模拟接触面之间的非线性动力学现象，从而建立了螺栓联接组合梁非线性解析模型。进一步，提出采用力状态映射法识别螺栓组合梁结合部的动力学特性参数的方法及相应的测试流程。最后，进行了实例研究，应用所提出的方法，辨识出了所研究的螺栓组合梁结合部的刚度及阻尼特性参数。

1 螺栓结合部非线性模型及非线性表征测试

1．1 螺栓结合部非线性模型

在研究螺栓联接结构的非线性模型时，许多学者对结合部的物理机理进行了分析，并提出多种模型来表示这种物理现象。例如，Ferri利用弹簧和粘性摩擦阻尼组成的滞回系统来表示联接部结合面之间的接触问题［10］。Gaul和Segalman概括了一些可以描述联接结构的模型，如Jenkins模型、Iwan模型、LuGre模型和 Valanis模型等［11，12］，可用以描述螺栓联接结合部非线性产生机理。

其中并联Iwan模型由于物理概念清晰，便于建模得到了较为广泛的应用［13～15］。Iwan模型将螺栓结合部的力学特性视为若干弹簧ki和库伦摩擦阻尼力Ffi的组合。对于每一个子系统，当外载荷较小时，整个系统可以认为是黏着运动，随着载荷的逐渐增加，子系统开始克服库伦摩擦，逐渐蜕化为完全的滑移运动，且临界状态会出现拍击现象。因此，并联Iwan模型可以很好地模拟联接单元的接触面在外载荷作用下产生的滑移和拍击等非线性行为。

1．2 螺栓结合部非线性表征测试

用实验来描述螺栓结合部的非线性动力学行为，即螺栓结合部的非线性表征测试。图1为本文所研究的螺栓组合梁表征测试实验系统。

测试不同激振力幅下的频响函数是表征结构系统非线性特征的最有效方式之一［16］。激振力幅值由2N变换到4N时，在一阶固有频率附近螺栓组合梁的非线性FRF曲线见图2。从图2可以看出，螺栓联接结构的1阶固有频率随着激振力幅值的增加减小，表现出明显的软化效应。

结合螺柱联接梁的非线性表征实验，Iwan模型所描述的力－位移关系可进一步简化为［5］

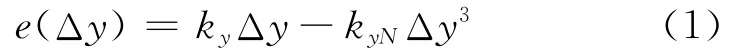
这里将线性结构中的刚度方程转化为引入库伦摩擦和滑移之后的包含立方项的刚度方程，其中e为非线性弹性力，ky和kyN分别表示线性项和立方项的刚度系数。

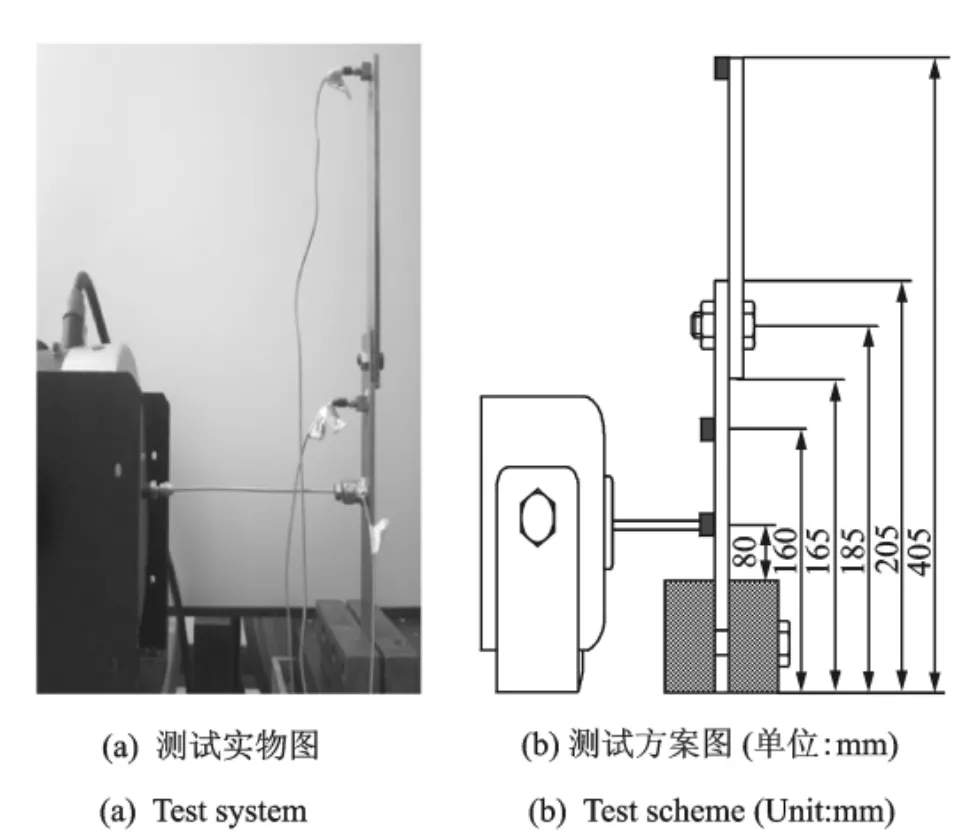
图1 螺栓组合梁非线性表征测试系统Fig．1 Nonlinear characterization test system for the bolted built－up structure

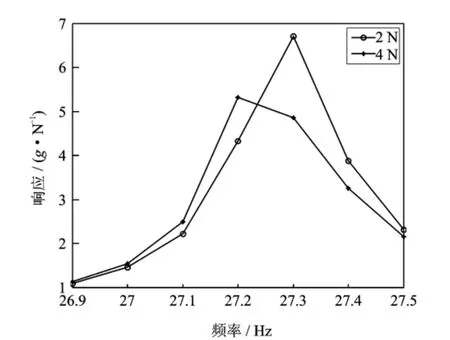
图2 不同激振力幅下螺栓联接结构的频响函数Fig．2 The frequency response function of bolted built－up structure at the different exciting levels

2 螺栓联接梁结构非线性动力学模型的建立

螺栓组合梁非线性动力学建模的思路是：首先建立起结构的线性模型，进一步采用简化的Iwan模型模拟接触面之间的非线性动力学现象，最后将非线性项引入到动力学模型中，完成螺栓组合梁的非线性动力学模型的创建。

2．1 螺栓组合梁的线性动力学模型创建

图3（a）为由两根材料及几何尺寸相同的梁通过单个螺栓联接组成螺栓联接梁结构。图3（b）为螺栓联接梁的动力学模型，联接部处包含了联接刚度及阻尼系数。

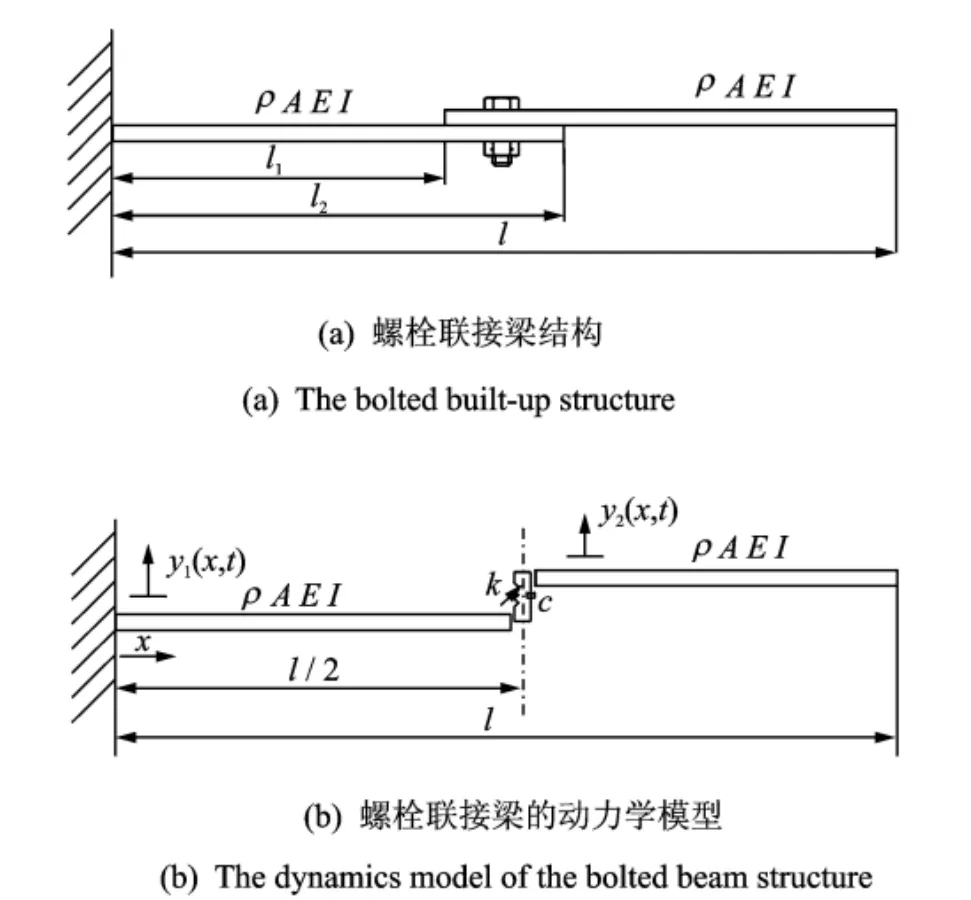
图3 螺栓联接梁结构及简化动力学模型Fig．3 The bolted beam structure and its simplified dynamics model

图3中ρ，A，E和I分别代表梁的密度、截面面积、杨氏模量和惯性矩，k和c则表示刚度及阻尼系数。y1（x，t）和y2（x，t）分别表示两个梁的横向位移。

在外界激励载荷较小时，螺栓联接结合部处不发生相对位移，可视为刚性联接。由此，按照欧拉伯努利梁理论，并引入边界条件及连续性条件，图3所示的梁结构在1阶固有频率附近的模态坐标运动方程可表示为

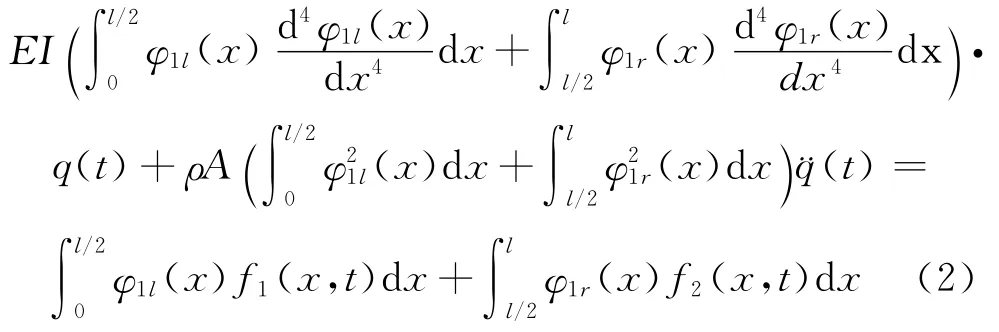
式中φ1l（x）和φ1r（x）分别表示左侧及右侧联接梁的1阶模态振型函数，q（t）为模态坐标，f1（x，t）和f2（x，t）分别是作用在两根梁的激振力。

式（2）左侧两项分别是弹性力项和惯性力项，而式（2）右侧为激振力项，由此可将方程（1）进一步表示为

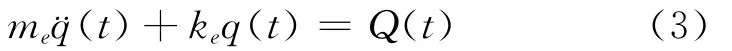
这里me为等效模态质量，ke为等效模态刚度，Q（t）为等效模态力。相应项的具体表达式为

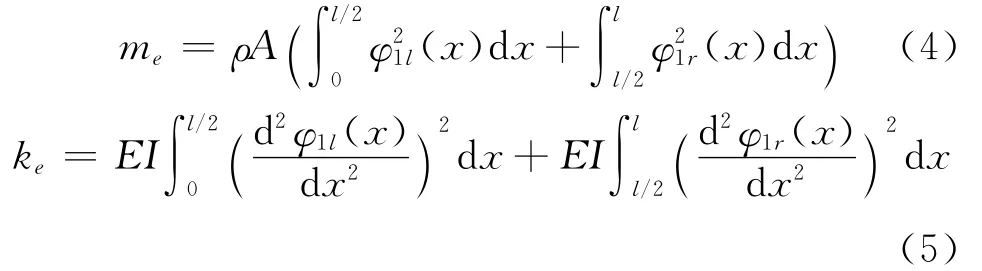
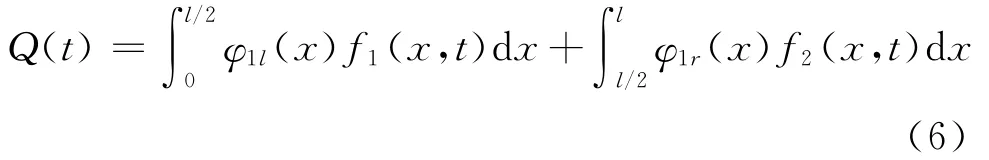
2．2 螺栓组合梁的非线性动力学模型创建

在螺栓联接结合部处，当外界载荷的幅值超过某一临界值时，联接单元的变形变大，在联接部的结合面上将产生滑移和拍击的现象。此时结合部处的刚度及阻尼效应将显现出来，且刚度值不为常数，而变成相对位移Δy的函数。相对于方程（3），此时的方程将会出现非线性弹性力项e（t）。

结合试验中观察到的软式非线性现象，并考虑结构的阻尼，按照简化的Iwan模型，最终获得螺栓联接梁在模态坐标下的非线性动力学方程为

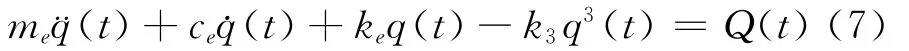
式中ce为等效阻尼，k3为立方刚度项系数。结合部的线性刚度也融入到等效刚度ke中，进一步通过正则变换，获得在正则坐标下的螺栓联接梁方程的表达为

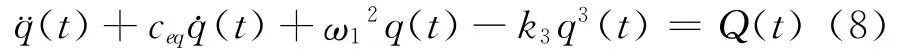
方程（8）中的k3及ceq描述了螺栓组合梁结合部的非线性刚度及阻尼参数，接下来将研究这些参数的辨识方法。

3 力状态映射法及面向组合梁的结合部动力学参数测试流程

3．1 力状态映射法及时域数据处理方法

方程（8）为典型的Duffing系统，按照力状态映射法，可变换为

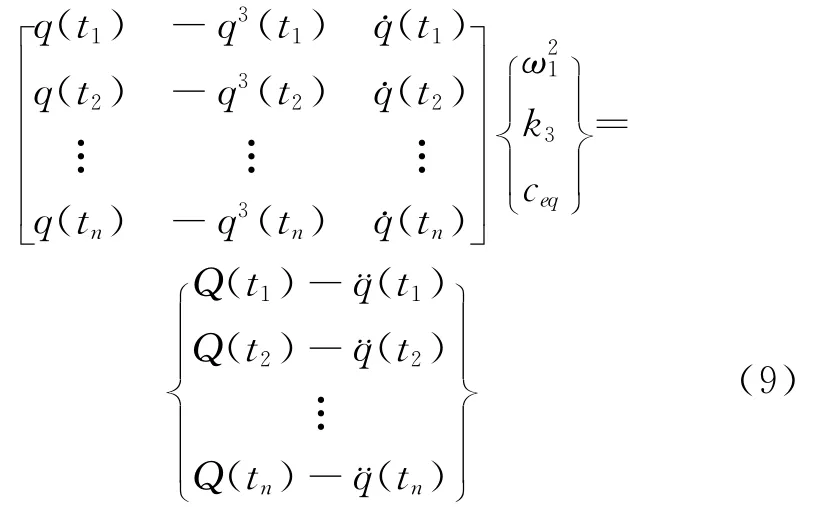
这里t1，t2，…，tn为时间序列。

进一步，可得螺栓连接结构非线性特性参数的辨识方程这里，（·）†表示伪逆矩阵。

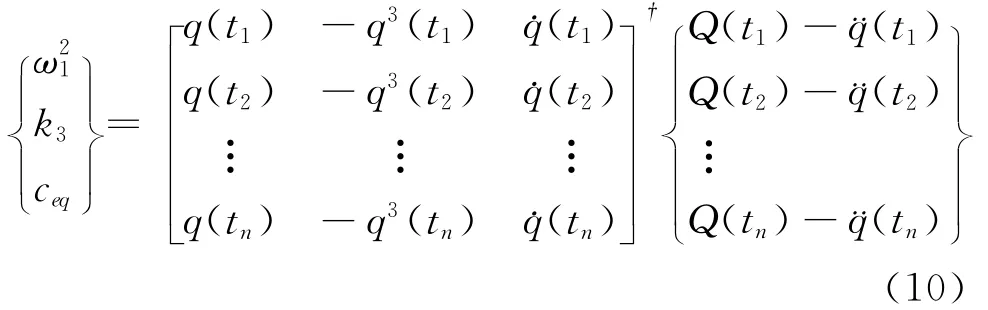
只要测得包含1阶固有频率的任一时间序列的响应信号，其他两种响应信号可通过对信号进行时域积分或微分变换来获得。记录并输入所获得的位移、速度和加速度时间序列响应信号以及激振力信号，则可辨识出螺栓联接结构结合部的非线性特性参数。

由式（10）的辨识公式可知，准确获得各种响应信号是精确辨识螺栓联接结构结合部非线性特性参数的前提。而响应信号时域微积分过程产生的误差很容易积累在最终数据上，产生辨识误差。因此，在实际测试中，首先测得的通常是加速度信号，为了减小误差，试验中采用单一频率的正弦波激励，在实际积分之前首先对测得的加速度信号做如下处理

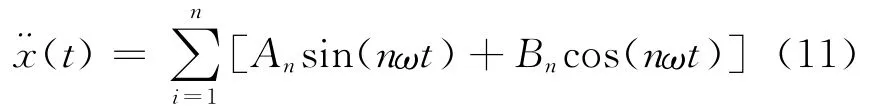
即将信号可以表示为多次谐波的叠加，通过对时域加速度信号进行各次谐波的最小二乘拟合，可以获得其中的各次系数An和Bn。这样，加速度信号就表示为解析方程的形式，然后对方程再进行解析积分就可以获得较精确的速度和位移信号，解析表达式为

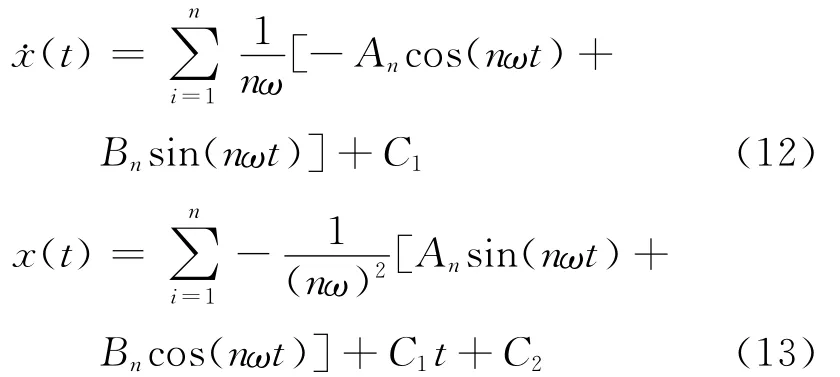
振动时，速度和位移信号的平均值为0，所以式中C1＝0，C2＝0。

这种方法通过时域信号的解析表达式进行积分，避免了数值积分方法的不稳定性和容易产生相位偏差的缺点，可以较为准确地获得所有的时域响应信号，减小了误差。

3．2 测试流程

力状态映射法测试螺栓组合梁结合部特性参数的流程可概括为以下6个关键步骤：

（1）组合梁线性固有频率测试

可采用经典的实验模态测试方法，例如，通过锤击、电磁激振器、振动台等激励设备激励组合梁，用加速度传感器拾振完成模态测试。进一步获得结构的频响函数，从频响函数中获得组合梁的固有频率值。

（2）测试包含某阶固有频率的非线性频响

测试非线性频响的目的是为了确认能够激发出结合部非线性特性的频带及激励幅值。当在某一激励幅度下，组合梁的结构的固有频率发生明显偏移，则说明组合梁结合部已表现出非线性振动特性，可记录这个频带和激励幅值。为了实现结合部特性参数的精确辨识，通常仅选取固有频率附件一小段频带（小于5Hz），另外从测试的方法上可以采用振动台或激振器进行扫频测试。

（3）定频定幅激励组合梁结构件

在所确定的频带内选择若干激励频率点（通常大于5个），用所确定的激振力幅定频激励试件，记录在每个频率下指定拾振点的响应信号和对应的激振力时域信号。

（4）时域响应信号的处理

按3．1所述的方法，对在各频率点下获得的时域信号进行变换获得与加速度信号相对应的速度及位移响应信号。

（5）模态坐标变换

所记录的激振力及位移响应信号均是用物理坐标描述的，而式（10）是用模态坐标系表示的辨识公式，为此需对时域响应信号及激振力信号进行模态坐标变换。变换公式可描述为

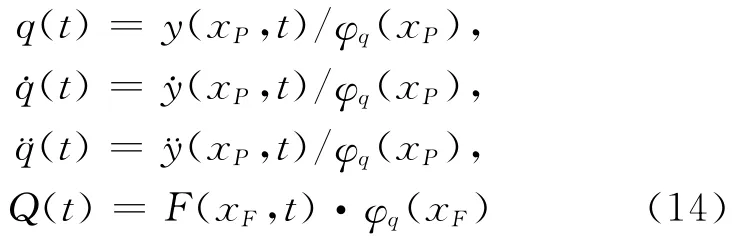
式中y（x，t），˙y（x，t），¨y（x，t）为测试获得的拾振点P处位移、速度、加速度响应信号，F（t）为激励点F处的激振力信号。φq为正则化模态振型函数，可采取有限元法或解析法，获得组合梁的正则化函数值。

（6）非线性参数识别

利用Force－state mapping方法，将某阶共振频率附近各频率点模态坐标系下的时域响应信号、激振力信号代入到式（10），可以求解出对应状态下组合梁结合部处的刚度及阻尼参数。可取平均值作为所辨识的结合部处立方刚度值，而螺栓联接结合部的阻尼通常于组合梁的振动幅值相关，即阻尼具有振幅依赖性。参照文［17］，结合部处的等效阻尼可表达为

进一步，可根据获得的等效阻尼系数和响应幅值，拟合出式（15）中的各个系数。

4 研究实例

螺栓联接梁组合结构见图1，按照3．2所述流程，利用力状态映射法辨识螺栓组合梁结合部力学特性参数。

4．1 实验测试

首先，使用力矩扳手将试件固定在夹具上，夹具上螺栓的预紧力为35N·m，联接梁上螺栓的预紧力为10N·m，实验过程中保持不变。采用随机激励扫频测试获得螺栓联接梁的线性频响函数，如图4。

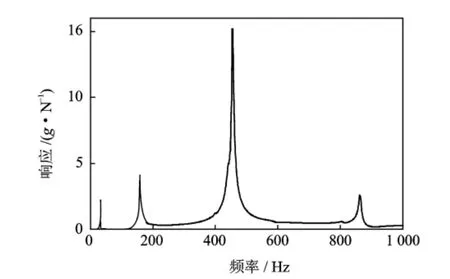
图4 螺栓联接梁的线性频响函数Fig．4 Linear FRF of the bolted beam structure

进行实验模态分析，可以获得联接梁的前四阶线性固有频率见表1。

表1 螺栓联接梁的线性固有频率Tab．1 Linear nature frequencies of the bolted beam structure

在1阶固有频率附近选取一小段频带（26．9～27．5Hz），从高频到低频进行扫频测试，不断改变激振力幅，可以发现当激振力幅大于2N时，螺栓联接结合部处出现非线性现象。随着激振力增大，非线性现象逐步明显（见图2）。

分别选取2和4N作为激振力幅，在所选频段内5个频率点进行定幅定频激励试件，记录时域加速度及激振力信号。按照式（11）至（13）对时域加速度信号进行处理，分别变换成速度及位移响应信号。图5为激振力2N，激振频率26．9Hz下的时域信号。

4．2 参数辨识

在进行力状态映射法辨识螺栓组合梁结合部特性参数前，按照测试流程，应对测试获得的物理坐标下的时域响应信号及激振力信号进行坐标变换。按照式（14），应获得组合梁的线性模态振型函数。

这里采用有限元法获得螺栓组合梁的线性模态振形函数，具体方法为：建立螺栓组合梁的有限元模型，不断修改螺栓组合梁的结合部刚度系数，直到有限元计算的固有频率与实验模态测试的固有频率相一致。最终有限元计算结果见表1，此时，输出组合梁的经正则化处理的1阶模态振型，如图6。

根据离散点的位置，可从中读取激励处和拾振点处的正则化模态振型函数值，分别为

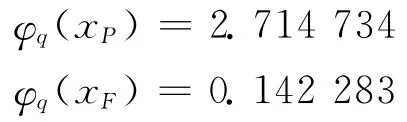
利用式（14）完成坐标变换，进一步利用力状态映射法，输入模态坐标下的时域响应信号及激振力信号，可辨识出螺栓组合梁结合部处的特性参数。表2列出了在两种激振力幅值下，结构识别出的固有频率和立方刚度项系数的平均参数值。图7为识别的不同频率点处对应这两个激励幅值的结合部等效阻尼系数。

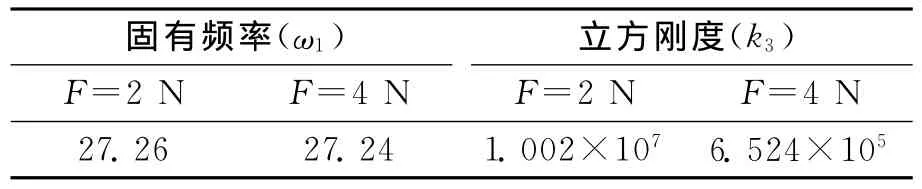
表2 螺栓联接梁固有频率及立方刚度项识别结果Tab．2 Identification results of nature frequencies and cubic stiffness for the bolted beam structure

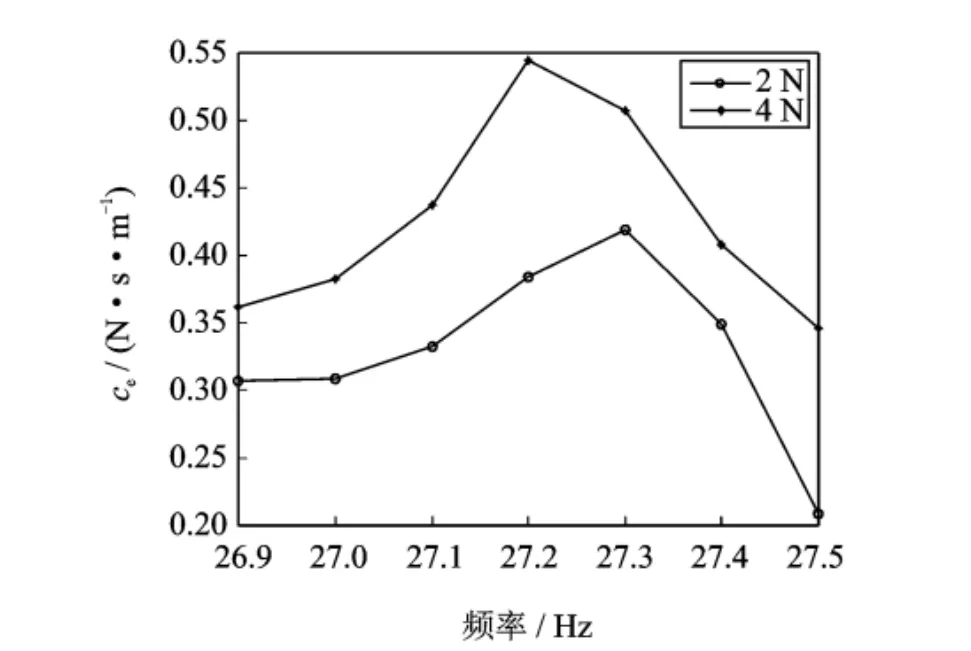
图7 不同频率对应两个激励幅值的结合部等效阻尼系数Fig．7 Equivalent damping coefficient of the joint for the different frequency at the two exciting levels

进一步，根据测得的等效阻尼系数和各频率点的响应幅值，可拟合出式（15）描述阻尼特性的二次方程系数，具体值见表3。实验数据及拟合曲线见图8和9。

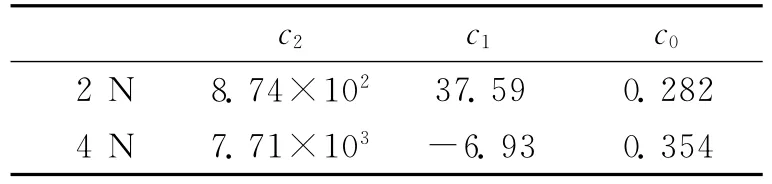
表3 螺栓组合梁结合部阻尼系数识别结果Tab．3 Identification results of damping coefficient for the joint of the bolted beam structure

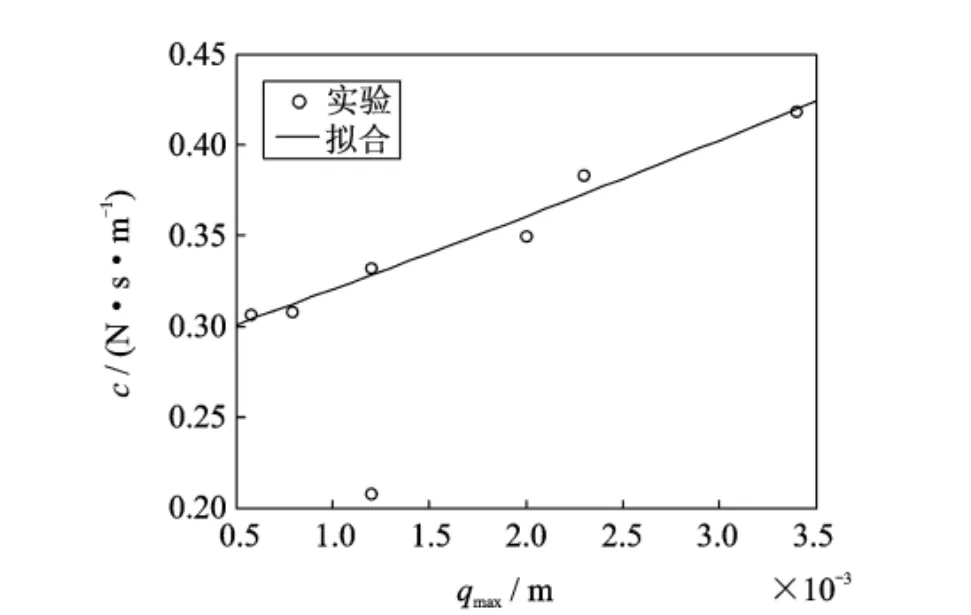
图8 2N时阻尼方程系数的拟合Fig．8 Coefficients fitting of the damping equation at 2N exciting level

5 结 论

本文研究采用力状态映射法识别螺栓组合梁非线性结合部特性参数的方法，结论包括：

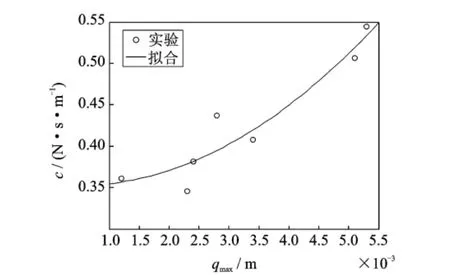
图9 4N时阻尼方程系数的拟合Fig．9 Coefficients fitting of the damping equation at 4N exciting level

（1）对所研究的螺栓组合梁表征测试，发现组合梁表现出软式非线性特性，因而可用三次立方刚度描述结构的非线性特征。

（2）采用简化的Iwan模型可以很好的模拟联接单元的接触面在外载荷作用下产生的刚度非线性行为。采用连续梁理论，并引入Iwan模型所描述的结合部非线性行为，可建立起螺栓联接组合梁非线性解析模型。

（3）对应解析模型，采用力状态映射法，具体包括：组合梁线性固有频率测试、测试包含某阶固有频率的非线性频响、定频定幅激励组合梁结构件、时域响应信号的处理、模态坐标变换、非线性参数识别等6个关键步骤，可有效辨识螺栓组合梁结合部的刚度、阻尼等动力学特性参数。

（4）辨识结果显示在同样的螺栓预紧力下，随着激振力的增加螺栓联接结构的整体阻尼会增加，表明能量耗散增加；立方刚度项系数会减小，表明结构的整体刚度减小。

［1］ LIN Y．A method of identifying interface characteristic for machine tools design［J］．Journal of Sound and Vibration，2002，255（3）：481—487．

［2］ Damjan Celic，Miha Boltezar．Identification of the dynamic properties of joints using frequency－response functions［J］．Journal of Sound and Vibration，2008，317（1－2）：158—174．

［3］ Abad J，Franco J M，Celorrio R，et al．Design of experiments and energy dissipation analysis for a contact mechanics 3Dmodel of frictional bolted lap joints［J］．Advances in Engineering Software，2012，45（1）：42—53．

［4］ MA X，BERGMAN L，VAKAKIS A．Identification of bolted joints though laser vibrometry［J］．Journal of Sound and Vibration，2001，246（3）：441—460．

［5］ Hamid Ahmadian，Hassan Jalali．Generic element formulation for modelling bolted lap joints［J］．Mechanical Systems and Signal Processing，2007，21（5）：2 318—2 334．

［6］ LEE G M．Estimation of non－linear system parameters using higher－order frequency response function［J］．Mechanical Systems and Signal Processing，1997，11（2）：219—228．

［7］ Edward F Crawley，Aubert A C．Identification of nonlinear structural elements by force－state mapping［J］．AIAA Journal，1986，24（4）：155—162．

［8］ Edward F Crawley，Kevin J O’Donnell．Force－state mapping identification of nonlinear joints［J］．AIAA JOURNAL，1987，25（7）：1 003—1 010．

［9］ AL－HADID M A．Estimation of mass and modal mass in the identification of non－linear signal and muti degree of freedom systems using the force－state mapping approach［J］．Mechanical Systems and Signal Processing，1991，6（4）：383—401．

［10］Ferri A A．Friction damping and isolation systems［J］．Journal of Mechanical Design，1995，117（8）：196—206．

［11］Gaul L，Nitsche R．The role of friction in mechanical joints［J］．Applied Mechanics Reviews，2001，52（2）：93—106．

［12］Segalman D J．Modelling joint friction in structural dynamics［J］．Structural Control Health Monitoring，2006，13（1）：430—453．

［13］Ivan I Argatov，EricA Butcher．On the Iwan models for lap－type bolted joints［J］．International Journal of Non－Linear Mechanics，2011，46（2）：347—356．

［14］Song Y，Hartwigsenb C J，McFarlanda D M，et al．Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements［J］．Journal of Sound and Vibration，2004，273（1－2）：249—276．

［15］Bograd S，Reuss P，Schmidt A，et al．Modeling the dynamics of mechanical joints［J］．Mechanical Systems and Signal Processing，2011，25（8）：2 801—2 826．

［16］Gaetan Kerschen，Keith Worden，Alexander F Vakakis，et al．Past，present and future of nonlinear system identification in structural dynamics［J］．Mechanical Systems and Signal Processing，2006，20（3）：505—592．

［17］Hartwigsen C J，Song Y，McFarland D M．Experimental study of non－linear effects in a typical shear lap joint configuration［J］．Journal of Sound and Vibration，2004，277（1－2）：327—351．