平面3－RRR柔性并联机器人动力学建模与分析＊

张清华，张宪民

（华南理工大学广东省精密装备与制造技术重点实验室，广东 广州 510640）

引 言

为了节约能源，提高工业生产率，轻型、高速、高加速度、高精度柔性并联机器人在许多领域得到广泛地应用。柔性并联机器人在诸如电子装配、精密加工与测量、航空航天领域拥有巨大的市场潜力，因此开展柔性并联机器人的研究具有十分重要的意义。

最近几十年，各国学者广泛开展了对并联机器人的研究［1］。1965年，英国高级工程师Stewart提出了一种6自由度并联机构—Stewart平台［2］，该平台后来被用于飞行模拟实验。随后出现了一大批并联机器人产品，其中最具代表性的是瑞士洛桑学院的Clavel在1988年开发的Delta机器人［1］。历经几十年的发展，刚性并联机器人的研究已取得了大量成果。然而柔性并联机器人作为一种新型的、刚－柔混联的机构，多刚体动力学的研究方法已不再适用，建立和求解柔性并联机器人的动力学模型是非常具有挑战性的工作。

近年来，一些国内外学者在柔性并联机器人的动力学方面做了一些探索。胡俊峰、张宪民研究了一种新型两自由度高速并联机械手的弹性动力学特性［3］，采用简化 KED（Kineto－Elastodynamic Analysis）方法建立了系统的动力学模型［4］。张宪民、刘济科、沈允文等对连杆机构的弹性动力学建模方法进行了探索［5，6］，考虑刚体运动和弹性运动的耦合和剪切变形的影响，并具体分析了一款六杆机构。杜兆才，余跃庆等对平面3－RRR柔性并联机器人进行了分析［7］，采用KED方法建立其动力学模型，该模型没有考虑刚体运动和弹性运动的耦合，对系统约束方程考虑不够完全。刘增善在其博士论文中系统地研究了空间3－RRS柔性并联机器人［8］，用简化KED方法建立了柔性3－RRS并联机器人动力学模型，并对动力学特性进行了分析。多伦多大学机械与工业工程学院的非线性控制实验室长期以来致力于并联机器人的研究，其中 Wang Xiaoyun，Mills Jeams K等对平面3－PRR柔性并联机器人进行了系统地研究［9～12］，并取得了丰硕的成果。Shabana A A系统地阐述了刚－柔混联机械系统的动力学建模方法［13］。张策、黄永强等详细讨论了弹性连杆机构的建模和优化设计问题［4］。

目前，国际上有关并联机器人弹性动力学建模的研究尚处于起步阶段，相关的理论还很不成熟。已有的研究结果也存在模型过于复杂难以求解、或未对模型作详尽分析，不利于理解并联机器人的动力学本质特性，也难以在实际应用中提出可有效改善其动态性能的具体策略或方法。

本文对平面3－RRR柔性并联机器人的弹性动力学问题进行了研究，采用有限元法和Lagrange方程建立了系统刚－弹耦合非线性弹性动力学模型。在求解模型时，忽略弹性变形运动对刚体运动的影响，分析了平面3－RRR柔性并联机器人动平台中心的弹性位移、弹性转角以及柔性杆件所承受的最大应力随机器人位型的变化关系。

1 机器人结构

平面3－RRR柔性并联机器人示意图如图1所示：系统由动平台C1C2C3、静平台A1A2A3、3条连接动平台和静平台的柔性支链A1B1C1，A2B2C2和A3B3C3组成，且3条支链是完全一致的，即A1B1＝A2B2＝A3B3，B1C1＝B2C2＝B3C3，主动杆与从动杆、从动杆与动平台之间用转动关节连接，连杆A1B1，B1C1，A2B2，B2C2，A3B3和B3C3都是柔性杆件，A1，A2和A3是驱动关节，B1，C1，B2，C2，B3和C3是被动关节，O为正三角形静平台A1A2A3的中心，P为正三角动平台C1C2C3的中心，O－XY为全局固 定 坐 标 系，α1，β1，α2，β2，α3，β3分 别 为 连 杆A1B1，B1C1，A2B2，B2C2，A3B3，B3C3与X轴正方向所成的夹角，θ为正三角形C1C2C3的边C1C2与X轴正方向所成的夹角。

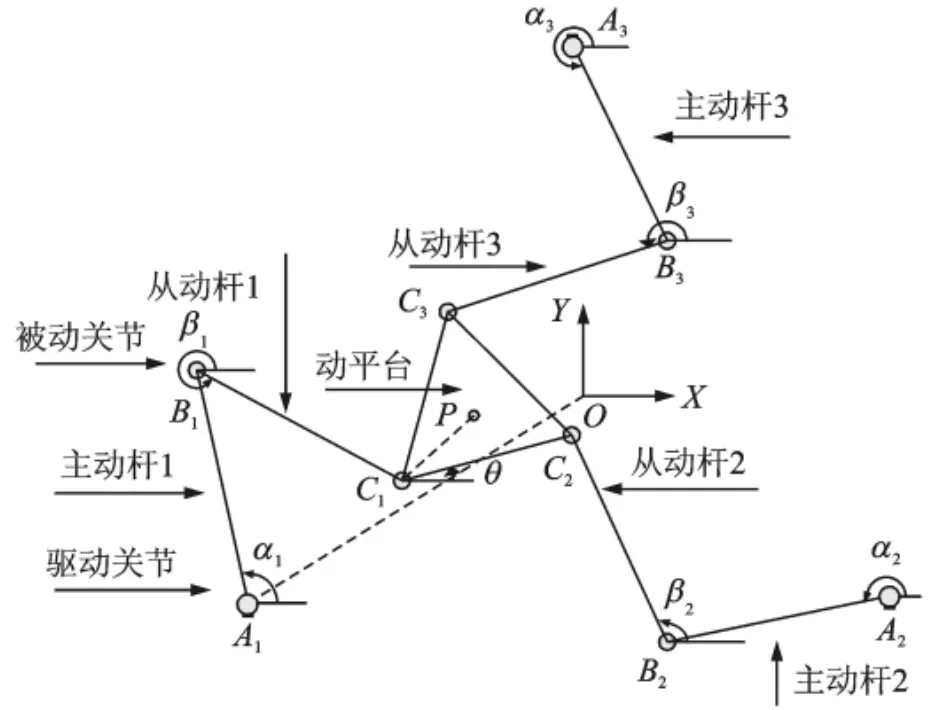
图1 并联机器人示意图Fig．1 Diagram of the parallel robot

2 单元动力学方程

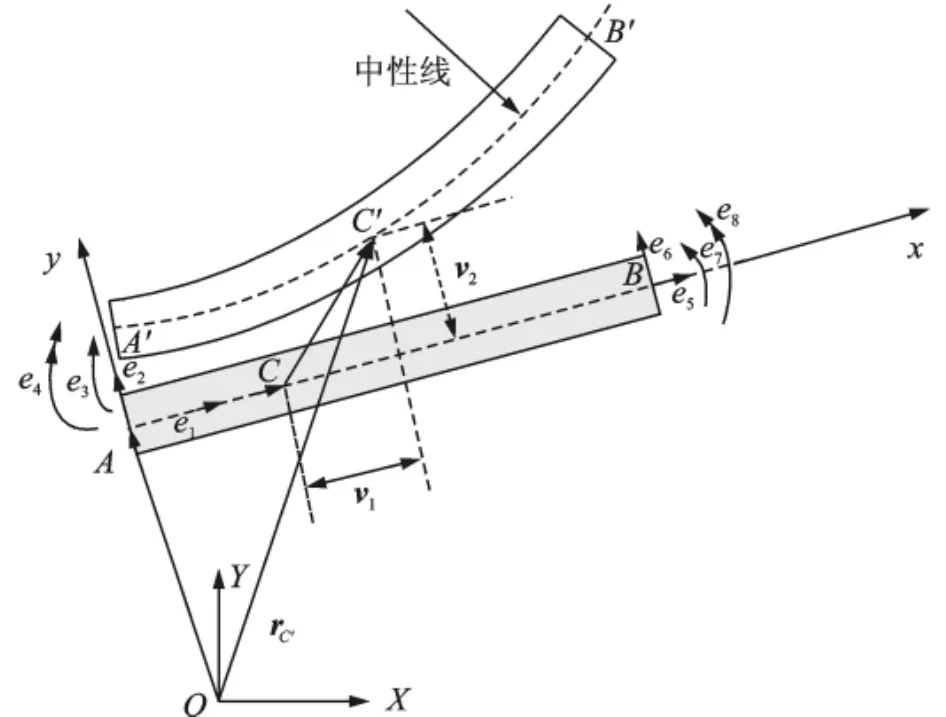
图2 单元动力学模型Fig．2 Dynamic model of beam element

将支链中的柔性连杆视为由梁单元组成，梁单元如图2所示，O－XY为全局固定坐标系，A－xy为固连于单元端点A处的局部坐标系，且x轴沿着未变形梁单元的中性线。A，B为单元的两个端点，C为单元中轴线上的任意一点，经弹性变形后到达C′处，假设单元两端点在局部坐标系中的广义弹性坐标用向量ef＝［e1，e2，e3，e4，e5，e6，e7，e8］T表示，式中e1，e5为端点A，B的轴向变形位移，e2，e6为其横向变形位移，e3，e7为其弹性转角，e4，e8为两端点处的曲率。那么点C′在局部坐标系下的位移可以表示为

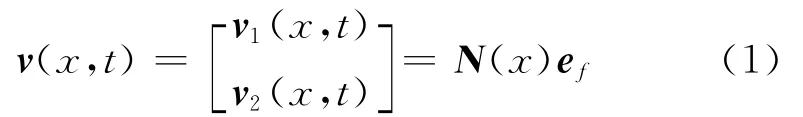
式中N（x）表示型函数。

由图2可知，点C′在固定坐标系O－XY中的位移为

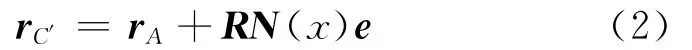
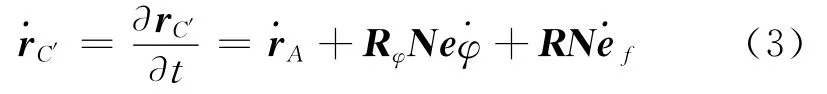
在使用Lagrange方程导出单元动力学方程之前，首先计算单元的动能和弹性应变能。

2．1 单元动能

1）平动动能

在求得单元上任意一点相对于固定坐标系的速度后，单元的平动动能可以表示为

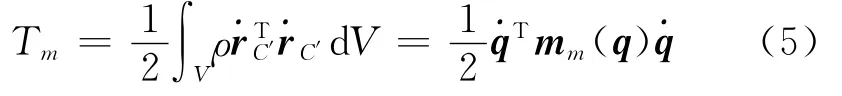
式中mm（q）为广义坐标向量q的函数。

2）梁单元截面转动动能［4］

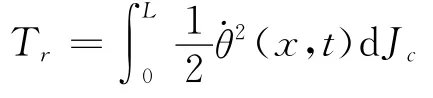
式中θ（x，t）是宽为dx的微段在真实运动中的绝对转角，dJc＝ρIdx是微段dx绕其自身质心的转动惯量，且

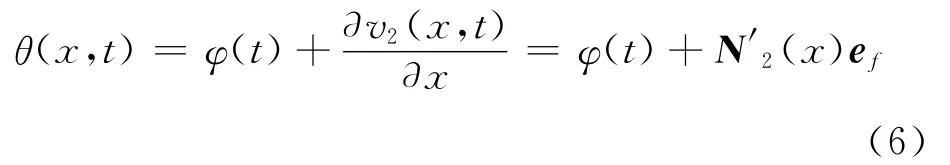
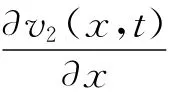
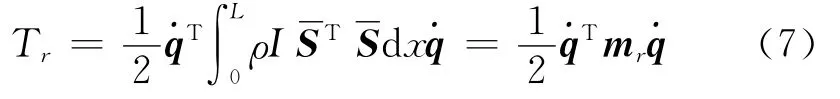
假设单元两端点处的集中质量分别为mA，mB；集中转动惯量分别为JA，JB。

3）集中质量的平动动能［4］

集中质量的平动动能可按如下方法计算：

则单元端点集中质量的平动动能为

4）集中质量转动动能［4］

类似于梁单元截面转动动能，可求得集中质量的转动动能为

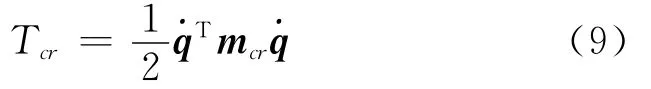
因此总的动能

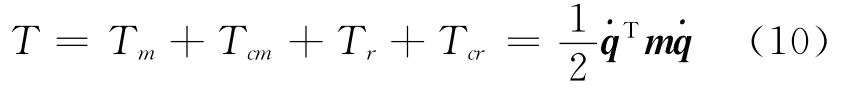
式中m＝mm＋mcm＋mr＋mcr。

2．2 单元应变能

忽略剪切和屈曲应变能，根据材料力学，单元应变能可以表示为

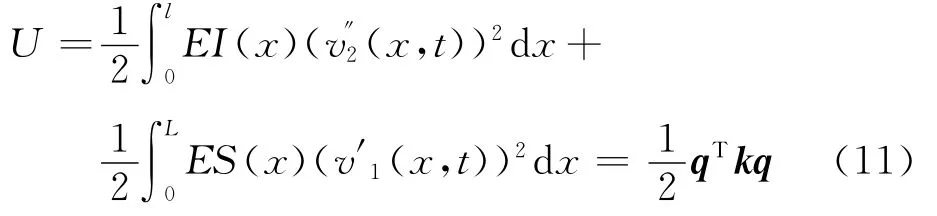
2．3 单元动力学方程

根据拉格朗日方程，可以导出单元的动力学方程

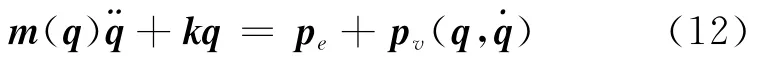
式中pe为单元所受广义外力，pv为单元的的二次速度向量，包括运动单元的科氏力和离心力且是广义坐标q和˙q的函数。

利用虚功原理可以导出单元的广义外力，设F为作用在单元上任意一点C′处的外力或外力矩，那么在外力F作用下的虚功可以表示为

根据式（2）有

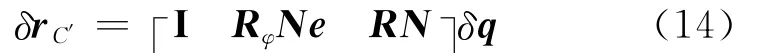
把式（14）代入式（13）得

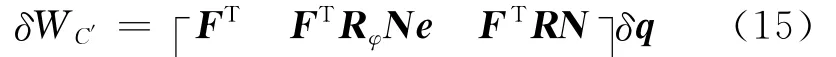
又有

比较式（15）和（16），可得点C′处的广义外力为

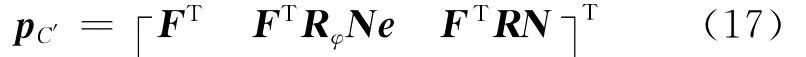
因此整个单元的广义外力为

为了形成系统动力学方程，必须把在局部坐标系下描述的单元动力学方程转移到固定坐标系上来。首先，定义8×8阶的固定坐标系到局部坐标系的转移矩阵B，则

式中Ef为单元在固定坐标系下的广义坐标向量。

式（19）对时间t求1和2阶导数

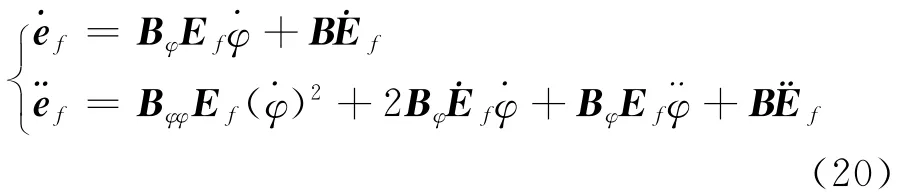
把式（19）和（20）代入式（12），并左乘矩阵

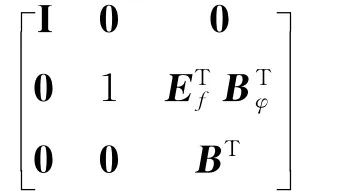
可得

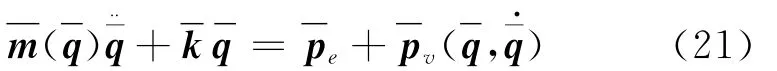
3 约束方程

分析平面3－RRR柔性并联机器人，动平台在XY平面内自由运动。3条柔性支链通过刚性动平台相连，使得各支链的弹性位移存在非线性耦合关系。因为系统是完全对称的，仅对其中一条支链Ai－Bi－Ci－P进行分析。如图 3 所示，L1，L2，L3，L4分别为向量AiBi，BiCi，CiP，OAi的长度。

3．1 刚体运动约束

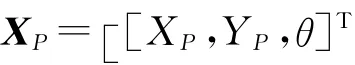
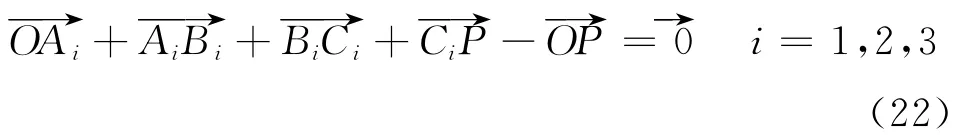
把式（22）写成沿X，Y轴的分量形式，可得如下6个约束方程

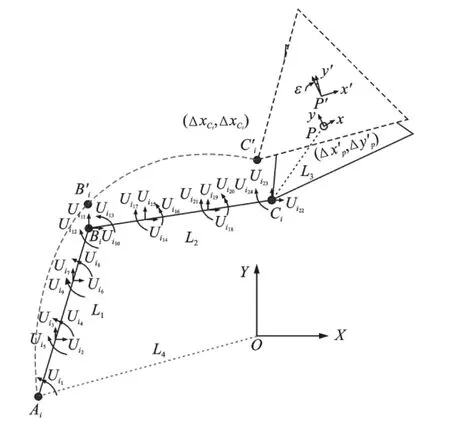
图3 支链Fig．3 The kinematic chain

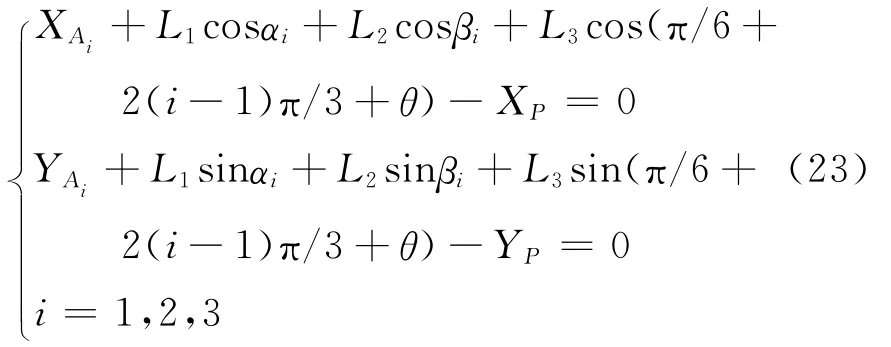
式中XAi，YAi分别表示点Ai在固定坐标系O－XY中沿X，Y轴的坐标分量。

3．2 弹性坐标约束

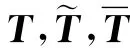
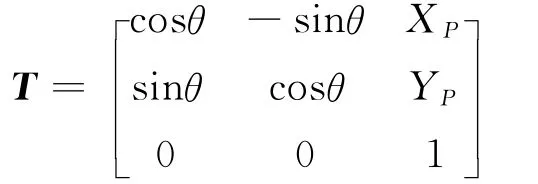
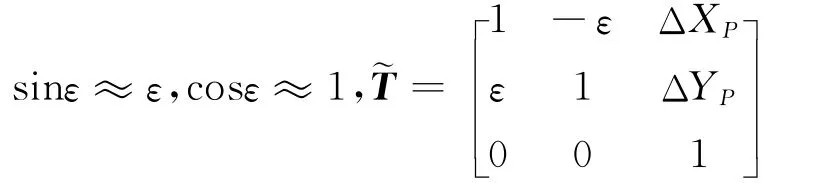
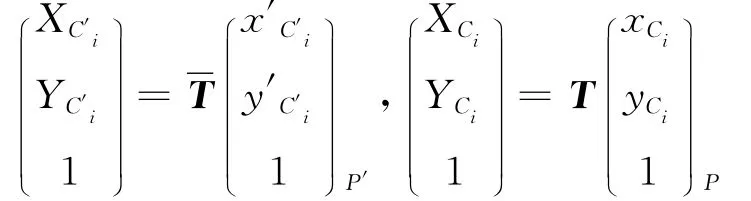
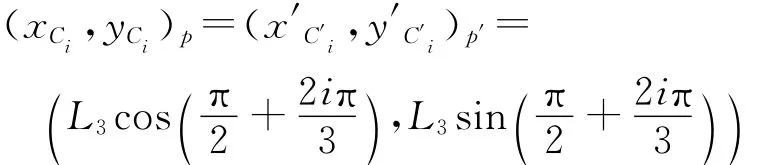
可得

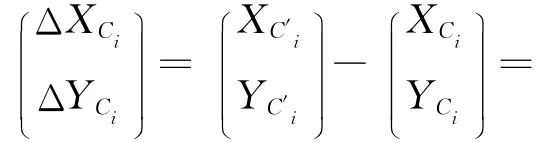
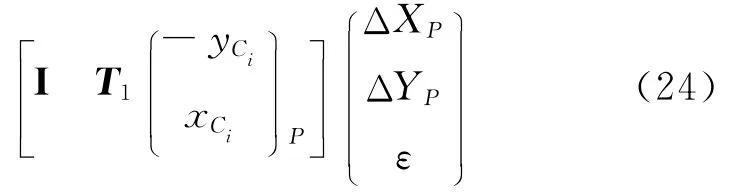
式中 I表示2阶单位矩阵。

同时动平台弹性转角与动平台相连的柔性杆末端点的弹性转角有如下的关系

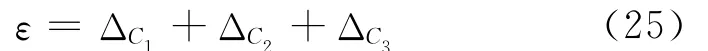
4 系统动力学方程

设U是系统的广义坐标向量，考虑约束方程式（23）～（25），组装单元动力学方程式（21），可得系统动力学方程为

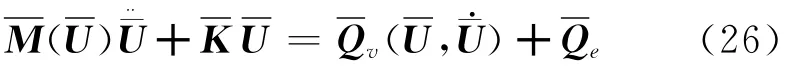
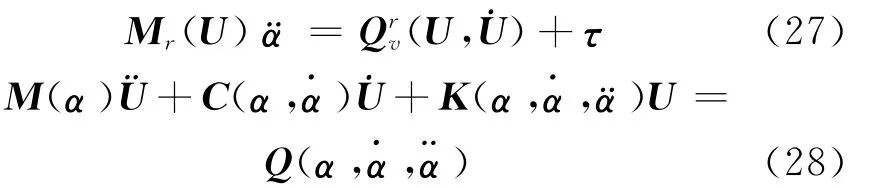
上两式中α＝［α1，α2，α3］T，U＝［U11，U12，…，U1n，…，U3n，ΔXP，ΔYP，Δε］T。

5 仿真计算

假设动平台的运动轨迹为

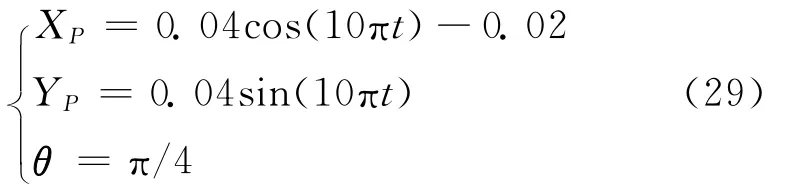
所有柔性杆件和动平台的材料都是硬铝合金，弹性模量为E＝0．7×105MPa，泊松比μ＝0．3，密度ρ＝2 712kg／m3，弹性杆件的横截面宽d＝0．04 m，高h＝0．01m，动平台厚c＝0．017 1m，L1＝AiBi＝0．245m，L2＝BiCi＝0．242m，L3＝CiP＝0．108m，L4＝AiP＝0．4m，i＝1，2，3，关节处的集中质量和集中转动惯量分别为0．15kg和0．000 5 kg·m2，假设系统的结构阻尼ζ＝0．003，每根柔性杆件被划分为3个梁单元，单元划分和节点坐标编号如图3所示。

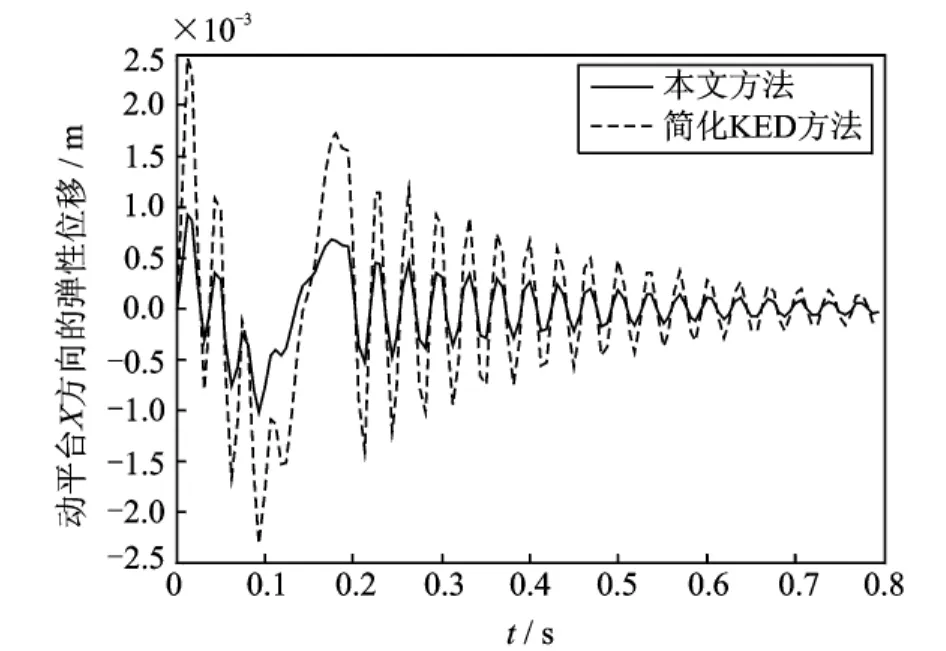
图4 动平台中心X方向弹性位移Fig．4 Xdirection elastic displacement of center of the moving platform

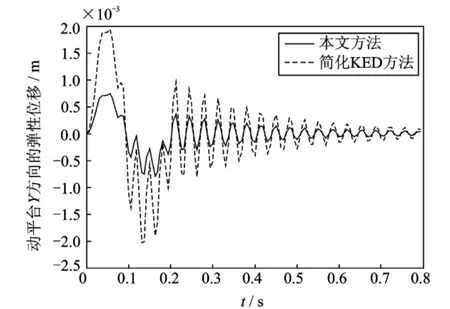
图5 动平台中心Y方向弹性位移Fig．5 Y direction elastic displacement of center of the moving platform

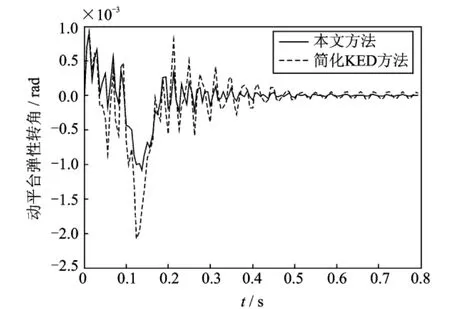
图6 动平台弹性转角Fig．6 Angle of deflection of the moving platform

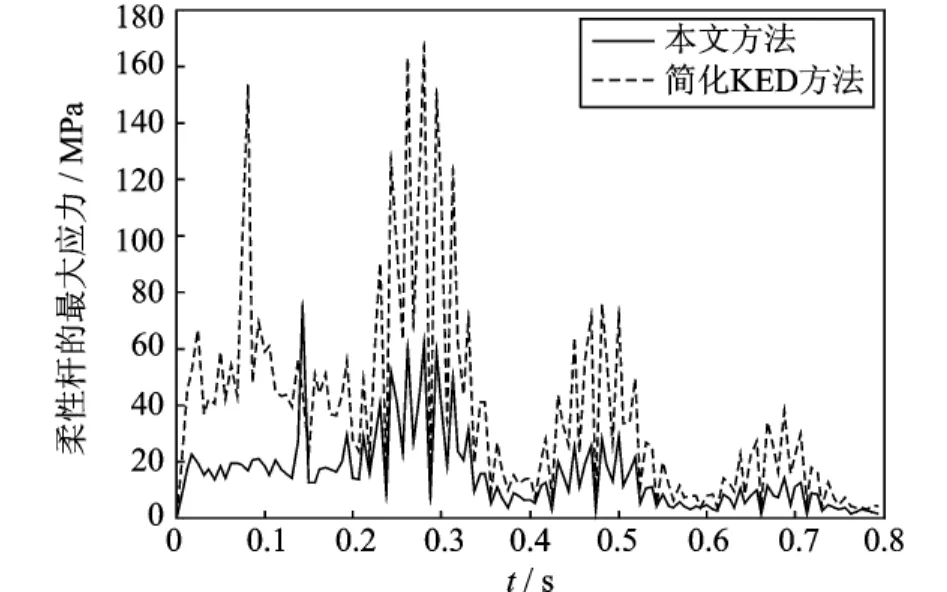
图7 弹性连杆的最大应力Fig．7 Maximal stress of the flexible links

采用KED假设，忽略机器人弹性变形运动对刚体运动的影响。用MATLAB软件进行仿真计算，并和简化KED方法的计算结果进行比较［4］。动平台按式（29）给定的圆轨迹运动一周后停止。仿真结果如图4～7所示，图中0～0．2s时间段的曲线分别表示系统运动时动平台中心沿X轴弹性振动位移、Y轴的弹性振动位移、动平台的弹性转角以及柔性连杆的最大应力变化，0．2～0．8s时间段的曲线是系统运行一周后动平台的残余振动情况和柔性连杆的最大残余应力变化情况。其中虚线表示简化KED方法的计算结果，实线表示本文方法的计算结果。从图4～7可知：采用本文的建模方法，在X方向，动平台中心的最大、最小弹性位移分别是0．916 4和－1．016mm；在Y方向，其最大、最小弹性位移分别是0．738 3和－0．797 8mm；动平台的最大、最小弹性转角分别是0．000 894 1和－0．001 087 rad；柔性连杆的最大应力为75．05MPa。而采用简化KED方法，在X方向，动平台中心的最大和最小弹性位移分别是2．464和－2．316mm；在Y方向，其最大、最小弹性位移分别是1．943和－2．027mm；动平台的最大、最小弹性转角分别是0．000 924 6和－0．002 071rad；柔性连杆的最大应力是167MPa。

分析图4～6，可知两种建模方法计算的弹性变形位移和柔性连杆的最大应力相差很大，主要原因是本文的建模方法考虑了科氏加速度和牵连加速度中的刚体运动对弹性运动的影响，同时由于坐标变换矩阵的时变性，从而引起系统的阻尼和刚度发生变化。同时还发现用本文的建模方法计算的弹性位移要小于简化KED方法计算得到的结果，那是因为本文建模方法考虑了变换矩阵的时变性以及计入了刚体运动的科式力和离心力，导致广义质量、阻尼、刚度以及广义外力矩阵发生变化，进而使得弹性位移减少。因此在建立平面3－RRR柔性并联机器人动力学模型时，不能过分地简化，科氏加速度等因素对系统弹性动力学特性的影响是至关重要的。比较发现，两曲线的变换趋势具有一致性，因此从定性分析层面讲，简化KED法具有一定的理论意义。

6 结束语

本文基于浮动坐标系法、有限元方法以及拉格朗日方程和虚功原理建立了平面3－RRR柔性并联机器人的弹性动力学模型，该模型考虑了刚体运动和弹性变形运动的耦合，详细考虑了刚体运动约束和弹性坐标约束关系，所建立的模型是二阶时变非线性耦合微分方程。结合具体实例，在给定动平台运动轨迹的情况下，运用Matlab软件求解了本文所建立的弹性动力学模型。在求解过程中，忽略了弹性变形运动对刚体运动的影响，计算了动平台的弹性位移和弹性转角和柔性连杆在不同位姿下的最大应力。通过比较本文的建模方法与简化KED方法，结果表明：刚体运动的科氏力和离心力以及坐标变换矩阵的时变性对系统动力学特性有至关重要的影响。实验平台正在搭建之中，今后将结合实验对平面3－RRR柔性并联机器人的弹性动力学建模作进一步地研究。对系统的耦合特性作更深入地分析。

［1］ Bruno Siciliano，Oussama Khatib．Springer Handbook of Robotics［M］．Berlin Heidelberg：Springer Press，2008．

［2］ Stewart D．A platform with 6degrees of freedom［J］．Proceedings of the Institution of Mechanical Engineers，1965，180（1）：371—386．

［3］ 胡俊峰，张宪民．两自由度高速并联机械手的弹性动力学分析［J］．华南理工大学学报（自然科学版），2009，37（11）：123—128．

Hu Junfeng，Zhang Xianmin．Elastodynamic analysis of a novel 2－DOF high－speed parallel manipulator［J］．Journal of South China University of Technology（Natural science），2009，37（11）：123—128．

［4］ 张策，黄永强，王子良，等．弹性连杆机构的分析与设计［M］．第2版．北京：机械工业出版社，1997．

Zhang Ce，Huang Yongqiang，Wang Ziliang，et al．A－nalysis and Design of the Flexible Linkage Mechanism［M］．2nd ed．Beijing：China Mechine Press，1997．

［5］ Zhang Xianmin，Liu Jike，Shen Yunwen．A high efficient frequency analysis method for closed flexible mechanism systems［J］．Mechanism and Machine Theory，1998，33（8）：1 117—1 125．

［6］ Zhang Xianmin，Liu Hongzhao，Shen Yunwen．Finite dynamic element analysis for high－speed flexible link－age mechanisms［J］．Computers ＆ Structures，1996，60（5）：787—796．

［7］ 杜兆才，余跃庆，张绪平．平面柔性并联机器人动力学建模［J］．机械工程学报，2007，43（9）：96—101．

Du zhaocai，Yu yueqing，Zhang xuping．Dynamic modeling of planar flexible manipulators［J］．Chinese Journal of Mechanical Engineering，2007，43（9）：96－101．

［8］ 刘善增．三自由度空间柔性并联机器人动力学研［D］．北京：北京工业大学，2009．

Liu Shangzeng．Dynamics of 3－DOF spatial flexible parallel robots［D］．Beijing：Beijing University of Technology，2009．

［9］ Piras G，Cleghorn W L，Mills Jeams K．Dynamic finite element analysis of a planar high－speed，high－precision parallel manipulator with flexible links［J］．Mechanism and Machine Theory，2005，40（7）：849—862．

［10］Wang Xiaoyun，Mills Jeams K．Dynamic modeling of a flexible－link planar parallel platform using a substructuring approach［J］．Mechanism and Machine Theory，2006，41（6）：671—687．

［11］Wang xiaoyun，Mills James K．A FEM model for active vibration control of flexible linkages［A］．Proceeding of IEEE International Conference on Robotics and Automation （vol．5）［C］．Piscataway，NJ，USA：IEEE，2004：4 308—4 313．

［12］Zhang xuping，Mills James K，Cleghorn W L．Study on the effect of elastic deformations on rigid body motions of a 3－PRR flexible parallel manipulator［A］．IEEE International Conference on Mechatronics and Automation［C］．Piscataway，NJ，USA：IEEE，2007：1 805—1 810．

［13］Shabana Ahmed A．Dynamics of Multibody Systems［M］．3rd ed．USA New York：Cambridge University Press，2005．