滚动轴承故障诊断的阶比多尺度形态学解调方法＊

徐亚军，于德介，孙云嵩，赵 丹

（湖南大学汽车车身先进设计制造国家重点实验室，湖南 长沙 410082）

引 言

滚动轴承是旋转机械中应用最为广泛的部件之一，各种旋转机械输出轴的支撑大多采用滚动轴承形式。滚动轴承的运行状态对整台机器的安全运行影响最大［1］，其运行状态的正常与否将直接影响到整个机组的性能，因此滚动轴承的状态监测和故障诊断技术研究具有重要的工程应用价值。

滚动轴承发生故障时，会产生周期性的脉冲冲击力，从而产生振动信号的调制现象，频谱图上表现为固有频率两侧出现间隔均匀的调制边频带［2］。传统的轴承故障诊断方法通过对轴承振动信号进行解调诊断故障。常用的软件解调方法有广义检波滤波解调、希尔伯特变换解调。在广义检波滤波解调分析中，由于取绝对值、检波过程或平方过程都会使载波频率有可能出现高次谐波而产生混频效应，因此需要选择合适的采样频率以避免这种混频效应［3］。Hilbert解调由于Hilbert算子的加窗效应，使得解调结果出现非瞬时响应特性，即在解调出的调制信号两端及有突变的中间部位产生调制，表现为幅值按指数衰减波动，从而使解调误差增大［4］。

数学形态分析是基于积分几何和随机集的非线性信号分析方法。该方法通过形态变换将一个复杂信号分解为具有物理意义的各个部分，使其与背景剥离，同时保留信号主要的形状特征［5］。数学形态学在考察信号时使用结构元素探针，通过结构元素探针在信号中不断移动来提取有用信息进行特征分析和描述［6，7］。多尺度形态学的结构元素由信号产生，具有一定的适应性，能更有效地提取信号的冲击特征［8～10］。对故障振动信号进行多尺度形态学操作，提取故障信号的冲击特征，然后进行频谱分析，能较好地达到解调的目的。与传统的解调分析比较，由于算法只涉及加减运算，不需要对信号进行绝对值、Hilbert算子等运算，一方面可以减少由于算子运算产生的混频效应、加窗效应等；另一方面降低了算法的复杂度。且不需要对运算结果进行低通滤波，无需预先选择截止频率，因此多尺度形态学解调是一种很好的解调分析方法。

根据轴承故障特征频率公式［11］，轴承故障特征频率与轴承的相关尺寸和转速相关。当转速变化时，轴承的故障特征频率会随转速一起变化，从而此时的故障特征频率不再是某一固定值，而是随时间变化的一条故障频率曲线。傅里叶变换以及其他的解调方法需要信号满足平稳化的要求，因此传统的轴承故障诊断方法不适用于转速变化情况下的轴承故障诊断。

Emmanuel J Candès等近年来提出的线调频小波路径追踪算法能有效提取信号的瞬时频率［12］。本文将线调频小波路径追踪算法与多尺度形态学解调方法相结合，提出了基于线调频小波路径追踪的阶比多尺度形态学解调方法，并用于转速大范围波动情况下的滚动轴承故障诊断。当滚动轴承发生故障时，其载波频率一般为外环的各阶固有频率，而调制频率为产生疲劳剥落元件（内环、外环或滚动体）的通过频率及其倍频［13］。本文方法先用线调频小波路径追踪算法估计转速波动滚动轴承的故障特征频率；再依据获得的通过频率对等时间间隔采样的滚动轴承振动信号进行插值和重采样，得到等角度采样的角域平稳信号；最后用信号局部峰值方法确定多尺度形态学分析的结构元素，根据各结构元素对重采样信号进行形态学操作，进而获得操作结果平均值的阶次谱以诊断滚动轴承故障。仿真信号和实验信号分析结果表明，基于线调频小波路径追踪的阶比多尺度形态学解调的方法可以有效地应用于滚动轴承的故障诊断。

1 线调频小波路径追踪算法

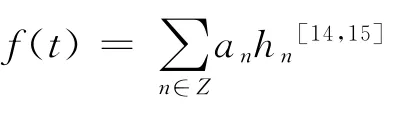
线调频小波路径追踪算法采用的多尺度线调频基元函数如下

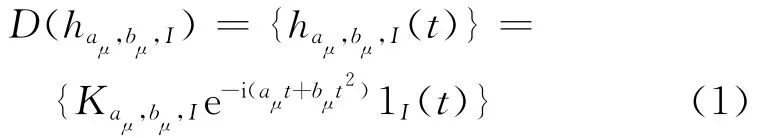
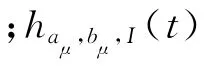
式（1）定义的多尺度线性调频基函数在动态分析时间段内的瞬时频率为aμ＋2bμt，在时频面的表示如图1所示。通过信号在多尺度线性调频基函数上的逐段投影分析，计算获得每个时间分析段I内的最大投影系数和对应的线调频基元函数，该基元函数即为在时间分析段I中与分析信号最为相似的频率成分，适合在小的动态分析时间段内逐段拟合频率呈曲线变化的频率成分。线调频基函数的多尺度特性使得它具有了动态匹配分析信号的特性，而基函数中包含的调频率信息则使得其适合分析频率呈曲线变化的非平稳信号。

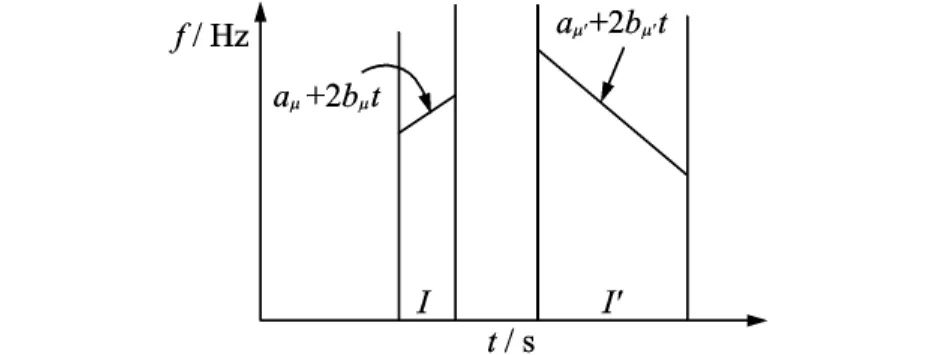
图1 基元函数的时频表示Fig．1 Time frequency representation of elementary function

当信号与多尺度线性调频基函数越相似时，其投影系数也越大，基元函数的能量也越大，因此要求找到一种动态分析时间段连接方法，在该连接方法下，使连接的所有基元函数信号在整个分析时间内的总能量最大，即

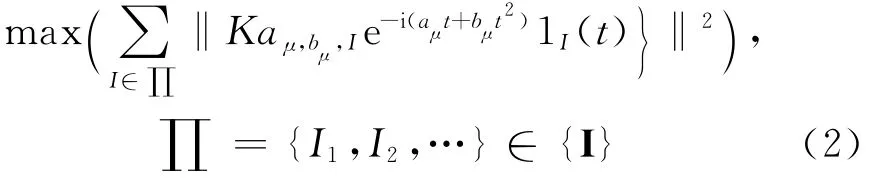
∏覆盖整个分析时间段，不能重叠，其对应的最大投影系数和基元函数分别为

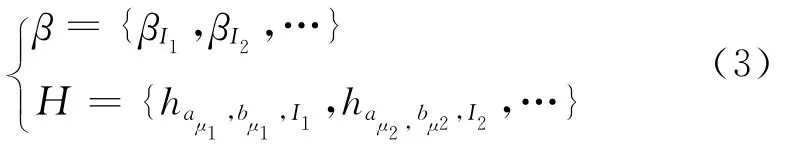
∏的连接方法应保证在投影中使连接的基函数在整个分析时间段内的总能量最大，线调频小波路径追踪算法提出的连接算法如下：

（1）初始化。以i为时间支持区序号，d（i）为第i个时间支持区之前分解信号的总能量，pre（i）为连接到第i个时间支持区的前置时间支持区序号，e（i）为第i个时间支持区最大投影系数对应的分解信号的能量，初始化时，置d（i），pre（i）＝0；

（2）对于动态分析时间段集合｛Ii，i∈Z｝中的每一个元素Ii，查找出与其相邻的所有下一个动态分析时间段集合｛Ij｝，即｛Ij｝中所有元素的起始时间与Ii相邻。如果

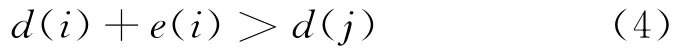
有

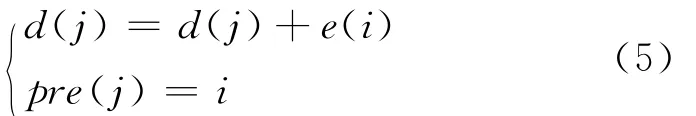
Π的连接方法可以保证在整个分析时间段内基元函数组合形成的信号与分析信号最为相似，而基元函数在动态分析时间支持区∏＝｛I1，I2，…｝内的瞬时频率为aμi＋2bμiti，ti∈Ii，对应的线性直线连接形成的频率曲线则是对分解信号的瞬时频率估计。

2 多尺度形态学及其计算

数学形态学有两种基本的形态函数：腐蚀和膨胀，若待处理信号x（n）是采样得到的一维多值信号，定义域为Df＝0，1，2，…，N－1，g（n）为一维结构元素序列，定义域为Dg＝0，1，2，…，M－1，其中N和M都是整数，且有N≥M。信号膨胀、腐蚀、开和闭运算分别定义为

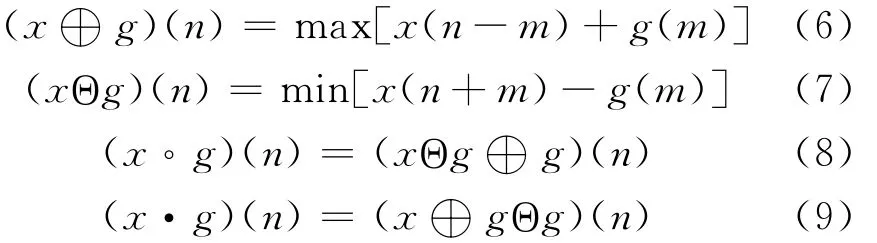
式中m∈0，1，2，…，M－1。

数学形态学的开运算可用于滤除信号上方的峰值噪声，去除信号边缘的毛刺；闭运算可用于平滑或抑制信号下方的波谷噪声，填补信号的漏洞和缝隙［16］。同时利用形态学开、闭运算可以构造AVG和DIF滤波器，构造方式分别为

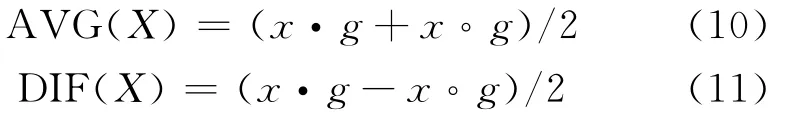
式中 AVG滤波器能用于信号正负冲击特征的平滑，相当于平滑滤波器，而DIF能用于提取信号的冲击特征［17］。

令x和B分别代表一维信号和形态学的结构元素，若给定了一个二值形态学变换T，则基于T的多尺度形态学运算可定义为一族形态学变换｛Tλ｜λ＞0，λ∈N｝，其中Tλ（x）＝λT（x／λ），相似地，多尺度形态学膨胀、腐蚀操作定义为

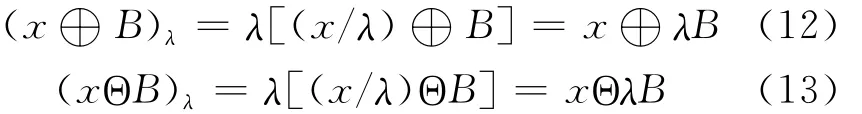
式中λB＝B⊕B⊕…⊕B（λ－1次），参照传统的多尺度形态学在图像处理中的应用，定义长度尺度λl和高度尺度λh，即λ＝（λl，λh）。对长度尺度λl和高度尺度λh的搜索，本文采用局部极值自适应搜索方法，得到长度尺度λl的最大值和最小值分别为

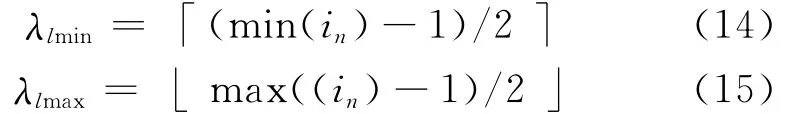
因此长度尺度λl＝｛λlmin，λlmin＋1，…，λlmax｝，其中in为极值间隔，高度尺度λh定义为

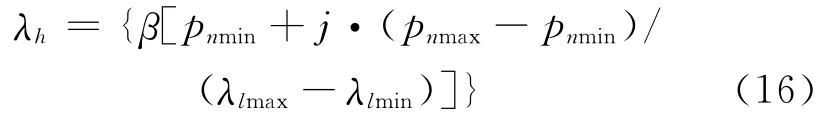
式中j＝0，1，2，…，λlmax－λlmin，其中pnmin，pnmax分别为信号的最大和最小值。β为尺度的幅值系数，（0＜β＜1），本文取β＝1／3。利用λl和λh构建多尺度形态学的每一个尺度的结构元素λB为

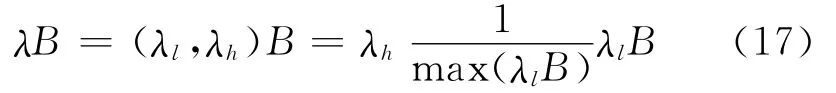
式中λlB是将B进行λl－1次膨胀运算。

本文选取的形态学算子为差值算子DIF，结构元素B为三角型结构元素，B＝［0，1，0］。则

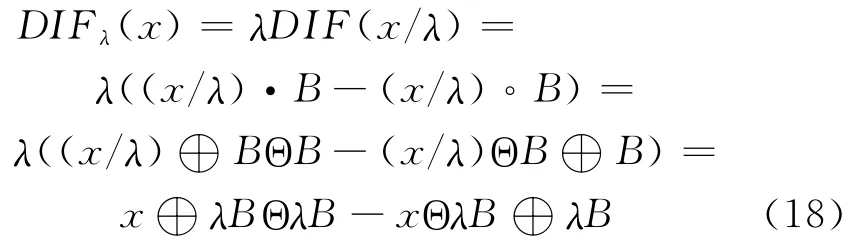
3 基于线调频小波路径追踪的阶比多尺度形态学解调

多尺度形态学DIFλ操作能有效地提取信号的冲击特征，若对滚动轴承故障信号进行多尺度形态学操作，提取故障信号的冲击特征，然后进行频谱分析，则能较好地达到解调的目的。但是频谱分析是以分析稳态信号为前提的，而变转速工况下拾取的轴承振动信号为非平稳信号。因此本文结合线调频小波路径追踪方法和多尺度形态学分析，提出基于线调频小波路径追踪的多尺度形态学解调方法。

信号等角度重采样的具体步骤为：

（1）采用线调频小波路径追踪方法分析滚动轴承振动信号，获得变转速滚动轴承振动信号的故障特征频率曲线；

（2）用三阶多项式对特征频率曲线进行拟合，则有

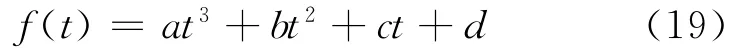
（3）确定阶次跟踪的最大分析阶Dmax；

（4）计算等角度重采样的角度间隔Δθ，根据采样定理，采样率应不小于最大分析阶次的两倍，所以

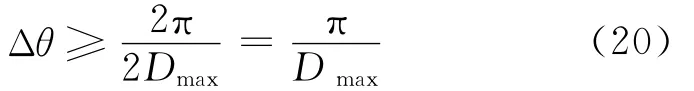
（5）计算重采样后数据的长度N

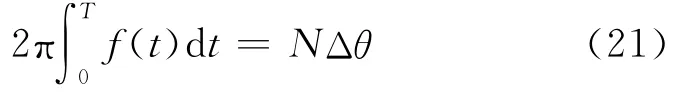
式中T为时域采样的总时间，f（t）为频率拟合函数；

（6）计算等角度重采样的键相时标Tn

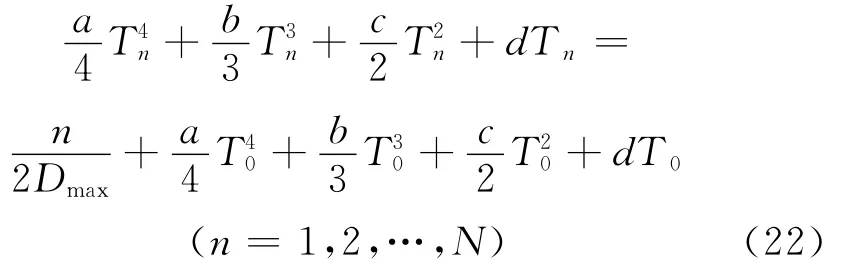
式中T0为时域采样开始时间；

（7）等角度重采样，根据所求出的键相时标Tn，利用Lagrange线性插值公式对振动信号进行插值，求出振动信号在角域里对应于键相时标Tn的幅值。对于给定的插值节点Tn及对应的幅值x（Tn），则Lagrange线性插值公式为

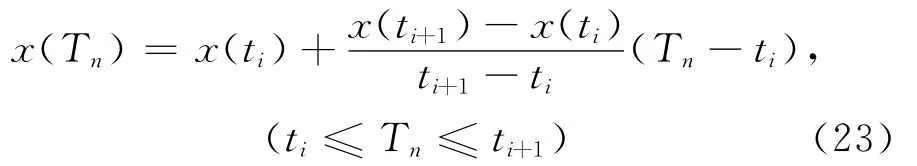
经以上步骤得到重采样信号x（Tn）后，用信号局部极值自适应搜索方法得到重采样信号x（Tn）的长度尺度和高度尺度，再利用式（17）即可构建多尺度形态学DIFλ操作的每一个尺度的结构元素λB。

根据式（18）分别计算出分析信号x（Tn）的各个尺度形态学分析结果，其反映了分析信号中含有的特定尺度的冲击成分，在每一尺度的分析结果中也会含有随机噪声。对于特定的信号x（Tn），其冲击成分应该出现在多个尺度中，因此将各个尺度的形态学分析得到的信号取平均值作为最终的多尺度形态学操作结果，这样既突出信号中的冲击成分，又有效地抑制了噪声。最后对平均后的多尺度形态学操作结果做频谱分析，便完成了对滚动轴承故障信号的阶比多尺度形态学解调。

基于线调频小波路径追踪的阶比多尺度形态学解调过程可用图2所示的原理框图表示。

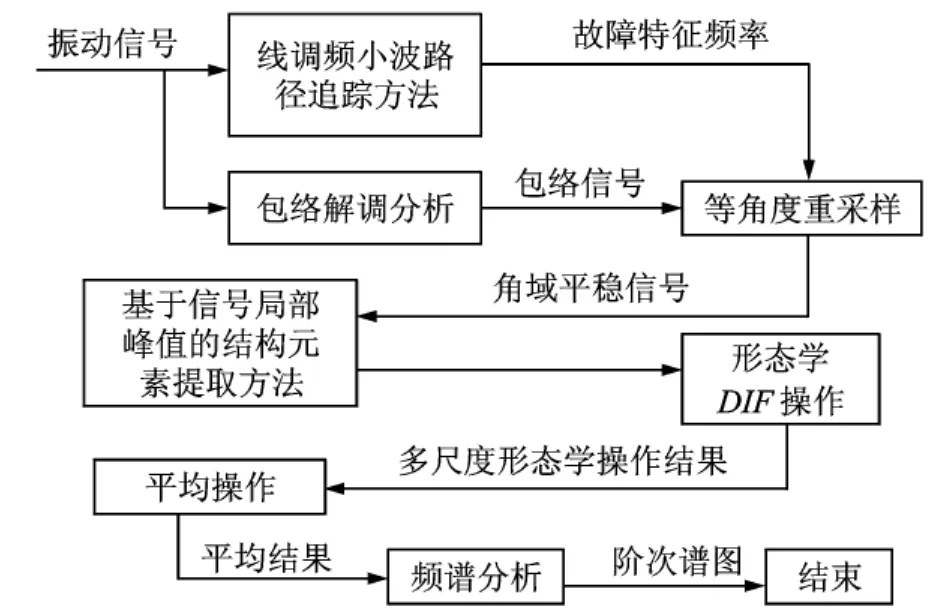
图2 基于线调频小波路径追踪的阶比多尺度形态学解调原理框图Fig．2 The schematic diagram of the order multi－scale morphology demodulation based on chirplet path pursuit algorithm

4 仿真信号分析

为验证本文方法的有效性，对一轴承故障仿真信号进行分析。当轴承出现故障时，振动信号中会出现以轴承元件固有频率为载波频率的多频率调制信号，通常表现为不断重复的脉冲衰减信号，当轴承转速变化时，脉冲出现的间隔即调制频率会随转速变化。

取脉冲信号为

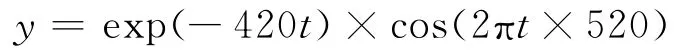
信号载波频率为1 020Hz，衰减系数为－420。为模拟轴承振动信号被调制信号调制的现象，假定载波信号幅值被频率f1调制，取调制频率f1为

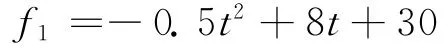
图3为单个脉冲信号时域波形图，通过构建repeat函数来实现每隔周期1／f1出现单个脉冲，即可组成周期脉冲信号。图4为加噪仿真信号时域波形示意图，信号采样频率为8 192Hz，采样时长4s，信噪比10dB。对加噪仿真信号进行希尔伯特变换，得到包络信号，因脉冲调制频率最大为54Hz，所以将包络信号采样频率由原来的8 192降为1 024Hz，对于脉冲调制频率的提取仍能满足采样定理。图5为用FFT变换得到的降采样包络信号频谱图，由于脉冲调制频率随时间变化，从该图很难直接对调制频率进行识别。图6为仿真信号的调制频率和拟合频率时频图，图中实线是仿真信号的调制频率曲线，虚线为对包络信号用线调频小波路径追踪方法提取的调制频率拟合曲线。从图中不难看出拟合频率曲线很好地匹配了信号的调制频率曲线。将信号以线调频小波路径追踪方法提取的调制频率进行等角度重采样，对重采样信号进行多尺度形态学解调，再对解调信号做阶次谱就得到图7所示的仿真信号的多尺度形态学解调阶次谱。图中阶次1，2，3，4恰好对应着模拟故障特征频率及其倍频，从而很好地验证了本文方法的有效性。

图3 脉冲信号时域波形图Fig．3 The time domain waveform diagram of pulse signal

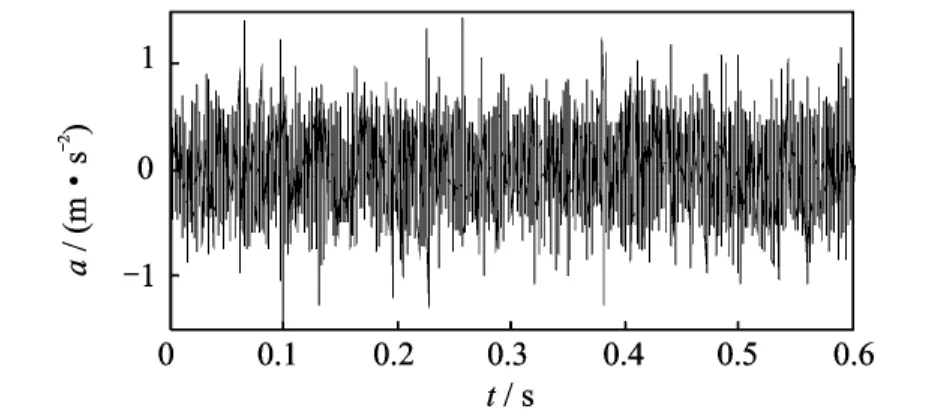
图4 仿真信号时域波形图Fig．4 The waveform of simulated signal

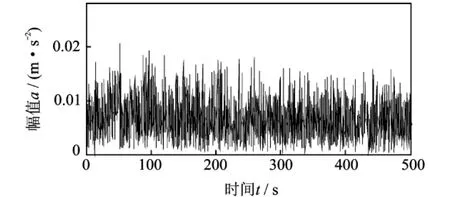
图5 包络信号频谱图Fig．5 Spectrogram of the envelope signal

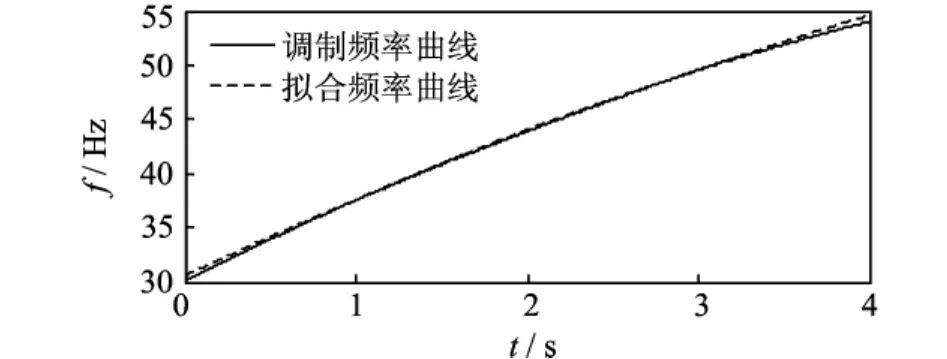
图6 仿真信号的调制频率和拟合频率时频图Fig．6 The time－frequency diagram of the simulation signal’s modulation frequency and fitting frequency

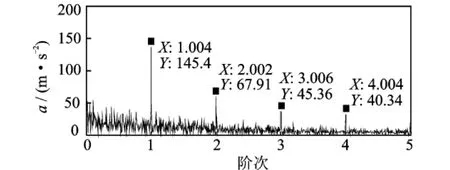
图7 仿真信号的多尺度形态学解调阶次谱Fig．7 The order spectrum of the simulation signal obtained by multi－scale morphology demodulation

图8中实线是仿真信号的调制频率曲线，虚线为仿真信号基于Wigner－Ville峰值跟踪算法得到的拟合频率曲线，与基于线调频小波路径追踪方法得到的调制频率曲线（图6）相比，其精度明显要低。

图9为仿真信号基于Wigner－Ville的包络阶次谱，图中出现了（2．705，77．08），（3．599，62．39）的干扰阶次。可见在信噪比较低的情况下，基于线调频小波路径追踪的阶比多尺度形态学解调方法能得到更准确的阶次谱。

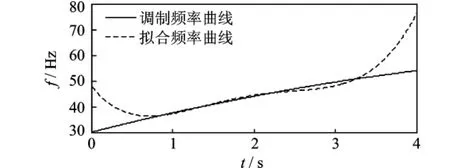
图8 仿真信号的调制频率与 Wigner－Ville峰值跟踪算法的拟合频率Fig．8 The modulation frequency and the fitting frequency obtained by Wigner－Ville peak tracking algorithm of the simulation signal

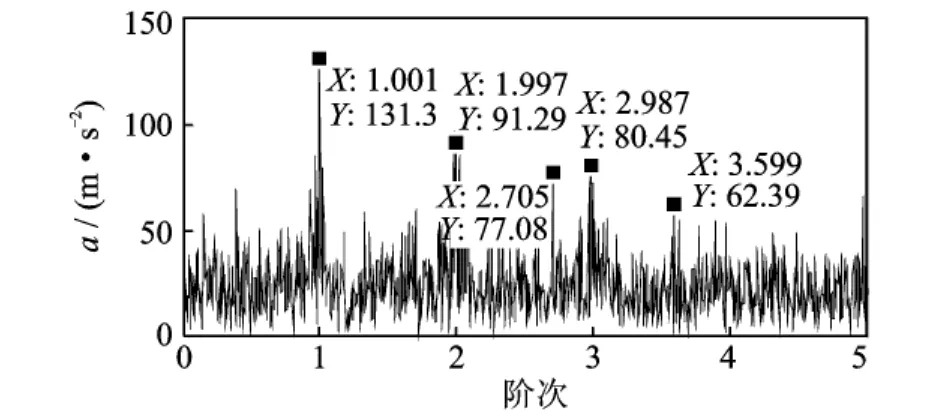
图9 基于Wigner－Ville峰值跟踪的包络阶次谱Fig．9 The envelope order spectrum based on Wigner－Ville peak tracking algorithm

5 实测滚动轴承故障振动信号分析

试验轴承为6307E型滚动轴承，利用激光分别在外圈和内圈上切割宽0．15mm，深0．13mm的槽，模拟外圈和内圈故障，由于试验条件的限制，未能在滚动体上设置故障。振动加速度传感器固定在轴承座正上方，拾取轴承外圈和内圈故障振动信号时，转速分别在809．09～1 280．60r／min之间和340．72～714．91r／min之间变化，采样频率8 192 Hz，采样时长为4s。滚动轴承试验台如图10所示。

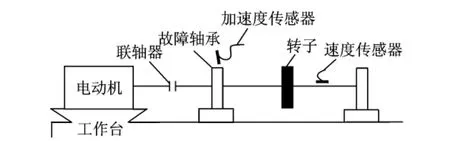
图10 滚动轴承试验装置Fig．10 The experiment device of rolling bearing

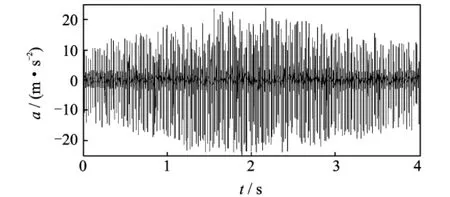
图11 轴承外圈故障振动信号时域波形图Fig．11 The time domain vibration signal of bearing outer race fault

图11为轴承外圈故障振动信号的时域波形图，从图中可以看出存在明显的冲击脉冲，且脉冲间隔随转速变化。图12中曲线分别为用转速计实测的故障轴承所在轴转频曲线（曲线1）和根据轴承故障特征频率计算公式计算获得的轴承外圈故障特征频率曲线（曲线2）［11］，可以看出转频在13．48～21．34 Hz间变化，故障特征频率随转速波动在41．26～65．31Hz之间变化。图13为传统的包络信号频谱图，由于故障特征频率随转速变化，无法准确判断其峰值点属于转频及其倍频还是故障特征频率及其倍频。将包络信号的采样频率由8 192Hz降为1 024 Hz，对于10倍故障特征频率的提取仍能满足采样定理。当滚动轴承外圈发生故障时，其载波频率一般为外环的各阶固有频率，而调制频率为外环的通过频率及其倍频［13］。图14中实线为图12中计算得到的故障特征频率曲线，虚线是降采样的包络信号经过线调频小波路径追踪方法分解得到的拟合频率曲线。从图中可以看出其能很好地匹配根据转频计算得到的故障特征频率曲线。以图14中虚线所示频率曲线对外圈故障信号进行等角度重采样，对重采样信号进行多尺度形态学解调，再对解调信号进行阶次谱分析，得到外圈故障信号的阶比多尺度形态学解调阶次谱如图15所示，图中的峰值谱线对应外圈故障特征频率及其倍频的阶次，从图中能很清晰地辨别出故障特征频率及其倍频，表明轴承信号被外圈故障特征频率及其倍频成分调制了，这正是一般滚动轴承出现外圈故障时的振动信号特征，与实际情况相符。

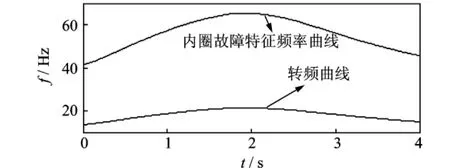
图12 轴转动频率与轴承外圈故障特征频率曲线图Fig．12 The Shaft rotation frequency and bearing outer race fault characteristic frequency

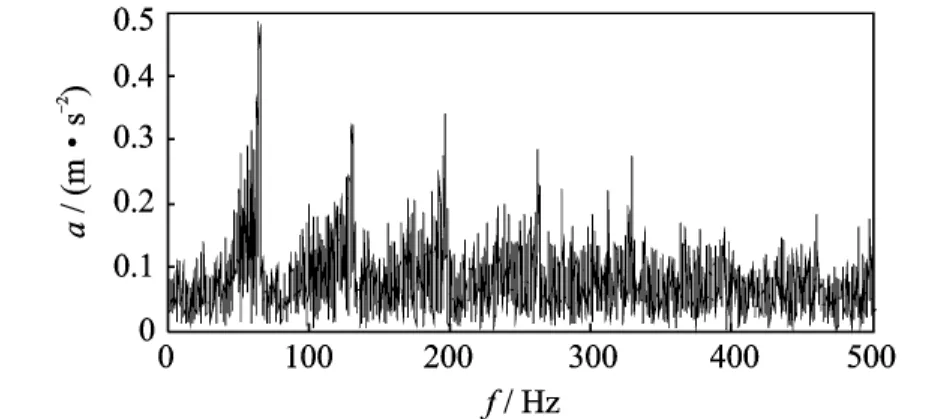
图13 外圈故障包络信号频谱图Fig．13 The envelope spectrum of bearing outer race fault’s vibration signal

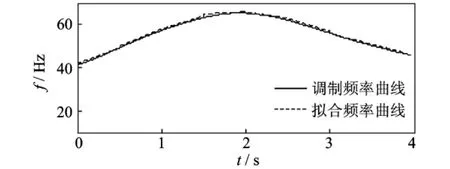
图14 外圈故障特征频率曲线Fig．14 The characteristic frequency of the bearing outer race fault

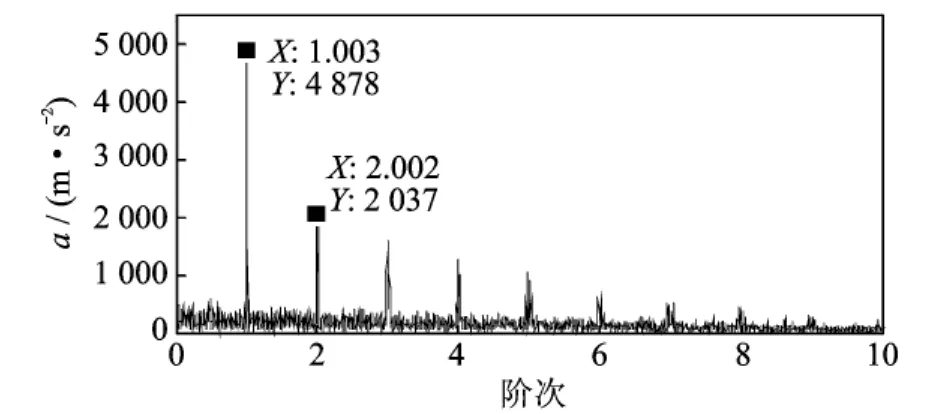
图15 外圈故障信号多尺度形态学解调阶次谱Fig．15 The order spectrum of the bearing outer race fault signal obtained by multi－scale morphology demodulation

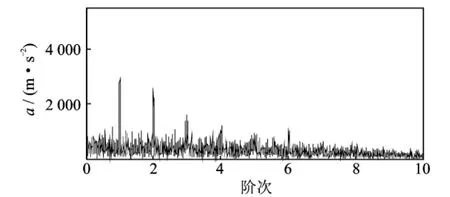
图16 外圈故障信号的包络阶次谱Fig．16 The envelope order spectrum of the bearing outer race fault signal

同样以图14中虚线所示频率曲线对外圈故障信号进行等角度重采样，再对解调信号进行阶次谱分析得到图16所示的外圈故障信号的包络阶次谱。比较图15与16，可以看出图15中的阶次更加清晰、明显，既突出了冲击成分，又有效地抑制了噪声。从而可以验证阶比多尺度形态学对于轴承故障诊断的优越性与有效性。

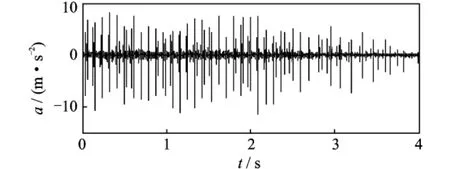
图17 轴承内圈故障振动信号时域波形图Fig．17 The time domain vibration signal of bearing inner race fault

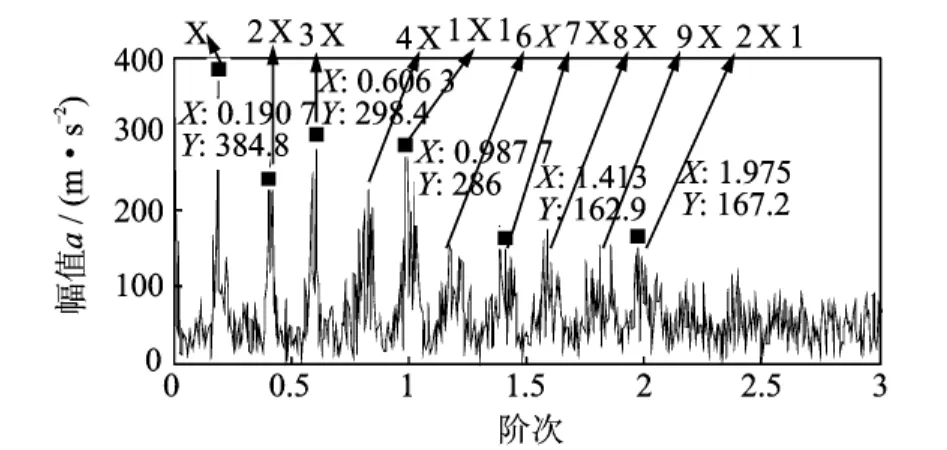
图18 内圈故障信号多尺度形态学解调阶次谱Fig．18 The order spectrum of the bearing inner race fault signal obtained by multi－scale morphology demodulation

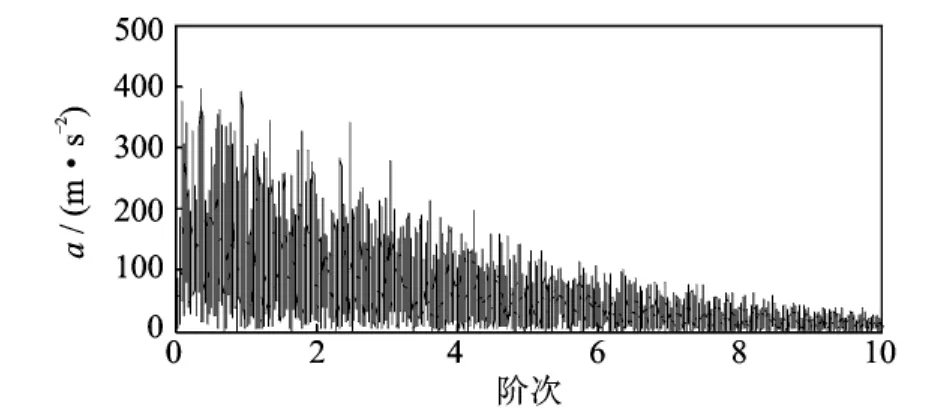
图19 内圈故障信号基于Wigner－Ville的包络阶次谱Fig．19 The envelope order spectrum of the bearing inner race fault signal based on Wigner－Ville

图17是含有内圈故障的滚动轴承振动加速度信号。当滚动轴承内圈出现故障时，其载波频率一般为外环的各阶固有频率，调制频率为内环的通过频率及其倍频以及转频及其倍频［13］。图18为内圈故障振动信号基于线调频小波路径追踪的多尺度形态学解调阶次谱。阶次谱中出现了1X1（0．992 5），2X1（1．975）的阶次，这与故障特征频率的1，2倍频极为吻合。同时也出现了0．190 7，0．410 7等阶次，这是振动信号被转频及其倍频调制的结果。实际上，根据轴承故障特征频率公式和轴承型号（6307E）［11］，计算得到内圈的故障特征频率是转频的4．937倍（则转频为故障特征频率的1／4．937≈0．202），阶次谱中出现的 X（0．190 7），2X（0．410 7），3X（0．603 3），4X（0．810 6），6X（1．210 8），7X（1．414 3），8X（1．602 1），9X（1．821 4）的阶次为转频及其倍频。

用基于Wigner－Ville峰值的阶比跟踪方法对内圈故障信号进行包络阶次谱分析，结果如图19所示，其阶次基本上不能区分出来，已淹没在噪声中。可见在内圈故障振动信号信噪比较低的情况下，基于线调频小波路径追踪的阶比多尺度形态学解调效果要明显优于基于Wigner－Ville的阶比跟踪效果。

6 结 论

（1）线调频小波路径追踪算法能在不额外安装硬件的情况下得到轴承的故障特征频率曲线，从而能将转速波动的非平稳振动信号转化为角域的平稳信号，降低了滚动轴承故障诊断的复杂度，节约了成本。用线调频小波路径追踪算法获得轴承故障特征频率曲线的过程不会受到二次时频交叉干扰项的影响，不需要通过带通滤波器对其他频率分量进行“掩盖”，使得其估计精度高于峰值跟踪法。

（2）多尺度形态学的尺度系数由信号产生，具有一定的自适应性，能够提取振动信号中含有的特定尺度的冲击成分，对各尺度形态学分析结果取平均能有效抑制噪声，因此多尺度形态学阶次分析比包络阶次分析更能有效地突出冲击成分，抑制噪声。

（3）仿真与应用实例表明，将线调频小波路径追踪算法和多尺度形态学解调方法相结合，能很好对变转速下的滚动轴承外圈与内圈故障进行识别。

［1］ 钟秉林，黄仁．机械故障诊断学［M］．北京：机械工业出版社，2007．

Zhong Bing－lin，Huang Ren．Mechanical Fault Diagnosis［M］．Beijing：China Machine Press，2007．

［2］ 丁康，孔正国．振动调幅调频信号的调制边频带分析及其解调方法［J］．振动与冲击，2005，24（6）：9—12．

Ding Kang，Kong Zheng－guo．Modulation principle of amplitude and frequency modulated signal and its demodulation procedure［J］．Journal of Vibration and Shock，2005，24（6）：9—12．

［3］ 张帆，丁康．广义检波解调分析的三种方法及其局限性研究［J］．振动工程学报，2002，15（2）：243—248．

Zhang Fan，Ding Kang．Research on the three algorithms and limitations of generalized detection－filtering demodulation analysis［J］．Journal of Vibration Engineering，2002，15（2）：243—248．

［4］ 刘红星，陈涛，屈梁生，等．能量算子解调方法及其在机械信号解调中的应用［J］．机械工程学报，1998，34（5）：85—90．

Liu Hong－xing，Chen Tao，Qu Liang－sheng，et al．Energy operator demodulation method and its application in mechanical signal demodulation［J］．Chinese Journal of Mechanical Engineering，1998，34（5）：85—90．

［5］ 龚炜，石青云，程民德．数字空间中的数学形态学——理论及应用［M］．北京：科学出版社，1997．Gong Wei，Shi Qing－yun，Chen Min－de，Theory of Mathematical Morphology in Digital Space and Its Application［M］．Beijing：Science Press，1997．

［6］ NIKOLAOU N G，ANTONIADIS I A．Application of morphological operators as envelope extractors for impulsive－type periodic signals［J］．Mechanical Systems and Signal Processing，2003，17（6）：1 147—1 162．

［7］ SUSANTA M，BHABATOSH C．A multiscale morphological approach to local contrast enhancement［J］．Signal Processing，2000，80：685—696．

［8］ Mukhopadhyay S，Chanda B．An edge preserving noise smoothing technique using multiscale morphology［J］．Signal Processing，2002，82（4）：527—544．

［9］ Zhang Lijun，Xu Jinwu，Yang Jianhong，et a1．Multiscale morphology analysis and its application to fault diagnosis［J］．Mechanical Systems and Signal Processing，2008，22：597—610．

［10］林京，屈梁生．基于连续小波变换的信号检测技术与故障诊断［J］．机械工程学报，2000，36（12）：95—100．

Lin Jing，Qu Liang－sheng．Feature detection and fault diagnosis based on continous wavelet transform［J］．Chinese Journal of Mechanical Engineering，2000，36（12）：95—100．

［11］MALLAT S，ZHANG Z．Matching pursuit with timefrequency dictionaries［J］．Signal Processing，1993，41（12）：3 397—3 415．

［12］Candès E J，Charlton P R，Helgason H．Detecting highly oscillatory signals by chirplet path pursuit［J］．Applied and Computational Harmonic Analysis，2008，24（1）：14—40．

［13］PAN Minchun，CHIU Chunching．Investigation on improved Gabor order tracking technique and its applications［J］．Journal of Sound and Vibration，2006，295（3－5）：810—826．

［14］Candes E J，Charltion P R，Helgason Hannes．Detecting highly oscillatory signals by chirplet path pursuit［J］．Applied and Computational Harmonic Analysis，2008，24（1）：14—40．

［15］Qian S，Chen D．Joint Time－Frequency Analysis［M］．Englewood Cliffs，Prentice Hall，1996．

［16］章立军，徐金梧，阳建宏．自适应多尺度形态学分析及其在滚动轴承故障诊断中的应用［J］．北京科技大学学报，2008，30（4）：441—445．

Zhang Li－jun，Xu Jin－wu，Yang Jian－hong．Adaptive multiscale morphology analysis and its application in fault diagnosis of bearing［J］．Journal of Beijing University of Science and Technology，2008，30（4）：441—445．

［17］郝如江，卢文秀，褚福磊．滚动轴承故障信号的数学形态学提取方法［J］．中国电机工程学报，2008，28（6）：65—70．

Hao Ru－Jiang，Lu Wen－xiu，Chu Fu－lei．Mathematical morphology extracting method on roller bearing fault signals［J］．Proceedings of the CSEE，2008，28（6）：65—70．