针对脑部电阻抗成像的四种正则参数选取方法的比较研究*
2013-09-12李彦东徐灿华董秀珍
李彦东 杨 滨 徐灿华 代 萌 付 峰 董秀珍
电阻抗成像(electrical impedance tomography,EIT)是一种无创的医学成像技术,其基本原理是根据人体内不同组织在不同的生理、病理状态下具有不同的电阻(导)率,通过各种方法给人体施加小的安全驱动电流(电压),在体外测量响应电压(电流)信号以重建人体内部的电阻率分布或其变化的图像[1]。与传统医学成像技术CT、MRI等相比,EIT具有成本低、无创无损伤以及能够对患者进行长时间实时监护等优点。因此,EIT在脑部持续性、迟发性出血类疾病中可展现出良好的临床应用前景[2-6]。
由于EIT的逆问题具有严重的不适定性,图像重构矩阵具有很大的条件数,同时由于系统噪声和建模误差的存在,测量边界电压信号的微小变化也会造成重构阻抗分布的剧烈变化。高阻抗颅骨对激励电流的阻挡作用加大了逆问题的不适定性,使得内部的电阻抗变化更难体现在边界电压的变化上[7-9]。目前,广泛使用的方法是通过各种正则化方法(如先验正则化方法、图像平滑等)降低重构矩阵的条件数,尽可能求取接近精确解的近似解,从而得到稳定而精确的图像[10]。该类方法重建图像的稳定程度和精确程度依赖于正则化参数,因此选取适当的正则化参数则成为获取最优近似解的重要途径。
在EIT领域正则化参数选取方法研究上,Graham等[11]用仿真的方法,在二维圆域且内部阻抗呈均匀分布的情况下仿真比较了L型曲线法(L-curve)、广义交叉校验法(generalized cross-validation,GCV)、固定噪声系数法和偏差原理法等4种方法,得出固定噪声系数法(fixed noise figure,FNF)是较好的正则化参数选取方法;Abascal等[12]对真实边界的三维模型进行了剖分和仿真,比较了L型曲线法等4种方法,得出L型曲线法和广义交叉校验法效果好,并将其运用到婴儿脑部电阻抗成像中,得到了较好的成像结果。研究显示,Graham等[11]的研究是针对圆域均匀模型,Abascal等[12]的研究是针对三维真实边界阻抗均匀分布的模型,二者均未考虑高阻抗颅骨对正则化参数选取方法的影响,且得到的结论并不相同。因此,本研究拟通过含高阻抗颅骨的真实颅脑模型,比较L型曲线法、广义交叉校验法、固定噪声系数法、偏差原理(discrepancy principle,DP)4种方法的效果,希望得出一种适用于脑部EIT的正则参数选取方法。
1 EIT图像重建
EIT图像重建是通过边界电压求解内部阻抗分布或阻抗变化,即通过方程Ax=y求取其中的x。由于逆问题的不适定性,通常采用正则化技术求解。目前,广泛采用的L2正则化技术,是通过最小化泛函(公式1):
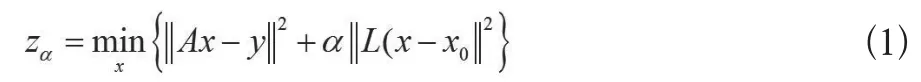
来求解反问题。式中,L为特定连续二乘函数形成的正则化矩阵,x0表示模型参数x的初值,α为正则化参数。其相应的正则化解为(公式2):
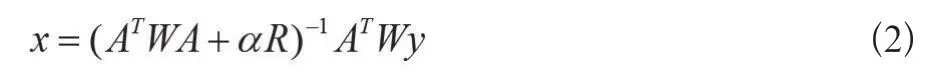
式中W为加权矩阵,R为正则化矩阵,该矩阵与相应的先验信息有关,一般可取单位对角矩阵、高通高斯滤波矩阵、拉普拉斯滤波矩阵、对角矩阵[R]对角矩阵等[13]。
2 正则参数对图像重建的影响
区域内重构阻抗大于半高宽的单元可以量化反映重构图像的效果,因此,仅将重构值大于半高宽的单元显示出来(黑色),当正则参数过小时,大于半高宽的单元分布比较分散;随着正则参数的增大,大于半高宽的单元逐渐聚拢,当正则参数取得合适的值时,大于半高宽的单元面积取得最小;而当正则参数继续增大,大于半高宽的单元不再聚拢而是扩散。因此,选取合适的正则参数才能重建出理想的图像(如图1所示)。
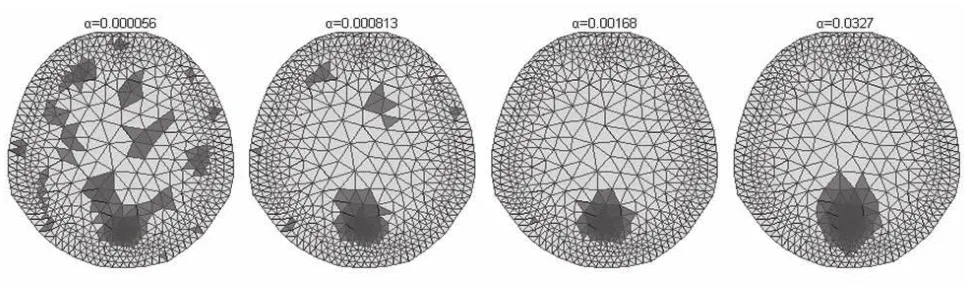
图1 不同正则参数下的重构图像
3 四种正则化参数选取方法
3.1 L型曲线法
该方法是最为广知的选取正则参数的方法,其以解范数的对数lg‖xα‖和残余范数的对数lg‖Axα-y‖的关系曲线对比来确定正则参数。该曲线往往呈一个明显的L型,故名L型曲线法。运用L型曲线准则的关键是求取曲线的隅角,该隅角反映了极小化残差‖Axα-y‖与极小化解模‖xα‖之间的平衡。令ρ=lg‖Axα-y‖,θ=lg‖xα‖,则曲率关于正则参数α函数可定义为(公式3):

其中“'”表示关于α的微分。曲率等于最大值对应的α即为最优正则化参数。
3.2 广义交叉校验法
广义交叉验证法的基本思想是,如果将任意一个观测值Li从观测序列L中删除,则此时由剩余观测值求得的正则化解应能够较好地预测L中被去掉的这一观测值Li。广义交叉验证可以等效为求解最小GCV问题(公式4):

式中,“Tr(·)”表示求矩阵的迹,B使得xα=By得到满足。当GCV函数达到极小值时,对应的α即为最优正则化参数。
3.3 固定噪声系数法
固定噪声系数法是基于1996年Adler和Guardo提出的噪声系数(Noise Figure,NF)[14],该参数被定义为测量信噪比和图像信噪比的比值(公式5):
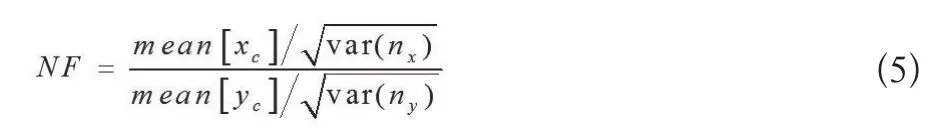
上式中信号定义为yc=Axc,xc为一个小的在区域中心的阻抗变化。一般情况下,取NF=0.5~2所对应的正则化参数。
3.4 偏差原理
很多情况下,原始资料y中的误差水平的参数δ往往是可以获取或近似获取的,在这种情况下,我们可以通过偏差方程(公式6):

记p(α)=‖Axα-y‖2-δ2,对p(α)在α=αn作泰勒展开并在三阶处截断,则有(公式7):
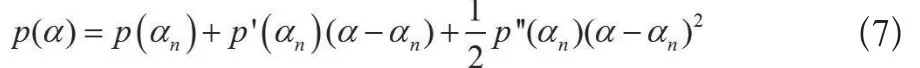
结合式(6)、(7)得出偏差原理的迭代公式,且该式是三阶收敛的[15](公式8):
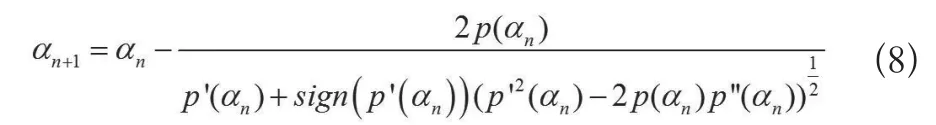
设置合适的初始正则参数,运用(8)式迭代数次即得最优化正则参数。
4 不同算法的量化比较
不同的方法是通过模糊半径和重建位置误差来进行比较的(公式9):
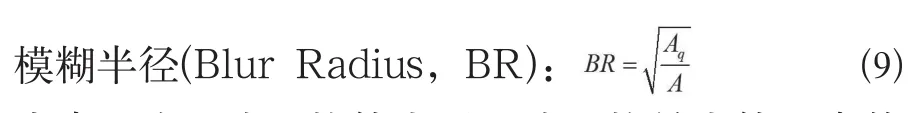
式中Aq为重建阻抗值大于重建阻抗最大值一半的面积,A为整个脑部的面积,分辨率反映了图像重建的精度。
位置误差(position error,PE)反映了重构目标与真实目标的位置偏移程度。
为使结果有统计学意义,对边界电压施加50次不同的0.1%的高斯白噪声,对L型曲线法、GCV、NF法和偏差原理法4种方法进行比较,结果以(均值±均方差)的形式给出。
5 结果
5.1 数据来源
研究所采用的仿真模型是用有限元方法生成的,模型如图2(a)所示。为了模拟高阻抗颅骨的真实颅脑模型,模型中的阻抗分布是非均匀的,电阻率值设置为∶皮肤∶颅骨∶脑实质=2.27 Ωm∶25.64 Ωm∶3.33 Ωm[4],在颅脑的边界等间距均匀设置16个电极,采用对向驱动模式,激励电流为1mA。根据重建需要,在真实颅脑模型中2/3半径处设置了低于脑实质阻抗的电阻抗变化,电阻率大小设置为1.48 Ωm(模拟颅内出血)[4],如图2(b)所示。由于正逆问题采用同样的模型会产生逆问题补偿,因此本研究采用图2(c)中的逆问题模型重建图像。

图2 全脑剖分模型
5.2 一例重建结果
为进一步阐述不同方法的结果,取出一例重建结果进行展示。如图3所示,展示了正则参数连续变化的影响。对于小的α,残差‖Axα-y‖较小(图3a)但是解模‖xα‖较大(图3b);与之相应,对于大的α,残差‖Axα-y‖较大(图3-a)但是解模‖xα‖较小(图3-b);图3-c为L型曲线的曲率与正则参数的关系,图中曲率最大值对应的正则参数即为最优正则参数;图3-d为GCV函数与正则参数的关系,图中函数极小值对应的正则参数为最优正则参数。
4种方法求得的最优正则参数在L型曲线上的位置如图4所示。
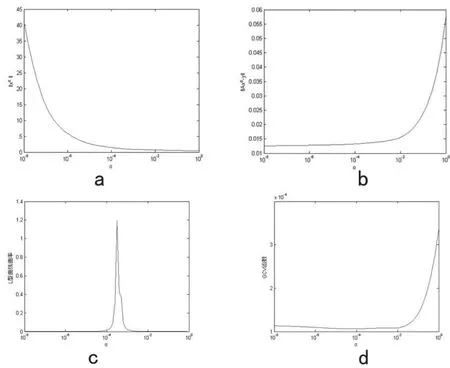
图3 向边界电压添加0.1%高斯白噪声的一例重建结果
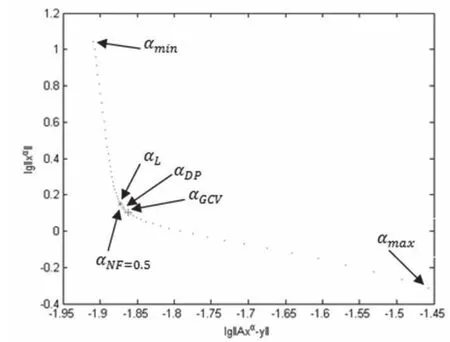
图4 4种方法选取的正则参数在L型曲线上的位置
4种方法选取的正则参数下重建得到的图像如图5所示。
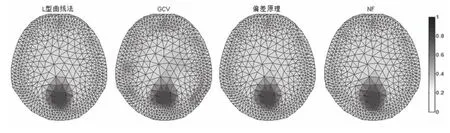
图5 4种方法重构内部阻抗的归一化显示
5.3 不同方法的统计结果
本研究添加50次不同的0.1%高斯白噪声的不同方法的统计结果见表1。
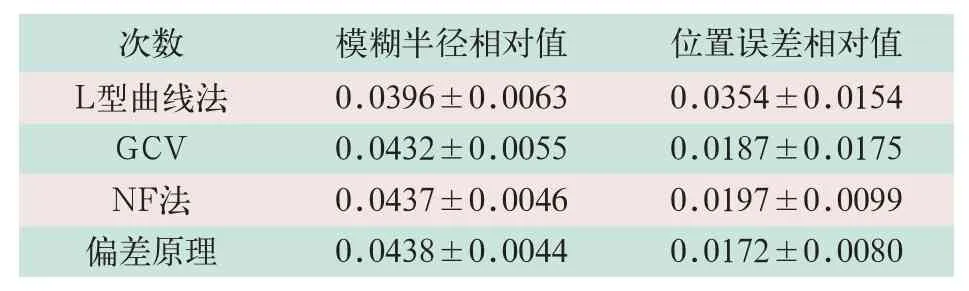
表1 添加50次不同的0.1%高斯白噪声的不同方法的统计结果
6 讨论
脑部电阻抗图像重建曾经使用的是固定正则参数的方法,该方法已不适应实时最优化图像的需要。图1结合图3说明,在正则参数α很小时,‖Axα-y‖很小,说明xα逼近了真实解,但是‖xα‖很大,说明解是不稳定的;当正则参数α较大时,‖xα‖很小,表明解是稳定的,但是‖Axα-y‖很大时则表明xα与真实解相去甚远。最优的正则化参数必须同时兼顾解的“精确性”和“稳定性”。为此,本研究在含高阻抗颅骨的颅脑模型中,量化比较了4种正则化参数选取方法:L型曲线法、广义交叉校验法、固定噪声系数法和偏差原理法,希望找到一种适用于脑部EIT的选取正则参数的算法。
(1)L型曲线法:统计结果表明,虽然L型曲线法取得了最小的模糊半径,但L型曲线法重建所得的目标位置误差比较大,达到0.0354±0.0154,表明L型曲线法重建目标位置不准确;此外,当边界电压噪声较大时,曲线并不呈现明显的L型,而是变得扁平,在这种情况下曲线法求出的拐点并不准确甚至无法求得拐点,即无法求得最优的正则参数。
(2)广义交叉校验法:广义交叉校验法重建所得的目标位置误差为0.0187±0.0175,位置误差的均方差较大,表明通过该方法重建目标的位置不稳定。Graham等[11]的研究亦表明,GCV方法在电阻抗断层成像中不可靠。
(3)固定噪声系数法:本研究中在使用固定噪声系数法取NF=0.5时取得了较好的成像结果。该方法提供了一种新的选取正则参数的方法,可重复性好,并且比L型曲线法、GCV方法更稳定,但是不同的NF取值会对重建图像结果有较大影响,而NF取值存在很大的主观因素。因此,固定噪声系数法不够客观。
(4)偏差原理法:偏差原理法结果较好,模糊半径处于合理水平,且多次成像位置误差小,位置误差的方差较小,成像结果稳定,是较好的正则参数选取方法。
研究显示,偏差原理法成像效果比较依赖对于误差的估计,目前一般采用先采集一段数据,然后根据预采集数据来估计误差,但这种方法有一定的局限性;此外,重建模型的剖分规模的增大,会导致偏差原理法耗时指数式增长。因此,提高误差估计精确性和利用更快的迭代算法加快偏差原理法的运行速度有待进一步研究。
7 结论
本研究通过统计比较4种选取正则参数的方法得出结论:偏差原理法取得了最好的结果,重建图像的结果最客观、最稳定和最接近真实解,可采用偏差原理法作为脑部EIT正则参数的选取算法。
[1]董秀珍.生物电阻抗成像研究的现状与挑战[J].中国生物医学工程年报,2008,27(5):641-643.
[2]史学涛,霍旭阳,尤富生,等.颅内出血电阻抗成像系统及初步动物实验[J].航天医学与医学工程,2007,20(1):24-27.
[3]刘丽旭,董为伟,贾建平,等.无创性脑电阻抗测定在脑出血患者脑水肿监测中的应用[J].中华神经科杂志,2007,40(6):383-386.
[4]Dai M,Wang L,Xu C,et al.Real-time imaging of subarachnoid hemorrhage in piglets with electrical impedance tomography[J].Physiol Meas,2010,31(9):1229-1239.
[5]Xu C,Dai M,You F,et al.An optimized strategy for real-time hemorrhage monitoring with electrical impedance tomography[J].Physiol Meas,2011,32(5):585-598.
[6]Dai M,Li B,Hu S,et al.In vivo imaging of twist drill drainage for subdural hematoma:a clinical feasibility study on electrical impedance tomography for measuring intracranial bleeding in humans[J].PloS One,2013,8(1):e55020.
[7]倪安胜,杨国胜,付峰,等.基于非均匀颅骨头模型的电阻抗断层成像图像重构[J].航天医学与医学工程,2008,21(1):56-60.
[8]Sadleir RJ,Argibay A.Modeling skull electrical properties[J].Ann Biomed Eng,2007,35(10):1699-1712.
[9]Tang C,You F,Cheng G,et al.Modeling the frequency dependence of the electrical properties of the live human skull[J].Physiol Meas,2009,30(12):1293-1301.
[10]Vauhkonen M,Vadász D,Karjalainen PA,et al.Tikhonov regularization and prior information in electrical impedance tomography[J].IEEE Trans Med Imaging,1998,17(2):285-293.
[11]Graham BM,Adler A.Objective selection of hyperparameter for EIT[J].Physiol Meas,2006,27(5):S65-S79.
[12]Abascal JF,Arridge SR,Bayford RH,et al.Comparison of methods for optimal choice of the regularization parameter for linear electrical impedance tomography of brain function[J].Physiol Meas,2008,29(11):1319-1334.
[13]Adler A,Dai T,Lionheart WR.Temporal image reconstruction in electrical impedance tomography[J].Physiol Meas,2007,28(7):S1-S11.
[14]Adler A,Guardo R.Electrical impedance tomography:regularized imaging and contrast detection[J].IEEE Trans Med Imaging,1996,15(2):170-179.
[15]Wang Y,Xiao T.Fast realization algorithms for determining regularization parameters in linear inverse problems[J].Inverse problems,2001,17(2):281-291.