对自动分析仪 “样本携带污染率”测试方法的探讨

2013-09-12刘彤戴长生张少波孙旭东上海润达医疗科技股份有限公司上海201106

中国医疗器械信息 2013年2期

刘彤戴长生张少波孙旭东上海润达医疗科技股份有限公司（上海 201106）

在测试评价自动分析仪的性能中，有一项重要的技术指标就是“样本携带污染率”。我公司最近在起草几个自动分析仪器的企业标准时，对“样本携带污染率”采用什么方法测试、使用什么公式，有不同的意见，为此我们进行了一番探讨，现将我们探讨的结果发表，抛砖引玉，请各位专家、学者和同行给予指导。

1.某分析仪“样本携带污染率”测试方法

连续测定正常浓度血液样本（某物资含量应在4.0%～6%范围内）4次，结果记为（a1、a2、a3、a4）后，立即连续测定高值血液样本（某物资含量应≥12.0%）4次（b1、b2、b3、b4），再连续测定原正常浓度血液样本1次（a5、），根据公式计算样本携带污染率K（%）。

2. “样本携带污染率”的计算公式

提出的计算公式有三个：

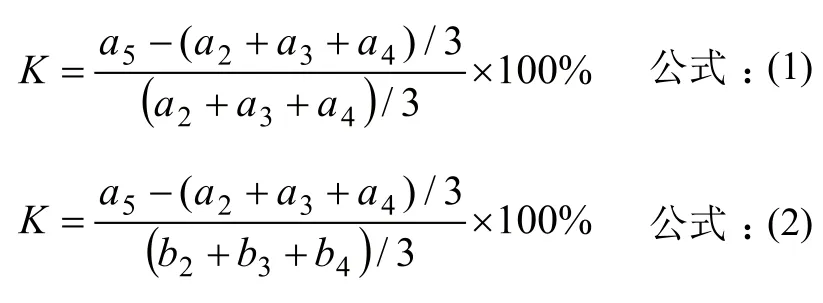
公式中，（a2、a3、a4）和（b2、b3、b4）求均值是为了排除仪器测试时产生的随机误差。

3.样本携带污染率 K 的计算公式的分析

从公式 1 来看，计算出来的 “样本携带污染率”，实际上是“测量高值样本后再测试低值样本，测试值的相对偏差”，没有考虑“高值样本与低值样本的差值”，从多次试验的结果来看，计算出来的值与前后两个样本含量的差值关系很大，如果两个样本的差值小，样本携带污染率K就比较小，反之，K就比较大。K不是一个常数。不利于对一个仪器做出有统一标准的评价，如果要做出有统一标准的评价，必须指定高值样本和低值样本的值，但这样，在实验时不易得到指定值的样本，必须先测试样本的值后，再配制出指定值的样本，使测试工作变得很复杂。

从公式 2 来看,分母采用高值的平均值，考虑了高值样本的影响，但并没有考虑二者的差值，计算出来的值也不是一个常数，由于应用不多，我们这里就不深入讨论。

公式 3 首先是1984年由英国伊莉莎白皇后医学中心 Wolfson 研究实验室，P.M.G.Broughton 先生提出，他在《自动化学杂志》第六卷（《Journal of Automatic Chemistry》Volume 6,Number 2(April-June 1984), Pages 94-95 P.M.G.Broughton）发表了“自动分析仪的携带污染”的论文，对自动分析仪的“样本携带污染率”进行了科学的分析，并推荐了测试方法和计算公式，他提出来的测试方法和公式是：

对同一个高浓度的分析物测试2次，结果记为a1和a2；接着对同一个低浓度的分析物测试2次，结果记为b1和b2，携带污染(k)的计算公式为：

在这个公式中，假定测试值是没有仪器测试的随机误差的。

之后这个计算公式被众多著名实验室应用，并在许多标准中应用，如：《YY/T 0014-2005半自动生化分析仪》、《YY-T 0653-2008 血液分析仪》等，为了排除仪器测试的随机误差，a2和b2都采用测试值的均值。

4.对公式（4）进行数学分析

我们通过如下运算，发现了公式4中计算出来的 K 值的具体含义。

设，某仪器的测试目的是检测血液中H物质的含量百分比。

设，第一个样本a，H 物质的含量值为Ca%，第二个样本b，H 物质的含量值为Cb%，自动仪器测试一个样本a后，经过清洗，该样本在整个对测试结果有影响的部位残留物体积与第二个样本混合后的总体积之比为Va，总体积为1，下一个样本b在混合后的总体积中占比为（1-Va）；

一般自动化分析仪器中分析一个样本a后，经过冲洗，再分析下一个样本b两次，b样本的第一次测试值会受到上一个样本的残留影响，但第二次测试值的残留影响可以忽略不计，

则：a2=Ca% ，b2=Cb%

设，第二个样本 b 与第一个样本a的残留物混合后的值为Cab%，则：

按公式 4 求出“样本携带污染率 K”

把a2、b2和公式5代入公式4：

分子和分母都乘以100

合并同类项得

提取公因式后

约分后K=Va

化成百分数：K=Va*100%

由此可得出，根据该公式 4 求出来的样本携带污染率K，是自动分析仪内部上一个样本的残留量相对于下一个样本的输入量加上一个样本的残留量的总体积比。

上述公式运算，排除了自动分析仪测试产生的随机偏差，结果是准确可靠的。

显然，影响“样本携带污染率K”的因数主要是清洗条件，清洗剂的清洗能力、用量、清洗次数、清洗温度、搅拌条件等，在自动分析仪中，清洗条件恒定不变的情况下，“样本携带污染率 K”是一个不随样本含量和相邻两个样本含量差值的影响的一个常数。我们认为用这个值来评价自动分析仪器的样本携带污染率是最合适的。

在自动化的分析仪器，要将“样本携带污染率K”降低到一个非常低的值，只要多用一些试剂，多冲洗几次，是不难做到的。但分析仪的制造商必须兼顾单个分析样本的时间，即仪器分析效率，尽量减少清洗分析仪所需的试剂消耗等，一般都是将其控制在一个可接受的性价比范围内。

5.根据第二个样本测试值求出第二个样本的真值

如果已知第一个样本a和第二个样本b的真值和仪器的样本携带污染率K，可以计算出第二个样本b的测试值，也可以根据样本 b 的测试值求出样本b的真值。

如果在具有计算机软件的自动分析仪上，利用公式 6 去修正测试值，用修正值报告结果，理论上可使“样本携带污染”带来的相对偏差为零。

实际应用时，测试b1，本身有随机偏差，a2也有随机偏差，由于K值一般小于2%，如果测试随机偏差的最大值是 5%，我们来计算a2带来的最大随机偏差：

可见，由a2带来的随机偏差为0.102%，与测试随机偏差的最大值是5%相比，可以忽略不计。

因此，对于自动化分析仪器的制造商而言，在进一步提高清洗效果时间太长影响分析效率或成本太高的情况下，使用公式（6）去修正测试数据，是降低“样本携带污染率”的一个办法。

理论上，只要 K 值精确，仪器测试的线性很好，使用公式（6）可以准确的校准由“样本携带污染率”带来的误差。但是，由于自动化分析仪分辨率不足或线性不太好时，在自动化分析仪中对于前后两个样本差值特别大的情况下，使用公式得到的值与样本真值可能会有一些偏差，但比校正前的数据准确度仍会有很大的提高。

由于不同的仪器的线性范围和线性特征不同，如果通过多次实验，在公式（6）的基础上，求出能符合该仪器的校正函数，可使校正值更准确。

对于自动化分析仪器的使用者而言，为了使测试值更准确，在知道测试仪器的样本携带污染率K的情况下，也可以用 Excel 建立表格，把测试值导入表格中，使用公式（6）计算出测试的修正值，在批量测试中，当前后两个样本含量差距较大时，有积极的意义。

6.样本携带污染率的数学分析表

根据上述分析，我们可以根据公式 (5) 求出被测试样本经过自动分析仪的携带污染后的测试值，下面我们按以下规律用 Excel建立表格：

a) 设：仪器内部样本残留量占混合样本的比例为1.5%、2.0%；

b) 将样本真值0.30—7.00（RBC单位：1012/L）之间取一些代表性的值填入表中；

c) 按公式（5）Cb%=(Cab%-Ca%*Va)/(1-Va)计算经过携带污染后的理论值（即前一个样本残留量与后一个样本吸取量混合后的理论值）；

d) 求出绝对偏差；

e) 按公式 (b1-b2）/b2计算相对偏差；

f) 按公式（3）以混合后的理论值作为b1，真值分别为a2、b2，计算“样本携带污染率”K=(b1-b2)/（a2-b2）；

表1. 某血液分析仪 RBC“ 样本携带污染率”的理论分析表（RBC单位：1012/L）

g) 按公式（6）求出样本修正后的值；h) 计算修正后的“样本携带污染率” K ；

i) 为了使数据精确，样本真值采用了4位小数，混合后理论值采用了6位小数。

由表1可见：

a) 前一个样本与后一个样本的差值越大，相对偏差也越大（见 1、2、3 和 13、14、15 行内的值），当二者相等时，相对偏差为零（见10、11和22、23 行内的值）。

b) 前一个样本比第二个样本值高时，相对偏差是正值，前一个样本比第二个样本值低时，相对偏差是负值。（见1、2、3和13、14、15 行内的值）

c) 前一个样本对后一个样本的污染，“高值样本对低值样本的污染率K”与“低值样本对高值样本的污染率K”都是一样的（见1、2、3和13、14、15 行内的值）。

d) 前一个样本比第二个样本值高时，两者差值很大时，相对偏差大，当相同的两个样本改变测试顺序时，绝对偏差的绝对值相等，因计算相对偏差采用的分母不一样，所以相对偏差小，并且相对偏差是负值（见表一见1、2、3和13、14、15 行内的值）。

e) 前一个样本对后一个样本的污染率，不管高值、低值和两者之间的差值大小，计算出来的K值是一样的。K值与仪器内部样本残留量占混合样本的比例相等。

f) 当前后两个样本相等时，但是，因为此时分子和分母都为零，计算会出错。所以，表内有几个数据采用4位小数，并使其值相差0.0001 （见10、11和22、23行内的值）计算出来的K值也是一样的。

g) 根据前一个样本的真值和第二个样本的测试值，使用公式（6）可求出第二个样本的真值，理论上可使报告值的相对偏差和样本携带污染率为零。

因此，在自动化分析仪中，当进一步降低样本携带污染率K的成本太高时，可以考虑使用数学公式（6），将测试值换算出该样本的真值。尤其是前面样本某物资含量高于其后的样本数倍时，修正后的数值准确度大大提高。

7.测试“样本携带污染率”必须排除自动分析仪的随机偏差

很多标准和规范给出的求样本携带污染率 K的方法都是：

连续测定正常浓度血液样本（某物资含量应在4.0%～6%范围内）4次，结果记为（a1、a2、a3、a4）后，立即连续测定高值血液样本（某物资含量应≥ 12.0%）4 次（b1、b2、b3、b4），再连续测定原正常浓度血液样本1次（a5），根据公式计算样本携带污染率。

然后利用公式（3）计算 K

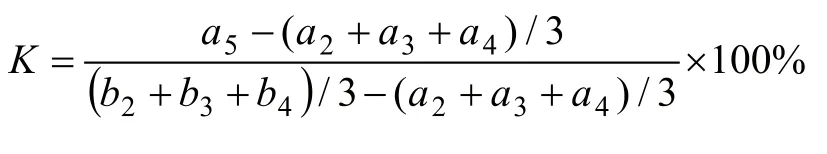
我们知道，任何检验仪器，都存在着测试随机偏差，而医疗检测仪器测试的随机偏差还比较大，正常情况下，测试值是可能出现正偏差和负偏差。上述方法中，a5只测一次，而其他值都取3次测试值的均值，这样就可能出现一些不正确的结果。

我们使用某自动分析仪做重复性实验，用同一个样本连续测21次，第一次测的数据不用，其余20个数据如表二，我们用这一组数据来分析计算 K 的几种可能性。

表2.

该自动分析仪的行业标准CV值的要求是≤3.0%，该组数据的CV值为 1.63%，是一组随机偏差比较小的数据。

设样本 b 的平均值为 7.00，在实际测试过程中，会有很多种排列组合，这里，我们考虑极限值的组合情况，可能会有如下排列和组合，我们将其数值填入表（3）：

1) 第一种极限情况，最大值与最小值，设a5是表（2）中选取最大的数，a2、a3、a4取表（2）中最小的连续三个数，来计算K，如表（3）1 行。

2) 第二种极限情况，最小值与最大值，设a5是表（2）中选取最小的数，a2、a3、a4取表（2）中最大的连续三个数，来计算 K，如表（3）2 行。

3) 最大值与最大值，选择表（2）内都偏大的一组数据，如表（3）3 行。

4) 最小值与最小值，选择表（2）内都偏小的一组数据，如表（3）4 行。

5) 最大值与中间值，选择表（2）内最大值与接近于平均值的一组数据，如表（3）第 5 行。

6) 中间值与中间值，选择表（2）内都接近于平均值的一组数据，如表（3）第 6 行。

7) 中间值与最大值，选择表（2）内中间值与最大值的一组数据，如表（3）第 7 行。

从表（3）可以看出，只有最大值与最大值、最小值与最小值、中间值与中间值计算出来的携带污染率符合要求，

在这些测试的数据里，是对同一个样本重复测试，实际上并没有高值样本对低值样本产生的携带污染，仅仅仪器的随机偏差计算出来的 K 值和相对偏差就有如此大的差异。

高值样本对低值样本产生的样本携带污染率和的相对偏差应该为正值，但在第二种假设情况下，高值样本对低值样本竟产生了负的样本携带污染率和负的相对偏差。这在理论上是说不通的。

按这种测试方法，对自动分析仪做样本携带污染率测试，可能随机偏差的测试值掩盖了仪器本身的“样本携带污染率”的概率很高，得出的结果难以对自动分析仪做出正确的评价。

因此，要正确测试自动分析仪器的样本携带污染率，必须排除仪器的随机偏差，我们认为，计算“样本携带污染率”K值，所有运算的测试值都必须采用均值。

我们建议的测试方法为：

使用低值和高值的样本进行测试，高值样本和低值样本的差值应足够大，并在仪器分辨率比较灵敏的范围，（根据测试仪器和测试样本的不同，在产品标准或检验规范中，可以对样本的取值范围和差值范围提出建议）先测试高值样本一次，测试值不计，接着低值样本测试两次，然后测试高值样本两次，这样重复3～5次（或更多次），低值样本分别记为，a1～a10 ，高值样本分别记为b1～b10，如果存在携带污染，则奇数测试值a1～a9是被高值样本污染的测试值，偶数测试值a2～a10是没有被污染的低值样本测试值，偶数测试值b2～b10是没有被污染的高值样本测试值。

我们建议的计算公式为：