平头钢弹侵彻钢靶板过载特性的数值分析

卢玉斌，程永生，孙远程

(1.中国工程物理研究院电子工程研究所，四川 绵阳 621900;2.西南科技大学制造过程测试技术教育部重点实验室，四川 绵阳 621010)

现代战争要求弹丸材料的力学性能、战斗部引信和装药的安定性必须满足高过载要求。其中，引信的过载特性最重要，一方面引信强度必须能承受高过载;另一方面，为了实现弹药在最佳炸深爆炸，引信的延时要与侵彻行程相互协调，而所有这些工作都建立在对侵彻过程中弹体过载特性的准确认识基础上，所以对弹体侵彻过程中过载特性的研究就很重要［1-3］。

由于目标介质的多样性和实验条件的复杂性，使得研究硬目标侵彻过载特性存在较大困难。到目前为止，对不同介质侵彻过载的研究主要有两种方法:① 实验研究，随着实验技术的发展，可用弹内存贮技术来记录弹丸侵彻介质时的过载曲线;②数值仿真，目前已经有一些大型商用软件可以用来计算侵彻过程，如LS-DYNA、Autodyn、Dytran等。数值计算可使侵彻过程可视化，得到大量的时间变量，增加对侵彻机理的理解［4］。

文献［5］指出，侵彻过载随时间的变化规律与弹丸的着速、着角、结构参数以及靶板厚度等因素有关。本文对平头钢弹侵钢靶板的过载特性进行了数值模拟，分析了弹体的长径比、弹体着速、弹体结构响应等因素对弹丸过载特性的影响。

1 有限元计算模型

根据穿甲工程力学的理论［6］，仿真模型的建立基于如下基本假设:弹丸和靶板为均匀连续介质;整个侵彻冲击过程为绝热过程，不计空气阻力，不考虑重力的作用，不考虑靶板的侧边效应，忽略靶板的整体运动;弹丸和靶板的初始应力为零。

为了说明弹体着速、长径比及刚体假设等对侵彻过载特性的影响，本文弹体与靶板采用相同的材料，均为4043钢，从而可以不考虑材料的影响。在有限元模拟中，采用LSDYNA有限元软件，为了降低计算规模和节省计算时间，取1/4模型进行分析，设置非反射边界和对称边界。靶板的长和宽为800 mm、厚度为10 mm，弹体直径均为40 mm。采用Johnson-cook本构模型［7］，材料主要参数如表 1所示［8］，参考应变率取为1 s-1，参考室温取为20℃。对于模型中材料失效参数的取值，D2～D5均取为0，然后对D1进行参数敏感性分析，通过比较由数值模拟获得的剩余速度确定出D1=1.9。然后进行网格敏感性分析，并比较弹体的剩余速度，发现当弹体的总体网格尺寸取为2 mm，靶体长和宽划分50份(Bias factor设置为2)、厚度划分4份时能够兼顾计算精度和时间。已划分网格的有限元模型如图1所示。

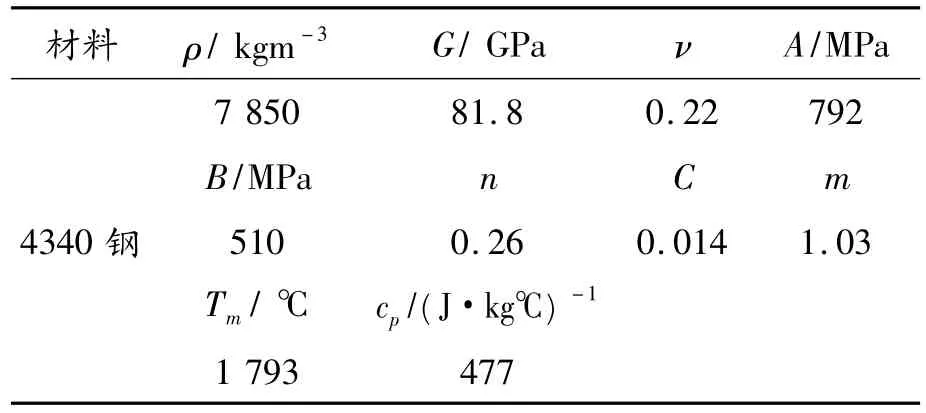
表1 材料主要参数［8］

图1 划分网格的有限元模型

2 数值模拟结果及分析

当弹体长度为500 mm(长径比为12.5)、弹体速度为470 m/s时，靶板尚没有贯穿。弹体前端、质心、后端位置处的过载时间曲线如图2所示。由图2可知，撞击前端处的过载峰值极高、脉宽较窄，而质心和后端位置处的过载峰值已大大降低，且脉宽变长。从质心到后端位置的一系列节点处的过载曲线可以看出，靠近后端节点处的过载曲线较为平滑，过载峰值较低，且存在一个节点位置处的过载第一峰值最低，该节点距离后端面为48 mm。由有限元模拟结果直接得到的弹体上的刚体过载曲线如图3所示，其过载峰值相较耦合了应力波响应的弹体质心处原始过载曲线(图2)的峰值要低。弹体上不同位置处的应力-时间曲线如图4所示，由图可知，靠近弹体前端位置处的应力波以塑性应力波为主，随着单元位置逐渐向弹体后端变化，应力波逐渐转变为弹性应力波，且在过载峰值最低处，由于压缩波和反射拉伸波的叠加，导致该处应力波的峰值最小，应力波曲线较为光滑。

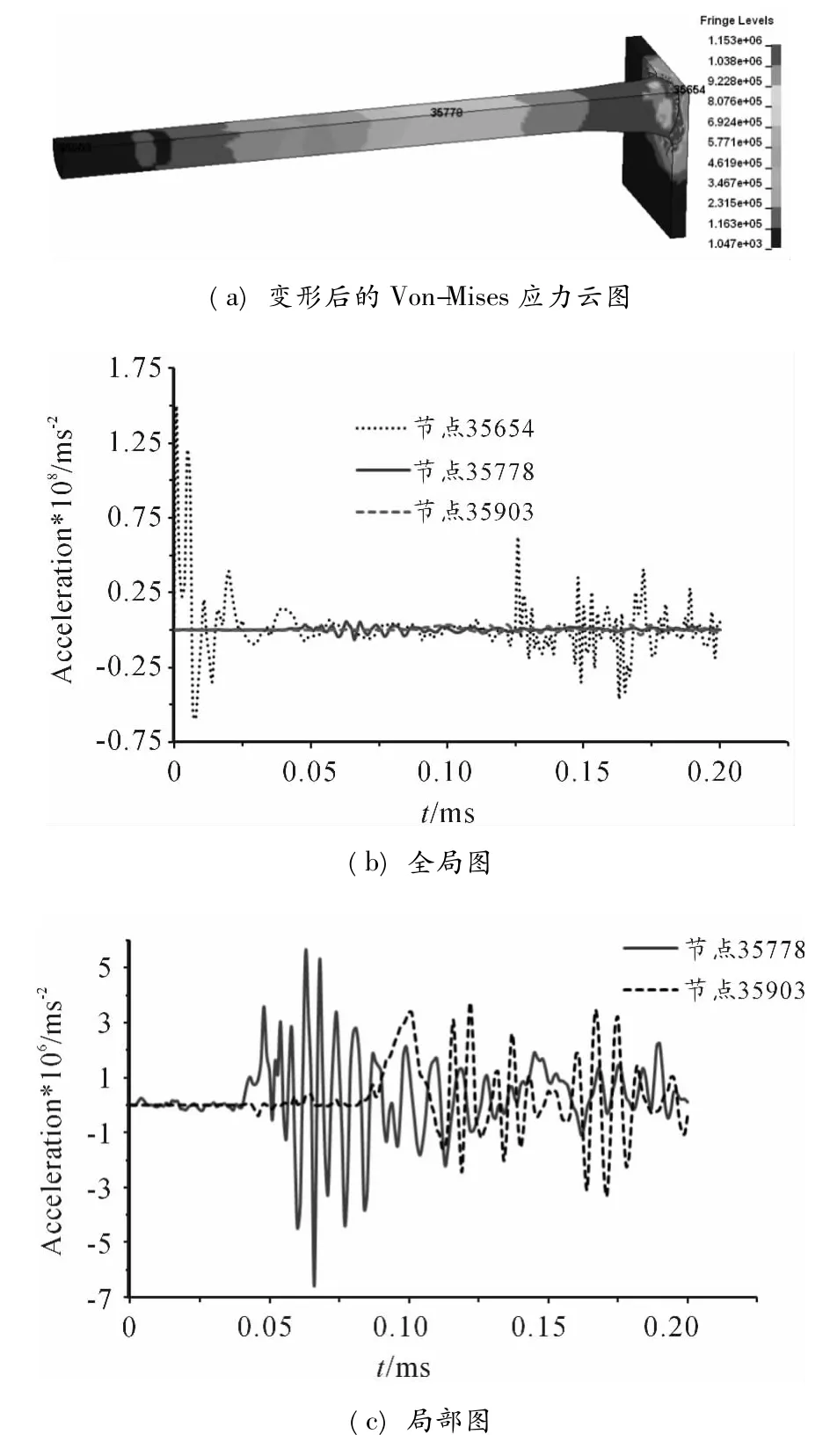
图2 弹体前端、质心、后端的过载曲线，v=470 m/s，l/d=12.5

当弹体速度增加到800 m/s时，靶板已被完全贯穿。与弹体速度v为470 m/s时的刚体过载曲线相比，v为800 m/s时的刚体过载峰值增加，约为前者的1.7倍，与弹体速度的比值相当。由弹体上不同位置处的过载曲线结果发现当弹体速度增加时，前端和质心处的过载曲线上的峰值增加，而后端的过载曲线上的峰值降低。过载第一峰值最小的节点距离后端面为44 mm。

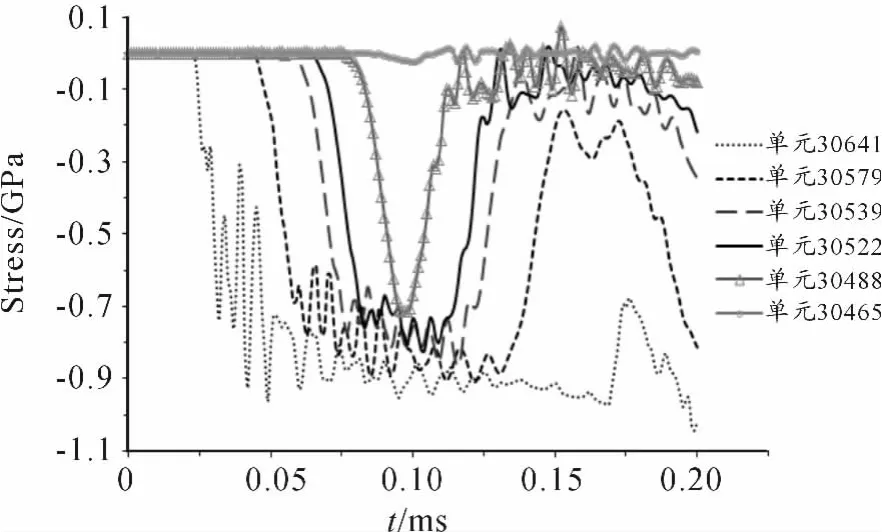
图4 弹体上不同位置处的应力波曲线，v=470 m/s，l/d=12.5

为了进行对比，在有限元模拟中将弹体设置为刚体进行了分析。当弹体速度v=470 m/s时，弹体上不同节点处的刚体过载曲线如图5所示。由图5可知，其过载峰值与将弹体考虑为弹塑性变形体时的相比，约为前者(图3)的3.43倍。并且已将靶体贯穿。

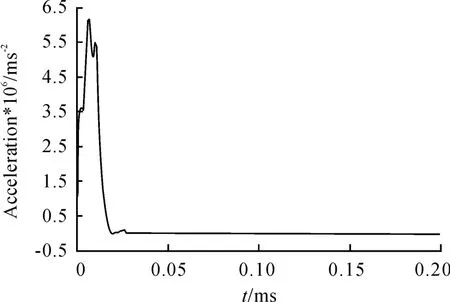
图5 弹体为刚体时的过载曲线，v=470 m/s，l/d=12.5

当弹体的长径比缩短为5时，不同弹体速度时弹体上的刚体过载曲线如图6所示。弹体速度v=470 m/s和v=800 m/s与v=130 m/s时弹体速度的比值分别约为3.6倍和6.1倍，刚体过载曲线上过载峰值的比值则分别约为2.7倍和5.0倍，同时可发现刚体过载趋于0值所需的时间基本随着弹体速度的增加而减少。与弹体长径比为10时相比，在相同的弹体速度下(v=470 m/s、800 m/s)，刚体过载分别为前者的2.57倍和2.67倍。不同弹体速度时弹体前端、质心、后端位置处的过载时间曲线结果表明，随着弹体速度的增加，前端的过载曲线上的峰值随之增加，后端的过载曲线上的第一个峰值随之降低，而质心处过载曲线上的第一个峰值先增后降。不同弹体速度时弹体上不同节点处的过载曲线结果表明，同样存在一个靠近后端面的节点位置，该处过载的第一个峰值最小，对应于 v=130 m/s、470 m/s、800 m/s，该节点与后端面的距离分别为34 mm、4 mm、12 mm，呈现先降后增的趋势。

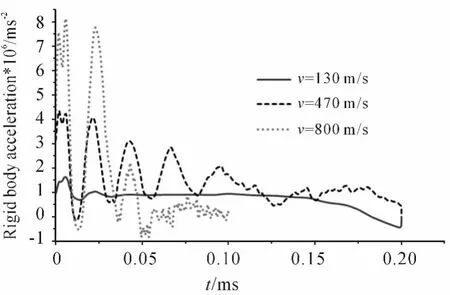
图6 弹体上的刚体过载曲线，l/d=5

当弹体的长径比进一步缩短为1.5时，不同弹体速度时弹体上的刚体过载曲线如图7所示。弹体速度v=1000 m/s和v=800 m/s与v=470 m/s时弹体速度的比值分别约为2.1倍和1.7倍，刚体过载曲线上加速度峰值的比值则分别约为2.6倍和1.8倍。与弹体长径比为5时相比，在相同的弹体速度下(v=470 m/s、800 m/s)，刚体过载分别为前者的3.3倍和3.4倍。不同弹体速度时弹体上不同节点处的过载曲线结果显示，同样存在一个靠近后端面的节点位置，该处过载的第一个峰值最小，对应于v=470 m/s、800 m/s、1000 m/s，该节点与后端面的距离分别为4 mm、6 mm、6 mm。

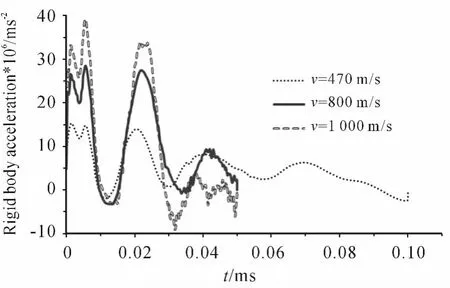
图7 弹体上的刚体加速度曲线，l/d=1.5

不同长径比、弹体速度以及将弹体设置为刚体时的质心和后端处过载曲线的第一峰值、以及弹体上某处过载曲线第一峰值最小时与后端面的距离总结在表2中。通过表2中的数据可得到前述关于侵彻过载的变化规律。

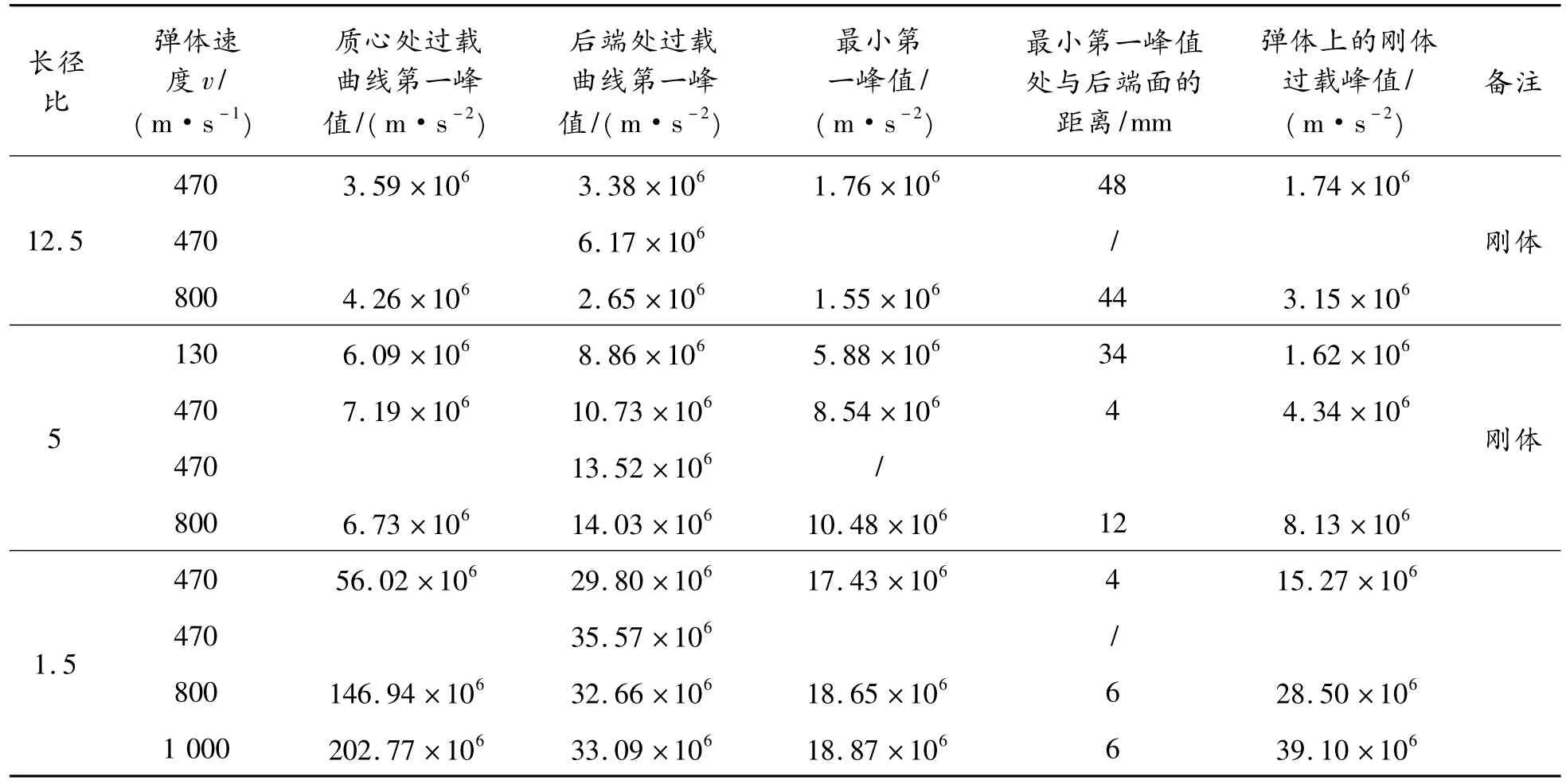
表2 不同条件时过载峰值总结

3 结论

通过对具有不同的着靶速度和长径比的钢质平头弹体侵彻钢靶板的仿真，分析了弹体过载的变化情况，得到如下结论:

(1)靠近弹体后端节点处的过载曲线较为平滑，过载峰值较低，且存在一个节点位置处的过载第一峰值最低，该节点与后端面的距离和弹体的长径比及弹体的入靶速度均有关系，变化范围为4～48 mm。

(2)靠近弹体前端位置处的应力波以塑性应力波为主，随着单元位置逐渐向弹体后端变化，应力波逐渐转变为弹性应力波，且在过载峰值最低处，由于压缩波和反射拉伸波的叠加，导致该处应力波的峰值最小，应力波曲线较为光滑。

(3)由有限元模拟结果直接得到的弹体上的刚体过载曲线的过载峰值相较弹体质心处的原始过载曲线的峰值要低，说明原始过载曲线中耦合了应力波响应的影响。

(4)弹体长径比相同时，随着弹体入靶速度的增加，弹体上的刚体过载曲线的过载峰值随之增加，侵彻深度同样增加;当弹体入靶速度相同时，随着弹体长径比的减小，弹体上的刚体过载曲线的过载峰值随之增加，侵彻深度随之降低。

(5)把弹体设置为刚体得到的过载曲线的过载峰值与将弹体考虑为弹塑性变形体时弹体上的刚体过载曲线的加速度峰值相比，约为后者的好几倍，前者的侵彻深度也较大。

［1］刘璞，施坤林，黄惠东.钢板侵彻过载的三维数值模拟［J］.探测与控制学报，2006，28(1)：25-28.

［2］刘立军，祖静，范锦彪，等.动能子弹侵彻钢板加速度测试与分析［J］.传感器与微系统，2010，29(6)：15-17.

［3］Zhang W，Cheng L J，Xiong J J，et al.Ultra-high g deceleration-time measurement for the penetration into steel target［J］.International Journal of Impact Engineering，2007，34(3)：436-447.

［4］刘伟钊，陈侃，李蓉，等.不同介质侵彻过载特征参量有限元仿真方法［J］.科学技术与工程，2011，11(5)：3494-3497，3500.

［5］屈新芬，商顺昌，杨晴.影响弹丸侵彻性能的因素分析及引信方案探讨［J］.信息与电子工程，2003，1(3)：51-55.

［6］赵国志.穿甲工程力学［M］.北京：兵器工业出版社，1992：106-107.

［7］LivermoresoftwareTechnologyCorporation. LS-DYNA Keyword User’s Manual(970v)［Z］.Livermore，2003.

［8］张清爽.弹丸侵彻装甲钢板过载特性数值模拟［J］.弹箭与制导学报，2009，29(4)：133-135.

［9］张迪.扩展有限元法在弹靶侵彻中的应用［J］.重庆理工大学学报：自然科学版，2012(5)：43-46.