履带张紧力对火炮炮口扰动影响研究
2013-09-12韩小平
韩小平,王 炎
(1.装甲兵工程学院,北京 100072;2.66064部队,山西 忻州 034000)
射击精度是火炮的主要性能指标,弹丸的起始扰动是影响射击精度的主要因素,因此,揭示在弹丸出炮口前,火炮的运动和动力关系对于提高火炮的射击精度有重要运用价值。许多学者在这方面进行了深入的研究,曾晋春等考虑了高低机齿轮齿弧的接触/碰撞作用对炮口扰动的影响[1];刘雷、葛建立等研究了弹丸与身管的耦合作用对炮口扰动的影响[2,3]。履带作为自行火炮的一部分,必然会对火炮的运动产生影响,目前还没有研究履带张紧力对火炮运动及射击精度影响的公开文献。
在工程上认为,弹丸出炮口前属于半约束期,由于其作用时间很短,通常只有十几毫秒,且射击时履带张紧、主动轮制动,在进行火炮动力学计算时,一般将履带系统进行简化[4]。但履带式自行火炮的履带使车体的线位移和角位移相互关联,使火炮在封闭的履带中做后坐运动,将会对火炮的运动产生影响[5]。另外,履带张紧力的大小影响了负重轮的初始位置,使火炮的初始状态发生了变化,有必要建立完整履带系统的发射动力学模型,研究张紧力的大小对膛内运动时期火炮动力学的影响。
1 履带对火炮运动的影响分析
如图1所示,射击过程中,诱导轮闭锁,诱导轮中心与车体之间无相对平动,只有相对转动,诱导轮上的履带板可以绕诱导轮回转中心转动。后坐部分在炮膛合力作用下,开始后坐运动,同时车体也产生向后的运动。由于主动轮制动,主动轮与车体无相对运动,并且履带与地面之间存在很大的摩擦力而与地面无相对滑动,使具有悬挂的车体产生车尾向下的回转运动。由于车体产生后坐运动,一方面,主动轮与第一负重轮之间的距离缩短,使原来张紧的履带部分得到解脱;另一方面,诱导轮与第六负重之间的距离被拉大,使履带张紧力进一步加大。

图1 力学模型与坐标系
2 动力学分析
为了分析的方便,假设火炮是一个对称体,后坐部分的作用力都在对称轴上,这样将立体的问题转化成了平面问题。整个火炮系统分为后坐部分、起落部分(不含后坐部分)、车体共3个刚体。
惯性系的坐标如图1所示,其原点位于车体质心处,取系统的广义坐标为:q={q1,q2,q3,q4,q5}T,其中:q1为车体水平坐标;q2为车体的垂直坐标;q3为车体绕质心的转角,逆时针为正;q4为起落部分的俯仰角,逆时针为正;q5为后坐部分的位移,向后为正。由达朗伯原理:
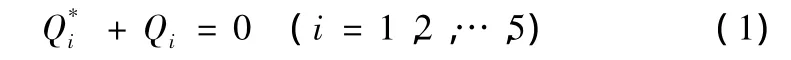
对于第一个广义坐标q1,其所受到的广义主动力:

式(2)中:q40为第4个广义坐标的初始值,亦即火炮的初始射角;T为履带张紧力;F为负重轮在履带上的滚动摩擦阻力;Fpt为炮膛合力。
受到的广义惯性力:
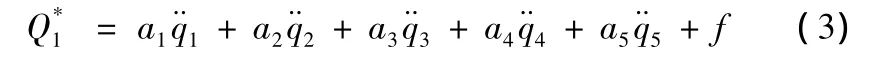
式(3)中:等式右边的第1部分为q1方向的惯性力;第2~5部分为q2~q5方向惯性力在q1方向的分量,当火炮的位置状态确定后,a1~a5的值唯一确定,由于q1、q2垂直,a2=0;f-牵连运动产生的科氏惯性力在q1方向的分量。(为了与后面的等式有相同的形式,将力与力矩写成一个等式,对于力的平衡则力矩前面的系数取0,对于力矩的平衡通过乘以力臂建立平衡关系)。
将式(2)、式(3)代入式(1),得到第一个方程,其他4个广义坐标也可依据达朗伯原理建立方程。这样就得到5个方程,由于广义主动力中履带张紧力T未知,还需要补充一个约束方程。
履带使得车体的线位移和角位移相互关联,据此建立约束方程:

这样由6个方程求解6个未知量,可以得到封闭解,在方程中含有履带张紧力,显然履带张紧力会对火炮的运动产生影响。
3 建模分析
随着计算机技术和动力学软件的发展,基于虚拟样机技术,以某自行火炮为研究对象,建立含履带板之间相互作用的三维实体仿真模型,模拟履带系统在不同张紧力下,对火炮炮口扰动的影响。
履带板之间以旋转铰相连,首尾履带板用高刚度的弹簧连接;火炮在硬质地面射击,定义下侧、前后两端履带板与地面的接触;主动轮、诱导轮和负重轮与履带板之间的作用以接触定义,只定义那些有可能产生接触的履带板,用一个Motion=0的角速度约束来模拟主动轮的制动;第2~4负重轮以线性弹簧阻尼器模拟扭力轴的作用;第1、6负重轮以非线性弹簧阻尼器模拟液气悬挂的作用;分别以一个弹簧阻尼器模拟高低机、方向机、平衡机的作用;复进机、制退机力分别是其广义坐标和广义速度的函数,分别用一个双向力来模拟后坐部分与摇架的相互作用;将炮膛合力以样条函数的形式施加于炮尾。其拓扑结构如图2所示,整个模型有198个刚体,189个自由度。
4 结果分析
射击条件:常温、底凹弹、0°射向、0°射角、主动轮制动、硬质地面,以炮口中心点的运动情况为研究对象。坐标系如图1所示,运动参考点为地面上距车体正后方0.5 m处。图中曲线1、2、3、4 的分别代表履带张紧力为 3e4N、2.45e4 N、2.25e4 N、2e4 N。炮口点的位移、角速度曲线如图3、4所示。
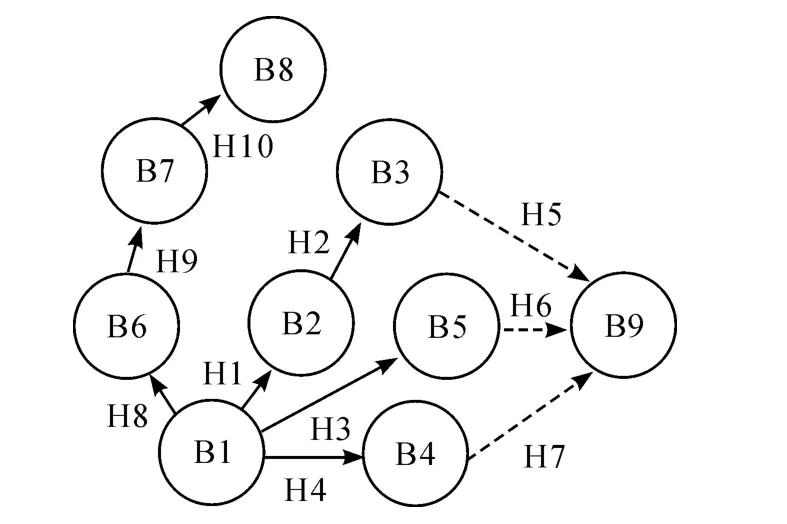
图2 履带式火炮的拓扑结构
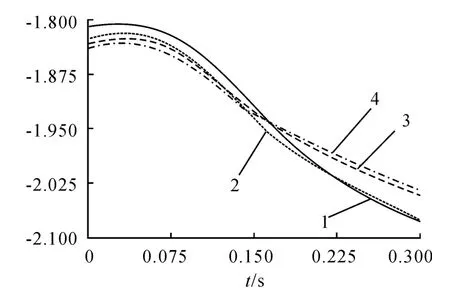
图3 炮口点Z向位移

图4 炮口点Y向角速度
从图3可以看出,不同的张紧力下,炮口点的Z向初始位置不一样,张紧力越大,炮口点与参考点的相对距离就越小。这是因为,张紧力越大,使得一、六负重轮悬挂进一步压缩,减小了地面对一、六负重轮的支撑力,为了能使火炮平衡,其它负重轮也一起压缩,车体质心降低,炮口点Z向初始位移变小。图中曲线1和2、曲线3和4的差距不大,可以判断当履带张紧力小于2.45e4 N时,履带不能张紧(射击时,履带张紧力的设计值为2.47e4 N)。当履带处于放松(曲线3、4)和张紧(曲线1、2)两种状态时,炮口点Z向位移的差距比较大,总的来说,在射击过程中,张紧状态的Z向位移大于放松状态的位移。
从图4可以看出,在射击过程中,张紧时炮口点Y向最大角速度基本一致,放松时的最大角速度也一致,而张紧时的最大角速度大于放松时的最大角速度,这是因为,当履带张紧时,一、六负重轮悬挂的刚性增大,履带系统的刚性也增大,火炮弹性元件吸收的能量较小,炮口的运动更为激烈。从图4中还可以看出,曲线先有一个向下的运动趋势,然后再开始迅速增大,但这个运动趋势产生的位移在图3中并不明显,这说明,射击过程中,炮口的运动并不像直观的那样,炮口直接向上抬起,而是在抬起前有一个向下运动的过程,正是这个运动会对弹丸膛内运动产生影响。
图5、图6为弹丸膛内运动时期炮口Z向速度和Y向角加速度。从图中可以看出,在这个时期,履带的张紧力对炮口的运动是有影响的,并进而影响了射击精度。如果履带没有完全张紧,在射击过程中,第六负重轮与主动轮之间的履带板会产生一个张紧过程,履带越放松,张紧时履带板间的作用力越大,反过来对车体运动的限制作用越大,炮口的运动越激烈。图5反应了这个相互作用情况,张紧力越小,炮口点Z向速度波动情况越大。图6中,炮口Y向角加速度随着张紧力的增大而减小,这是由于,弹丸出炮口前的作用时间极短,约为14 ms,悬挂系统还来不及响应,车体相当于在履带的拉力和地面的支撑力边界条件下的运动,履带的张紧力越大,车体相对越稳定,在膛内运动时期,炮身在绝对坐标系下的运动就越小,炮口的扰动情况越小。

图5 弹丸出炮口前炮口Z向速度

图6 弹丸出炮口前炮口Y向角加速度
5 结束语
对某自行火炮履带张紧力对炮口扰动问题进行了研究,结论为:张紧力的大小,影响了火炮的初始状态,张紧力越大,火炮的质心越低;火炮的运动可分为履带张紧和放松两种状态,在火炮发射过程中,当履带处于张紧状态时,炮口点最大Z向位移的峰值基本一致、最大Y向角速度的峰值基本一致,当处于放松状态时,最大Z向位移的峰值、最大Y向角速度的峰值也基本一致;张紧时的峰值大于放松时的值。
在弹丸膛内运动时期,履带张紧力对炮口运动的影响不能忽略。履带放松时,履带Z向速度波动比较大,会大大影响火炮的射击精度,因此,火炮在射击过程中,为了保证射击精度,履带应该张紧;弹丸膛内运动时期,炮口点Y向的角加速度随着张紧力的增大而减小,因此张紧力的增大有助于保证射击精度。需要指出的是,本文提的“放松”是指履带张紧力没有达到设计值,但履带仍处于完全撑开的状态。如果履带没有撑开,车体的角位移和线位移不再相互约束,履带在弹丸膛内运动时期不会影响炮口的初始扰动。
[1]曾晋春,杨国来,王晓锋.计及齿轮-齿弧接触的火炮动力学分析[J].弹道学报,2008,20(2):81-84.
[2]刘雷,陈运生,杨国来.基于接触模型的弹炮耦合问题研究[J].兵工学报,2006,27(6):984-987.
[3]葛建立,杨国来,陈运生,等.基于弹塑性接触/碰撞模型的弹炮耦合问题研究[J].弹道学报,2008,20(3):103-106.
[4]刘雷,陈运生.自行火炮发射过程的可视化仿真[J].火炮发射与控制学报,2005(4):10-14.
[5]康新中,马春茂,魏孝达.火炮系统建模理论[M].北京:国防工业出版社,2003.
[6]王钦钊,谷晓伟,李小龙,等.基于高机动条件下的坦克火控系统[J].兵工自动化,2012(3):19-21.
