基于BP神经网络与残差分析的船舶交通流量预测
2013-09-11翟久刚田延飞严新平
翟久刚,田延飞,严新平
(1.武汉理工大学a.能源与动力工程学院;b.航运学院,武汉 430063;2.交通运输部 中国海上搜救中心,北京 100736)
0 引言
船舶交通流量的准确预测有助于提高海事管理的效能,是船舶通航、航路规划与设计的重要参考依据.船舶交通流量实际上具有很大的随机性,月度船舶交通流量数据构成一个典型的非线性时间序列[1-2],采用线性回归、曲线方程等对其进行回归分析往往难以奏效.而人工神经网络具有极强的非线性映射能力,对非线性系统有良好的识别、预测能力,在信息预测领域已经得到广泛应用.以BP神经网络为例,由于其具有极强的非线性映射能力,对非线性时间序列具有很好的拟合能力,但过度拟合将导致其外推能力不佳,测试和预测精度变差,甚至出现与实际变化趋势相反的现象.为协调两者的矛盾,本文用神经网络对交通流量进行仿真及预测,从控制仿真残差入手设计和构建具有合适结构和预测精度等的网络,并应用于实际问题.
1 基本原理及流程设计
残差是指在回归分析中的实际观察值与回归估计值之差,以δ表示.显然,有多少对数据,就有多少个残差.针对交通流量这样的非线性系统,可通过建立合适的神经网络代替常规的回归方程,从而实现对该类特征系统的仿真及预测.神经网络对样本数据的仿真也会存在一定的偏差,因此将交通流量的观测值与按神经网络进行的仿真值之差定义为本文所指的残差.
残差分析[3-4]就是通过残差所提供的信息,分析出数据的可靠性、周期性或其他干扰.对残差的基本要求或残差分析的基本原理是:δ遵从正态分布N(0,σ2);δ与 σ 之比,称为标准化残差,以 δ*表示;δ*遵从标准正态分布N(0,1).实验点的标准化残差落在(-2,2)区间以外的概率≤0.05,若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点.
用神经网络替代回归方程的功能,结合残差分析,本文设计的基于BP神经网络与残差分析的船舶交通流量预测及分析流程见图1.
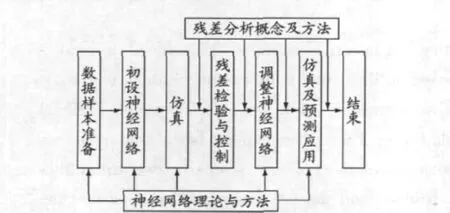
图1 基于BP神经网络与残差分析的交通流量预测流程
2 应用实例
2.1 初步仿真
采用上述流程对月度船舶交通流量进行仿真及预测.结合所做项目,调研得长江九江大桥观测线2008年8月—2011年7月之间月节点上船舶交通流量数据,见表1.
[5]和[6],本文用前3个月的交通流量数据预测第4个月的交通流量,如用2008年8—10月的交通流量数据,预测2008年11月的交通流量数据,即输入为[620504529],输出为[406].依次类推,从而表1的36个月度节点的原始交通流量数据构成33组原始样本.将前30组用作网络训练样本,后3组用作网络测试样本,则样本构成见表2.
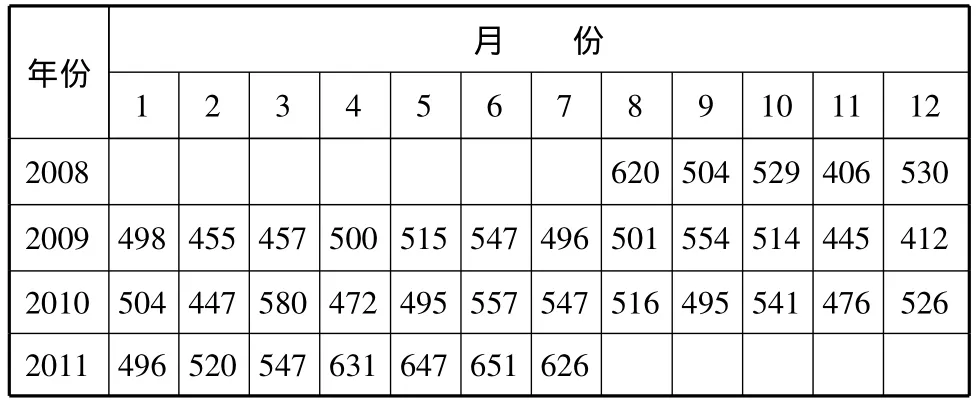
表1 长江九江大桥观测线月度船舶交通流量
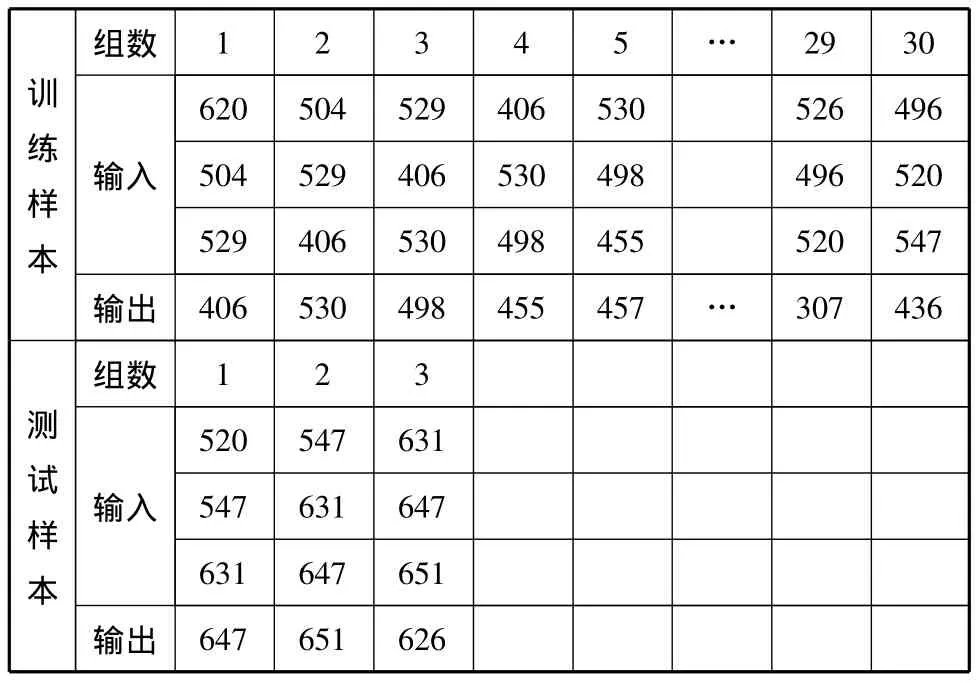
表2 原始数据样本分组列表
根据数据分组及输入输出的对应,设计网络结构为3-8-1的3层BP网络:其中输入层为3个神经元,输出层为1个神经元[7],中间隐含层神经元数为 8[8],见图 2.
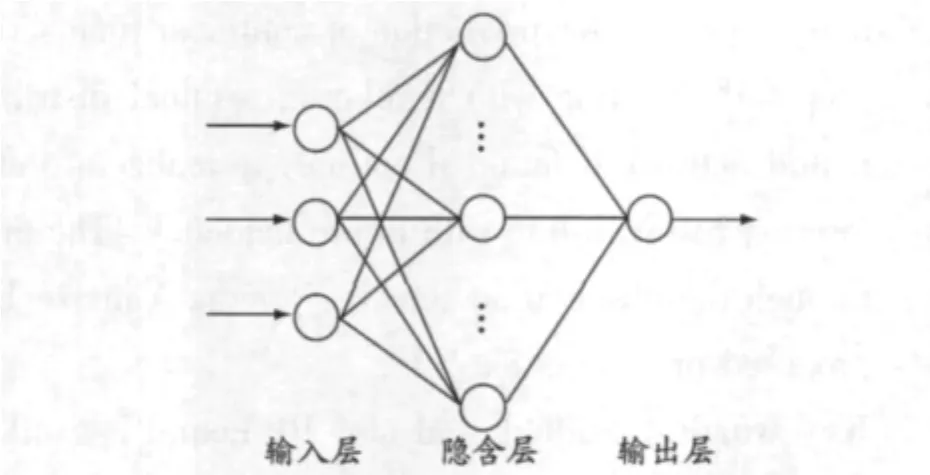
图2 设计的BP网络结构
神经网络的建立及仿真通过MATLAB软件实现.[9]主要设置为:隐层传递函数为“tansig”,输出层传递函数为“purelin”,训练函数为“trainlm”,训练目标为“0.1”学习速率,输入层权值阈值、网络层权值阈值均采取默认值(将训练目标分别设置为1e-2和1e-4,学习速率设置为0.01时分别进行训练,得到训练样本很高的拟合精度,但对测试样本仿真效果很差,甚至出现负值,故此处仅以最后一次的训练及仿真过程为例进行分析,其他情形的描述、图表等不再列出).在最后一次仿真过程中,采用33组样本时网络经过3步训练就达到设定的目标(0.1)要求.该网络经训练是否适合于对测试样本的仿真以及对未来交通流量的预测,可借助下面的残差分析判定.
2.2 残差分析
残差分析可利用MATLAB或SPSS软件实现.用MATLAB画出残差和标准残差分布相关性特征,见图3和4[10];用SPSS画出残差和标准残差的正态统计性特征,见图 5 和 6[11].
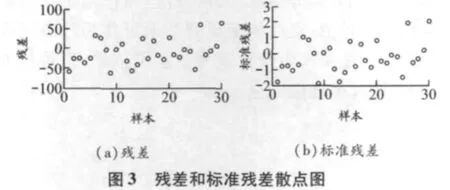
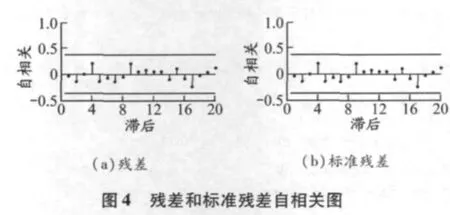
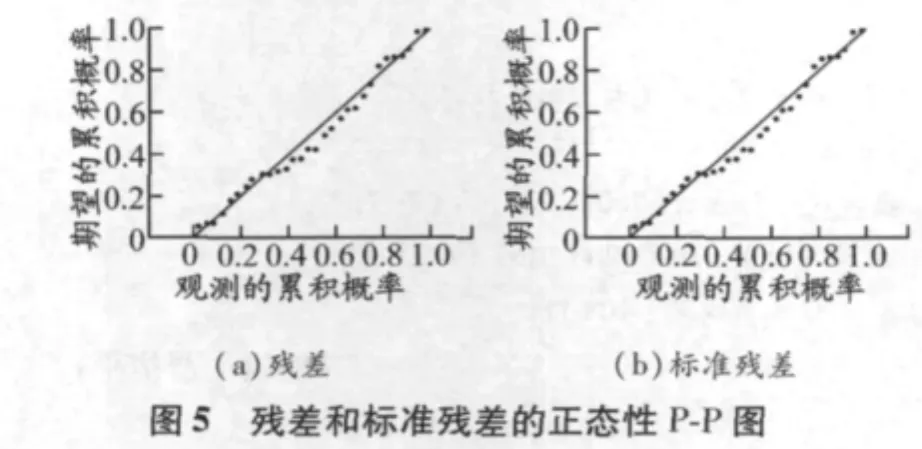
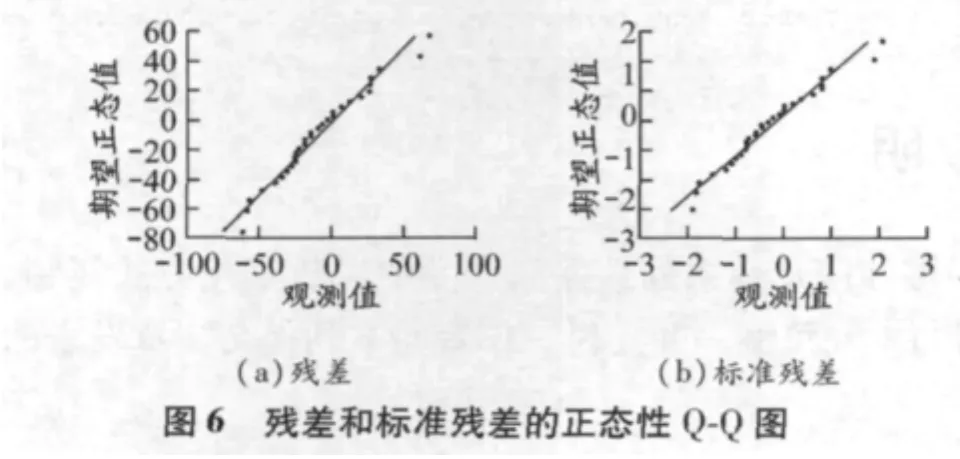
由图3可知:用神经网络对船舶交通流量仿真的残差和标准残差均落在0线附近的带状区域内,且无明显的趋势[3],初步说明该网络能够较好地拟合过去的流量数据;标准残差绝大多数落入[-1,1]区间,且几乎全部落入[-2,2]区间内,说明在95%置信度下该网络的拟合过程几乎没有异常点.由图4可知,残差和标准残差的自相关因数具有明显的截尾性,说明残差和标准残差时间序列已不存在相关性,可判定残差和标准残差为白噪声序列[12].根据图5和6,残差和标准残差具有相同的概率分布特征,且其概率分布与期望的正态分布检验直线基本吻合,故判断该网络拟合结果的残差和标准残差时间序列符合正态分布[13].
综上分析,采用前面建立的神经网络,得到交通流量仿真的残差和标准残差为正态白噪声时间序列,所建立的神经网络在95%的置信度水平下对历史数据的仿真较好,因此可以尝试利用该网络对交通流量进行仿真及预测.
2.3 预测结果分析
采用前述训练好的网络对所有样本进行仿真,画出相对误差((预测值-观测值)/观测值)曲线,并对未来12个月的交通流量进行预测.对长江九江大桥观测线2011年8月—2012年7月12个月节点上的船舶交通流量预测结果见表3(小数点后数字均省略,在整数位进1);仿真及预测结果见图7,其中第31~33节点处的值分别为测试样本的观测值和仿真值.

表3 长江九江大桥观测线船舶交通流量预测
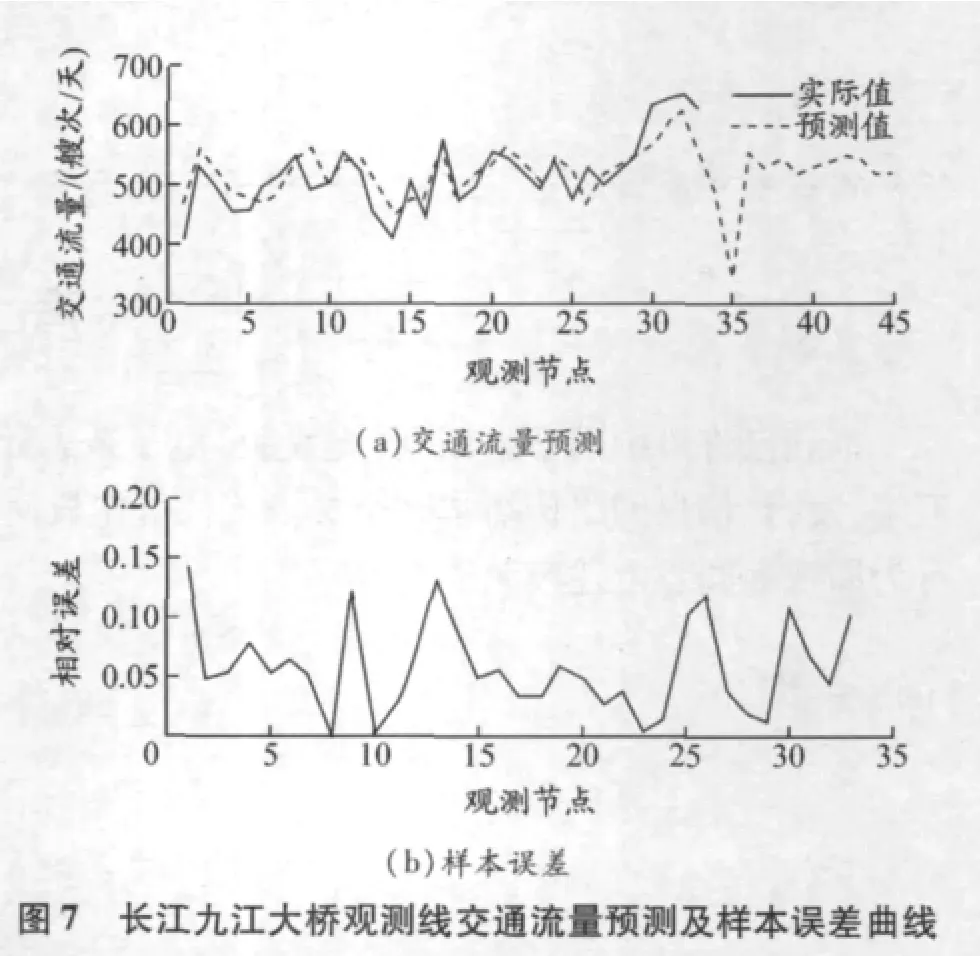
由图7可知,该网络能很好地拟合出前30组样本所反映的交通流量变化趋势,特别是对后3组测试样本,该网络也已仿真出交通流量“升高—滑落”的局部变化.另外,分析图7的相对误差曲线可知,所有样本仿真的相对误差在0.05左右波动,并没有出现较大的偏离或异常值.在预测部分,最先的两个预测值体现出交通流量的短时下降(在第35个节点处的值最小),其后的交通流量体现出较为平稳的波动变化,这与实际情况相符.由仿真及预测的效果可见,本文建立的网络能用于对交通流量的仿真及预测,网络输出值能够作为实际交通流量的参考.同时,其仿真和预测效果也与文中所述的残差分析和控制相呼应,即在控制残差的前提下设置神经网络的训练参数(如设置训练目标为0.1),以协调“过度拟合”与“预测误差”之间的矛盾.
3 结束语
从应用角度出发,以解决实际问题为目的,尝试将神经网络拟合与残差分析相结合,从控制残差为正态分布、残差通过白噪声检验[14]等方面协调神经网络的“拟合精度不够”与“因过度拟合导致预测误差偏大”之间的矛盾,以使所建立的BP神经网络能够较好地拟合过去时段的数据,又能对未来作出较合理、可信的预测.
将基于BP神经网络与残差分析的船舶交通流量预测应用于长江九江大桥观测线交通流量分析中,从预测效果分析可知,该方法可行,结论具有较高的参考价值.交通流量预测结果可作为海事管理部门合理配备海事管理资源的参考依据,以规范航行秩序、保障通航安全.
参考文献:
[1]曾慧,郑彩萍,王涛涛.基于(残差)Auto-Regressive模型利用MATLAB解决经济非平稳时间序列的预测分析[J].佳木斯大学学报:自然科学版,2008,26(1):71-74.
[2]王丽娜,肖冬荣.基于ARMA模型的经济非平稳时间序列的预测分析[J].武汉理工大学学报,2004,28(2):133-136.
[3]王敏.残差分析在统计中的应用[J].江苏统计,2000(8):24-25.
[4]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005.
[5]周少龙,周锋.基于时间序列的港口货物吞吐量GRNN预测模型[J].上海海事大学学报,2011,32(1):70-73.
[6]飞思科技产品研发中心.神经网络理论与MATLAB 7实现[M].北京:电子工业出版社,2005.
[7]朱武亭,刘以建.BP网络应用中的问题及其解决[J].上海海事大学学报,2005,26(2):64-66.
[8]严鸿,管燕萍.BP神经网络隐层单元数的确定方法及实例[J].控制工程,2009,16(S1):100-102.
[9]朱凯,王正林.精通MATLAB神经网络[M].北京:电子工业出版社,2010.
[10]张善文,雷英杰,冯有前.MATLAB在时间序列分析中的应用[M].西安:西安电子科技大学出版社,2007.
[11]杨小平,刘刚,赵晋.统计分析方法与SPSS应用[M].北京:清华大学出版社,2008.
[12]于宁莉,易东云,涂先勤.时间序列中自相关与偏相关函数分析[J].数学理论与应用,2007,27(1):54-57.
[13]宗序平,姚玉兰.利用Q-Q图与P-P图快速检验数据的统计分布[J].统计与决策,2010(20):151-152.
[14]施亮星,何桢.残差分析在计量型测量系统分析中的应用[J].工业工程,2008,11(3):108-111.
