基于量子理论的电子双缝衍射实验＊

李 宏，巴 诺，吴向尧，刘晓静，张斯淇，王 婧，马 季，董 赫

（吉林师范大学物理学院，吉林四平 136000）

基于量子理论的电子双缝衍射实验＊

李 宏，巴 诺，吴向尧，刘晓静，张斯淇，王 婧，马 季，董 赫

（吉林师范大学物理学院，吉林四平 136000）

用薛定谔方程求解电子在缝中的衍射波函数，用路径积分方法求解电子在缝外的衍射波函数，最终推导出衍射强度的关系式.理论计算结果和实验测得数据符合相当好，验证了量子理论方法能够精确解释电子的衍射现象.

薛定谔方程；双缝衍射；路径积分

从19世纪中期至今，物质波在物理学得到了突飞猛进的发展，波动性的假说由德布罗意提出，已经有很多实验验证了这个假设［1］.由于粒子具有波粒二象性，所以人们用经典模型研究物质波的衍射和干涉不是严格精确的.精确求解粒子的衍射和干涉，必须用量子理论［2－7］.笔者采用量子理论方法研究电子双缝衍射，通过对薛定谔方程的求解得到电子在缝中的衍射波函数，电子在缝外的衍射波函数可由路径积分方法严格求解，最终推导出衍射强度的关系式.理论计算的结果和测得的实验数据符合相当好，从而用量子理论更好地解释了电子衍射这一物理现象.由于实验的衍射图样会受到退相干机制影响，所以用退相干机制对干涉强度进行修正，从而得到更好的理论结果［8－9］.

1 求解缝中电子波函数φ（r，t）

取a为缝宽，b为缝长，c为缝厚，d为两缝之间距离，缝长方向为x轴，缝宽方向为y轴，缝厚方向为z轴，如图1所示.

在t时刻有一质量为M的电子沿z轴正方向入射，其波函数表示为

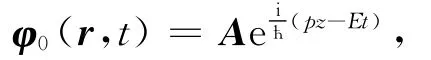
其中A为常矢量.含时薛定谔方程为

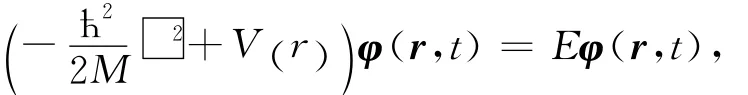
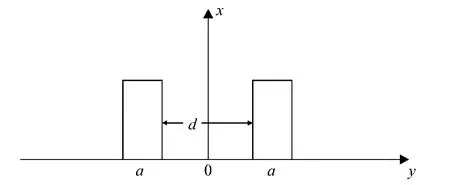
图1 电子双缝结构示意

其中：E为电子的能量；M为电子的质量.

左缝中的势能为

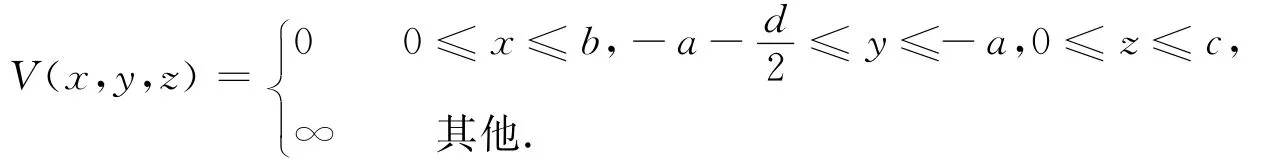
其中c是缝的厚度.在缝中V＝0.则不含时薛定谔方程可写为

求解（1）式并通过分离变量法求解缝内波函数可得

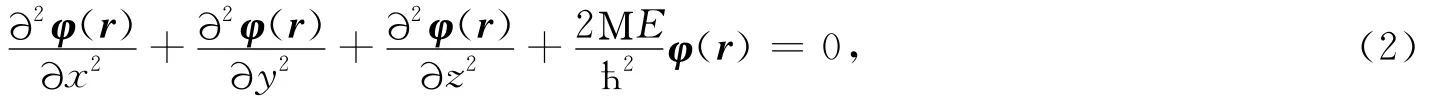
其满足的边界条件为

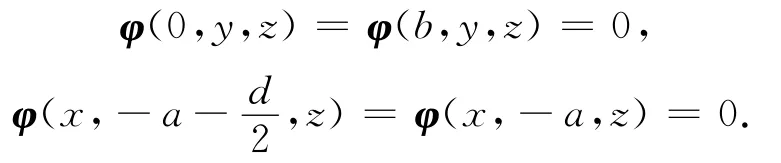
通过分离变量φ（x，y，z）＝X（x）Y（y）Z（z）可得（2）式的一般解为

则含时薛定谔方程的一般解为

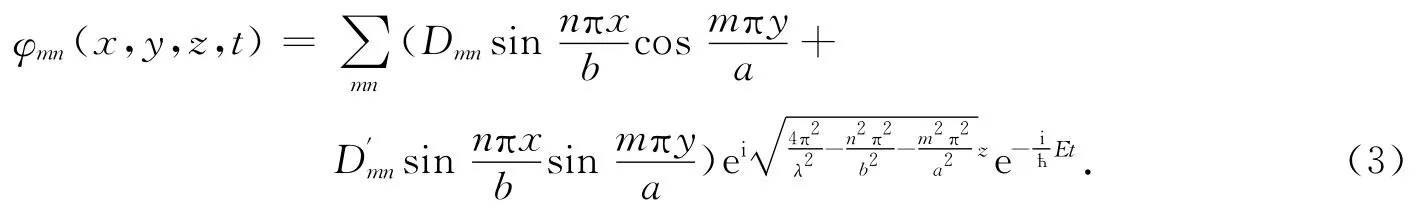
由波函数在z＝0处连续可得

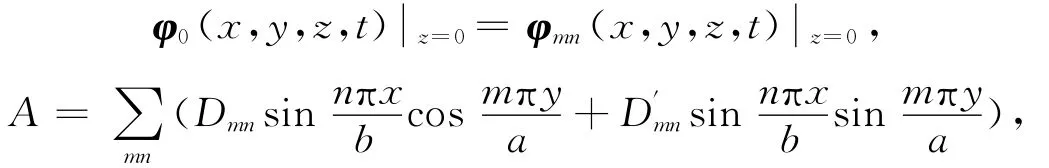
通过二重傅立叶级数展开求得

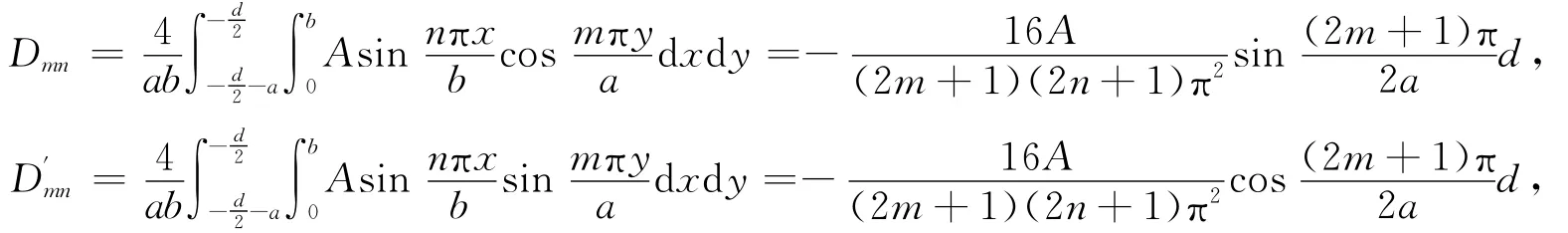
其中m，n＝0，2，3，....

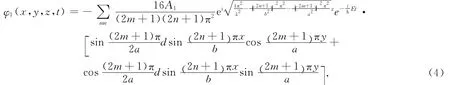
同理，可求得右缝中的波函数为

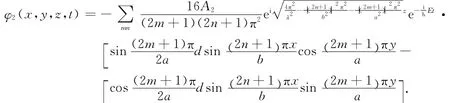
2 求解电子在缝后衍射波函数ψr，（t）

电子衍射示意图如图2所示.

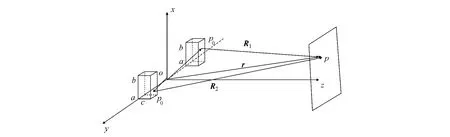
图2 电子在缝外衍射示意

设任意一点p0点在缝面上，任意一点p点衍射屏上，粒子到达z＝c平面p0点的时间为t0，由（4）式得

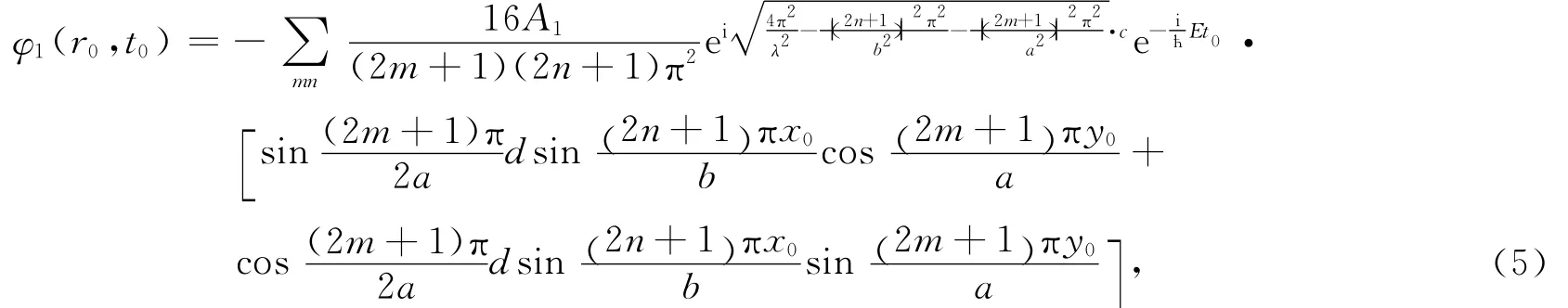
观察屏上t时刻的波函数由路径积分公式得

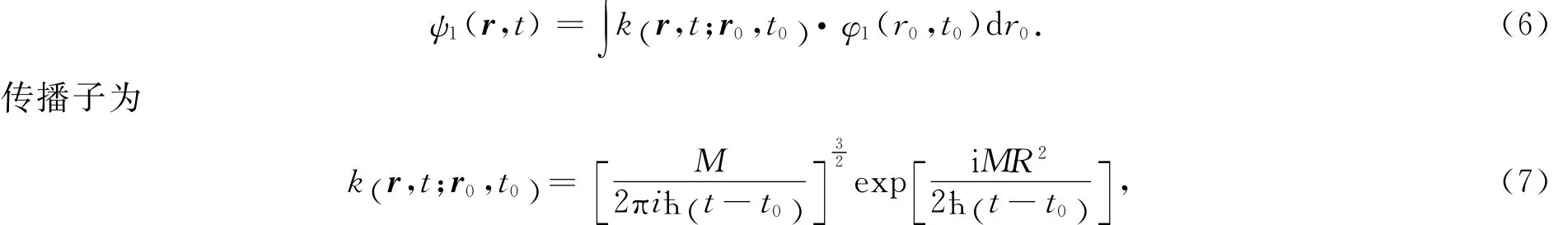
其中：M为粒子质量；R为p0点到p点之间的距离；（t－t0）为粒子从p0点飞行到p点的时间.将（7）式代入（6）式可得

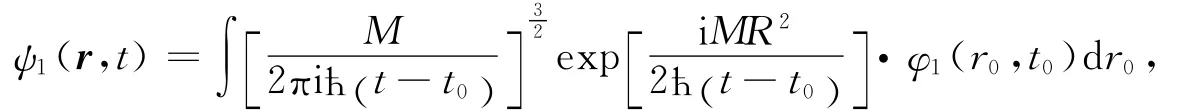
其中dr0＝dx0dy0.由图2可知

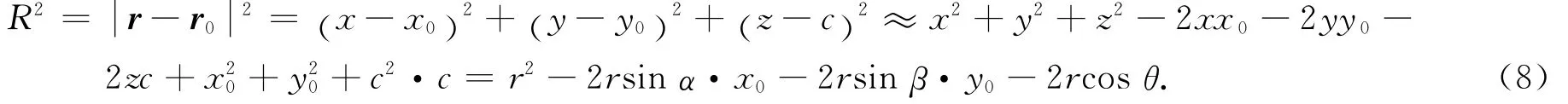
（8）式中的x20，y20和c2为二阶无穷小量，可忽略，则

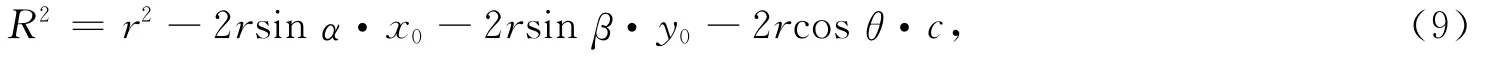
其中：α为r与yz平面的夹角；β为r与xz平面的夹角；θ为r与z轴的夹角.

将（9）式代入（8）式化简得到左缝缝外衍射波函数为

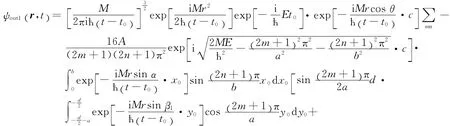
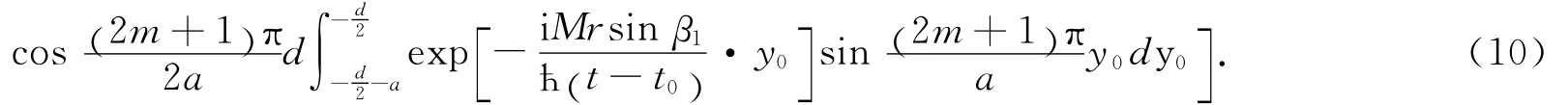
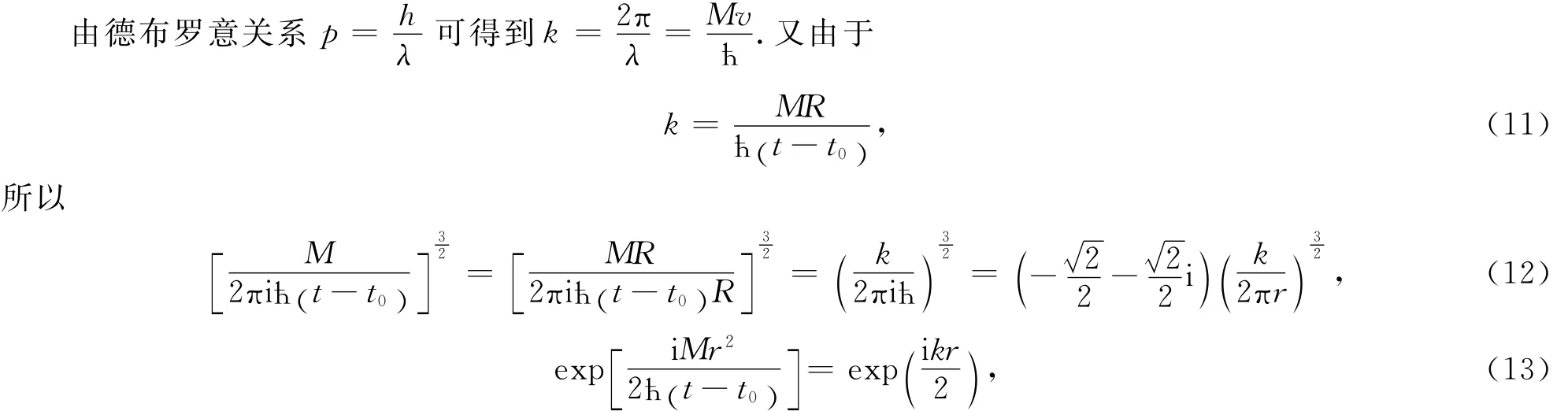
把（11）至（13）式代入（10）式得到衍射屏上的波函数为

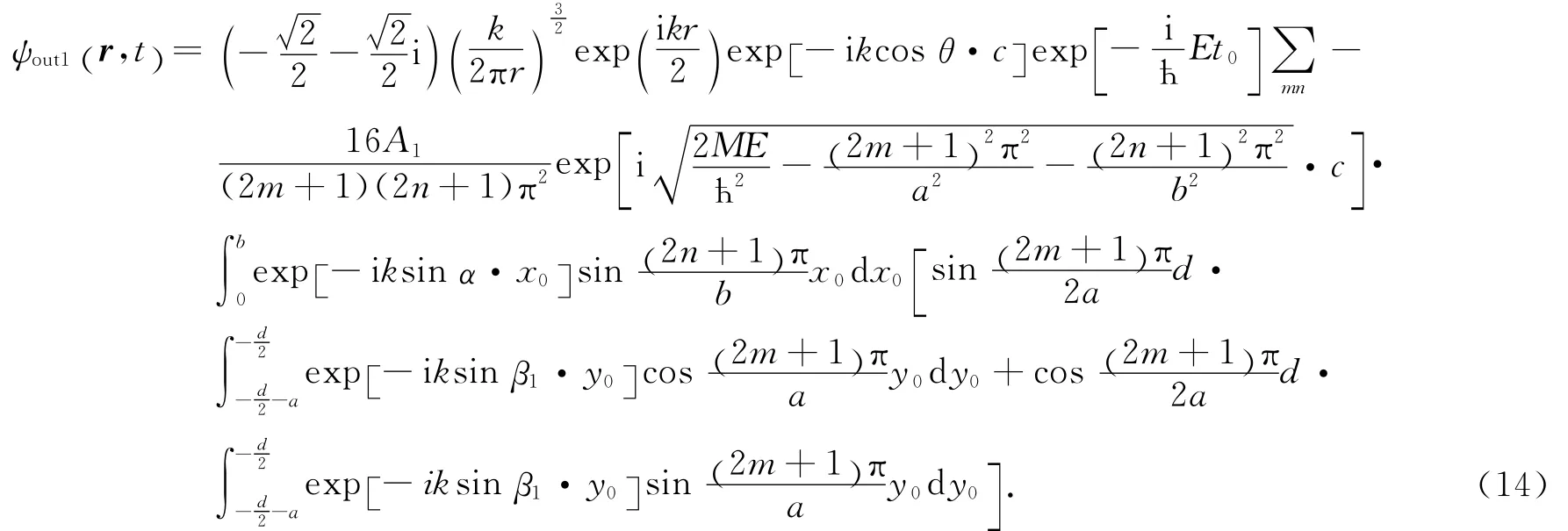
同理，右缝在衍射屏上的波函数为

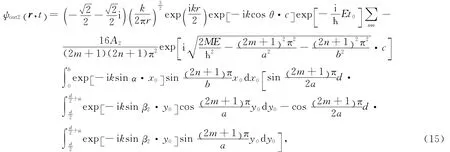
其中cos2θ＋sin2α＋sin2β＝1.

双缝衍射总的波函数为

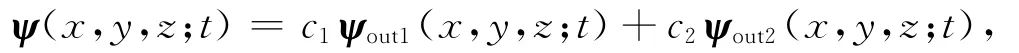
3 修正屏幕上相对干涉强度

由文献［8］可知干涉波函数为

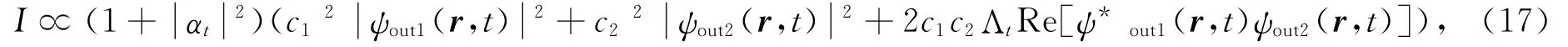
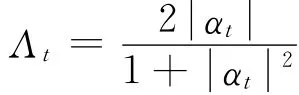
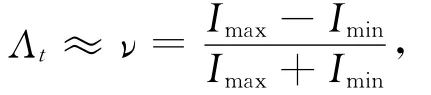
其中Imax为中间衍射强度的最大值，Imin为与中间最大值相邻的第1个最小值为.由实验数据计算得到的两缝衍射波函数ψout1（r，t）和ψout2（r，t）可以通过量子力学方法严格求解得到.

4 数值分析

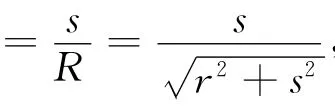
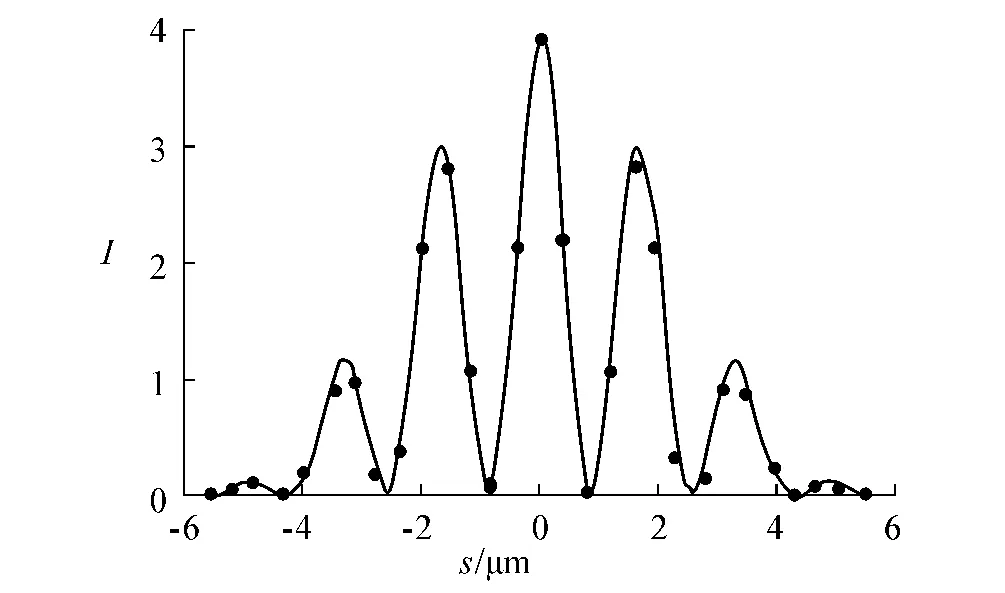
图3 电子双缝衍射理论结果与实验数据比较

5 结论

文中采用量子理论方法研究了电子的双缝衍射，得到了电子衍射强度解析式，理论计算的结果与实验测得数据符合相当好，从而证明了可以用量子理论方法精确描述电子的干涉、衍射现象.

［1］ STREKALOV D V，SERGIENKO A V，KLYSHKO D N，et al.Observation of Two－Photo“Ghost”Interference and Diffraction［J］.Physics Review Letters，1995，74（18）：3 600－3 603.

［2］ SANZ A S，BORONDO F，BASTIAANS M J.Loss of Coherence in Double Slit Diffraction Experiments［J］.Physics Review，2005，A71（4）：042 103－042 109.

［3］ AMDT M，NAIRZ O，VOSS－ANDREAE J，et al.Wave－Particle Duality of C60Molecules［J］.Nature，1999，401，680－688.

［4］ ANGELO M D，MARIA V，CHEKHOVA M V，et al.Two－Photon Diffraction and Quantum Lithography［J］.Physics Review，2001，87（1）：013 602－013 607.

［5］ MICHEL G，ALEXANDRE G.Numerical Simulation of the Double Slit Interference with Ultracold Atoms［J］.American Journal of Physics，2005，73：507－515.

［6］ NAIRZ O，ARNDT M，ZEILINGER A.Quantum Interference Experiment with Large Molecules［J］.Am.J.Phys.，2003，71：319－325.

［7］ WU X Y，ZHANG B J，HUA Z，et al.Quantum Theory Approach for Neutron Single and Double－Slit Diffraction［J］.International Journal of Theoretical Physics，2010，49：2 191－2 199.

［8］ SANZ A S，BORONDO F，BASTIAANS M J.Loss of Coherence in Double－Slit Diffraction Experiments［J］.Phys.Rev.A，2005，71：042103－11.

［9］ ANTON Z，ROLAND G，SHULL C G，et al.Single and Bouble－Slit Different of Neutrons［J］.Modern Physics，1988，60：1 067－1 073.

［10］ WANG Li，ZHANG Bai－jun，HUA Zhong，et al.Quantum Theory of Electronic Muliple－Slit Diffraction［J］.Theoretical Physics，2009，121（4）：685－693.

（责任编辑 陈炳权）

Quantum Theory of Electronic Double－Slit Diffraction

LI Hong，BA Nuo，WU Xiang－yao，LIU Xiao－jing，ZHANG Si－qi，WANGJing，MA Ji，DONG He
（Institute of Physics，Jilin Normal University，Siping 136000，Jilin China）

The electronic wave function in the slits is obtained by the Schrodinger equation，and electron diffraction wave function outside the slits by the strict solutions of path integral method.The diffraction intensity is proportional to the square of diffraction wave function.Then，the formula of electronic double－slit diffraction intensity can be obtained.It is found that the theoretical calculation result of quantum theory and the experimental measurement data tally pretty well.So，the method of quantum theory can explain electron diffraction phenomenon precisely.

Schrodinger equation；double－slit diffraction；path integral

O413.1

A

10.3969／j.issn.1007－2985.2013.03.006

1007－2985（2013）03－0025－06

2013－03－10

国家自然科学基金资助项目（11247201）；吉林师范大学研究生创新科研计划资助项目

李 宏（1989－），男，吉林公主岭人，吉林师范大学物理学院硕士研究生，主要从事量子理论物理学研究.

吴向尧（1965－），男，安徽安庆人，吉林师范大学物理学院博士，教授，主要从事凝聚态理论物理研究.E－mail：wuxy2066＠163.com.