Positive Solution for Nonlinear Higher－Order Neutral Variable Delay Difference Equations with Continuous Arguments＊

YANG Jia－shan，LIU Xing－yuan

（Department of Science and Information，Shaoyang University，Shaoyang 422004，Hunan China）

Positive Solution for Nonlinear Higher－Order Neutral Variable Delay Difference Equations with Continuous Arguments＊

YANG Jia－shan，LIU Xing－yuan

（Department of Science and Information，Shaoyang University，Shaoyang 422004，Hunan China）

Positive solution for a class of nonlinear higher－order neutral variable delay difference equations with continuous arguments is studied.Using the fixed point theorem in Banach space and a lot of inequality techniques，some sufficient conditions for the existence of eventually positive solution for the equations are obtained.The examples are presented to illustrate the effects of our theorems.

eventually positive solution；continuous arguments；nonlinear；neutral delay difference equation；fixed point theorem

1 Introduction

Obviously，eq.（1）includes a lot of neutral delay difference equations，which have a very wide range of applications in scientific research and practice.So any research results about oscillation and asymptotic are very important.Our purpose in this article is to obtain new criteria for the nonoscillation of eq.（1）.With the fixed point theorem in Banach space and a lot of inequality techniques，some new sufficient conditions for the existence of eventually positive solutions of the equations are obtained.In this article，our attention is restricted to those solutions x（t）for eq.（1）where x（t）is not eventually identically zero.As is customary，we recall that a solution x（t）for eq.（1）is said to be an eventually positive solution if x（t）＞0for sufficiently large t（t≥t0）.

We consider the following assumptions：

2 Main Results

ProofFrom condition（H2），choose n1≥n0sufficiently large such that－

Clearly，Tis continuous.For every x∈B1and n≥n1，we have

Now we show that Tis a contraction mapping on B1.In fact，for∀x（1），x（2）∈B1and n≥n1，we have

Furthermore，we can obtain，for sufficiently large n，

hence，x（t）is a bounded eventually positive solution for eq.（1）.This completes the proof.

Theorem2 Assume that conditions（H1）and（H2）hold，if there exists a constant psuch that－1＜p≤b（t）＜0.Then，the eq.（1）has a bounded eventually positive solution.

ProofSimilar to the proof of theorem 1.Choose n2≥n0sufficiently large such that

Define a subset B2in Bas

and then it is easy to see that B2is a bounded，closed and convex subset of B.We define an operator T：B2→Bas the following

Clearly，Tis continuous.For∀x∈B2and n≥n2，we have

and

By similar argument，for∀x（1），x（2）∈B2and n≥n2，we have

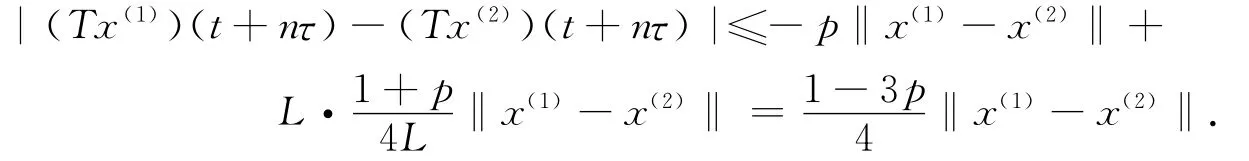
It follows that

Furthermore，we can obtain，for sufficiently large n，

hence，x（t）is a bounded eventually positive solution of eq.（1）.The proof of the theorem is completed.

Theorem3 Assume that conditions（H1）and（H2）hold，if there exist constants p1and p2such that－∞＜p1≤b（t）≤p2＜－1.Then，the eq.（1）has a bounded eventually positive solution.

ProofSimilar to the proof of theorem 1.Choose n3≥n0sufficiently large such that

bounded，closed and convex subset of B.We define an operator T：B3→Bas following：

Obviously ，Tis continuous.For∀x∈B3and n≥n3，wehave

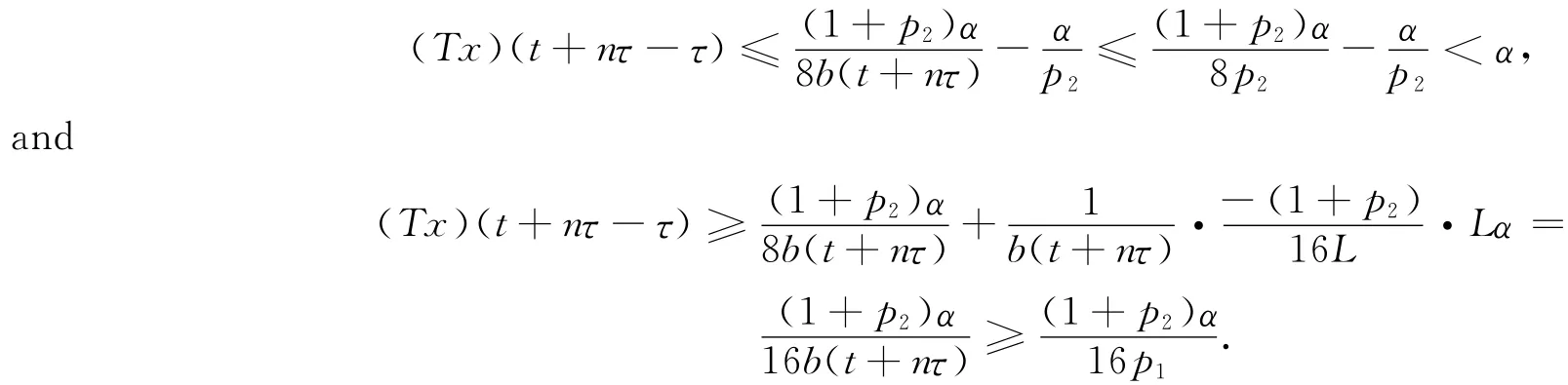
Furthermore，we can obtain，for sufficiently large n，

hence，x（t）is a bounded eventually positive solution for eq.（1）.This completes the proof.

Example1 Consider the following second－order neutral difference equation with continuous arguments：

（2）If take

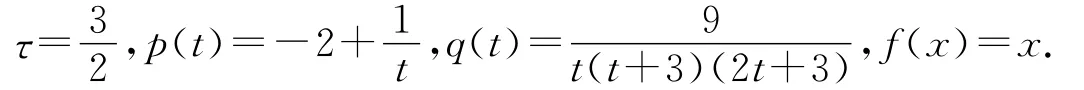
Then，one can see that the conditions of theorem 3are satisfied.So，by theorem 3，this equation exists a bounded eventually positive solution.In fact，it is easy to verify that x（t）＝1is such a solution.

［1］ WANG Dong－hua，ZHONG Xiao－zhu，LIANG Jing－cui，et al.Existence of Positive Solutions for a Class of Higher－Order Neutral Delay Difference Equations［J］.Journal of Wuhan University of Technology，2006，28（12）：145－147.

［2］ YANG Jia－shan，SUN Wen－bing.Bounded Oscillation for Second－Order Nonlinear Difference Equation with Variable Delay［J］.Chinese Quarterly Journal of Mathematics，2011，26（4）：516－520.

［3］ YANG Jia－shan，LI Ji－meng.Oscillation Theorems of Second Order Nonlinear Difference Equations with Maxima［J］.Journal of Anhui University：Natural Science Edition，2012，36（3）：19－22.

［4］ YANG Jia－Shan，LIU Xing－yuan.Oscillation of a Class of Second Order Nonlinear Neutral Difference Equations［J］.Journal of Kunming University of Science and Technology：Natural Science Edition，2012，37（5）：88－94.

［5］ HUANG Mei，SHEN Jian－hua.On the Second Order Neutral Difference Equations with Continuous Arguments［J］.Journal of Natural Science of Hunan Normal University，2005，28（3）：4－6.

［6］ WANG Pei－guang，WU Meng.Oscillation Criteria of Second Order Damped Difference Equation with Continuous Variable［J］.Applied Mathematics Journal of Chinese Universities（Ser.A），2006，21（1）：44－48.

［7］ HUANG Mei，SHEN Jian－hua.A Class of Even Order Neutral Difference Equations with Continuous Arguments［J］.Journal of Southwest University：Natural Science Edition，2007，29（10）：29－34.

［8］ YANG Jia－shan.Oscillation and Nonoscillation Criteria for a Class of the Second Order Nonlinear Difference Equations with Continuous Arguments［J］.Journal of Systems Science and Mathematical Sciences，2010，30（12）：1 651－1 660.

［9］ YANG Jia－shan，FANG Bin.Oscillation and Nonoscillation Criteria for Higher Order Difference Equations with Continuous Arguments［J］.Journal of Anhui University：Natural Science Edition，2011，35（3）：14－18.

［10］ YANG Jia－shan，LI Ji－meng.Oscillation and Nonoscillation Criteria for the Higher Order Nonlinear Difference Equation with Continuous Variable［J］.Journal of Hefei University of Technology：Natural Science，2010，33（6）：934－938.

［11］ YANG Jia－shan，WANG Yu.Existence of Positive Solutions and Oscillation for a Class of Higher Order Nonlinear Delay Difference Equations with Continuous Arguments［J］.Journal of Shaoyang University：Natural Science Edition，2012，9（1）：4－8.

［12］ YANG Jia－shan，LI Ji－meng.The Oscillation of a Class of Higher Order Nonlinear Variable Delay Difference Equations with Continuous Arguments［J］.Journal of Minzu University of China：Natural Sciences Edition，2011，20（1）：31－36.

［13］ LI Guo－qin，ZHONG Xiao－zhu，LIU Na，et al.Oscillation of the Second Order Neutral Delay Difference Equations with Continuous Arguments［J］.Mathematics in Practice and Theory，2012，42（17）：258－262.

［14］ ZHONG Wen－yong.Nonlinear Boundary Value Problem for Second Order Dynamic Equations on Time Scales［J］.Journal of Jishou University：Natural Sciences Edition，2012，33（4）：6－10.

［15］ YANG Jia－shan.Forced Oscillation of Second－Order Nonlinear Dynamic Equation with Variable Delay on Time Scales［J］.Journal of Shanxi University：Natural Sciences Edition，2011，34（4）：543－547.

（责任编辑 向阳洁）

具连续变量的高阶非线性变时滞差分方程的正解

杨甲山，刘兴元
（邵阳学院理学与信息科学系，湖南邵阳 422004）

研究了一类具有连续变量的高阶非线性变时滞中立型差分方程，利用Banach空间的不动点原理和一些分析技巧，得到了这类方程存在最终正解的几个新的充分条件，同时给出实例验证其有效性.

最终正解；连续变量；非线性；中立型时滞差分方程；不动点原理

O175.7

A

O175.7

A

10.3969／j.issn.1007－2985.2013.03.001

1007－2985（2013）03－0001－06

＊Received date：2012－12－15

Supported by Natural Science Foundation of Hunan Province（12JJ6006）；Hunan Province Science and Technology Project（2012FJ3107）

Biography：Yang Jia－shan（1963－），male，was born in Chengbu County，Hunan Province，professor of Shaoyang University；research area are differential and difference equation.