基于分段间隙函数的螺旋锥齿轮时变啮合参数分析

刘志峰，郭春华，杨文通，蔡力钢，张志民

(北京工业大学 机械工程与应用电子技术学院，北京 100124)

由于啮合阻尼、啮合刚度的动态变化和制造误差、安装误差、摩擦等原因而产生的间隙的存在，使得螺旋锥齿轮系统是一个具有参数激励的强非线性系统。目前国内外学者针对该动力学特性的研究已经作了大量的工作，建立了多种数学分析模型。Wang等［1-2］以一对准双曲面齿轮为研究对象建立了数学模型，将啮合参数按基频谐波展开，采用数值法求解，讨论了时变参数、系统参数及间隙非线性对齿轮副动力学特性的影响。Kahraman等［3-5］建立了直齿轮副的单自由度间隙非线性模型，将啮合刚度、间隙非线性函数、传动误差和外部激励展成多项谐波形式，用谐波平衡法求解。Litak等［6］考虑了轴的挠性，建立了三自由度齿轮模型，指出在二自由度模型上增加一个额外自由度，齿轮副将显示不同的动态特性。

李润方等［7］考虑了正弦型时变啮合阻尼，并假设与啮合刚度成正比，且相应于轮齿分离的速度也为非线性函数，指出非线性时变阻尼可采用常数阻尼来代替。唐进元等［8］对一类阻尼和刚度系数均含时变参数的强非线性齿轮系统进行了研究，针对时变阻尼项和刚度项之间的耦合作用使周期解的平均值发生漂移问题提出了一种改进的能量迭代法，并推导出系统主振动的幅频和相频响应方程。陈思雨等［9］考虑了时变刚度和摩擦时轮齿间隙及载荷参数对齿轮系统冲击动力学响应的影响，并首次研究了非线性动力学的脱啮冲击。王建平等［10-11］建立了考虑动态啮合刚度、传递误差和齿侧间隙等多种非线性因素的直齿圆柱齿轮系统非线性动力学模型，将时变刚度按5次谐波展开，齿侧间隙按3次多项式拟合，并用多尺度法分析了齿轮系统组合共振和谐振。张锁怀等［12］考虑了不平衡质量、主动轴转速波动和齿轮副齿侧间隙，并建立了单级齿轮传动系统的拍击振动模型，推导出了相邻两次碰撞之间的映射关系式。申永军等［13-14］建立了考虑间隙、时变刚度和静态传递误差的直齿轮副动力学模型，研究了阻尼比和激励水平对幅频曲线的影响。刘国华等［15］提出了考虑轮齿弹性振动和单双齿啮合区变化的齿轮机构多体弹性非线性动力学模型。

上述研究主要利用解析、数值和实验的方法，分析齿轮时变刚度、齿侧间隙、静态传递误差对齿轮系统的参数激励、谐波共振、冲击等动力学响应，并未涉及由于间隙函数的分段变化，而产生的时变啮合参数在不同的啮合状态对螺旋锥齿轮啮合特性的影响。因此，本文根据啮合点法向位移与间隙不同关系下间隙函数的变化，考虑啮合阻尼和啮合刚度的时变性，研究平均啮合阻尼、谐波啮合阻尼、谐波啮合刚度在不同啮合状态下对螺旋锥齿轮副传动过程中啮合特性的影响规律。

1 数学分析模型

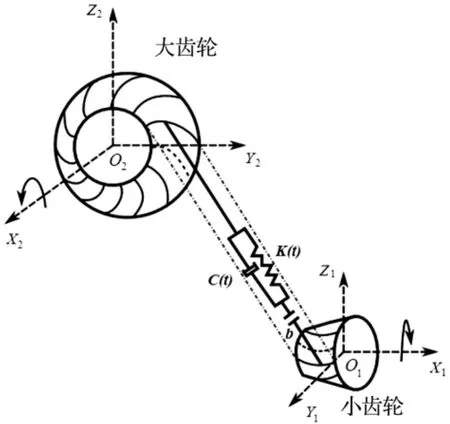
图1 螺旋锥齿轮副啮合模型Fig.1 Meshing model of spiral bevel gear

根据螺旋锥齿轮的传动特点，建立了一对齿轮副传动模型，如图1所示。假定传动轴和支撑部件均为刚性体，则主、从动齿轮的扭转平衡方程分别为:

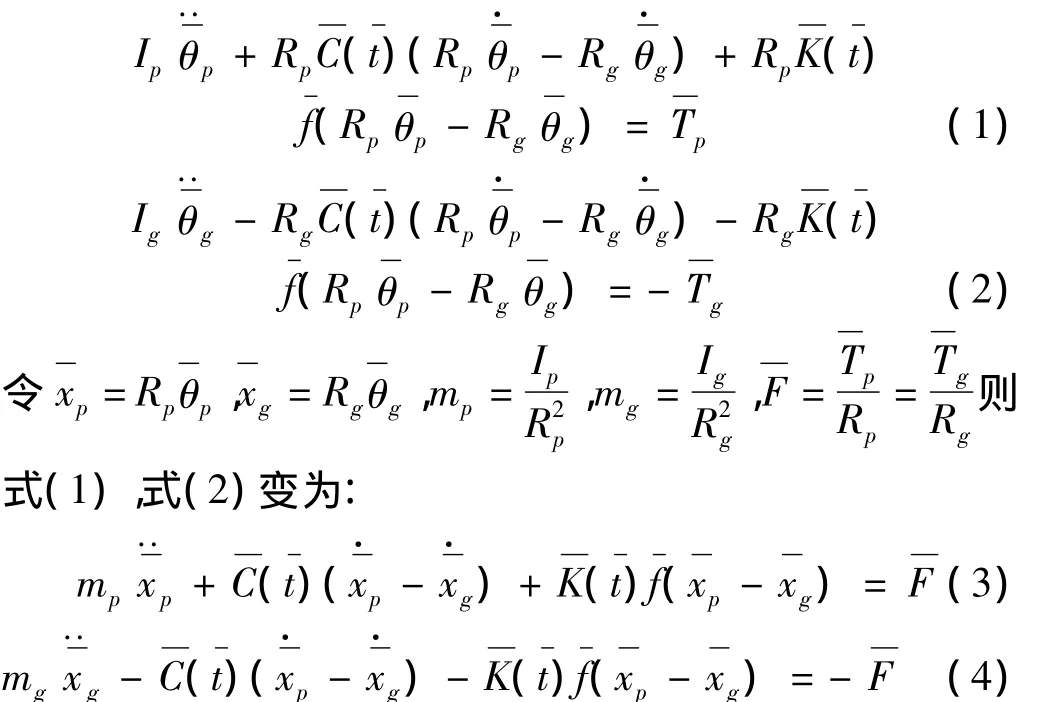
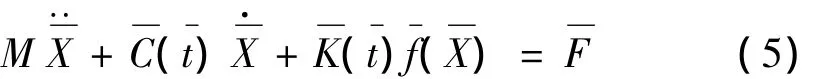
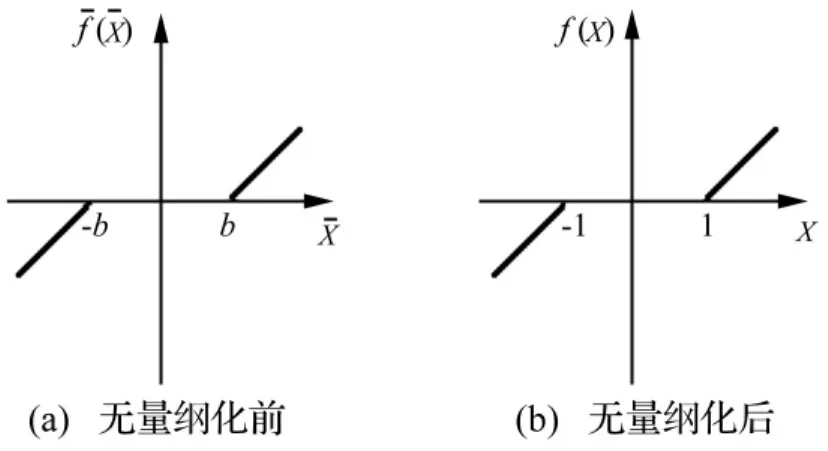
图2 间隙函数Fig.2 Clearance function

2 时变啮合参数、间隙函数的无量纲化

螺旋锥齿轮啮合过程中，会出现单齿对啮合及多齿对啮合交替变化的情况，使得啮合刚度始终处在不断的变化中。相对于单齿啮合区，齿轮的啮合综合刚度较小，啮合弹性变形较大;在双齿对啮合区，由于是两对轮齿同时承受载荷，因此齿轮的啮合综合刚度较大，啮合弹性变形较小。随着齿轮副的连续运转，轮齿的弹性变形呈周期性变化，引起齿轮副角速度周期性变化，进而导致齿轮副振动。此外在考虑摩擦时，应将常数啮合阻尼描述为非线性时变啮合阻尼，即阻尼项也含时变参数。将阻尼和刚度按傅里叶级数展开，并取前两项，可得:令

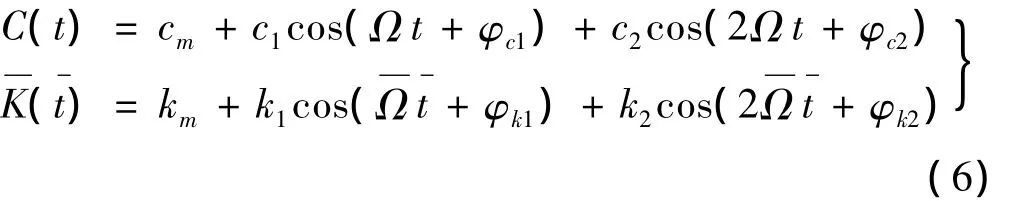
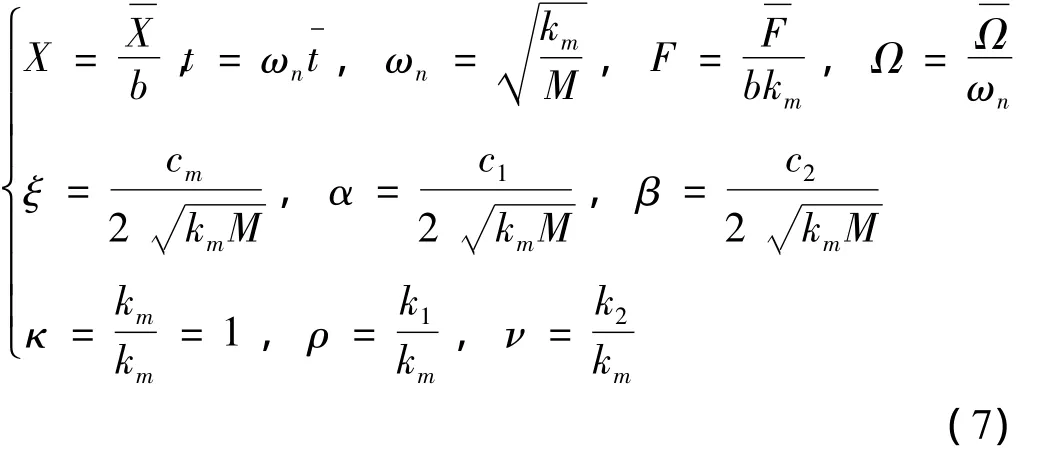
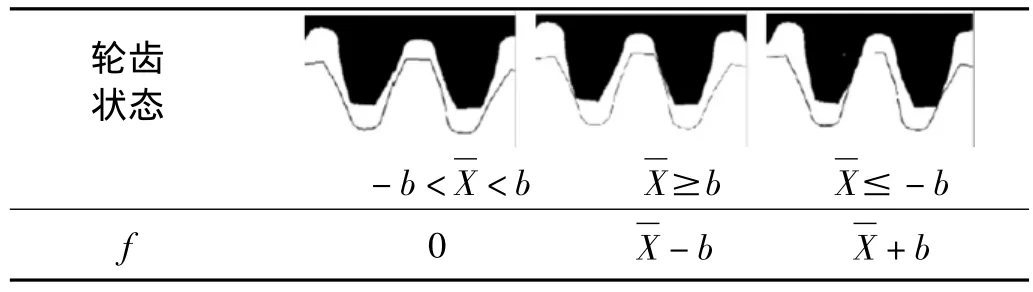
表1 轮齿不同啮合状态下间隙函数变化Tab.1 Variation of clearance function under different meshing state

在轮齿啮合过程中，由于啮合点法向位移与齿侧间隙关系的变化，使得间隙函数也随之变化。将间隙函数处理成图2(a)所示的对称形式，并对其无量纲化，如图2(b)所示。轮齿不同啮合状态下的间隙函数如表1所示。无量纲化前后的表达式为:

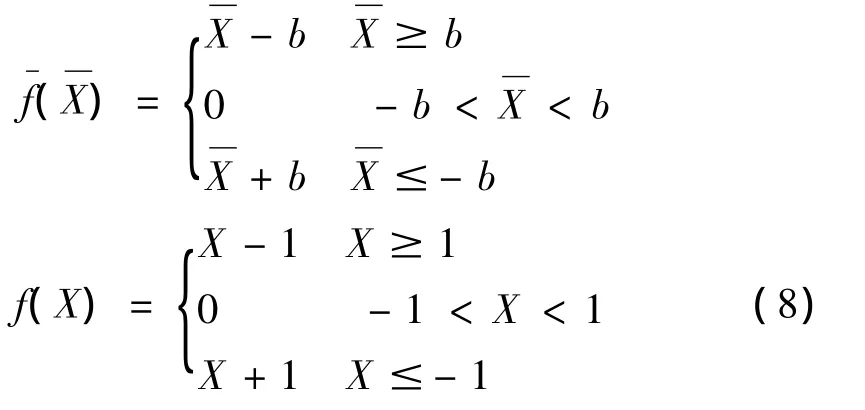
根据文献［1，8］可知

将式(6)～式(8)代入式(5)得

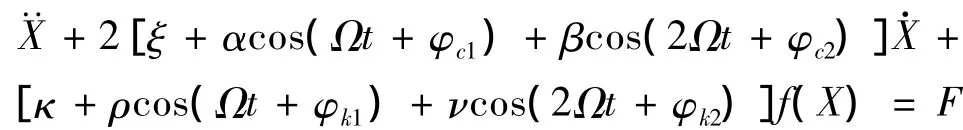
各物理量意义见表2。

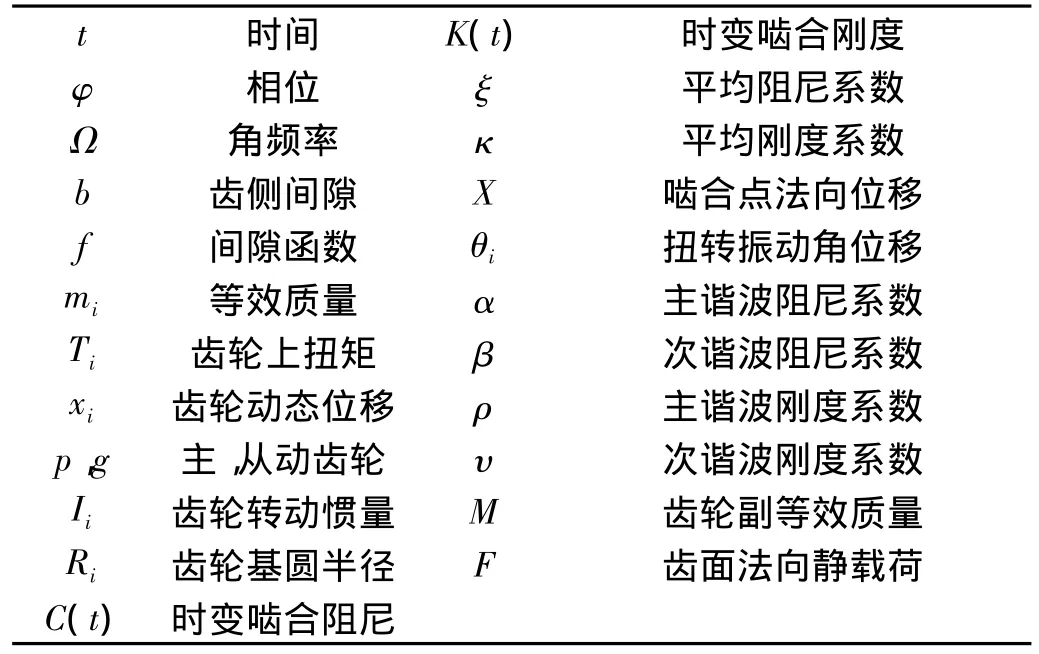
表2 物理量对照表Tab.2 Table of physical symbol

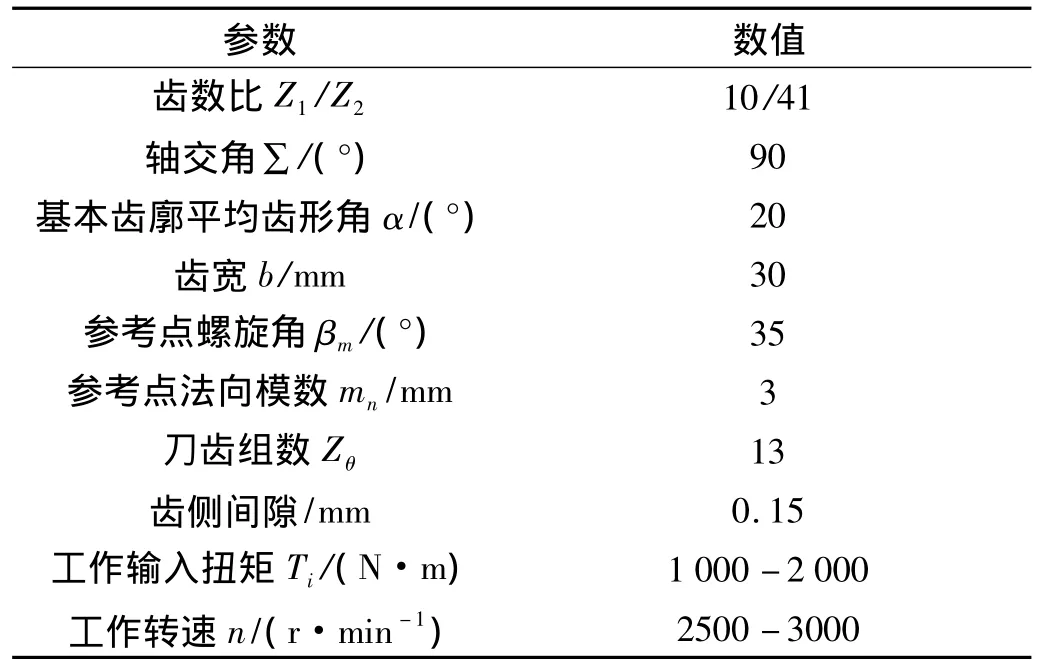
表3 螺旋锥齿轮传动系统参数Tab.3 Transmission system parameters of spiral bevel gear

3 齿轮系统振动因素分析

令 φc1=φc2=φk1=φk2=0，取F=0.8，下面分别从-1＜X＜1，X≤-1，X≥1三种情况讨论动态激励项的影响，螺旋锥齿轮传动系统相关参数见表3。

3.1 －1＜X＜1情况

当-1＜X＜1时，齿轮副扭转方程表示为

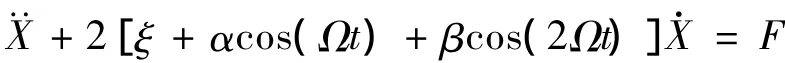
图3所示为齿轮系统振动的位移-时间曲线。由图可知:随平均阻尼系数ξ的增大，系统趋向收敛。以t=150为例，当ξ=0.03时，啮合点法向位移为1 765，ξ=0.15时，啮合点法向位移为389。平均阻尼系数的增大，使啮合点法向位移振动幅值有了明显的衰减，齿轮啮合过程中的振动迅速降低，提高了传动平稳性。

图4所示阻尼含有主谐波激励时，啮合点法向位移均方根值变化情况。以平均阻尼系数ξ=0.15为例，当主谐波阻尼系数α=0时，啮合点法向位移均方根值为148，为一条水平的光滑直线;α=0.01时，法向位移均方根最小值为173.34，最大值为294.61;当 α =0.10 时，位移均方根最小值为282.11，最大值为400.76。由于加入了主谐波激励项，啮合点法向位移在整个频率范围内已不再是一条光滑的恒值曲线，而是在多个频率处出现波动，且随频率的增加，其值呈现上升趋势，并且主谐波系数的增加，会使位移均方根值迅速增大。

图5为阻尼含有次谐波项时，啮合点法向位移均方根值变化曲线。以 ξ=0.15，α=0.10为例，当 β=0.03时，均方根值最小为278，最大值为403.15。β=0.05时均方根值最小为285.76，最大值为447.51。可见当-1＜X＜1时，次谐波阻尼系数的变化，也可影响齿轮副的啮合特性。

3.2 X≤－1情况

当X≤-1时，齿轮副系统的扭转方程表示为:

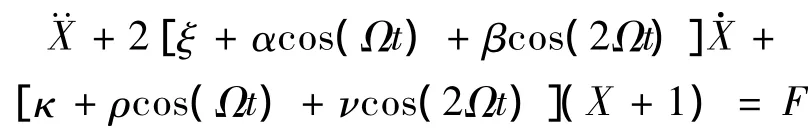
图6为X≤-1时，只考虑平均阻尼系数ξ情况下，齿轮副振动特性变化曲线。ξ=0.03时，在Ω=1和Ω=2处均出现了峰值，其值为3.95;ξ=0.05时，仅在Ω=1处出现了峰值，其值为2.64;ξ=0.15时，峰值降为1.18。随着ξ的增加，出现峰值的频率点由原来的两个减少到一个，且峰值随之减小。这表明平均阻尼系数的增加有利于降低振动峰值，减小轮齿变形。

图7所示为X≤-1时，主谐波阻尼系数α对齿轮副系统振动影响曲线。以ξ=0.1为例，随着α的变化，啮合点法向位移均方根值变化很小，在整个频率范围内最大误差为0.97%。图8所示为X≤-1时，次谐波阻尼系数β的变化对位移均方根值影响曲线。以ξ=0.1，α =0.05为例，在 Ω =1 频率处，β=0时啮合点法向位移均方根值为1.54，β =0.02 时其值为 1.47，最大误差为4.5%。当X≤-1时，主谐波阻尼系数和次谐波阻尼系数的变化对啮合点法向位移均方根值几乎没有影响。因此，分析齿轮副振动时将啮合阻尼系数视为常数是合理的。

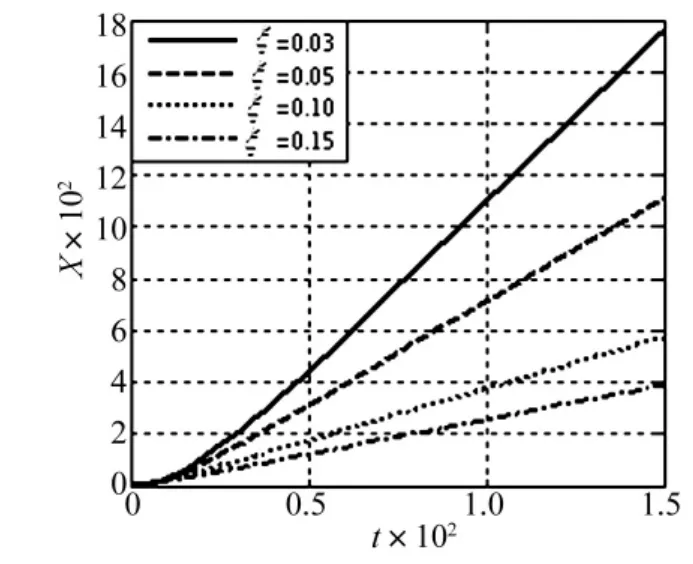
图3 -1＜X＜1，ξ影响振动位移曲线(κ =1，ρ =0.2，ν =0.04)Fig.3-1＜X ＜1，vibration displacement curves on ξ

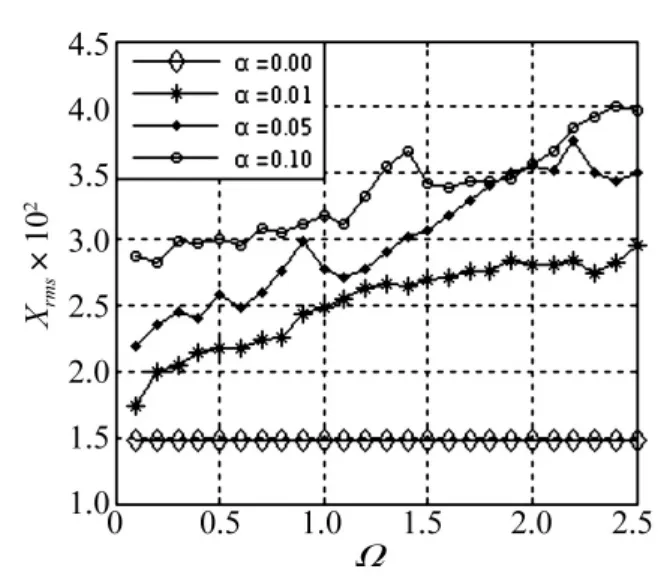
图4 -1＜X＜1，α影响振动位移曲线(κ =1，ρ=0.2，ν=0.04)Fig.4-1＜X ＜1，vibration displacement curves on α

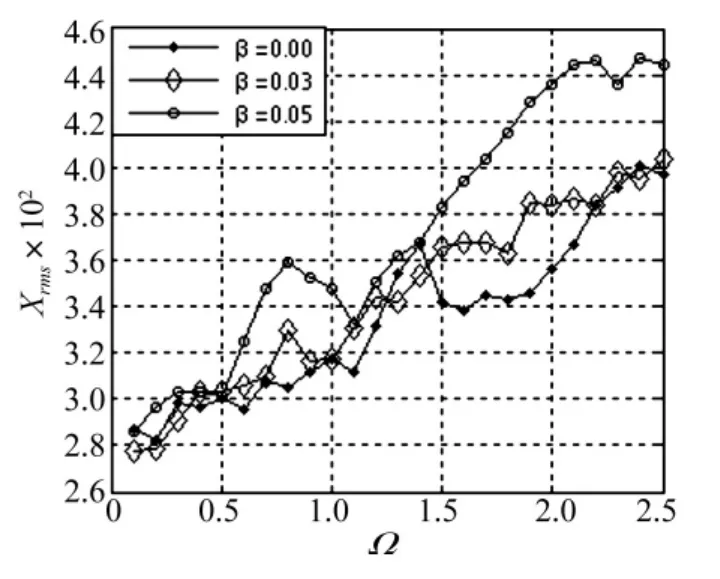
图5 -1＜X＜1，β影响振动位移曲线(κ =1，ρ=0.2，ν =0.04)Fig.5 -1 ＜X ＜1，vibration displacement curves on β

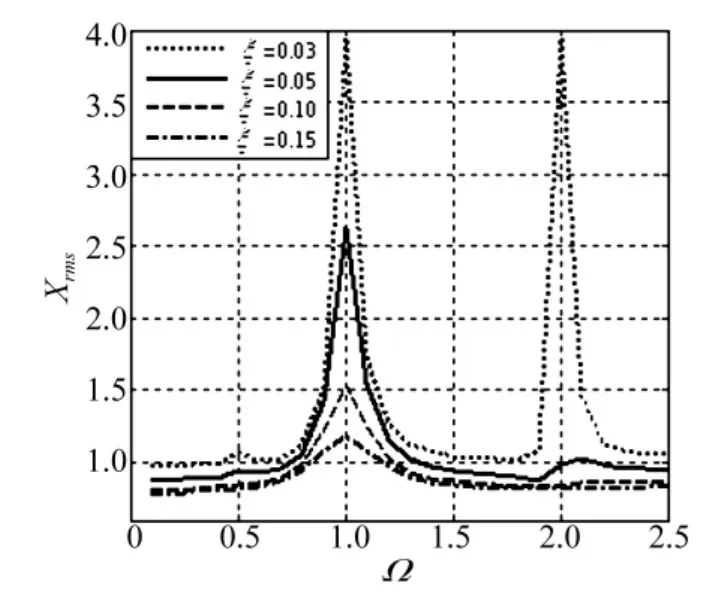
图6 X≤-1，ξ影响振动位移曲线(κ =1，ρ =0.2，ν =0.04)Fig.6 X≤ -1，vibration displacement curves on ξ

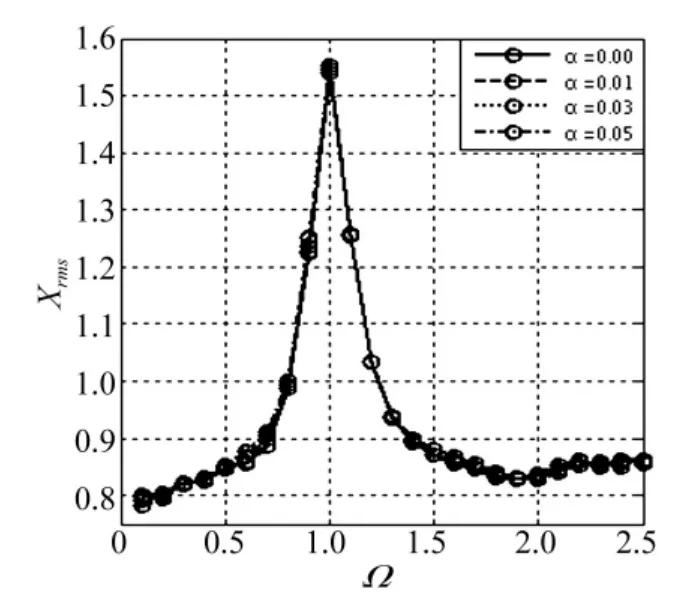
图7 X≤-1，α影响振动位移曲线(κ =1，ρ=0.2，ν=0.04)Fig.7 X≤ -1，vibration displacement curves on α

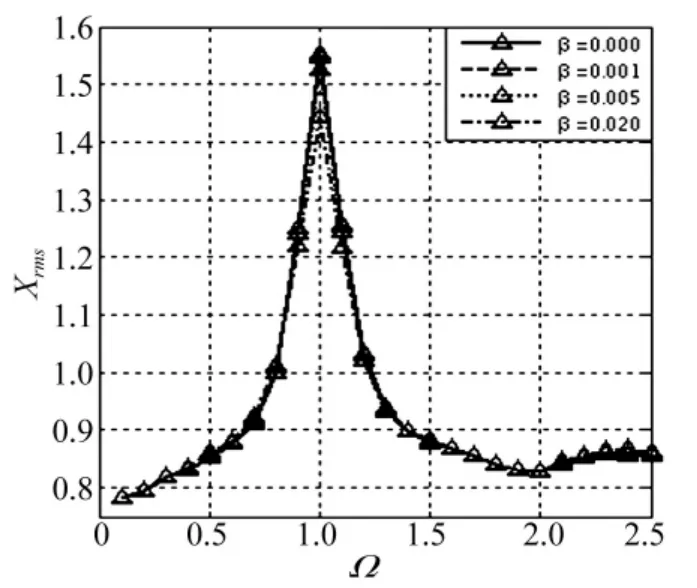
图8 X≤-1，β影响振动位移曲线(κ =1，ρ=0.2，ν =0.04)Fig.8 X≤ -1，vibration displacement curves on β

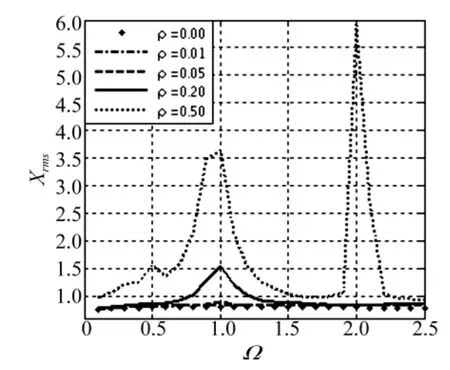
图9 X≤-1，ρ影响振动位移曲线(ξ =0.1，α =0.05，β =0.001)Fig.9 X≤ -1，vibration displacement curves on ρ

图10 X≤-1，ν影响振动位移曲线(ξ =0.1，α =0.05，β =0.001)Fig.10 X≤ -1，vibration displacement curves on ν

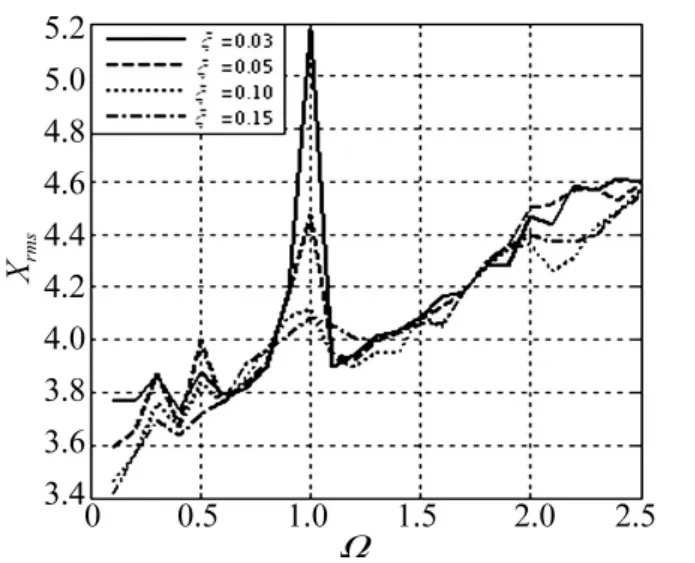
图11 X≥1，ξ影响振动位移曲线(κ =1，ρ=0.2，ν =0.04)Fig.11 X≥1，vibration displacement curves on ξ

主谐波刚度系数ρ对齿轮副动态特性影响如图9。在平均刚度系数相同的情况下，ρ从0增加到0.05时，仍以线性特性为主;ρ继续增加到0.2，在Ω=1处首次出现峰值1.54;当ρ=0.5时，在Ω=1附近和Ω=2处均出现了峰值，Ω=1附近的两个峰值分别为3.47和3.64，Ω=2处的峰值为5.92。随着次谐波啮合刚度系数ν的增加，Ω=1处的峰值变化不是很明显，而Ω=2处的峰值逐渐增大。图10所示，当ν由0增加到0.20时，Ω=2处的峰值也由5.92增加到8.60。因此表明引入主谐波和次谐波刚度项时，均会对齿轮副振动特性产生影响。

3.3 X≥1情况

当X≥1时，齿轮副系统的扭转方程可以表示为

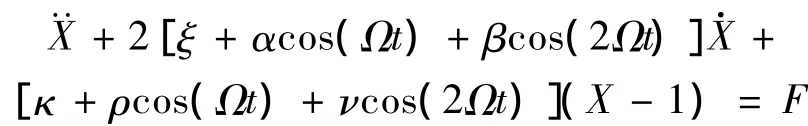
由图11可看出:ξ=0.03时，Ω=1处出现峰值，其值为5.18;ξ=0.05时，Ω =1还是为峰值频率，但值降为4.47;随着 ξ分别增加到 0.10 和 0.15，不再存在峰值，Ω=1处位移均方根值分别为4.12和4.09。

图12所示为当X≥1时，主谐波阻尼系数α对齿轮副系统振动影响曲线。以ξ=0.15为例，由图可看出在Ω=1.5频率处，α=0时的啮合点法向位移均方根值为4.26，α=0.10时的啮合点法向位移均方根值为4.06，最大误差为4.7%。当增加次谐波阻尼项时，如图13所示，以 ξ=0.15，α =0.1 为例，β =0.01 时的啮合点法向位移均方根值为4.55，β=0.03时的啮合点法向位移均方根值为4.81，最大误差为5.4%。由此可看出当X≥1时，阻尼含时变激励项对啮合点法向位移均方根值影响不明显。因此在这个阶段，非线性时变阻尼也可由常数阻尼来代替。

图14所示为主谐波刚度系数ρ对齿轮副啮合特性位移影响曲线。不考虑谐波啮合刚度项，即ρ=ν=0时，Ω=2为啮合点法向位移均方根峰值频率，峰值为3.5。当仅将ρ分别增加到0.01和0.2时，位移均方根值在整个频率内均随频率Ω的增大而增大，峰值消失。但当ρ增加到0.5时，在Ω=1附近和Ω=2处均出现了峰值，其值分别为 5.47、5.31 和5.07。

图15所示，当含有次谐波刚度项时，以κ=1，ρ=0.5为例，随次谐波刚度系数ν的增加，在Ω=1附近和Ω=2处的峰值均发生了变化。ν=0时，三个峰值分别为5.47、5.31 和 5.07;ν=0.05 时，三个峰值分别为 5.29、5.17 和5.18;ν =0.10 时，三个峰值分别为 5.15、5.09和5.44。即随着次谐波刚度系数的增加，Ω=1附近的两个峰值在减小，而Ω=2处的峰值却随着次谐波刚度系数的增加而增大。

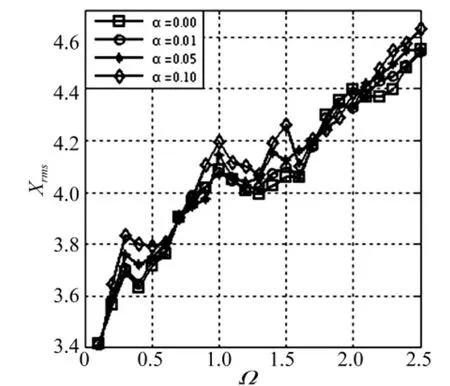
图12 X≥1，α影响振动位移曲线(κ =1，ρ=0.2，ν =0.04)Fig.12 X≥1，vibration displacement curves on α

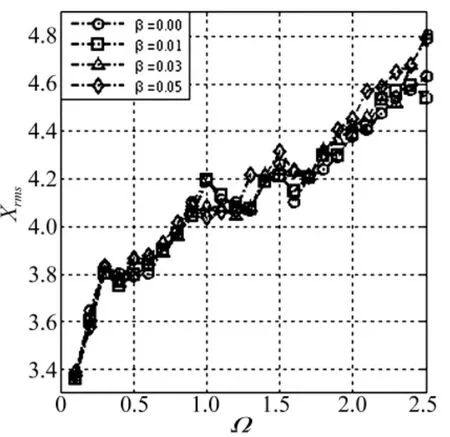
图13 X≥1，β影响振动位移曲线(κ =1，ρ=0.2，ν=0.04)Fig.13 X≥1，vibration displacement curves on β

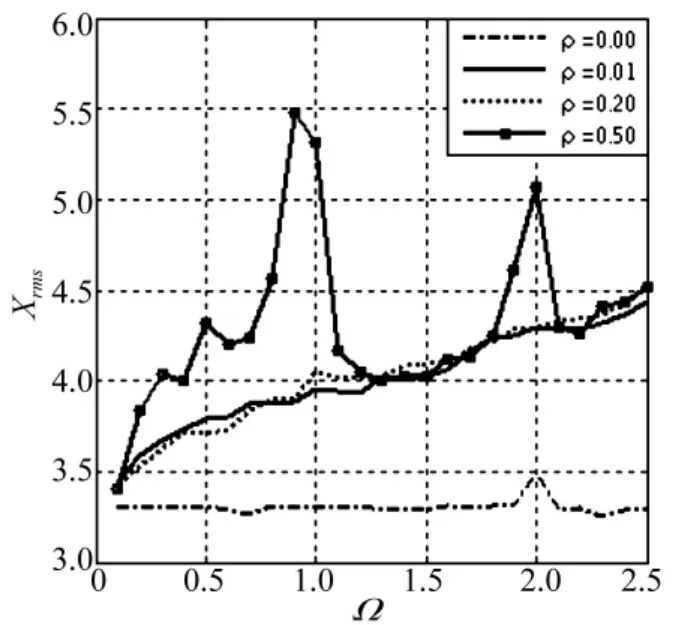
图14 X≥1，ρ影响振动位移曲线(ξ =0.1，α =0.05，β =0.001)Fig.14 X≥1，vibration displacement curves on ρ

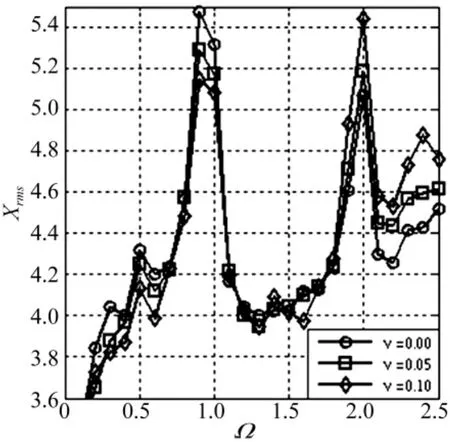
图15 X≥1，ν影响振动位移曲线(ξ=0.1，α =0.05，β =0.001)Fig.15 X≥1，vibration displacement curves on ν

4 结论

本文基于间隙函数的分段特性，考虑啮合阻尼和啮合刚度的时变性，并采用二次谐波展开的形式，讨论了平均啮合阻尼、谐波啮合阻尼和谐波啮合刚度在不同啮合状态下对螺旋锥齿轮副传动过程中动力学特性的影响。确定了时变啮合参数下的螺旋锥齿轮副，在其不同啮合阶段时的啮合特性，为螺旋锥齿轮的减振和降噪提供了理论依据。

(1)-1＜X＜1时，平均啮合阻尼系数的增大使振动迅速衰减，实现减振降噪;引入谐波阻尼项和谐波阻尼系数的增大均不利于齿轮传动的平稳啮合，啮合点法向位移均方根曲线原有的光滑恒值特性将被打破，取而代之的是多个频率点处出现波动，且增大谐波阻尼系数会使位移均方根值变大。

(2)X≤-1时，平均啮合阻尼系数的增大抑制了齿轮啮合过程中的振动峰值，使齿轮传动趋于平稳;谐波阻尼影响很小，在这个啮合状态分析齿轮副振动时将啮合阻尼系数视为常数是合理的。谐波刚度项系数的增大会使齿轮副啮合过程出现振动峰值，与此同时，谐波刚度项系数越大，亦会使某些频率点处峰值越大，不利于齿轮副的平稳传动。

(3)X≥1时，增大平均阻尼和降低主谐波刚度减弱了系统的非线性;谐波阻尼的增加对系统的振动特性影响较小，可采用常数阻尼代替非线性时变阻尼。次谐波刚度系数的增大会产生不确定的情况，会使一些频率处的振动峰值降低，一些频率处振动峰值升高。

［1］Wang J，Lim T C，Li M F.Dynamics of a hypoid gear pair considering the effects of time-varying meshing parameters and backlash nonlinearity［J］.Journal of Sound and Vibration，2007，308:302-329.

［2］ Wang J， Lim T C. Effectoftooth meshingstiffness asymmetric nonlinearity for drive and coast sides on hypoid gear dynamics［J］.Journal of Sound and Vibration，2009，319:885-903.

［3］Ma Q L， Kahraman A.Subharmonic resonances of a mechanical oscillator with periodically time-varying，piecewise-nonlinear stiffness［J］.Journal of Sound and Vibration，2006，294:624-636.

［4］Kahraman A，Blankenship G W.Experiments on nonlinear dynamic behaviorofan oscillator with clearance and periodically time-varying parameters［J］.ASME Journal of Applied Mechanics，1997，64:217-226.

［5］Al-shyyab A，Kahraman A.Non-linear dynamic analysis of a multi-meshing gear train using multi-term harmonic balance method:period-one motions［J］.Journal of Sound and Vibration，2005，284:151-172.

［6］Litak G，Friswell M I.Vibration in gear systems［J］.Chaos，Solitons and Fractals，2003，16:795-800.

［7］李润方，王建军.齿轮系统动力学-振动、冲击和噪声［M］.北京:科学出版社，1997.

LI Run-fang， WANG Jian-jun. Gear system dynamicsvibration，shock and noise(in chinese)［M］.Beijing:Science Press，1997.

［8］唐进元，陈思雨.阻尼和刚度项含时变参数的强非线性振动系统周期解研究［J］.振动与冲击，2007，26(10):96-100.

TANG Jin-yuan，CHEN Si-yu.Study on periodic solutions of strong nonlinear systems with time-varying damping and stiffness coefficient［J］.Journal of Vibration and Shock，2007，26(10):96-100.

［9］陈思雨，唐进元，谢耀东.齿轮传动系统的非线性冲击动力学行为分析［J］.振动与冲击，2009，28(4):65–69.

CHEN Si-yu，TANG Jin-yuan，XIE Yao-dong.Analysis of nonlinear impact dynamic behavior for a gear pair system with time-varying stiffness and friction［J］.Journal of Vibration and Shock，2009，28(4):65–69.

［10］王建平，王玉新.运用多尺度法对齿轮系统组合共振特性的分析［J］.西安理工大学学报，2005，21(1):1-5.

WANG Jian-ping，WANG Yu-xin.Combination resonance of spur gear system analyzed using multi-scale approach［J］.Journal of Xi’an University of Technology，2005，21(1):1-5.

［11］王建平，王玉新.考虑动态刚度、传递误差及齿侧间隙的齿轮系统谐振分析［J］.机械设计，2005，22(9):26-28.

WANG Jian-ping，WANG Yu-xin.Resonance analysis of gear system with the consideration of dynamic rigidity，transmission error and tooth backlash［J］.Journal of Machine Design，2005，22(9):26-28.

［12］张锁怀，沈允文，董海军，等.单级齿轮系统的拍击振动模型［J］.机械工程学报，2002，38(12):16-20.

ZHANG Suo-huai，SHEN Yun-wen，DONG Hai-jun，et al.Rattling model of a one-stage gear system ［J］.Chinese Journal of Mechanical Engineering，2002，38(12):16-20.

［13］ Shen Y J，Yang S P，Liu X D.Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method ［J］.International Journal of Mechanical Sciences，2006，48:1256-1263.

［14］申永军，杨绍普，潘存治，等.参外联合激励下直齿轮副的非线性动力学［J］.北京交通大学学报，2005，29(1):69-73.

SHEN Yong-jun，YANG Shao-pu，PAN Cun-zhi， et al.Nonlinear dynamics of a spur gear pair to parametric and externalexcitations ［J］. JournalofBeijing Jiaotong University，2005，29(1):69-73.

［15］刘国华，李亮玉，李培明，等.含间隙和时变刚度的齿轮系统非线性动力学模型的研究［J］.机械设计，2008，125(5):27-30.

LIU Guo-hua，LI Liang-yu，LI Pei-ming，et al.A study on nonlinear dynamics model of the gear system with clearance and time varying stiffness［J］.Journal of Machine Design，2008，125(5):27-30.