基于自依赖规则分析的主动规则终止性研究＊

陆惠玲，周 涛

（宁夏医科大学理学院，宁夏 银川750004）

1 引言

在主动数据库的研究中，主动规则是主动数据库的核心。主动数据库通过引入人工智能的知识控制理论检测数据库中的事件，当待检测事件发生后数据库会自动完成一系列的数据库操作，无须人为干涉。规则库是主动数据库的核心部分，是实现主动功能的基础［1，2］。规则主要由三部分组成：事件、条件、动作，包含有这些组件的规则称为事件—条件—动作ECA（Event Condition Action）规则，即在某一事件发生时引发数据库管理系统去检测数据库当前状态，看是否满足设定的条件，如果条件满足，便触发规定动作的执行。从规则的形式可以看出，一条规则的事件部分可以是另外一条规则的动作部分的子集，也就是说，一条规则的动作的执行同时也就意味着另外一条规则的事件的发生；同样，一条规则的条件部分依赖于对于当前数据库状态的查询，它的动作部分同时也在改变着当前数据库的状态，因而也就有可能使得另外一条原本条件为假的规则的条件部分变为真或者假。从上述分析可以看出，在一个规则库中，不同的规则的不同部分之间存在着影响和依赖。归纳起来，主动行为的复杂性主要体现在终止性和行为一致性方面［1，3，4］。由于规则的条件和动作执行结果依赖于它被处理时的数据库状态，无法仅仅根据规则的定义精确地判定对一组规则的处理必定是不可终止的或行为是不一致的。对于一个规则集合R，到目前为止能够判定规则终止性、汇流性的算法已经有很多，但从理论角度来讲都是不完备的。这也正是制约主动数据库发展的一个重要瓶颈。

文献［1］首先介绍了触发图的概念，在文献［5］中彻底阐述了这个概念：这样的一个图的建立依赖于规则的语法分析；图中的节点是规则，两条规则r1、r2通过一条从r1到r2的边连接（如果r1的动作包含规则r2的触发事件）。在这样一个图中环的存在意味着一种风险—规则集的非终止性。规则集合中如果不存在环就保证了规则集的终止性。然而该分析中没有考虑到规则的条件部分的惰化。因此，文献［1，6～9］从不同角度提出了规则终止性判断算法，整体来看就是考虑到了规则条件部分的惰化或者是一条路径上全部条件的惰化；文献［10］提出了一种方法来解开这个触发环，并考虑了一条路径上的所有条件都得到满足的情况；文献［11］精简了触发图，其中使用了partial和total边，这主要是考虑到了复合事件的影响。但是，主动规则的终止性问题仍然没有得到较好的解决，在主动规则的终止性分析方面的主要成绩就是提出了触发图以及在这方面的一些研究。

本文针对规则终止性问题展开讨论，通过分析触发边、活化边、惰化边三种边的触发时序关系，构造了条件断言函数来描述活化边和惰化边对ECA规则中条件的影响，最后给出了触发边、活化边和惰化边的组合时序对规则的具体触发情况；在此基础上进一步完善了Barakis R提出的不可归约规则集中的自依赖规则判定算法，对其中的能够形成环状结构的自触发规则给出了全面的讨论，提出了一种新的自依赖规则判定算法。该算法可以找到在不可归约集中由自触发规则引发的不终止性导致的一种环状触发，通过把自触发规则单独处理来打断这个环从而使规则集终止，有效提高了规则不终止性问题的判断能力。

2 基本概念

触发图TG（Triggering Graph）、触发边TE（Triggering Edge）、活 化 图 AG （Activation Graph）、活化边AE（Activation Edge）、惰化图DG（Deactivation Graph）和惰化边 DE（Deactivation Edge）是主动规则ECA分析的主要手段，其概念参见文献［1，11，12］。在惰化图中，大多数惰化边都是自惰化的，当然也有例外，特别是一个不包含条件成分的规则都是自惰化的。活化边和惰化边不会同时存在，即如果（Vri，Vrj）∈AE，则（Vri，Vrj）∉DE，反之亦然。在触发图中，文献［13］证明了触发环是规则非终止性的必要条件，如果TG中没有环，则规则执行必然终止。仅考虑TG图，相当于假定触发时条件为真，动作必然执行，TG环意味着非终止。引入AG图，触发环中没有到达活化边的规则在被触发时条件为假，动作不会执行，TG环未必导致非终止。进一步，引入DG图后，根据活化边与惰化边之间的相对次序，TG环中只含有到达活化边和惰化边规则在被触发时条件仍然可能为假，动作不会执行，仍可能判定终止。以下分析是基于TG、AG和DG的。

定义1 活化环：令AG＝（VR，AE）为一活化图，若有规则r1，r2，…，rk∈R，（r1，r2）∈AE，（r2，r3）∈AE，…，（rk，r1）∈AE，则称ρ＝（r1，r2，…rk）为一活化环。触发环是触发图中的环，活化环是活化图中的环。

定义2 条件断言函数Asseveration（G，r）：把关联图G中的活化边和惰化边对ECA规则r中条件的影响通过构造断言函数来表达。规定断言函数的返回值有True、False两个：如果规则r先被惰化，然后被活化（也就是说惰化边先到、活化边后到），那么条件断言函数的返回值为True；如果规则r先被活化，然后被惰化（也就是说活化边先到、惰化边后到），那么条件断言函数的返回值为False。还有两种特殊情况，一种就是只有一条活化边到达的情况，那么函数的返回值肯定为True；另外一种就是只有惰化边到达的情况，那么函数的返回值肯定为False。

为了在后面的算法中能够清晰地表达这种复杂的关系，仍然区分活化和惰化规则r的规则，称对规则r发出活化边的规则为条件断言函数的活化前件，称对规则r发出惰化边的规则为条件断言函数的惰化前件；可以简称为规则r的活化前件和惰化前件，而规则r称之为条件断言函数的后件。

可以用二叉树的形式来描述关联图中规则r与它的触发边、条件断言函数Asseveration（G，r）之间的关系。在二叉树中，节点代表规则，节点的左孩子代表它的事件依赖规则节点，节点的右孩子代表它的条件依赖（或逆条件依赖）规则节点，虚线表示条件断言函数，规则r1是规则r3的条件断言前件；实线表示触发边。如在图1中，r3条件依赖（或逆条件依赖）于r1，r2事件依赖于r1。

Figure 1 Binary－tree representation of association graph图1 关联图的二叉树表示

图1的邻接矩阵形式如图2所示。关联图中的规则数目决定邻接矩阵的规模，如果规则ri与规则rj之间存在触发边，则G［i，j］＝1；如果规则ri与规则rj之间存在活化边，则G［i，j］＝－1；如果规则ri与规则rj之间存在惰化边，则G［i，j］＝0。如果规则ri与规则rj之间不存在任何关系G［i，j］＝ ∞ 。

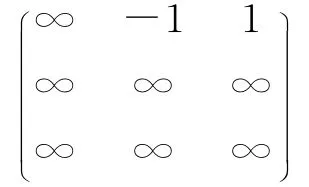
Figure 2 Storage structure of adjacency matrix 图2 邻接矩阵的存储结构

定义3 关联图（Association Graph）：令R 为任意规则集，TG（VR，TE）为触发图，AG（VA，AE）为活化图，DG（VD，DE）为惰化图，则G＝（VR，E）为关联图，其中E＝AE∪TE∪DE。

考虑规则ri的执行可能使规则rk的条件为真，规则rj的执行可能使规则rh的条件为假。在适当条件下，触发环和活化环未必导致规则集合呈现非终止性行为。在图3所示的例子中，按照文献［13］所述的算法，这个图是不可能规约的，判定为非终止的。若规则r3的执行使得规则r1的条件为假，则非终止性情况就会发生变化。在图3所示的例子中，加入惰化边（r3，r1）后得到图4，然后就可以很容易地判定它的终止性了。

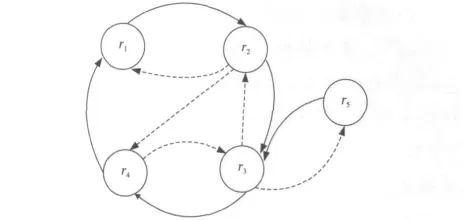
Figure 3 Non－termination analysis based on TGgraph and AGgraph图3 基于TG图和AG图非终止性分析

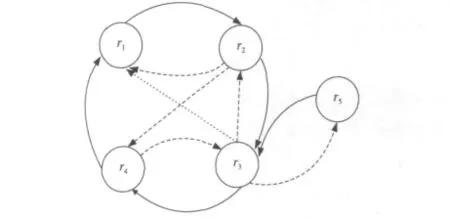
Figure 4 Termination analysis based on association graph图4 基于关联图的终止性分析

定义4 合格规则：设任意一条规则r∈R，如果该规则的条件部分为真，并且其所等待的事件已经发生，其发生的时刻不能早于条件为真的时刻，那么称这样的规则为合格规则。

关于这个概念要进行一些特别的说明，在一个关联图中存在三种依赖关系：事件依赖、条件依赖、条件逆依赖，它们分别与关联图中的三种边相对应，即触发边TE、AE、DE。活化与惰化的结果是使某条规则的条件为真或者为假，它们执行的结果可以在一段时间内有效，而触发行为却是瞬间的，其结果不能暂时保留，即对于一条ECA主动规则r，当事件发生时，如果条件C不晚于E被触发的时刻为真（也就是说这条规则的条件断言函数的返回值为真），那么规则r就是合格的。从另外一个角度来讲就是条件断言必须早于触发，这样的触发才有可能是有效触发，否则为无效触发。

定义5 自依赖规则：所谓自依赖规则，是指当一条规则r被系统调度执行以后，它的条件部分自动置为假，它的动作又触发和活化了规则库中的其它规则，从而产生了链锁反应。而经过了由于规则r的执行所导致的一系列的规则执行以后，r又成为可以被系统调度执行的合格规则（触发事件发生，规则r的条件断言函数返回值为真），称规则r为自依赖规则。

这个概念是文献［14］首先提出来的，并且在该文中给出了一个算法来判断在不可归约规则集中的自依赖规则。文献［14］指出，在规则不含优先级的情况下，多个被触发的规则的执行次序随意确定，其中必有呈现非终止性的排列，因而不可归约集会呈现非终止性行为；在规则包含优先级的情况下，多个被触发规则的执行次序由被触发规则的优先级确定，其排序次序唯一，如果该次序不导致终止行为的发生，则规则集仍然呈现终止行为。文献［4，20］给出进一步的讨论，如果归约以后规则集为空，说明该关联图中不存在环，这肯定是终止的。但是，这里需要说的是，上述结论不能推出如果关联图中存在环就一定不终止。换句话说，就是到目前为止能知道的是如果规则集终止就必须无环，但存在环未必不终止。经过归约以后的不可规约规则集就变成了许多个”环状”的规则集，分析这样的规则集的终止性是富有挑战性的一项工作。本文就是在这种情况下，在借鉴文献［14，15］的相关思想的基础上，对其中能够形成环状结构的自触发规则给出了详细的讨论，并通过一个算法找出了在不可归约集中的一种环，它是由自触发规则引发的不终止性。解决的办法就是把自触发规则单独处理以便打断这个环从而使规则集终止。显然这对规则的终止性分析有十分积极的意义。

3 自依赖规则的判定算法

3.1 自依赖规则的判定算法

在分析之前首先分析触发边、活化边、惰化边三种边的关系，以及它们的时序关系，前两种边代表的是可能，即如果某条规则被活化或触发，它有可能执行；惰化边代表肯定，即如果某条规则被惰化，那么这条规则肯定不能被执行。三种边的到达组合时序对规则r的触发影响，表1和表2给出了详细的说明。

Table 1 Combinatorial sequential relationship of two types of edges表1 有两种类型的边的组合时序关系

Table 2 Combinatorial sequential relationship of three types of edges表2 有三种类型的边的组合时序关系

说明：AE→TE表示AE的到达不晚于TE；把真正有意义的规则用加黑方式表示，并且在旁边加了＊。

规则r的条件断言活化前件、条件断言的惰化前件可能都不止一个，本文认为不管有几条活化边或者惰化边射入规则r，只要符合上面的几条时序关系，就与一条活化边或一条惰化边的效果是一样的，因此这里只考虑累计的效果。由于引入了条件断言函数，每次用条件断言函数来判断某条规则活化和惰化情况，而无须对有多条活化边或惰化边与只有一条活化边或惰化边的情况进行区分，这样惰化和活化被统一在了一个概念中，简化了终止性的分析。如果条件断言函数返回值为True，并且条件断言函数的执行早于触发边的到达，那么这条规则就可以被触发；如果条件断言函数返回值为False，并且条件断言函数的执行早于触发边的到达，那么在这种情况下，规则不能被触发，活化边是无效活化；如果条件断言函数返回值为False，并且条件断言函数的执行晚于触发边的到达，那么这条规则肯定不能被触发，也称为无效活化。当然如果只有活化边到达，则返回值肯定为真；如果只有惰化边到达，则返回值肯定为假。

3.2 算法基础

定理1 如果规则r是规则库中的一个自依赖规则，那么规则r必然在关联图中的一个触发环上［11］。

定义6 规则间的距离Dist（ri，rj）：在一个触发环中，两条规则ri与rj的距离是指在触发环中，ri到rj之间的弧的个数。

定义7 A（r）函数：r是关联图中的一个规则节点，函数的返回值是关联图中规则r的条件断言函数的活化前件ri（在条件断言函数的返回值为真的情况下），也就是说在关联图中存在着从ri到r的活化边。如果在关联图中，规则r没有条件断言函数活化前件，则返回值为0。

定义8 T（r）函数：r是关联图中的一个规则节点，函数的返回值是关联图中r的触发节点rj，也就是说在关联图中存在着从rj到r的触发边。如果在关联图中，r没有触发节点，则返回值为0。

定义9 在一个关联图中，一个规则节点r调用A（r）函数或者T（r）函数，如果返回值为0，那么规则r不是自依赖规则。

定义10 一条规则r的反向触发活化闭包记作r＊，定义如下：

（1）r0＝｛r｝；

（2）rn＝ ｛A（rn－1），T（rn－1）｝；

（3）r＊＝∪n≥0rn；

定义11 在关联图G中，如果规则ri是规则rj的条件断言函数的活化前件，并且规则rj的条件断言函数Asservation（G，rj）的返回值为真，那么，ri称作rj的直接活化节点，而ri的反向触发活化闭包中的所有规则节点，则称作规则rj的间接活化节点。

定义12 设r是一个触发环中的节点，如果r被调度执行以后不会被再次调度执行，称规则r是触发环中的一个断点。

定义13 规则r的直接或者间接活化节点调用函数T或者函数A，如果它的返回值为0，那么规则r不是自依赖规则。

定义14 将一条规则节点r的活化节点作为一棵二叉树的根节点，调用函数A，得到的规则节点ri作为r的右孩子节点，调用函数T，得到的规则节点rj作为r的左孩子节点，然后再对规则节点ri和rj调用函数T和A，得到的规则节点分别作为ri和rj的左孩子节点和右孩子节点，如此递归进行，从而形成了一棵二叉树，称这个过程为二叉树的形成过程。

定义15 在二叉树的形成过程中，作为具有同一父节点的兄弟节点，规定右孩子为活化节点，左孩子为触发节点，即右孩子对父节点起活化作用，称为间接活化节点的活化节点（根据二叉树形成的定义，二叉树的根节点是一个规则节点的直接活化节点，所以二叉树中的活化节点称作间接活化节点的活化节点），左孩子对父节点起到了触发作用，称为间接活化节点的触发节点。

定义16 在一棵二叉树中，节点e的路径长度是指从根节点到e之间的弧的个数。

定义17 在一棵以r1为根节点的二叉树T0（V0，E0，S0）中，令 T1（V1，E1，S1）为r1的左子树，在对T1进行中序遍历的过程中访问的最后一个节点，称作二叉树T0的左关键节点。

在图5中，T0的左关键节点是r5，因为对r的左子树的中序遍历的访问次序是：r4，r2，r5，其中r5是访问的最后一个规则节点。

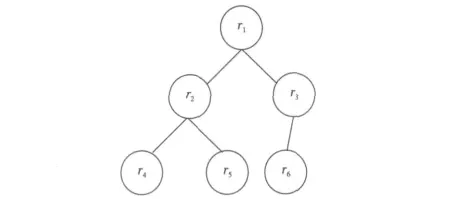
Figure 5 Key nodes graph图5 关键节点图

定义18 在一棵以r为根节点的二叉树T0（V0，E0，S0）中，令 T2（V2，E2，S2）为r1的右子树，在对T2进行中序遍历的过程中访问的最后一个节点，称作二叉树T0的右关键节点，称作二叉树T0的右关键节点。

在图5中T0的右关键节点是r3，因为对r的右子树的中序遍历的访问次序是r6，r3，其中r3是访问的最后一个规则节点。

定理2 如果一个触发环C上的规则节点r是自依赖规则，那么在对r的条件断言活化前件ri递归调用函数A和函数T所形成的二叉树中，必然会形成这样一棵二叉树，该二叉树的所有叶节点都落在触发环C上［16］。

定理3 在对一个关联图中的规则节点r递归调用函数A和函数T形成二叉树的过程中，如果新繁衍的叶节点是其祖先节点，则规则r不是自依赖规则［14］。

定理4 在触发环中的一条规则的条件断言函数的活化前件r对函数A和T的调用所形成的二叉树中，有两个具有同一父节点的兄弟节点ri、rj，若它们都是触发环中的节点且｜ri（或rj）的路径长度｜－｜触发环中rj（或rj）距r的距离｜≥0，则规则r不是自依赖规则［16］。

推论1 在由于对触发环中的规则r的函数A和T的递归调用所形成的二叉树中，有两个具有同一父节点的兄弟节点ri，rj。若它们都是触发环中的节点，且｜ri（或rj）的路径长度｜－｜触发环中rj到r的距离｜＜0，则规则r有可能不是触发环中的断点。

图6描述了一种简单的符合定理4的例子，下面来考察一下规则r1是否为自依赖规则。可以看到，规则r1由规则r9活化，即规则r9是规则r1条件断言活化前件，r2和r3是兄弟，它们既是二叉树中的节点，也是触发图中的节点。r1的执行导致了r2的执行，r2触发r3，r3活化r7，而r3的执行触发了r7与r4，此时，r4、r7同时合格，｜二叉树中r2的路径长度（为2）｜＜｜触发环中r3到r1的距离（为3）｜；r7和r8是兄弟，r7刚才已经分析过了，它不影响r1是否为自触发规则的判断，r8被r3活化，r3的路径长度为3，r8被规则r6触发，r6到r1的距离为1，即｜二叉树中r3的路径长度（为3）｜＞｜触发环中r6到r1的距离（为1）｜，在生成树中只要有一对具有相同父节点的节点满足条件，那么规则r1就可以断定不是自依赖规则。

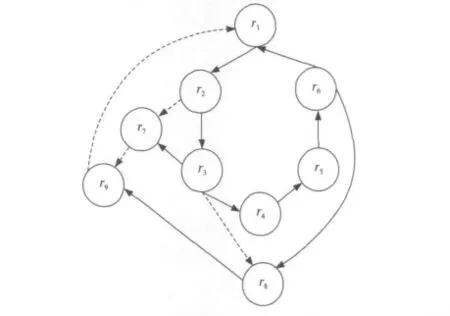
Figure 6 Relationship I between distance and path length图6 路径长度与距离的关系Ⅰ

在前面的叙述中其实已经说明了推论1的内容，虽然｜二叉树中r2的路径长度（为2）｜＜｜触发环中r3到r1的距离（为3）｜，但规则r1并不是自依赖规则，其原因在于在这棵生成二叉树中，并不是所有的具有相同根节点的节点都满足这一点，只要存在这么一对节点，都会导致节点r1不是自依赖规则。我们给出的定理4恰好就是基于这个假设的。

图7就是推论1的另外一种情况，对规则r1递归调用函数A和T得到一颗生成二叉树，可以看到，这棵二叉树中r2和r3具有同一个父节点r6，r2的路径长度为2，r3到r1的距离为3，规则r6是这棵二叉树中唯一的非终端节点，在这种情况下，规则r1就是自依赖规则。

定理5 对触发环中的节点r递归调用函数A和T得到的二叉树，叶节点都落在触发环上，在二叉树中，如果存在使同一个节点合格的左右子树的深度之差大于（触发环中）左子树最深叶节点与右子树中最深叶节点两者的距离，则规则r不是自依赖规则。

Figure 7 Relationship II between distance and path length图7 路径长度与距离的关系Ⅱ

证明 设二叉树中规则r的左右子树深度之差（｜左子树深度－右子树深度｜）为m，r的左子树叶节点的最右边的节点为rp（即r的左孩子中距根节点最远的节点），r的右子树叶节点的最右边的节点为rq（即r的右孩子中距根节点最远的节点），若使r合格的左右子树的深度之差＞（触发环中）左子树中最远的节点与右子树中最远的节点两者的距离＞0，则意味着触发环中r执行以后，右子树的rq首先合格，rq执行以后，触发环中rq节点的下一个节点rl合格，同时，二叉树中rq的父节点合格。根据拓扑关系，必须在rq的父节点和rl执行完毕之后才会考虑其它节点，又由于rq、rp的距离小于r的左右子树深度之差，所以r会在被激活之前被触发，因此规则r不会合格，进而可以推导出规则r不是自依赖规则。以上证明的是在触发环上rq＜Trp时的情况，而对于rp＜Trq时情况的证明与此类似。

证毕。

图8就是用来说明这种情况的，在触发环中，对r1递归调用函数A和函数T形成下面的结构，可见形成的二叉树其右子树比左子树深2，即｜deep（r5）－deep（r4）｜＝2，而在触发环中，dist（r4，r5）＝1，这说明当规则r1合格以后，在所有到达触发环的叶子规则中r4首先合格而被执行，r5在触发环中的距离（为2）肯定小于r4在二叉树中的路径长度（为4），所以规则r1肯定先被触发，后被活化，根据表1可知，这种触发属于无效触发。

所以规则r1不是自依赖规则。

3.3 自依赖规则判定算法

3.3.1 算法思路

下面给出判定一条规则是否是自依赖规则的算法思路：其实就是前面已经通过定义、定理的形式给出了各种不是自依赖规则的情况和是自依赖规则的情况，这里的算法思路就是前面内容的总结。

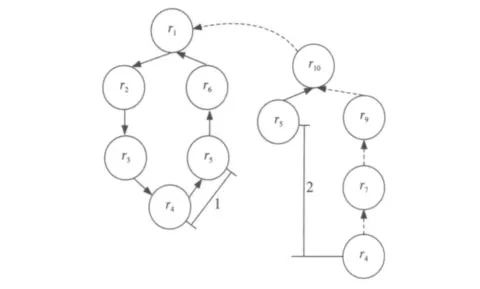
Figure 8 Relationship between depth differences of binary tree and distance of triggering ring图8 二叉树中的深度差与触发环中的距离的关系示意图

总体来说判断触发环中的一条规则r是否是自依赖规则可以分为三个阶段：

（1）在二叉树的形成过程中。

①在递归调用函数A和T形成二叉树的过程中，新繁衍生成的节点如果已经在前面生成，根据定理3，可知这里的二叉树中出现环状结构，则可以判定规则r不是自依赖规则。否则，规则r也不一定就是自依赖规则。

②在递归调用函数A和T形成二叉树的过程中，如果已经繁衍了n步，但还没有繁衍结束，根据定理6，可以判定规则r不是自依赖规则。否则，规则r也不一定就是自依赖规则。

（2）在二叉树生成后。

①如果生成二叉树的叶子节点不全落在触发环上，根据定理2可知该规则也不是自触发规则。

②逐一考察二叉树中的每一个非终端节点，如果其左、右子树的深度差大于其触发环中的距离，根据定理5，可以判定它不是自依赖规则。

③逐一考察二叉树中的每一个非终端节点，比较其左、右叶子节点的路径长度和距离。

如果右叶子节点的路径长度（活化）＜左叶子节点的距离，根据定理4判定规则r为自依赖规则。

如果右叶子节点的路径长度（活化）＞左叶子节点的距离，这仅仅是判定规则r是自依赖规则的必要条件，如果二叉树中的所有非终端节点全部满足这个条件，那么这个条件就变成了充分条件。根据推论4判定规则r为自依赖规则。否则，不是自依赖规则。

（3）其它情况。

如果一个触发环中已经判定其中一条规则已经是自依赖规则，根据定理7，可以判定触发环中的所有规则都是自依赖规则；反之也成立。

3.3.2 算法实现

算法1 自依赖规则的判定算法

输入 规则r、关联图（用邻接矩阵作为存储结构）

输出 如果规则r是自依赖规则，返回值是True，否则返回False。

步骤

（1）归约规则集

G＝CreatGraph（）；／／利用初始规则集构造一个关联图

R＝basic＿reduce（G）；／／对初始关联图进行归约

if R＝Øthen｛printf（“这个规则集是可归约的，是可以终止的”）；

return（True）；／／不存在自依赖规则｝；

else｛G＝CreatGraph（）；／＊然后利用归约以后的规则集再构造关联图＊／转步骤（2）；｝

（2）找到关联图G中的所有包含规则r的触发环

for i＝1 to｜R｜／＊｜R｜为归约以后规则集合中规则的

数目＊／

｛找第i个节点的所在的环，把找到的环添加到集合

Ui中，这里找到的环可能不止一个，｜Ui｜就表示集

合中的元素数目。｝

（3）生成二叉树并判定

num＝1；／／num用来统计繁衍的步数

for i＝1to｜R｜｛／＊分别用来判断每一条规则是不是

自依赖规则＊／

flag＝true；

for j＝i to｜Ui｜｛

num＝1；／／num用来统计繁衍的步数

U′i＝Ø；／／繁衍生成的节点集合

r′i＝ A（ri）；r′j＝ T（ri）；

while（r′i∉Uior r′j∉Ui）｛／＊当繁衍节点落到触发环则终止循环＊／

if r′i∉U′ior r′j∉U′ithen ｛flag＝False；return（False）；｝

else｛／＊把繁衍生成的节点添加到集合U′i中，并构造逻辑上的二叉树；＊／

num＝num＋1；

if num＞｜R｜｛flag＝False；return（False）；｝｝｝；

／／对生成的二叉树进行判定

if U′i＝Øthen return（False）；

else

for i＝1to｜U′i｜

if length（leftchild（ri））＜length（rightchild

（rj））｛falg＝False；return（False）；｝

／＊length函数用来计算节点的二叉树中节点的路径长度＊／

if｜length（r′i）－length（r′j）｜＞｜distance（r′i）－distance（r′j）｜ then ｛flag ＝ False；return（False）；｝

／＊r′i，r′j在 while循环结束以后保存的是刚才生成的二叉树的终端节点＊／

／＊distance函数用来计算二叉树终端节点在触发环中的距离＊／

if flag＝True break；／＊如果在当前正在判定的触发环中有一条规则是自依赖规则，则无需判定剩下的规则了，其它的全是自依赖规则＊／｝

4 结束语

ECA规则终止性问题是主动数据库中一个关键问题，在不可归约规则集中，如果归约以后规则集为空，说明该关联图中不存在环，这肯定是终止的。但是，上述结论不能推出如果关联图中存在环就一定不终止。换句话说，就是到目前为止能知道的是规则集如果想终止就必须无环，但存在环未必不终止。经过归约以后的不可规约规则集就变成了许多个”环状”的规则集，分析这样的规则集的终止性是富有挑战性的一项工作。本文就是在这样的一种情况下，在借鉴文献［14，15］相关思想的基础上，对其中的能够形成环状结构的自触发规则给出了详细的讨论，并通过一个算法找出了在不可归约集中的一种环，它是由自触发规则引发的不终止性。解决的办法就是把自触发规则单独处理以便打断这个环从而使规则集终止。显然这对规则的终止性分析是有十分积极意义的。

［1］ Baralis E，Widom J.An algebraic approach to rule analysis in expert database systems［C］∥Proc of the 20th International Conference on Very Large Data Bases，1994：475－486.

［2］ Hao Zhong－xiao.Theory of active database［M］.Beijing：Science Press，2009.（in Chinese）

［3］ Xiong Zhong－min，Hao Zhong－xiao.Determination of termination for a rule set based on conditional formula［J］.Journal of Harbin Institute of Technology，2009，41（5）：221－225.（in Chinese）

［4］ Hao Zhong－xiao，Xiong Zhong－min.An efficient algorithm for computing an irreducible rule set in active database［J］.Journal of Computer Research and Development，2006，43（2）：281－287.（in Chinese）

［5］ Vanduva A，Gatziu S，Dittrich K R.Investigating termina－tion in active database systems with expressive rule languages［C］∥Proc of International Workshop on Rule in Database Systems，1997：149－164.

［6］ Lee S Y，Ling T W.A path removing technique for detecting trigger termination［C］∥Proc of International Conference on Extend Database Technology（EDBT），1998：341－355.

［7］ Lee S Y，Ling T W.Unrolling cycle to decide trigger termination［C］∥Proc of the 25th VLDB Conference，1999：483－493.

［8］ Aiken A，Widom J，Hellerstein J M.Behavior of database production rules：Termination，confluence and observable determinism［C］∥Proc of the ACM SIGMOD International Conference on Management of Data，1992：59－68.

［9］ Lee S Y，Ling T W.Refined termination decision in active databse［C］∥Proc of International Conference on Database and Expert Systems Application（DEXA），1997：182－191.

［10］ Bailey J，Dong G，Ramamohanarao K.Deciability and undecidability result for the termination problem of active databases［C］∥Proc of the 17th ACM SIGMOD－SIGACT－SIGART Symposium on Principles of Database Systems，1998：264－273.

［11］ Wang Rui－xiang.Dependency problem of active database［D］.Qiqihar：Qiqihar University，2003.（in Chinese）

［12］ Yan Wei－min.Data structure［M］.Beijing：Tsinghua University Press，1999.（in Chinese）

［13］ Baralis E，Ceri S，Monteleone G，et al.An intelligent database system application：The design of EMS［C］∥Applications of Database LNCS，1994：172－189.

［14］ Barakis R，Ceri S，Paraboschi S.Improved rule analysis by means of triggering and activation graph［C］∥Rules in Database Systems，Lecture Note in Computer Science，1995：165－181.

［15］ Zuo Wan－li，Liu Ju－hong，Liu Shu－fen.Relationship graph and termination analysis for active rules set［J］.Journal of Software，2001，12（2）：276－282.

［16］ Zhou Tao.Active rules design and analysis of active database in object－oriented database［D］.Qiqihar：Qiqihar University，2004.（in Chinese）

［17］ Karamimce A P，Urban S D.Refined triggering graph：A logic－based approach to termination analysis in an active object－oriented database［C］∥Proc of the 12th International Conference on Data Engineering（ICDE），1996：384－391.

［18］ Baralis E，Ceri S，Paraboschi S.Improved rule analysis by means of triggering and activation graph［C］∥Proc of International Workshop Rules in Database Systems（RIDS），1995，985：163－181.

［19］ Aiken A，Hellerstein J M，Widom J.Static analysis techniques for predicting the behaviour of active database rules［J］.ACM TODS，1995，20（1）：3－41.

附中文参考文献：

［2］ 郝忠孝.主动数据库理论基础［M］.北京：科学出版社，2009.

［3］ 熊中敏，郝忠孝.基于条件公式的主动规则集可终止性判定［J］.哈尔滨工业大学学报，2009，41（5）：221－225.

［4］ 郝忠孝，熊中敏.计算主动数据库中不可归约规则集的有效性算法［J］.计算机研究与发展，2006，43（2）：281－287.

［11］ 王瑞祥.主动数据库中的依赖问题［D］.齐齐哈尔：齐齐哈尔大学，2003.

［12］ 严蔚敏.数据结构［M］.北京：清华大学出版社，1999.

［16］ 周涛，面向对象的主动数据库中主动规则的设计和分析［D］.齐齐哈尔：齐齐哈尔大学，2004.