基于GM(1,1)-Markov链模型的汽车企业订单预测
2013-09-08李西兴徐增师
李西兴,徐增师
(武汉理工大学机电工程学院,湖北武汉 430070)
随着中国汽车市场经济的繁荣发展,汽车制造商之间的竞争也变得越来越激烈。准确地分析和预测订单数量对于汽车制造商商业模式的优化、商机的把握和产品竞争力的提高有着重要意义。
常用的分析和预测方法有回归分析法、弹性系数法、指数平滑法和移动平均法[1]。对于不同的分析和预测方法,根据数据要求的多样性从复杂的样本数据中提取出准确信息所采用的方法是不同的。作为潜在的新型市场产业,汽车产业已经成为影响国家经济发展与规划、产业政策转型和人民消费水平的重要因素,但由于缺乏准确的基础信息数据,汽车产业的潜在发展趋势还不能很准确地预测。1982年由邓聚龙提出的灰色预测理论,可在信息不确定和不充分的环境下,通过运用少量数据作出较准确的预测[2]。
因此,目前有许多研究人员都通过采用灰色预测理论来提高预测能力,虽然灰色预测理论已在许多领域得到成功应用,但研究表明该预测方法还可进一步改善。基于灰色系统理论,通过对某一企业汽车销售数量运用Markov链预测方法,得到了改进的GM(1,1)-Markov链模型的订单预测,即通过负时间序列产生的累积数据序列减少或消除在建立GM(1,1)模型时所用到的参数设置,研究结果表明了该预测方法的可靠性。
1 改进的GM(1,1)模型
由邓聚龙提出的灰色预测理论最初是用来通过对系统(该系统通常数据少、信息不足且不确定)原始数据的处理和灰色模型的建立来帮助系统做出一个科学的、定量的预测[3]。累加算子(accumulating generation operator,AGO)和逆累加算子(inverse accumulating generation operator,IAGO)是灰色理论中两个重要的数据处理方法。累加算子(AGO)通过转换原始数据的类型发现它们的内在规律并作出预测,逆累加算子(IAGO)再将预测输出转变回原来的状态。这些数据的处理方法对于预测模型的准确性起着决定性作用。灰色预测理论有着样本数据要求少、计算简单和短期预测精度高等优点,因此得到了广泛应用并取得了理想的成果。但是与其他的预测理论一样,灰色预测理论也有自己的局限性,其要求原始数据的阵列具有较高的柔性。通过对原始数据阵列的处理和幂函数变换可以提高原始数据阵列的柔性[4]。
构建GM(1,1)模型的常规步骤如下:
(1)首先假设原始数组X(0)={x(0)(1),x(0)(2),…,x(0)(n)},并且 x(0)(k)≥0,k=1,2,…,n。

(3)建立灰度微分方程。通过最小二乘法估算灰色控制变量参数a和b,建立灰色微分方程,GM(1,1)模型的一阶微分方程为:

通过最小二乘法将参数a和b转换为:
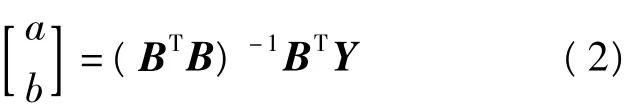
其中,常数向量Y为:
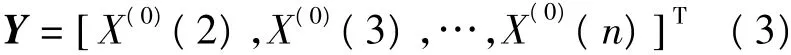
同时累计矩阵B为:

其中,Z(1)(t)=[x(1)(t)+x(1)(t-1)]/2,t=2,3,…,n。
(4)获取相应值x(0)(t+1)。灰色模型GM(1,1)的时间相应函数由微分方程的解得到:

灰色模型GM(1,1)的时间响应函数可以由式(6)微分方程取代:
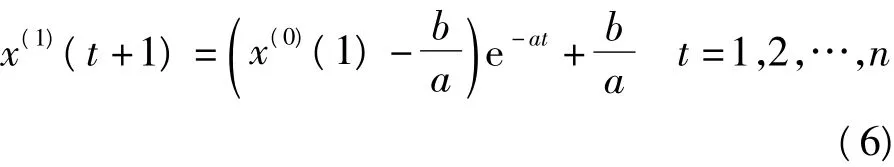
假设x(1)(1)=x(0)(1),一阶序列逆累加算子(IAGO)可以还原为:
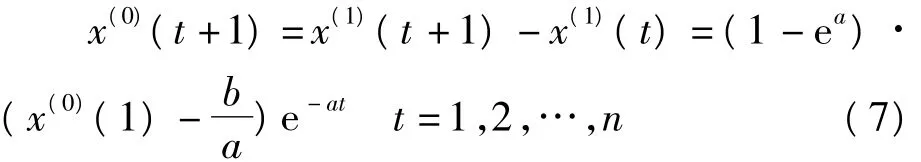
由于原始数据本身的波动性,数据独立的随机性和混沌性,以及某些原始数据的局限性,很难将预测范围定格在一个较小的范围内,这样就导致了在大多数的案例分析中灰色模型显得不那么精准。由于灰色模型要求原始数据具有较高的柔性,在逆累加算子(IAGO)输出数据之前应规定性能参数,这样才能将其应用到微分方程中。然而,相比于以前的GM(1,1)模型函数建立过程,改进的GM(1,1)模型函数在建立时,通过负时间序列产生的累积数据序列减少或消除了这些参数设置,从而使得这种情况下的幂函数变换提高了原始数据处理阵列对原始数据柔性的处理效果[5]。
假设原始数据阵列{x0(n)}是一个不光滑的离散的数据阵列,用幂函数变换的方法来转换阵列{xn(t)},得到一个新的更加平滑的数据阵列,这个新阵列用于帮助接下来的分析预测,最后采用将预测输出转换成原始数据状态。
2 Markov链模型
根据过渡矩阵,Markov链描绘出一个模块领域在未来的一段时间内经济发展转变的趋势并反映出了它的制度规则[6]。Markov链状态转移矩阵可以提供对下一周期预测值的一种潜在的更正预测。由于汽车销售数量在未来是一个随机波动的数据,并且预测系统是一个随机动力系统,因此该研究采用Markov链预测可以较好地提高预测的准确性。
在建立状态转移矩阵之前应该将模块划分,参照Markov链的性质,对于任意一个模块都可以划分为n个小模块,并且每个小模块都满足以下等式[7]:
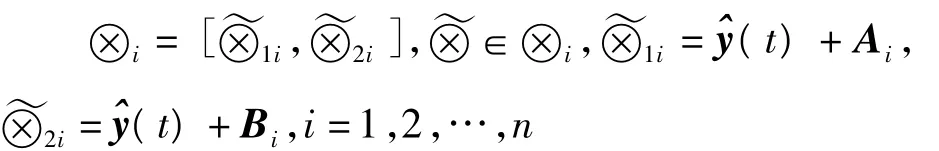
其中:⊗i为任意一个小模块中的子级分模块;分别为任意子级模块的区间上下限;为常数向量;Ai、Bi为不同参数矩阵。
假设Mij(m)是原始样本数据通过m次转换,从模块⊗i到模块⊗j的转换数量,Mi是在模块⊗i条件下的原始样本数据的总数,然后通过Pij(m)的组合构成了矩阵P(m),矩阵P(m)称为Markov链的k步转移概率矩阵[8-10],如下所示:
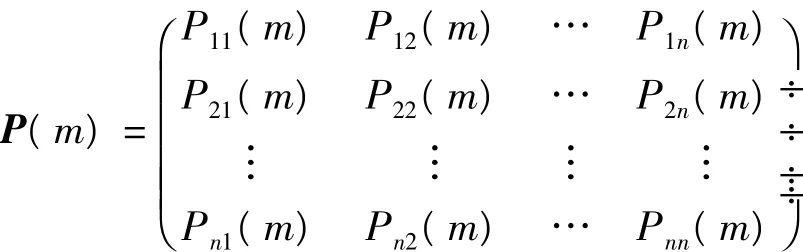
并且 Pij(m)=Mij(m)/Mi,i=1,2,…,n,是指通过m步从模块i到模块j的转换。假设预测对象是在模块i下,计算出矩阵P(m)中k步的概率,如果,可以认为在下一周期中模块转移概率最有可能发生在模块⊗k到模块⊗1的转换中。
3 GM(1,1)-Markov链模型的应用
该测试研究对象为柳州市一家汽车公司,参考分析数据为2011年3月到10月的实际销售数量(如表1所示),同时表1给出了通过原始的基于灰色理论的GM(1,1)模型得到的预测值,由表1可知GM(1,1)模型的平均精度达到94.8%。

表1 实际销售数量与基于GM(1,1)模型的预测量
用Markov链来修正表1预测值,得到实际销售量与基于改进的GM(1,1)-Markov链模型的预测量如表2所示。通过运用Markov链,可以得到实际订单量和预测订单量的差别,计算得出此时的平均预测精度达到了97.5%。基于优化的GM(1,1)模型和Markov链模型,订单预测精度取得了进一步提高。由于篇幅问题,具体的计算过程不再详述。

表2 实际销售量与基于改进的GM(1,1)-Markov链模型的预测量
通过表1与表2的对比,不难发现在运用改进的GM(1,1)-Markov链模型对销售数量做预测相对于原始的基于灰色理论的GM(1,1)预测其准确性得到了提高。
4 结论
该研究提出了基于改进的GM(1,1)-Markov链模型的一阶订单销售数量的预测方法,即通过负时间序列产生的累积数据序列减少或消除在建立GM(1,1)模型时所用到的参数设置,该模型继承了GM(1,1)模型和Markov链模型的演变规律,即时间序列数据和随机事件数据通过状态转移概率矩阵的转换,使得预测结果更加可靠。该预测模型提高了预测值的准确度,同时为公司的产品生产订单提供了合理的预测。然而受到诸多不确定性因素的影响,该预测模型对于短期内的预测效果较好,但对于长期的预测结果还有待改进。
[1]刘思峰.灰色系统理论及其研究[M].北京:科学出版社,2010:50-98.
[2]WU C R,CHANG C W,LIN H L.A forecast model for evaluating physicians'supply and demand in the Taiwanese remote islands[J].J Grey Syst,2009(21):25-34.
[3]邓聚龙.灰色控制系统[M].武汉:华中理工大学出版社,1993:9-76.
[4]刘志谦,宋瑞.基于GM(1,1)-Markov链的城市汽车保有量预测研究[J].交通与安全,2008,8(2):33-36.
[5]何霞,刘卫锋.灰色 GM(1,1)模型的改进及应用[J].江南大学学报:自然科学版,2011,3(3):233-236.
[6]李朝阳,魏毅.基于Matlab灰色GM(1,1)模型的大气污染物浓度预测[J].环境科学与管理,2012,1(8):16-20.
[7]石留杰,李艳军,臧雨婷,等.基于 GM(1,1)-Markov模型的我国人口城市化水平预测[J].四川理工学院学报,2010,12(9):399-402.
[8]LI D C ,CHANG C J.An extended grey forecasting model for omnidirectional forecasting considering data gap difference[J].Applied Mathematical Modeling,2011(35):5051-5058.
[9]XIE N M,LIU S F.Discrete grey forecasting model and its optimization[J].Apply Math Model,2009(33):1173-1186.
[10]TSAUR R C,LIAO Y C.Forecasting LCD TV demand using the fuzzy grey model GM(1,1) [J].Int J Uncertainty Fuzziness Know-Based Syst,2007(15):753-767.
