基于多工况并行任务的摩托车悬架参数多目标优化

徐中明，杨建国，张志飞，李仕生，李晓灵

(1.重庆大学 机械传动国家重点实验室，重庆 400030;2.重庆大学 机械工程学院，重庆 400030;3.重庆建设摩托车股份有限公司，重庆 400054)

摩托车悬架系统是整车的重要组成部分，对整车的行驶平顺性、操纵稳定性、骑乘的舒适性等有着很大影响［1］。用户对摩托车综合性能要求的不断提高，国内外对摩托车悬架系统的研究越来越受到重视。当前国内外对摩托车悬架系统的研究较多的集中在悬架系统零部件性能改善［2－3］、单一工况下的性能提升等方面，从人－车系统和整车综合性能角度对悬架系统进行设计研究的还较少。在平顺性方面，当前大部分研究都是以随机路面工况下降低垂向振动为目标［4－5］，并没有考虑俯仰振动的影响，由于摩托车的悬挂质量分配系数ε远小于1，前后悬架系统具有高度的耦合性，因此，车身局部垂向振动的改善可能导致俯仰振动的加剧，从而使整车舒适性变差;此外，随机路面工况下平顺性的改善可能导致其它工况下舒适性的降低，由于摩托车前悬架刚度较小，加速制动时俯仰角太大会导致前叉管撞击限位，从而影响整车舒适性。半主动悬架能够适应复杂多变的行驶工况，对于改善摩托车的垂向和俯仰振动能够取得良好的效果［6－8］，并且能够保证其它工况下的整车舒适性，但由于成本昂贵，在摩托车上的应用受到限制，目前在国内的摩托车上未见使用。俯仰和垂向振动是影响车辆乘坐舒适性的关键问题［9］，国内外从考虑俯仰振动角度对摩托车平顺性研究的文献很少，而从多工况角度对摩托车悬架系统进行匹配研究的文献还未有报道。

本文针对某125摩托车存在的制动俯仰角过大的问题对悬架系统进行优化匹配，通过悬架特性参数的合理匹配实现制动俯仰角的降低，避免发生前悬架撞击限位提高骑乘舒适性，同时保证随机路面工况下的平顺性能。采用摩托车动力学专用软件BikeSim建立包含驾驶员在内的人－车系统仿真模型，以加速/制动工况下的车身俯仰角最大值和B级路面工况下的俯仰、垂向振动加速度均方根值为优化目标，在iSIGHT中建立两种工况的并行优化任务，集成BikeSim、MATLAB进行多目标优化，取得了明显效果。

1 加速/制动与平顺性仿真

1.1 BikeSim中人－车系统模型的建立

整车模型的建立。BikeSim是一种基于数学模型的面向特性的参数化建模的动力学软件，该模型共包含10个刚性体29个自由度，将整车分为车体、转向、轮胎、悬架、制动、传动等子系统，通过输入各子系统的特性参数或曲线进行建模，其整车模型如图1所示。

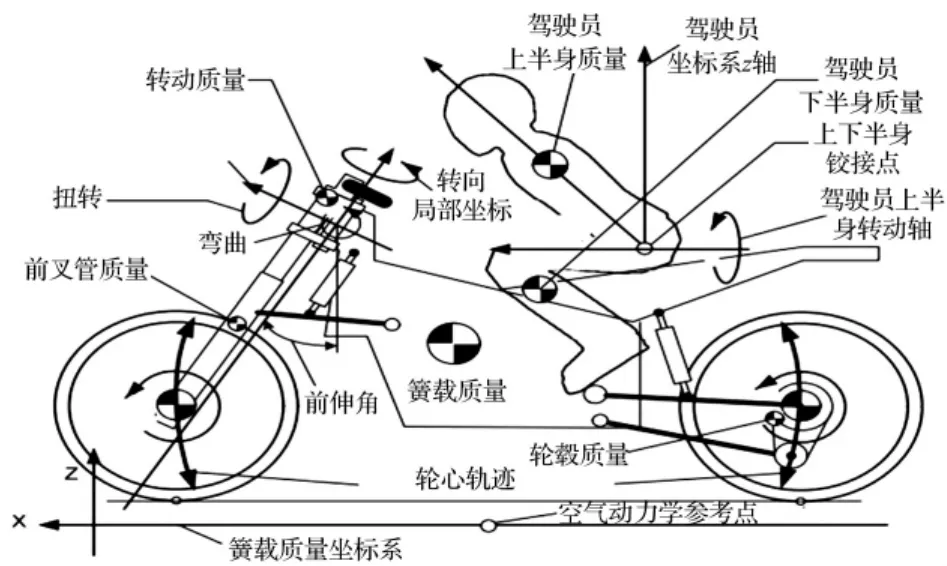
图1 摩托车整车模型Fig.1 Vehicle model of motorcycle

由于摩托车后悬架结构形式多样，BikeSim将后悬架统一简化为摇臂机构，通过摇臂杠杆比来表达不同的悬架结构。对于制动系，BikeSim用杠杆比来表达制动操纵机构，将操纵机构对制动系输入的制动力简化为制动杠杆力，制动杠杆力经过增压器、主缸、比例阀、轮缸等一系列部件的传递作用最终形成车轮上的制动力矩，由于本文只是研究相同制动力条件下不同悬架特性参数的车身俯仰角，只需制动系产生相同的减速度，因此制动系可采用BikeSim自带的制动系模型。BikeSim提供的轮胎模型包括:“魔术公式”、查表轮胎模型和第三方轮胎模型，本文采用的是“魔术公式”。整车模型中制动系、传动系和轮胎对本文的研究不产生影响，考虑到单独建模的复杂性，这里采用了BikeS-im自带的模型，其他子系统均是根据对象车的实际结构提取的参数建立。建立的某125摩托车部分参数如表1所示。

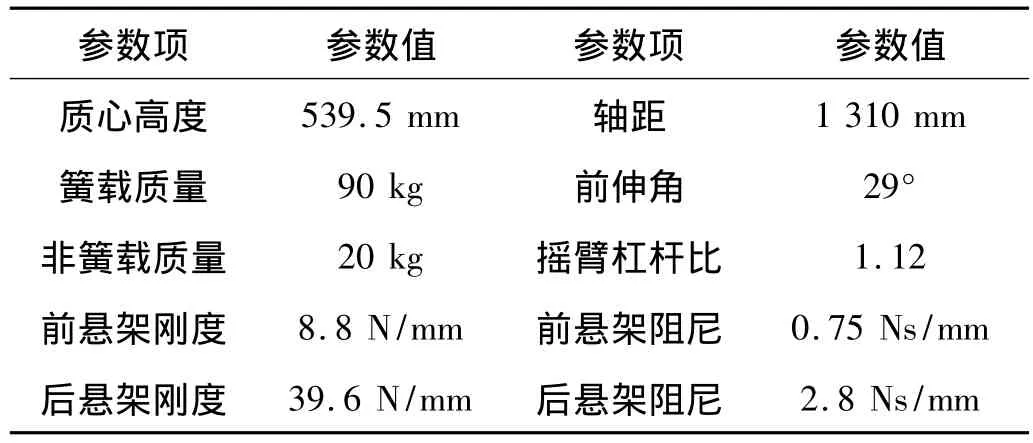
表1 某125摩托车部分参数Tab.1 Some parameters of a 125 motorcycle

驾驶员模型的建立。由于摩托车驾驶员的质量与摩托车整备质量相当，因此在整车建模时必须考虑驾驶员的影响。当前大部分研究中对于驾驶员模型过于简化，并不能全面的反映整车动力学特性;有的甚至忽略了驾驶员的影响，不符合真实情况。BikeSim中将驾驶员质量分为上下半身两部分，考虑了上下半身的质量、转动惯量、尺寸、姿势等关键因素，上下半身通过转动副连接，上半身可以相对于车架做侧倾和侧向运动。按照NASA的建议驾驶员上半身质量占62%，下半身质量占38%进行质量分配。这里取驾驶员质量为70 kg，建立的驾驶员模型如图2所示。

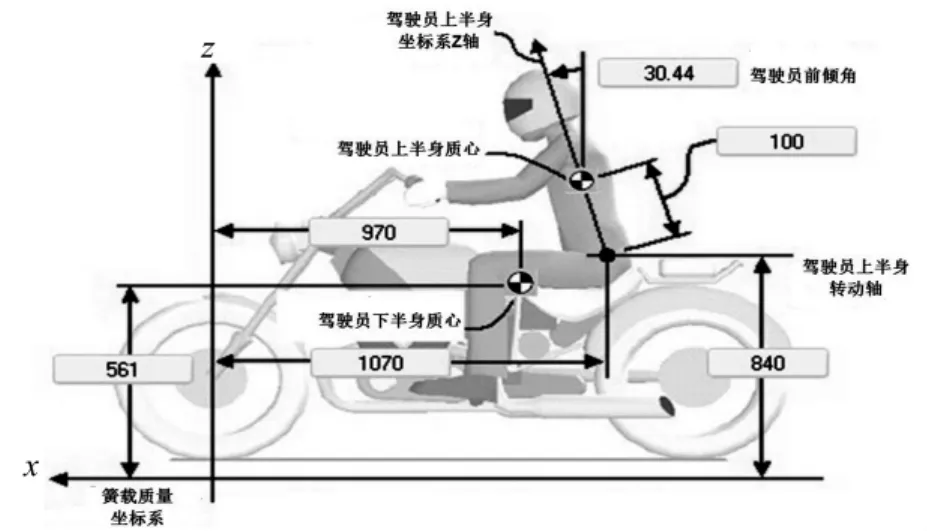
图2 驾驶员模型Fig.2 Driver model

1.2 路面模型的建立

加速制动仿真路面的建立。在BikeSim的道路建模部分根据GB20073的要求建立平直路面，设置道路附着系数为0.85，建立的平直路面如图3所示。

图3 平直路面Fig.3 Flat straight road model

平顺性仿真路面的建立。摩托车是单轨车辆，平顺性仿真时只需在BikeSim中建立道路高程随路长变化的二维路面模型。按照GB/T7031对于道路分级的要求以及道路平度的表示方法，本文采用谐波叠加法［10－11］对 B级路面的平度进行模拟。

式中:θ为［0，2π］上的随机数;x为道路的x方向。通过离散道路x方向的值，就可以得到随机路面z方向的值。

根据以上原理，采用MATLAB编制B级路面程序，得到的B级路面的平度数据导入BikeSim中，如图4。

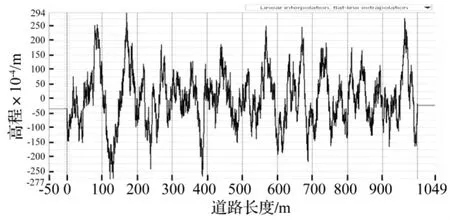
图4 B级路面不平度Fig.4 Grade B road stochastic excitation

1.3 加速/制动工况的设定与仿真计算

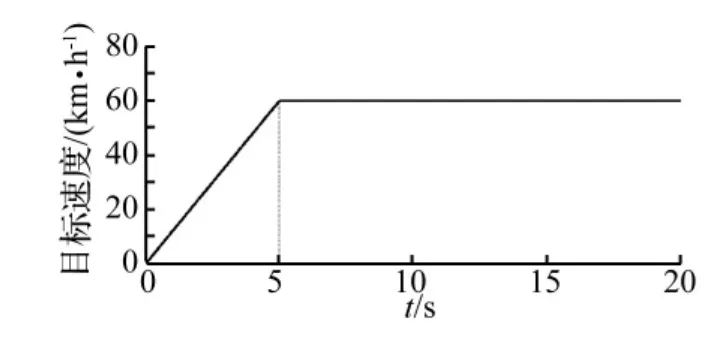
图5 速度变化曲线Fig.5 Target speed curve

在平直路面上进行加速/制动工况的仿真，加速工况设定为0～5 s速度从0均匀增加到60 km/h，之后进入匀速行驶;从第15 s开始制动，为了获得更好的制动效果，采用联动制动的方式给前后轮同时添加制动力。作用在摩托车上的制动力的大小与众多因素有关，包括操纵机构的杠杆比、液压传动系统、地面附着情况等，但制动力与制动系统并非本文研究重点，这里只是为了在附着良好的情况下获得满足要求的制动加速度，因此只要添加合适的制动力即可。在BikeSim中需要添加的是制动杠杆力(即制动踏板力与杠杆比的乘积)，不需要考虑复杂的制动操纵机构，这里给前后轮添加的制动杠杆力分别为120 N和80 N。速度和制动力曲线如图5、图6。

设定仿真时间为25 s，运行仿真，得到的速度、俯仰角和前后悬架变形曲线如下图所示。虽然制动时俯仰角加速度也会对行驶舒适性产生一定影响，但是由于俯仰角加速度主要受制动力大小的影响，悬架特性参数的改变对其降低效果并不明显，因此，这里没有给出俯仰角加速度的曲线。

从图7可以发现，在制动力作用下17.5 s时速度降低为0，前进已经停止，计算可知制动减速度大小为6.67 m/s2，完全满足GB20073对于L3类摩托车制动性能的要求，说明添加的制动杠杆力大小是合适的。

从图8可以看出加速阶段俯仰角较小，俯仰角最大值出现在制动即将停止时，最大值为6.4°，制动阶段的车身俯仰运动近似于整车绕后轴的旋转，会导致前叉管发生压缩运动，由图9可以看出前叉管压缩最大值为199.7 mm，而前叉管的行程仅为105 mm，因此必然会发生撞击限位而影响整车的骑乘舒适性。

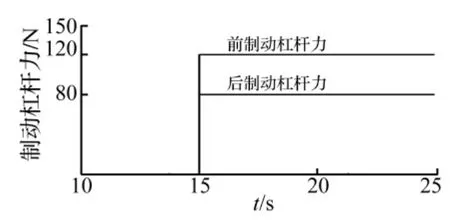
图6 前后制动杠杆力曲线Fig.6 The front and rear break lever forces

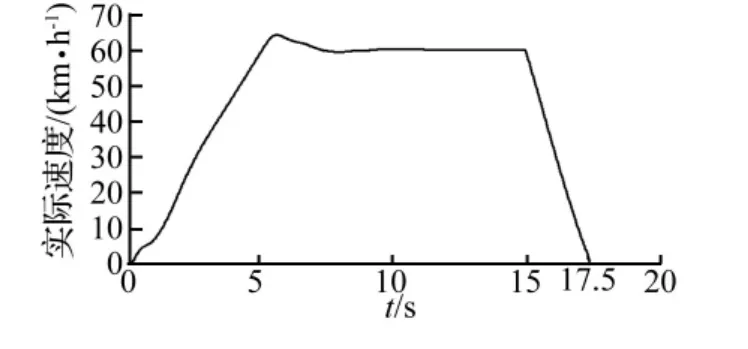
图7 加速/制动时速度曲线Fig.7 Speed curve during acceleration-braking

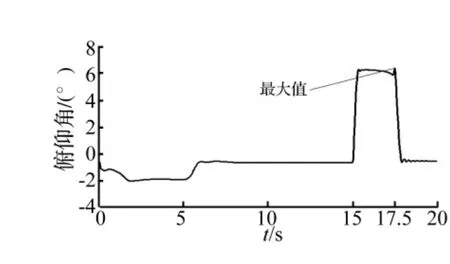
图8 加速/制动时俯仰角曲线Fig.8 Pitch angle curve during acceleration-braking

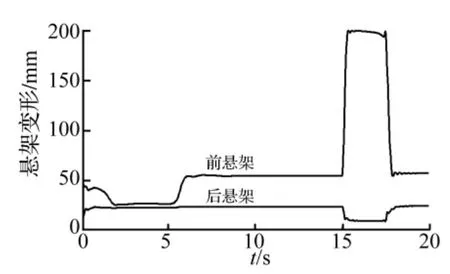
图9 加速/制动时前后悬架变形Fig.9 Suspension deformation during acceleration-braking

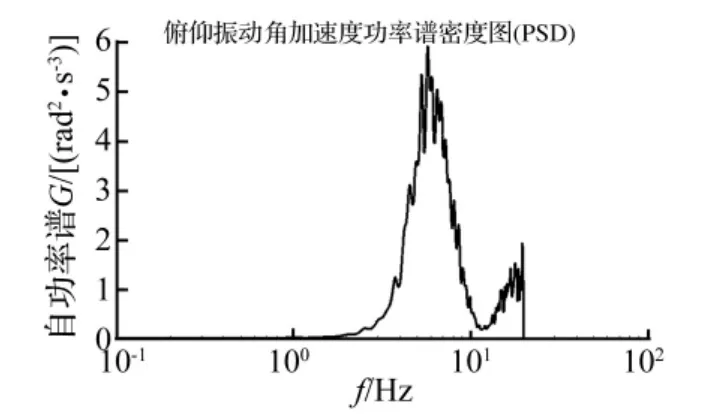
图10 车身俯仰振动角加速度功率谱密度Fig.10 PSD of body pitching vibration acceleration

1.4 平顺性工况的设定与仿真计算

B级路面下的平顺性仿真。设定摩托车以车速60 km/h等速行驶于B级路面上，仿真时间90s，将计算结果导入MATLAB进行后处理得到俯仰和垂向振动加速度均方根值分别为 5.12 rad/s2、1.69 m/s2，图 10、图11分别是车身俯仰、垂向振动加速度功率谱密度。

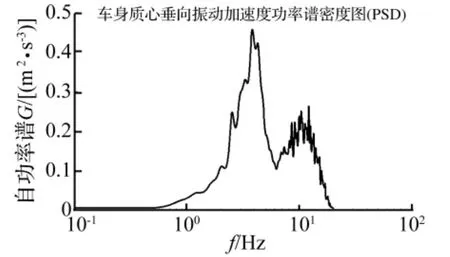
图11 车身质心垂向振动加速度功率谱密度Fig.11 PSD of sprung mass vertical vibration acceleration

2 多工况并行任务多目标优化的实现

2.1 问题描述

为了实现该车在加速/制动时行驶舒适性的改善，避免前叉管撞击限位，同时保证随机路面的平顺性，防止俯仰或垂向振动的恶化;以前、后悬架的刚度、阻尼为设计变量，以加速/制动时俯仰角最大值和随机路面工况下车身质心俯仰、垂向振动加速度均方根值为优化目标，采用NSGA－Ⅱ算法进行多目标优化。通过前后悬架的刚度、阻尼的优化匹配实现该车在这两种工况下综合性能的提高。

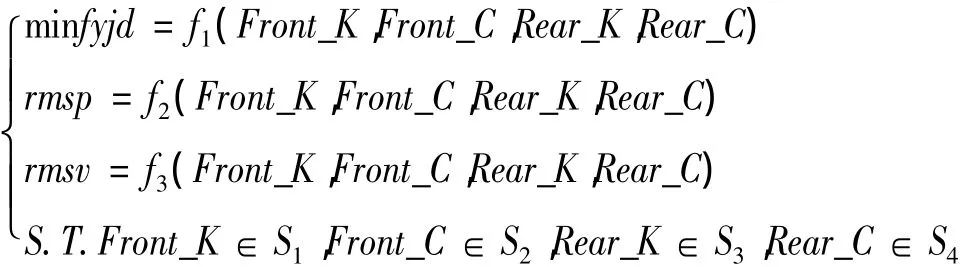
该优化问题的数学模型可描述为:式中:fyjd是加速/制动工况下俯仰角最大值，rmsp、rmsv分别是俯仰和垂向振动加速度均方根值，Front_K、Front_C、Rear_K、Rear_C分别是前、后悬架的刚度、阻尼。

2.2 多工况并行任务优化平台的搭建

BikeSim具有开放的接口，可以与多种软件连接实现联合仿真优化。本文的多目标优化平台的搭建采用专业的优化软件iSIGHT通过接口技术集成BikeSim来实现，为了处理仿真计算过程中产生的大量数据，这里采用MATLAB编写数据处理程序，并集成到iSIGHT中实现数据的自动化处理。在这三个软件的集成中，BikeSim负责不同工况的仿真，MATLAB负责数据处理，iSIGHT的优化控件提供优化算法并驱动BikeSim和MATLAB实现迭代计算。每一次计算过程中，优化控件给出的一组悬架特性参数将同时传递给加速/制动工况和B级路面工况，两种工况将同时开始仿真，形成并行计算任务。建立的并行任务优化工作流程如图12，并行任务的计算结果将同时传递给优化控件。

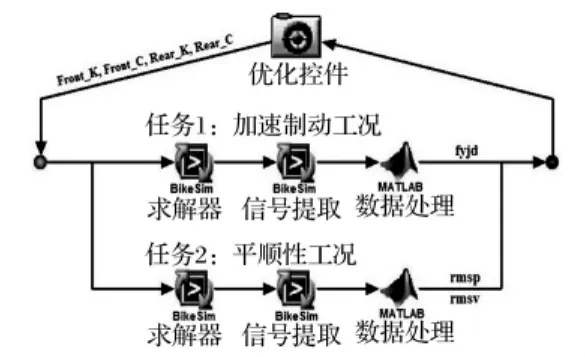
图12 并行任务优化工作流程Fig.12 The workflow of parallel optimized tasks

iSIGHT驱动BikeSim和MATLAB进行联合仿真优化，能够使各个软件发挥专长使优化计算的精度和效率都极大提高。

2.3 参数设置与计算

本文以摩托车前后悬架的刚度和阻尼作为设计变量。由于摩托车的悬挂质量分配系数ε远小于1，与轿车的差别较大，前后悬架系统耦合紧密，因此不宜采用偏频法来确定前后悬架刚度的取值范围。这里是根据悬架的静挠度来确定刚度的上下限的，在BikeSim中通过在静平衡时悬架变形量在一定范围内来确定刚度的上下限，阻尼的上下限按照与刚度初始值扩大相同的比例来确定。这里将表1中悬架原始特性参数值作为设计变量初始值，初始值和上下限如表2。

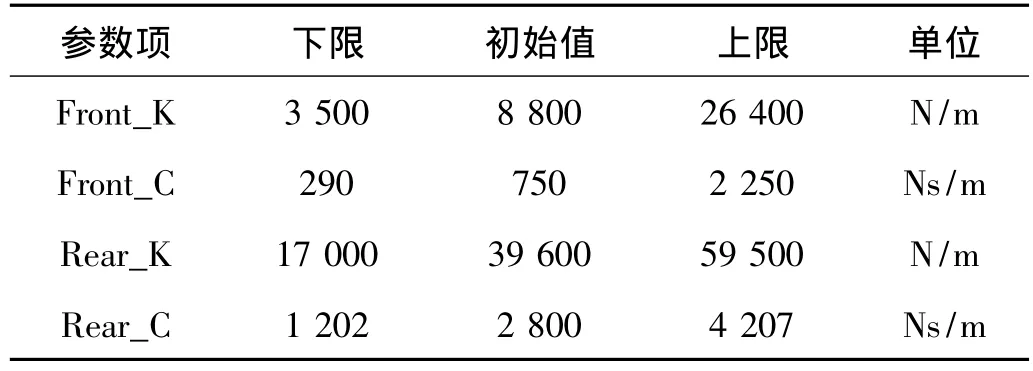
表2 设计变量参数表Tab.2 The list of design variables

在平顺性工况中，由于悬架动挠度的增大会使撞击限位的概率增大，使平顺性变差，因此在优化的同时必须对前后悬架的动挠度进行约束。一般要求为:

式中:fd1，fd2分别为前后悬的动挠度;［fd1］=50 mm，［fd2］=25 mm分别是前后悬的限位行程。

遗传算法具有鲁棒性、全局最优性、高效并行性、不要求函数连续可导等特点，近年来在车辆悬架方面的应用越来越多［12］，然而基本遗传算法只适用于传统的单目标优化问题。对于本文的多目标优化问题，采用iSIGHT提供的NSGA－Ⅱ算法来实现，设定种群数量50、遗传代数50、交叉率0.9。

经过2 500次计算，得到的计算结果如图13所示，将计算结果向坐标平面投影可以得到图14、图15，从图中可以看出计算结果已收敛，在两个坐标面上Pareto前沿已经形成，由多目标优化的基础理论可知Pareto前沿是各种权重下最优值点的集合，从计算结果可以发现两个Pareto前沿分别近似为直线段。

3 优化计算结果分析

3.1 目标权重与最优值的确定

多目标优化的最优值是针对某一权重下的最优值，为了找出最优值首先要确定目标权重。但是先决策后寻优的模式无法准确把握目标权重，该模式在应用中存在明显的缺陷，本文采用的是先寻优后决策的模式［13－14］。由多目标优化的基础理论可知:多目标优化的最优值通常存在于Pareto前沿上。因此本文根据计算得到的Pareto前沿的特点来确定权重关系。从图14、图15可以看出两个图中的Pareto前沿近似为直线，通过数据拟合可以得到Pareto前沿的斜率，Pareto前沿的斜率反映了目标之间的权重关系。

设加速/制动工况下俯仰角最大值fyjd的权重为P;等速B级路面工况下俯仰振动加速度均方根值rmsp的权重为M，垂向振动加速度均方根值rmsv的权重为N。在rmsp－fyjd平面上，通过数据拟合可知Pareto前沿的斜率为 －0.39，为了计算方便这里取 －0.4。同样，在rmsv－fyjd平面上得到的 Pareto前沿斜率为－0.83，这里取 －0.8，即权重关系为:

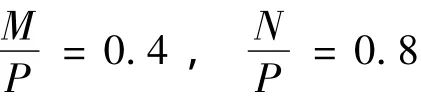
设X、Y、Z分别代表俯仰振动、垂向振动和俯仰角最大值，由于本文的优化目标是希望这三个值均能降低，即求函数T的最小值，其表达式为:

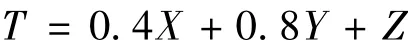
将iSIGHT中2500次优化计算的全部结果导入MATLAB中进行数据处理，第2195次计算结果为最优值，从图14、图15可以看出2 195次与初始点的对比。

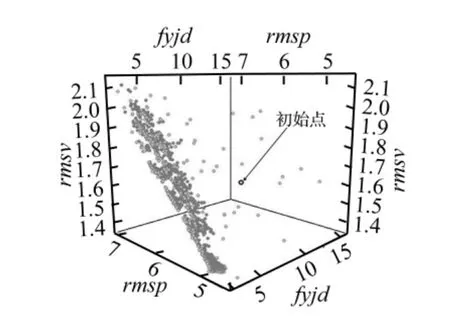
图13 计算散点图Fig.13 Optimization 3D scatter plot

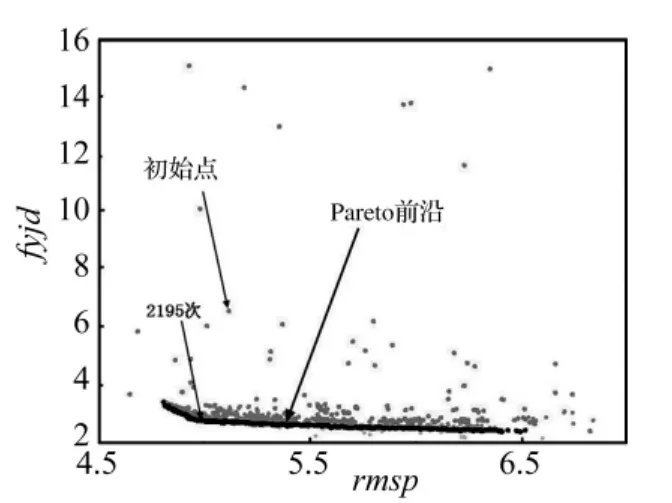
图14 rmsp-fyjd平面投影Fig.14 The rmsp-fyjd plane projection

将图13的计算散点图向两个坐标平面投影形成的Pareto前沿是两条近似直线，实际上在空间坐标系中Pareto前沿应该是一个前沿面，在MATLAB中的数据处理即是找出平面T=0.4X+0.8Y+Z与Pareto前沿面的切点，前沿面上的切点即为最优值点。

3.2 优化前后悬架性能比较

优化前后悬架特性参数如表3所示;优化前后的动挠度均方根值对比如表4所示，优化后的前后悬动挠度略有增大;优化前后的制动俯仰角最大值fyjd、俯仰振动与垂向振动加速度均方根值rmsp、rmsv如表5所示，从表中可以看出，加速制动工况下的俯仰角最大值优化效果最为明显，降低幅度高达57.7%，同时平顺性工况下的俯仰和垂向振动均有不同程度下降，完全实现了预期的优化目标。

表3 优化前后悬架特性参数对比Tab.3 Suspension parameters before and after optimization

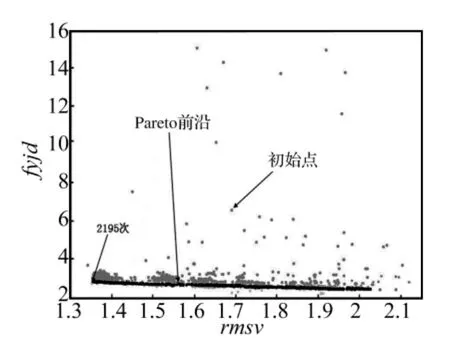
图15 rmsv-fyjd平面投影Fig.15 The rmsv-fyjd plane projection

表4优化前后动挠度均方根值对比Tab.4 Suspension dynamic deflection RMS values before and after optimization

表5 优化前后悬架性能对比Tab.5 Comparison of optimization objectives

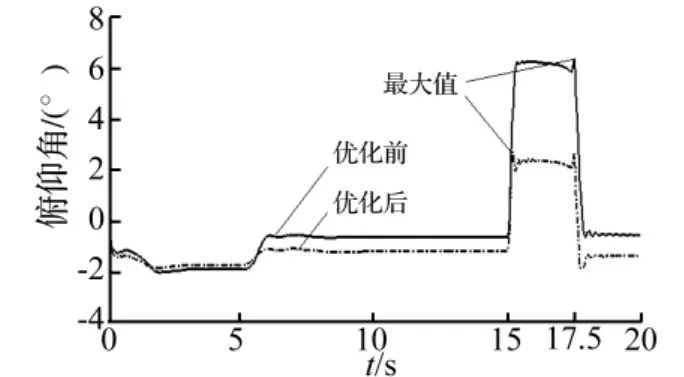
图16 优化前后的俯仰角变化Fig.16 Pitch angle before and after optimization

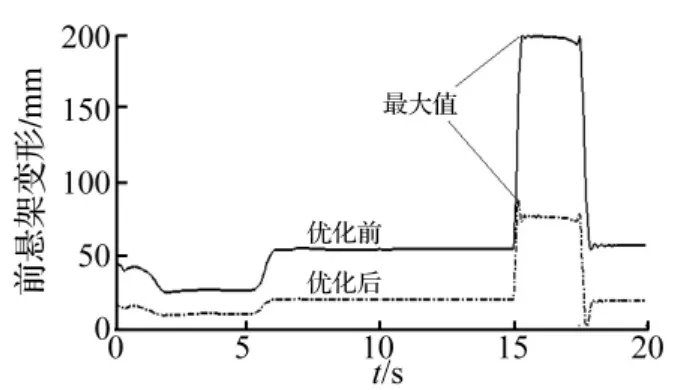
图17 优化前后前悬架变形Fig.17 Front suspension deformation before and after optimization

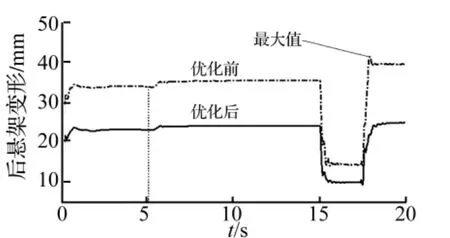
图18 优化前后的后悬架变形Fig.18 Rear suspension deformation before and after optimization

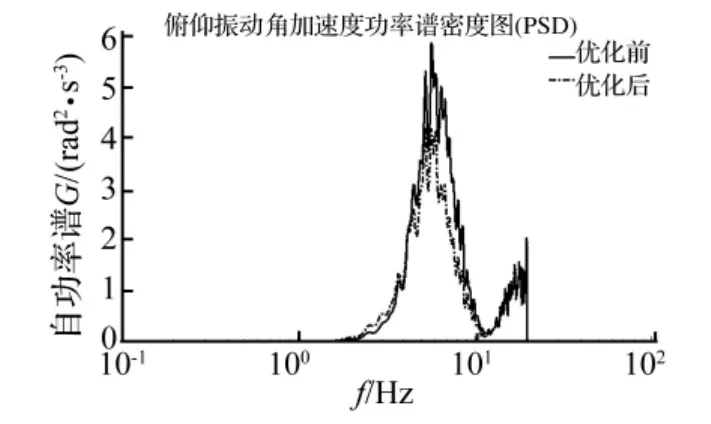
图19 优化前后俯仰振动对比Fig.19 Comparison of pitching vibration

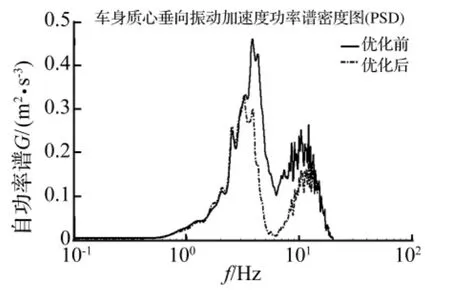
图20 优化前后车身质心垂向振动对比Fig.20 Comparison of vertical vibration

图16、17是优化以后加速/制动工况下的车身俯仰角的变化以及前悬架变形关系图，从图中可以看出俯仰角和悬架变形量明显降低了，优化后前悬架变形最大值降低为88 mm，叉管行程为105 mm，因此前悬架撞击限位的现象消除，骑乘舒适性得到了提高。图18是优化前后的后悬架变形图，从图中可以看出优化后的后悬架变形比优化前有相应的增大，优化后的悬架变形在前5 s的加速阶段和匀速阶段无明显突变，最大值41 mm出现在制动停止后的回弹阶段，小于后悬架的限位行程50 mm，因此在加速阶段和停止后的回弹阶段都不会引起后悬架的撞击。图19、20是优化前后俯仰振动和垂向振动的功率谱对比，从图中可以看出采用匹配后的悬架参数整车的俯仰和垂向振动均有降低，在整个频率范围内都没有出现恶化的现象，并且在低频范围内垂向振动降低的效果更加明显，优化后的整车性能满足了预期的要求。

通过以上优化前后两种工况下的悬架各项性能的对比分析，加速/制动工况的俯仰角峰值明显降低，骑乘舒适性得到改善，随机路面工况下的平顺性得到了提高，验证了多工况并行任务优化方法的有效性。

4 结论

(1)采用摩托车动力学专用软件BikeSim建立了路面和人－车系统模型，进行了加速制动工况和平顺性工况的仿真;以降低加速/制动工况下的俯仰角最大值、等速B级路面工况下的俯仰和垂向振动为目标，采用iSIGHT集成BikeSim和MATLAB的联合优化仿真的方法建立了两种工况的并行优化任务，对摩托车悬架系统进行了多目标优化，得到了Pareto前沿，实现了预期的优化目标。

(2)采用先优化后决策的模式，根据优化计算结果对Pareto前沿进行了分析，提出了一种确定目标权重的方法，找出了该权重下的最优值;通过对优化前后的俯仰角、前悬架变形、俯仰和垂向振动加速度均方根值、功率谱密度的结果分析表明，消除了制动时的前悬架撞击现象，骑乘舒适性得到了提高，同时随机路面平顺性得到了改善，验证了该方法的有效性，为车辆综合性能的优化提供了重要参考。

［1］李德宽.汽车工程手册摩托车篇［M］.北京:人民交通出版社，2001.

［2］Cossalter V，Doria A，Pegoraro R，et al.On the non-linear behavior of motorcycle shock absorbers［J］.Journal of Automobile Engineering，2010，224(1):15 －27.

［3］Audenino A L，Belingardi G.Modelling the dynamic behavior ofa motorcycle damper［J］. JournalofAutomobile Engineering，1995，209(4):249 －262.

［4］徐中明，卢少波，文 俐，等.基于MATLAB的摩托车舒适性仿真分析［J］.计算机仿真，2006，23(7):249－252.XU Zhong-ming，LU Shao-bo，WEN Li，et al.Simulation of ride comfort for motorcycle based on MATLAB［J］.Computer Simulation，2006，23(7):249 －252.

［5］陈 松，蹇开林，黄泽好，等.摩托车平顺性的仿真研究［J］.机械强度，2006，28(3):465 －469.

CHEN Song， JIAN Kai-Lin， HUANG Ze-hao， etal.Simulation and research of motorcycle's rider comfort［J］.Journal of Mechanical Strength，2006，28(3):465 －469.

［6］Spelta C，Savaresi S M，Fabbri L.Experiment analysis of a motorcycle semi-active rear suspension［J］. Control Engineering Pratice，2010，18(11):1239 －1250.

［7］ Wu L，Zhang W J.Hierarchical modeling of semi-active control of a full motorcycle suspension with six degrees of freedoms［J］. International Journal of Automotive Technology，2010，11(1):27 －32.

［8］吴 龙，陈花玲，陈玲莉.摩托车半主动悬架分层预测控制及仿真［J］.系统仿真学报，2006，18(8):2239 －2243.

WU Long，CHEN Hua-ling，CHEN Ling-li.Hierarchical preview control and simulation of semi-cative motorcycle suspension［J］.Journal of System Simulation，2006，18(8):2239－2243.

［9］于学华，丁康.汽车俯仰与跳动复合运动的分析［J］.噪声与振动控制，2005，4:26 －29.

YU Xue-hua，DING Kang.Analysis of the pitching and bouncing motion of the car［J］.Noise and Vibration Control，2005，4:26 －29.

［10］张永林.用谐波叠加法重构随机道路不平顺高程的时域模型［J］.农业工程学报，2003，19(6):32 －34.

ZHANG Yong-lin.Time domain model of road irregularities simulated using the harmony superposition method［J］.Transactions of The Chinese Society of Agricultural Engineering，2003，19(6):32 －34.

［11］张志飞，徐中明，贺岩松.基于多体动力学的摩托车平顺性分析［J］.中国机械工程，2010，21(8):988 －992.

ZHANG Zhi-fei，XU Zhong-ming，HE Yan-song.Analysis of motorcycle riding comfort based on multi-body dynamics［J］.China Mechanical Engineering，2010，21(8):988 －992.

［12］奉铜明，钟志华，闫晓磊，等.基于NSGA－Ⅱ算法的多连杆悬架多目标优化［J］.汽车工程，2010，32(12):1063－1066.

FENG Tong-ming，ZHONG Zhi-hua，YAN Xiao-lei，et al.Multi-objective optimization for multi-link suspension based on NSGA-Algorithm［J］.Automotive Engineering，2010，32(12):1063－1066.

［13］王 涛.汽车悬架参数的多目标多标准决策优化［J］.农业机械学报，2009，40(4):27 －32.

WANG Tao.Multi-objective and multi-criteriadecision optimization ofautomobile suspension parameters［J］.Transactions of the Chinese Society for Agricultural Machinery，2009，40(4):27 －32.

［14］王 涛，陶 薇.考虑随机因素的汽车悬架参数多目标稳健优化［J］.振动与冲击，2009，28(11):146 －149.

WANG Tao，TAO Wei.Multi-objective robust optimization of automobile suspension parameters considering random factors［J］.Journal of Vibration and Shock，2009，28(11):146－149.