主动转向系统鲁棒控制的研究

季鹏凯，沈 斌，陈 慧，章 桐

(1.同济大学机械工程学院，上海 200092;2.同济大学中德学院，上海 200092;3.同济大学新能源汽车工程中心，上海 201804)

前言

主动转向系统是可靠性与灵活性的有效结合，为汽车转向性能的提升提供了更大的发展空间。主动转向系统是在保持转向系统机械连接的基础上集成了变传动比机构而引入一个叠加转向转角到转向系统中，通过此叠加的转向角可以对转向过程进行主动干预，同时在主动转向控制系统失效时还可通过机械连接实现转向功能。主动转向控制策略是实现其性能的基础之一，现代最优鲁棒控制技术在主动转向系统的应用获得了广泛研究［1-3］，它考虑了车辆模型的各种不确定性、外界的各种干扰和传感器噪声等因素，来实现系统的鲁棒稳定性和鲁棒性能。主动转向系统对整车动力学特性将产生一定的影响，会减小整车的转向刚性，并产生柔性转向。针对模型参数不确定性，按H∞标准算法设计的控制器往往过于保守，而采用μ综合的方法可降低控制器的保守性，更容易获得相对精确的控制器。本文中将主动转向系统与2自由度整车模型集成，对模型参数不确定性进行了分析，采用了H∞标准算法、环路成形和μ综合的方法分别设计了最优鲁棒控制器。针对此3种控制器分别进行了μ分析和非线性仿真分析，并进行比较。

1 系统模型分析

1.1 整车模型

在近似恒定车速的平面运动情况下，2自由度整车模型可很好地体现整车在转向过程中的动力学特性。平面运动的2自由度整车模型结构如图1所示。忽略转向系统动力学特性、悬挂动力学特性、空气阻力和前轮转角Ackerman几何约束等的影响，车辆恒速行驶，汽车只做平面运动，整车可以简化成2自由度的非线性模型，即y轴方向的移动和绕z轴的横摆运动。

整车模型［1，3］可表达为

轮胎侧偏角［3-4］可表示为

式中:γ为横摆率，β为整车侧偏角，m为整车质量，I为整车z轴转动惯量，lf和lr分别为质心距前、后轴的距离，v为质心车速，fw为侧风干扰，δs为前轮转角，αi和fyi(i=f，r分别表示前轮和后轮)分别为轮胎侧偏角和横向力。前、后轮胎的侧向力采用Pacejka的“魔术公式”计算［4］:

式中 bi，ci，di和 ei(i=f，r)分别为刚性因子、形状因子、峰值因子和曲率因子，其参数决定于轮胎特性、路面状况和车辆操纵状态等因素。设路面摩擦因数为1，轮胎模型的各参数的数值如表1。

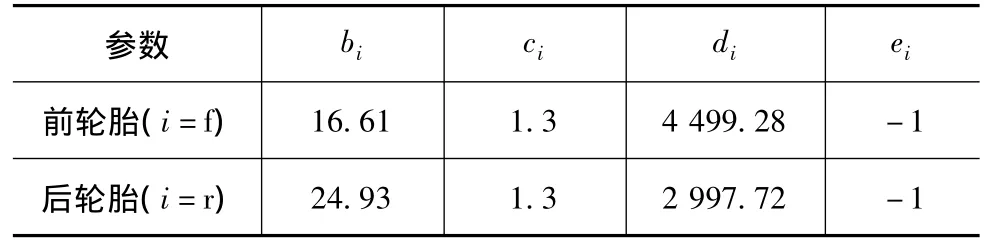
表1 轮胎模型参数

在小侧偏角假设的情况下进行如下的线性近似处理:

式中Kf和Kr分别为前、后轮的侧偏刚度。则可以得出忽略侧风干扰的线性2自由度整车模型为

1.2 主动转向系统模型

主动转向系统中动力学模型如图2所示。图中，Th、δc和 Jc分别为转向盘转矩、转向盘位置和转向盘转动惯量，Tm1、δm1和 Jm1分别为主动转向控制电机转子的输出转矩、位置和转动惯量，Ts、δs和 Js分别为转向机和轮胎等集中质量转换到前轮主轴销的转矩、位置和转动惯量，Bc和 kc为管柱的阻尼和刚度系数，Bm1和km1为主动转向控制电机的阻尼和刚度系数，δp为小齿轮的位置，im为主动转向电机转子到小齿轮的传动比，ic为转向盘到小齿轮的传动比，is为小齿轮到轮胎主轴销的传动比，ζ为轮胎拖距。

忽略各转动惯量与阻尼的影响，根据主动转向系统的结构可以列出如下方程组［5］:

从而得出转向车轮转角 δs与 δc，δm1，β 和 γ 的关系式:

1.3 引入主动转向系统、模型参数不确定性和侧向干扰的整车模型

转向系统模型的动力学特性对整车动力学特性会产生较大的影响，所以主动转向系统的模型应该集成到整车模型中，同时考虑侧风等侧向力的干扰，定义:x=［β，γ］T，υ =［δc，fw，δm1］，则

因为ρ总是小于1，由上述方程中可以看出，主动转向系统的引入使得前轮侧偏刚度变得偏小，使整车动力学特性更加偏向不足转向特性，适当的不足转向可提高转向过程的安全性，但过度的不足转向特性会使车辆驾驶变得困难，增加驾驶者微调节的负担。

考虑到汽车速度信号可以通过传感器和观测器精确获得，所以本文中仅考虑前、后轮胎的侧偏刚度的不确定性和整车转动惯量的不确定性，同时注意到ρ和Kf总是同时出现，设定不确定性参数如下:

其中，p1，p2和 p3反映了各参数 ρKf，Kr和 I与名义参数和偏离的百分比。定义辅助信号:

其中:Δ =diag(δ1，δ2，δ3)

可以得到如下具有不确定性的整车模型:

其中:u=δm1;ω =［δc，fw］T;yu=γ

2 鲁棒控制器的设计

2.1 系统广义模型分析与加权函数设计

主动转向控制系统的开环结构如图3所示。图中:yd为期望的横摆速率;yn为带有量测干扰(Noise)的整车模型横摆速率响应;yu为整车模型的响应输出;ey和eu分别代表对性能和控制量的评价指标;Gr为参考模型;Gv为整车模型;Wp、Wu和Wn分别为性能加权函数、控制量加权函数和量测噪声加权函数。

Gr定义为一阶传递函数［2］:

式中isd为期望转向传动比。

鲁棒控制器的设计在一定程度上取决于各加权函数的选择。Wp和Wu体现各变量的频率特性和指标间的相对重要性。Wp-1约束了闭环系统灵敏度函数的频响幅值范围，对闭环系统与理想模型的跟踪误差范围和外界干扰对系统输出的影响程度进行了限制，一般要求在低频范围内获得较高的跟随精度，在高频部分考虑高频量测干扰等的影响而降低跟随精度的限制。Wu用于限制控制作用的最大输出量，确保高频时的控制能量消耗低和低频时的控制精度高。Wn定义为高通滤波器，用于模拟传感器的噪声频域模型，并体现传感器在不同频率时的量测精确程度。各加权函数定义如下:

将转向盘的输入看做是扰动，将开环系统结构表示为Gop，集成鲁棒控制器 C和不确定性模块的闭环系统结构表示为图4。

2.2 控制器的设计

设计目标是求解有理控制器C使增广被控对象Gop内部稳定，且输入w到输出z的传递函数‖LFTL(LFTU(Gop，Δ)，C)‖∞＜1，LFTL和 LFTU分别表示下分式变换和上分式变换。考虑结构不确定性，为了同时获得鲁棒稳定性和鲁棒性能，采用μ综合方法进行鲁棒控制器设计［6］。μ综合方法是基于结构奇异值的迭代算法，分别交替保持D和K不变，逐次迭代求解，每次计算使式(16)的左侧减小。

式中DΔ为一对角阵集合，其中的任意元素D满足D·Δ=Δ·D，DΔ可定义为

迭代过程中首先预设对角常数缩放矩阵D的初值(例如单位矩阵)，然后固定D通过求解标准H∞最优问题求解C:

然后固定所求得的C，在选定的频率范围内通过求解凸最优问题，即求解D:

并通过曲线拟合D(jω)获得D(s)，此D(s)可用于下次求解C的迭代中，重复上述过程反复进行迭代计算，直到终止条件达到，来求得鲁棒控制器。

车辆参数见表2，基于表2中的参数，采用μ综合方法经过9次D-K迭代计算可以获得一个23阶控制器Cmu，最大结构奇异值为0.97。

基于相同的权函数，采用标准H∞算法，即通过求解Riccati方程的设计方法可获得一个7阶鲁棒控制器Cinf，其H∞范数为0.33。

另外还可以采用H∞环路成形的设计方法进行鲁棒控制器设计［1］，H∞环路成形方法不采用上述的加权函数，而是采用前、后补偿器，即W1和W2，分别设为

表2 车辆参数

可获得一个最大稳定边界为0.4的4阶鲁棒控制器 Clsp。

控制器的阶次代表控制器动力学模型的内部状态数量，控制器的输出可看作是各状态的加权和，所以控制器的阶次越高越容易实现对复杂对象的控制，越容易获得高的综合性能指标，但高阶次控制器同时也会带来实施的困难、高成本和可靠性降低等不利因素。在确保控制效果的前提下忽略模型的次要部分可实现对控制器动力学模型的降阶。

2.3 控制器降阶处理

μ综合分析方法获得的控制器Cmu的阶次一般较高，为便于实际工程应用，须对获得的控制器进行降阶处理［7］。将控制器模型平衡处理后，采用Hankel范数近似方法实现降阶处理，获得10阶的降阶控制器Cmrd如下:

2.4 控制器对比分析

各控制器的频响曲线如图5所示。由图可见:全阶(23阶)控制器与降阶(10阶)控制器的bode图直到104rad/s的频率范围，两者的曲线都很接近，表明由各控制器实现的闭环系统将具有相近的性能;Clsp的低频增益最大，Cmrd与Cinf的低频相位响应相近，而Clsp的低频相位滞后最大。

图6为结构奇异值(μ)分析结果。由图可见:虽然在给定的参数范围内，3个控制器都可以保证常规稳定性和性能指标，但Cinf不能完全确保鲁棒稳定性和鲁棒性能，Clsp可确保鲁棒稳定性但不能确保鲁棒性能，Cmrd的鲁棒性能指标在低频部分不很理想，但在此频段的整体范围内可同时确保鲁棒稳定性和鲁棒性能。

3 非线性仿真

计算机系统仿真实施框图如图7所示，其中P为非线性整车模型。仿真时间均为5s。仿真中增加了最大横摆率限制功能，设置参数 Yawlmt为0.35rad/s，以便当参考模型输出的横摆率超出车辆稳定限值时对汽车转向进行限制，实现主动安全，Yawlmt可以看做是对Gr模型的扩展。

双移线仿真结果如图8所示，因为3个控制器的响应性能比较相近，所以图中仅给出采用控制器Cmrd的结果曲线。由图可见:非线性整车模型横摆率响应很好地跟随参考模型Gr的期望响应输出，从而可以控制转向系统对整车动力学特性的影响，并可以获得期望的整车动力学特性和期望的转向传动比。例如随速动态调整isd，在高速时提高转向传动比来提高驾驶稳定性，在低速时降低转向传动比来提高操纵灵活性。

侧风干扰仿真结果如图9所示，假设在1～2s时间区间突然受到4kN的侧风干扰，并假设驾驶人员没有对此干扰进行响应，并分别采用3种控制器进行仿真。由图可见:各鲁棒控制器都能有效抑制横摆率的波动，使整车基本保持原行驶航向;控制器Cmrd的稳态误差最大，超调量最小，另两个控制器的表现则相反，这与图6的鲁棒性能曲线表现相一致。

转向盘转角阶跃输入仿真结果如图10所示，假设转向盘在0.5s时阶跃输入1.5rad转角，并分别采用3种控制器进行仿真。由图可见:采用3个控制器的各主动转向系统都可自动弥补转向系统的柔性转向，提高转向灵敏度，也可在横摆率最大限值的情况下，抑制转向灵敏度，提高整车稳定性和主动安全性;控制器Cinf表现出较快的响应速度，超调量最大和稳态精度略差，控制器Clsp和Cmrd具有较好的稳态精度，3种控制器对横摆率的控制或抑制，和行驶轨迹的影响具有相近的效果。由图10(c)可见:对最大横摆率的限制使行驶轨迹产生一定偏离，所以最大横摆率限值的设定应在合理范围内，以降低对汽车目标行驶轨迹的影响。

4 结论

在2自由度线性整车模型的基础上集成了主动转向系统模型，并考虑了前、后轮侧偏刚度和整车转动惯量的不确定性，建立了线性和非线性整车系统模型。通过标准求解Riccati方程、环路成形和μ综合等方法分别设计了最(或次)优鲁棒控制器，对Cmu进行了降阶处理，对各控制器进行了鲁棒稳定性和鲁棒性能分析。基于非线性整车模型采用3种鲁棒控制器进行了系统仿真。μ分析结果表明，Cinf不能完全确保鲁棒稳定性和鲁棒性能，Clsp可确保鲁棒稳定性但不能确保鲁棒性能，虽然Cmrd的鲁棒性能指标在低频部分不很理想，但在此频段的整体范围内可同时确保鲁棒稳定性和鲁棒性能。尤其考虑结构不确定性，Cmrd更容易获得较小的保守性和整体较高的控制精度。非线性仿真结果表明，3种鲁棒控制器都能较好抑制模型参数不确定性、侧向干扰和量测噪声干扰，并能降低主动转向系统对整车动力学特性的影响，获得期望的转向传动比，有利于提高整车的灵活性、稳定性和主动安全性。

［1］ Mammar S，Koenig D.Vehicle Handling Improvement by Active Steering［J］.Vehicle System Dynamics，2002，3(38).

［2］ Yin Guodong，Chen Nan，Li Pu.Improving Handling Stability Performance of Four-Wheel Steering Vehicle via μ-Synthesis Robust Control［J］.Vehicular Technology，IEEE Transactions，2007，56(5):2432-2439.

［3］ Bilin Aksun Güvenç，Tilman Bünte，Dirk Odenthal，et al.Robust Two Degree-of-Freedom Vehicle Steering Controller Design［J］.IEEE Transactions on Systems Technology，2004，12(4):627-636.

［4］ Pacejka H B，Bakker E，Lidner L.A New Tire Model with an Application in Vehicle Dynamics Studies［C］.SAE Paper 890087.

［5］ Shen Bin，Ji Pengkai.The Analysis and Modeling of Active Front Steering System［C］.CCIE-Proc.:IEEE Int.Conf.Computing，Control and.Eng.Wuhan，China，2011.

［6］ Doyle，J，Packard A，Zhou K.Review of LFTS，LMIs，and μ［C］.Proceedings of the 30th IEEE CDC，Brighton:1227-1260，1991.

［7］ Samar R，Postlethwaite I，Gu D-W.Model Reduction with Balanced Realizations［J］.International Journal of Control，1995，62:33-64.