基于传感器信号重构的汽车主动悬架主动容错控制*

杨柳青，陈无畏

(1.合肥工业大学机械与汽车工程学院，合肥 230009;2.安徽交通职业技术学院汽车与机械工程系，合肥 230051)

前言

汽车主动悬架系统(active suspension system，ASS)由汽车悬架、传感器、控制器和作动器组成。目前，建立在各元器件完好无故障基础上的主动悬架控制研究能明显改善被动悬架系统(passive suspension system，PSS)性能［1-3］。但由于元器件使用时间延长和老化等原因，会导致系统中传感器或作动器出现故障，造成按完好情况设计的控制器误控制，达不到预期控制效果，甚至使控制效果部分或全部丧失，影响汽车乘坐舒适性。而容错控制(fault tolerant control，FTC)在系统部件发生故障时仍能维持系统性能或将性能维持在可接受范围内。

文献［4］和文献［5］中基于作动器和传感器完好分别对半车悬架和整车悬架进行输出反馈H∞控制。文献［6］和文献［7］中针对作动器故障利用观测器进行故障诊断，通过控制器重构设计研究汽车悬架容错控制。文献［8］中针对汽车液压主动悬架传感器故障基于滑模控制技术在容错控制器的设计方面作了些尝试。但对于不改变主动悬架控制器结构，而通过传感器信号重构方法对汽车主动悬架故障进行主动容错控制，尚鲜有文献涉及。

据此，本文中采用主动悬架7自由度整车模型，充分考虑传感器常见的增益变化、恒偏差、卡死和输出饱和等故障，建立故障悬架(fault active suspension system，FASS)模型。运用线性矩阵不等式(LMI)法设计基于自适应技术的观测器和故障估计系统。通过估计传感器故障和重构故障传感器信号，实现汽车主动悬架主动容错控制。在主动悬架采用输出反馈H∞控制基础上，对车身垂向加速度传感器出现的多种故障情况于Matlab/Simulink环境中进行故障估计与容错控制的仿真，并对仿真结果进行分析。

1 系统建模

1.1 主动悬架7自由度整车模型

考虑车身垂向、俯仰、侧倾运动和前后非簧载质量垂向运动，建立主动悬架7自由度整车动力学模型［9-10］，如图1 所示。

车身垂向、俯仰、侧倾运动方程分别为

式中:ms为车身质量;xs为车身质心垂向位移;F1、F2、F3、F4分别为车身左前、右前、左后、右后悬挂点的受力;Ip为车身俯仰转动惯量;θ为俯仰角;a、b分别为车身质心到前、后轴距离;Ir为车身侧倾转动惯量;φ为侧倾角;d为前后轴轮距。

非簧载质量垂向运动方程为

式中:mui为非簧载质量;xui为非簧载质量垂向位移;kti为轮胎刚度;xgi为路面垂向高度变化量;ci为阻尼系数;ki为悬架刚度;xsi为车身悬挂点垂向位移;ui为作动器控制输出力;下标 i取1，2，3，4，分别代表车身左前、右前、左后、右后悬挂点位置。

路面输入运动方程采用滤波白噪声模型［11］，即

式中:wi是均值为零高斯白噪声输入;v为车速;G0为路面不平度系数;f0为下截止频率;下标i取1，2，3，4，分别代表左前、右前、左后、右后轮胎位置。

式中:A为14×14维矩阵;B1为14×4维矩阵;B2为14×4维矩阵;C为11×14维矩阵;Cy为3×14维矩阵;D1为11×4维矩阵;D2为11×4维矩阵;Dy为3×4维矩阵。

1.2 故障悬架模型

汽车主动悬架量测输出利用车身垂向加速度、俯仰角速度和侧倾角速度传感器实现测量。常见传感器故障行为有卡死、增益变化和恒偏差3种［12］。当第j个传感器发生此类故障时，对应量测输出为

式中:yj、yjf分别为第j个传感器完好输出和故障输出;Δj为反映第j个传感器增益变化故障程度大小的故障增益;αj为第j个传感器卡死位置或恒偏差值。j=1，2，3分别代表车身垂向加速度、俯仰角速度和侧倾角速度传感器。

当 Δj∈(0，1)，αj=0 时，表示传感器发生增益变化故障;当Δj=1，αj≠0时，表示传感器发生恒偏差为 αj故障;当 Δj=0，αj≠0时，表示传感器在 yjf=αj处发生卡死故障(其中传感器输出为零的卡死情况本文暂不作考虑);特殊情况是当αj为传感器测量值最大或最小值时，为传感器发生输出饱和故障。传感器发生上述故障时主动悬架系统故障输出为

故障悬架状态空间模型为

2 汽车主动悬架控制

对主动悬架7自由度整车系统模型Gm采用加权输出反馈H∞控制［4］，控制框图如图2所示。

设计的加权输出反馈H∞控制器U=K(s)Y具有如下状态空间实现:

3 容错控制策略

基于传感器信号重构的汽车主动悬架主动容错控制策略框图如图3所示。汽车主动悬架输出反馈控制器以量测输出传感器信号作为输入，当量测输出传感器发生相应故障时，传感器故障输出将偏离完好输出，发生异常变化，进而导致控制器控制输出信号异常，最终影响汽车主动悬架目标控制效果。通过基于自适应技术设计的观测器获得汽车主动悬架系统输出残差r，再利用以输出残差为信号设计的悬架故障估计系统，估计出量测输出传感器故障信号，利用故障传感器故障估计值和故障输出共同重构量测输出传感器信号，以重构的量测输出传感器信号作为输出反馈控制器的输入，实现汽车故障悬架主动容错控制目标，使故障悬架性能恢复到与完好无故障悬架性能相接近的水平。

4 传感器信号重构容错控制设计

4.1 基于自适应观测器故障估计

汽车主动悬架量测输出传感器发生相应故障时，设计如下自适应观测器［14-15］来获得主动悬架状态和传感器故障估计信息:

式中:Ks为学习率，是维数适当待设计矩阵。取状态误差e=-X，输出残差r=-Y，故障误差ef=-f。从而有

取Lyapunov函数V=ψTP1ψ，将V求导后代入式(24)得

将悬架干扰输入w视为扰动输入，参照文献［15］的方法，引入H∞性能指标:

以保证性能指标J＜V(0)且Lyapunov函数稳定。由式(27)有

取 PG=N，QKs=M，有

找到适当的P、Q、N、M矩阵使以上线性矩阵不等式组成立，则满足性能指标J＜V(0)且Lyapunov函数稳定。在Matlab中用feasp命令求式(29)线性矩阵不等式组可行解P*、Q*、N*、M*。自适应观测器增益矩阵G、故障估计律学习率Ks分别为

4.2 传感器信号重构与容错控制

汽车主动悬架系统量测输出传感器发生相应故障时，利用式(21)获得传感器故障估计值，结合传感器故障输出，将故障悬架量测输出传感器信号重构为［16］

式中Yr为故障悬架量测输出传感器的重构信号。

故障悬架传感器信号重构后，进一步将重构信号Yr作为输出反馈控制器的输入，实现故障悬架主动容错控制。这种基于输出传感器信号重构的主动容错控制无须改变汽车主动悬架输出反馈控制器的结构和参数，仍采用原控制律，利用传感器重构信号Yr进行容错控制。控制输入为

5 仿真结果与分析

汽车主动悬架模型参数值如表1所示［17］。汽车以15m/s速度驶过B级路面，路面不平度系数为64×10-6m3，下截止频率为0.1Hz。选取干扰输入加权系数阵 Sw=diag(0.000 14，0.000 14，0.000 14，0.000 14)，控制输出加权传递函数阵Wz=diag(1，1，1，1，1，1，1，1，W2，W1，W1)，控制输出加权系数阵Sz=diag(25，25，25，25，0.022，0.022，0.022，0.022，6，5，5)。其中，W1、W2分别为旋转方向和垂直方向加权传递函数［4］:

式中s为拉普拉斯算子。

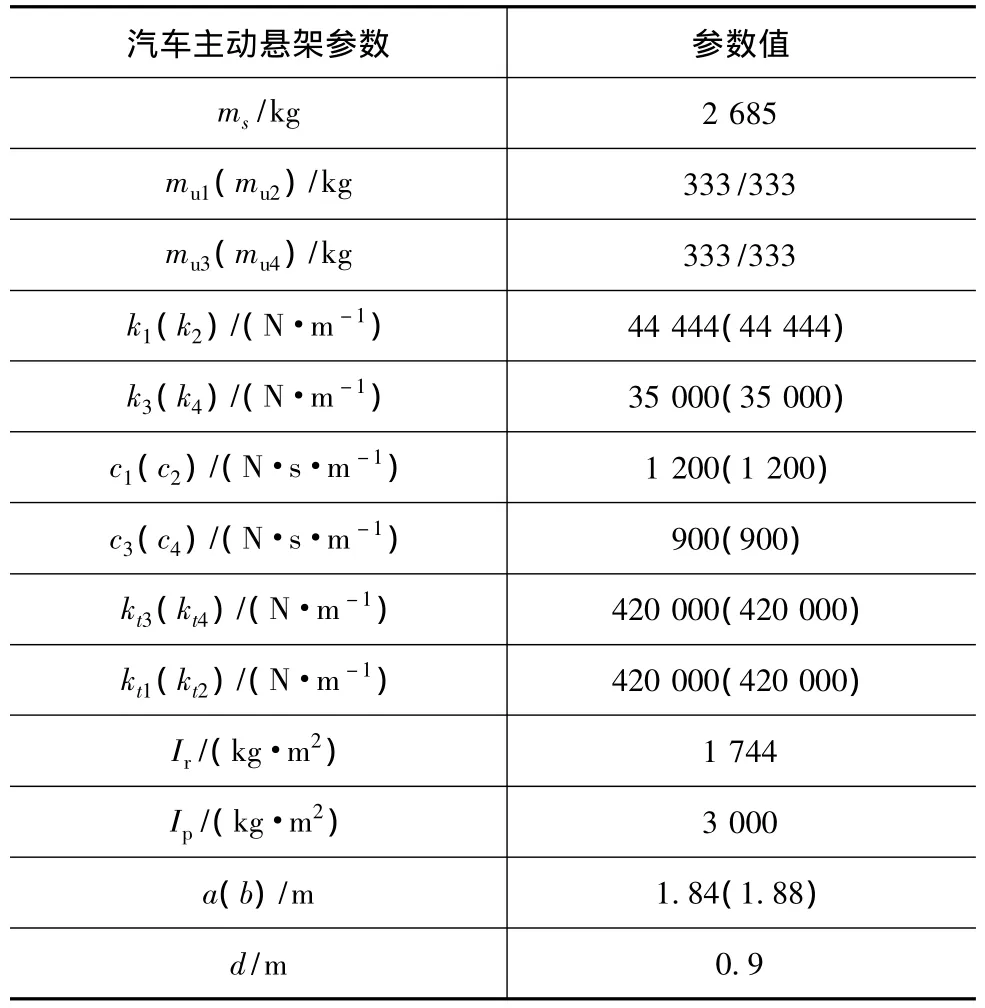
表1 汽车主动悬架模型参数值

在Matlab/Simulink中实现良好的汽车主动悬架控制。

5.1 故障估计结果与分析

取H∞性能指数γ=0.015，利用LMI求得自适应观测器增益矩阵G和自适应故障估计律学习率Ks。在Matlab/Simulink中分别建立主动悬架系统、输出反馈H∞控制器、自适应观测器、故障估计系统、传感器故障和传感器信号重构等仿真模块，构建汽车主动悬架传感器信号重构容错控制系统。在仿真时仅考虑单个传感器故障，并以车身垂向加速度传感器为故障对象，故障1～4具体情况描述见表2。为清晰对比容错控制前后结果，在仿真中设置了容错控制时刻tr值。

表2 故障具体情况描述

车身垂向加速度传感器在完好无故障时完好输出y1与故障1～4情况下故障输出y1f及故障实际值f1与故障估计值fe1仿真结果对比分别见图4、图5、图6和图7。

由图4可见:在故障时刻tf=1s前，车身垂向加速度传感器完好无故障，其故障输出y1f与完好无故障状态时完好输出y1相同，自适应观测器和故障估计系统能较为准确地估计出该传感器状态，故障估计值为0;故障时刻tf=1s后，车身垂向加速度传感器处于故障1情况，此时传感器故障输出y1f相对传感器完好输出损失80%;自适应观测器和故障估计系统能较为准确地估计出传感器完好输出和故障输出间的差值，即故障估计值，且故障估计误差数值很小，仅为10-3数量级，即故障估计值与故障实际值基本吻合;在容错时刻tr=5s，故障悬架系统采取输出传感器信号重构容错控制后，自适应观测器和故障估计系统仍能很好地跟踪故障信号，对输出故障值作出较为准确的故障估计。

由图5可见:在车身垂向加速度传感器发生故障(时刻tf=1s)前，自适应观测器和故障估计系统较为准确地估计出故障估计值为0;在故障时刻tf=1s后和容错时刻tr=2s后，自适应观测器和故障估计系统均能较为准确地估计出传感器完好输出和故障输出间的故障值，故障估计误差数值很小，也仅为10-3数量级，故障估计值与故障实际值基本一致。

同样由图6和图7可以看出，车身垂向加速度传感器处于故障3或故障4情况前后和容错控制后，自适应观测器和故障估计系统均能很好跟踪故障信号，能较为准确地估计故障值，故障估计值与故障实际值基本一致。

以上仿真结果表明，当车身垂向加速度传感器出现增益变化、恒偏差、卡死和输出饱和等故障时，基于自适应技术设计的观测器和故障估计系统能较为准确地估计出量测输出传感器故障实际值，且故障估计误差的数量级很小。

5.2 容错控制结果与分析

车身垂向加速度、俯仰角速度和侧倾角速度传感器发生相应故障后，在故障估计基础上按照式(32)和式(33)对量测输出进行传感器信号重构，仍以表2中所列故障情况分别对故障悬架进行容错控制仿真。

当车身垂向加速度传感器分别处于故障1～4情况时，容错控制下的故障悬架各性能响应与完好无故障汽车主动悬架性能响应对比见图8～图11。

由图8可见:故障时刻tf=1s起，车身垂向加速度传感器处于故障1状态，故障悬架车身垂向加速度、俯仰角和左前悬动挠度响应开始变差，振幅明显变大，其峰值分别增加31.2%、40.4%和24.3%，均方根值分别增加38.1%、40.0%和22.7%;但自主动容错控制时刻tr=5s起，基于传感器信号重构对故障悬架采取主动容错控制，故障悬架上述性能水平经0.5～1s短暂时滞后开始逐渐恢复，最终恢复至与完好无故障主动悬架性能相接近的水平。

由图9可见:故障时刻tf=1s起，车身垂向加速度传感器发生恒偏差故障，处于故障2状态，其中故障悬架俯仰角受影响最显著，振幅呈现逐渐增大趋势，左前悬架动挠度振幅亦明显增大，其峰值增加24.3%，均方根值增加73.1%;但自主动容错控制时刻tr=2s起，在容错控制策略下，上述性能响应也在经4～5.5s的时滞后开始逐渐恢复，最终恢复至与完好无故障主动悬架性能相接近的水平。

同样，由图10和图11可见:车身垂向加速度传感器分别处于故障3或故障4状态，主动容错控制前各性能响应均变差，均方根值与峰值均增大;而在主动容错控制时刻tr=2s后故障悬架性能响应经短暂时滞后逐渐恢复至与完好无故障主动悬架性能相接近的水平。

以上容错控制仿真结果表明，基于量测输出传感器信号重构的主动容错控制策略使故障悬架性能经短暂时滞后得到很好的恢复，提高了主动悬架系统控制的可靠性和控制品质。

6 结论

(1)采用输出反馈控制的汽车主动悬架在传感器故障影响下，会使车辆乘坐舒适性变差。视路面输入为干扰输入和给定H∞性能指标约束情况下，基于自适应技术的观测器设计和故障估计系统设计可转化成LMI可行解问题。

(2)基于传感器故障估计值和故障输出采取的传感器信号重构，因其它完好无故障传感器故障估计值为0，在重构过程中与完好无故障传感器完好输出直接叠加，故无须对故障传感器部位进行隔离确认。

(3)全面考虑传感器常见增益变化、恒偏差、卡死和输出饱和等故障，基于自适应技术的故障估计系统能很好地跟踪传感器故障信号，较为准确地估计量测传感器故障值，且故障估计误差很小，仅为10-3～10-5数量级。

(4)基于传感器故障估计值和故障输出可实现量测输出传感器信号重构，且利用传感器重构信号可实现汽车故障悬架主动容错控制。当传感器发生常见故障情况时，在基于传感器信号重构的主动容错控制策略下，故障悬架经0.5～5.5s时滞后其各项性能可逐渐恢复至与完好无故障汽车主动悬架性能相接近的水平，该策略可改善故障悬架的控制效果，提高其控制可靠性和控制品质。

［1］ Yoshimura T，Teramura I.Active Suspension Control of a Onewheel Car Model Using Single Input Rule Modules Fuzzy Reasoning and a Disturbance Observer［J］.Journal of Zhejiang University Science，2005，6A(4):251-256.

［2］ Campos J，Davis L，Lewis F L，et al.Active Suspension Control of Ground Vehicle Heave and Pitch Motion［C］.Proceedings ofthe 7th Mediterranean Conference on Control and Automation，Haifa，Israel，1999:222-233.

［3］ Zheng Ling，Li Yi Nong，Chen Bing Kui.A New Semi-active Suspension Control Strategy Through Mixed H2/H∞Robust Technique［J］.Journal of Central South University of Technology(Enlish E-dition)，2010，17(2):332-339.

［4］ 方敏，汪洪波，陈无畏.汽车主动悬架系统H∞控制器的降阶［J］.控制理论与应用，2007，24(4):553-560.

［5］ Chen Hong，Guo Kong Hui.Constrained H∞Control of Active Suspensions:An LMI Approach［J］.IEEE Transactions on Control Systems Techology，2005，13(3):412-421.

［6］ Yetendje Alain，Seron Maria，De Dona Jose.Diagnosis and Actuator Fault Tolerant Control in Vehicle Active Suspension［C］.Third International Conference on Information and Automation for Sustainability，Melbourne，2007:153-158.

［7］ Gaspar Peter，Szabo Zoltan，Bokor Jozsef.The Design of a Reconfigurable Suspension Control System Based on an FDI Filter［C］.16th Mediterranean Conferenceon Controland Automation，France，2008:446-450.

［8］ Chamseddine Abbas，Noura Hassan.Control and Sensor Fault Tolerance of Vehicle Active Suspension［J］.IEEE Transactions on Control Systems Techology，2008，16(3):416-433.

［9］ Crolla D A，喻凡.车辆动力学及其控制［M］.北京:人民交通出版社，2003.

［10］ Ikenaga S，Lewis F L，Campos J，et al.Active Suspension Control of Ground Vehicle Based on a Full-vehicle Model［C］.Proceedings of the American Control Conference，Chicago，2000:4019-4024.

［11］ Yu Fan，Crolla D A.An Optimal Self-tuning Controller for an Active Suspension［J］.Vehical System Dynamics，1998，29(1):51-65.

［12］ 闻新，张洪钺，周露.控制系统的故障诊断与容错控制［M］.北京:机械工业出版社，1998.

［13］ 俞立.鲁棒控制——线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002.

［14］ 姜斌，冒泽慧，杨浩，等.控制系统的故障诊断与故障调节［M］.北京:国防工业出版社，2009.

［15］ 王占山，张化光.故障估计的自适应观测器设计［J］.东北大学学报(自然科学版)，2005，26(1):221-224.

［16］ Jiang Bin，Chowdhury Fahmida N.Fault Estimation and Accommodation for Linear MIMO Discrete-Time Systems［J］.IEEE Transactions on Control Systems Technology，2005，13(3):493-499.

［17］ 陈无畏，孙启启，胡延平，等.基于干扰抑制的汽车转向与悬架系统的集成控制［J］.机械工程学报，2007，43(11):98-104.