高职数学教材编写的思考与探索
2013-09-07肖业胜
肖业胜
(武汉工程职业技术学院 湖北 武汉:430080)
高职教育经过十多年的发展,无论是在办学规模,还是在招生规模上可比肩普通高等教育,为社会培养了大量的,遍布各行各业急需的技术人才。教材建设伴随高等职业教育的发展与改革也得到了快速发展,形形色色的教材应运而生,这些教材都在一定程度上体现了高职教育的特色。但在教学过程中,我们发现,有些教材太注重理论知识的系统、全面讲述,数学应用介绍不足,不能较好的体现数学知识服务于专业运用的导向作用;而有些教材则相反,完全基于面向应用的考虑,在教材中大量引入专业性较强的实例,忽略了学生专业知识尚不具备的现实,其结果是,讲授的东西学生难以接受,同时,数学必需的知识也得不到有效的讲解等。
1 高职教学教材编写应树立的观念
我们认为,高职高专教材的编写首先应在尊重数学知识体系的前提下,尽可能的降低理论要求,以“适度、够用”为准则;知识点的选取、衔接自然,不悖常理;重视培养学生分析问题,解决实际问题的能力,提高学生的综合能力和数学素养。数学不仅仅是一个“工具”,还承载着思维训练与素质提高的使命。
数学教材的行文尽量通俗易懂,避免抽象的表述,充分考虑教学对象的实际情况。对于较复杂的运算问题,可以借助数学工具软件辅助完成。内容的呈现“采用提出问题(引例)——数学知识讲解——知识应用介绍”的思路。
教学内容的编排采用模块化设计,设置基本模块和可选模块,便于在专业人才培养计划制定时,由专业教师针对专业特点选取必需的数学模块内容,最大化数学教学服务专业课教学的效用。
高职高专数学教学的任务是,为学生学习专业提供“必需”、“够用”的数学基础知识,提供学生在自己的职业生涯中可以继续学习所需的数学能力、数学素养和缜密的数学思维方式。通过高等数学的教学达到以下目标:让学生掌握微积分的基本理论与基本运算;掌握学习后续课程必需的数学基本知识;具有基本的运算能力和初步运用数学软件的能力;初步掌握数学建模思想,能运用数学知识解决简单的实际问题;初步形成以“数学方式”思考问题、解决问题的能力。
2 《高等应用教学》教材的编写实例剖析
基于上述考虑,在学院的大力支持下,我们组织编写了《高等应用数学》一书。按模块化设计的思想将内容划分为三个部分:基础篇、拓展篇和应用篇。其中基础篇内容包括:函数基础知识的回顾,极限与连续,导数与微分及其应用,一元函数积分及其应用问题;拓展篇内容包括:多元函数微积分,级数;应用篇内容包括:积分变换、矩阵代数和概率统计知识初步。
教材的主要特色体现在四个方面:
一是依据教育部制定的《高职高专高等数学课程教学基本要求》,贯彻“以应用为目的,以够用力度”的原则。在尽可能保持数学学科特点的基础上,注意到高职教育的特殊性,对教学内容进行了精选,淡化理论性和系统性。如,对两个重要极限,在极限部分以结论形式,不加证明的给出极限结果,要求学生能运用重要极限的结果解决相应问题的极限求法,而在洛必达法则部分则以例题的形式给出两个重要极限结果正确性的证明;又如,我们将微分方程的内容分割为两个部分,一阶微分方程问题作为不定积分的应用予以提出,并给出其解法,二阶微分方程问题则置于拉普拉斯变换的应用中讲授,并能解决非正弦电路中的一些应用问题。
二是书中概念的引入尽可能从实际背景入手,定理和结论一般只给出解释或简单的几何说明,例题的选取由易到难、循序渐进,力求通俗易懂,不要求十分复杂的计算和证明。如,分段函数的提出,我们引用了最新的累进税率计算方法:纳税问题
根据中华人民共和国个人所得税法(2012年)规定:公民的个人收入应依法缴纳个人所得税。所得税的计算办法为:在每个人的月收中,超过3500元以上的部分应该纳税,这部分收入称为应纳税所得额。就纳税所得额实行分段累积税率,按下表计算:

等级 全月应纳税所得额 税率/%1不超过3500元的部分0245超过3500元,不超过5000元 33超过5000元,不超过8000元 104超过8000元,不超过12500元 205超过12500元,不超过38500元 256超过38500元,不超过58500元 307超过58500元,不超过83500元 358超过83500元的部分
若某人的月工资收入为x元,列出他(她)应交纳的税款y与收入x之间的函数关系。
解(1)按纳税规定,当0≤x≤3500时,不必纳税,此时y=0;
(2)当3500<x≤5000时,纳税部分是x-3500,税率是3%,所以
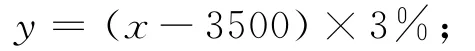
(3)当5000<x≤8000时,有3500元不必纳税,有1500元税率是3%,应纳税45元,再多出的部分是x-5000,税率是10%,所以
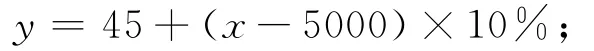
(4)依此类推,得到税款y与收入x之间的函数关系式:

=03500<x≤5000 y=(x-3500)×3%5000<x≤8000 y=(5000-3500)×3%+(x-5000)×10%=45+(x-5000)×10%8000<x≤12500y=(5000-3500)×3%+(8000-5000)×10%+(x-8000)×20%=45+300+(x-8000)×20%=345+(x-8000)×20%12500<x≤38500 y=345+(12500-8000)×20%+(x-12500)×25%=1245+(x-12500)×25%38500<x≤58500 y=1245+(38500-12500)×25%+(x-38500)×30%=7745+(x-38500)×30%58500<x≤83500 y=7745+(58500-38500)×30%+(x-58500)×35%=13745+(x-58500)×35%X>83500 y=13745+(83500-58500)×35%+(x-835000)×45%=22495+(x-835000)×45%应纳税款0≤x≤3500 y月收入
又如,第二个重要极限,我们由连续复利的计算问题提出:连续复利问题
现有一笔贷款A0(称本金),以年利率r贷出。若以一年为1期计算利息,1年末的本利和为A1=A|-0(1+r),2年末的本利和为A2=A1(1+r)=A0(1+r)2,…,t年末的本利和为At=A0(1+r)t。这是一年计息1期,t年末的本利和At的复利公式。若仍以年利率为r,一年不是计息1期,而是一年计息n期,且以为每期的利率来计算,在这种情况下,t年末的本利和为,这是一年计息n期,t年末的本利和At的复利公式。
上述计息期是有确定的时间间隔的,且一年计息次数有限。若计息期的时间间隔无限缩短,即计息次数n→∞,称这种情况为连续复利。
按连续复利计算的本利和为:

At=A0ert就是本金为A0,年利率为r,按连续复利计算,t年末的本利和计算公式。如本金10000元,年利率3.25%,5年期末按复利计算的本利和为10000(1+3.25%)5=11734.11,按连续复利计算的本利和为11764.5元。
再如,微积分基本定理给出了定积分计算的基本公式,我们通过一个物理中的【引例】质点的速度与位移引出:
已知一作变速直线运动的质点,其速度v(t)与位移s(t)的关系为s′(t)=v(t),那么,在时间间隔[a,b]内,质点的位移为
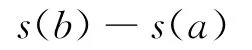
而另一方面,质点的位移又可以由定积分表示为
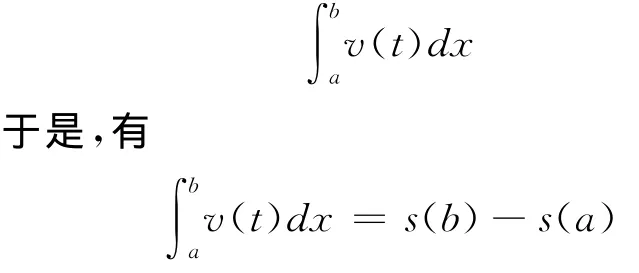
因为s′(t)=v(t)表明,s(t)是v(t)的原函数,所以,上式告诉我们,定积分∫bav(t)dx的值等于被积函数v(t)的原函数s(t)在积分上限的值减积分下限的值。
一般地,我们有微积分基本定理:若F(x)是连续函数f(x)在[a,b]上的一个原函数,则=F(b)-F(a)。
三是突出数学知识与专业知识的衔接,让数学的知识,思维的方式向专业领域迁移、渗透与发散,提升学生将实际问题转化为数学模型的能力;教材中的应用问题,都是数学知识向不同方面或专业领域渗透的问题,如,导数,在经济问题中是边际,在工程问题中是变化率;函数的相对变化率用于经济分析中的需求价格函数就是需求价格的弹性;工业生产,经营活动中的各种数据表都是代数中的矩阵;产品质量的某项指标我们总是假设其服从正态分布等。
四是将数学软件Mathematica的运用融入数学教学内容的各个部分。书中各知识点的计算和图示部分均以“注”的形式附Mathematica求解的命令,章后附Mathematica的基本运用知识,数学实验,并安排有上机操作练习,以巩固和加深Mathematica在解决数学问题中的应用,使学生能掌握运用计算工具解决复杂问题的计算,锻炼学生利用计算机求解数学问题的能力。数学软件的使用方法,不是数学课必讲内容,它仅作为教学辅助而存在,用法由学生自由获取。
分模块组织教材,将数学教学内容的选择权交给专业课教师,然后,根据所选内容合理的配置教学时数,这一方面能较好的应对课时减少的实际状况;另一方面,可以根据不同专业岗位对数学知识的需求,选取最适用的内容进行教学;三是解决了过去在教材选用中版本过多,过杂的问题,便于课程教学效果的考核检验。学生的数学能力不仅仅表现在掌握数学知识的多少,更在于是否具备运用数学知识,借助计算工具解决实际问题的能力。
[1]王华祖.浅析影响高职教材优化建设的因素及改进措施[J].出版发行研究,2011,(11):73-75.
[2]刘康声,戚文革.高职教材建设思路及创新[J].职业技术教育,2009,(8):54-56.
[3]王平安.职业教育课程政策研究[M].南京:南京大学出版社,2011.
[4]于润伟.高职高专教材的质量评价[J].职业技术教育,2007(23):20+35.
